Las corrientes de Foucault (II)
Modelo simple que calcula la fuerza de frenado
Sea una pieza metálica larga y ancha y de pequeño espesor que se mueve con velocidad constante v. Un campo magnético uniforme perpendicular al plano de la hoja metálica se aplica a una pequeña porción rectangular de dimensiones a y b.
Se supondrá que el campo magnético producido por las corrientes inducidas es suficientemente pequeño, para considerar que la fuerza de frenado proviene únicamente de la acción del campo magnético externo sobre las corrientes inducidas. Esto se produce si la velocidad v de la pieza metálica es inferior a una velocidad característica vc, que depende de la conductividad del metal y del espesor de la pieza.
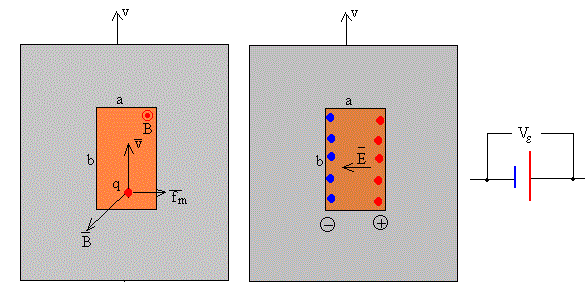
Supongamos que el campo magnético es perpendicular al plano de la hoja metálica, al moverse la pieza metálica con velocidad v, los portadores de carga q existentes en la pequeña región rectangular de dimensiones a y b experimentan una fuerza , tal como se muestra en la figura. Los portadores de carga son impulsados por la fuerza magnética hacia la derecha.
La separación de cargas produce un campo eléctrico , dirigido hacia la izquierda. Tenemos el equivalente a una batería cuya fem es igual a la diferencia de potencial Vε =vBa medida en circuito abierto.
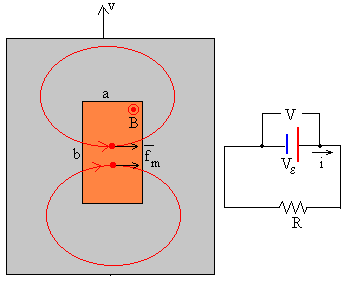
La pequeña región rectangular no está aislada del resto de la hoja metálica, que proporciona la conexión entre los dos terminales de la imaginaria batería por el que circula una corriente de intensidad i. El resto de la pieza metálica opone una resistencia R al paso de la corriente eléctrica. Mientras que la pequeña región rectangular presenta una resistencia interna r que calculamos aplicando la ley de Ohm.
siendo δ el espesor de la pieza metálica y σ la conductividad del metal. La ecuación del circuito se escribe i(r+R)=Vε
El cálculo de la resistencia R de la pieza metálica excepto la región rectangular es muy complicado.
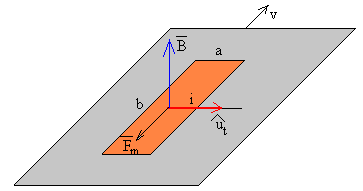
La fuerza que ejerce el campo magnético sobre esta porción de corriente rectilínea es
Se supone que la intensidad está uniformemente distribuida en la sección bδ
La fuerza se opone a la velocidad v de la pieza metálica y es proporcional a su velocidad, y al cuadrado del campo magnético B. El producto δab es el volumen de la porción de la pieza metálica que está bajo la influencia del campo magnético uniforme .
La energía disipada en la unidad de tiempo, es el producto de la fuerza por la velocidad, Fm·v, es proporcional al cuadrado del producto de la intensidad del campo magnético por la velocidad.
Deducción alternativa
De la ley de Ohm y de la fuerza de Lorentz, calculamos la densidad de corriente
-
El campo magnético tiene la dirección del eje Z,
-
La velocidad tiene la dirección del eje Y,
-
El campo eléctrico inducido , siendo V la diferencia de potencial entre los extremos de la región rectangular de anchura a.
-
El producto vectorial
Si es uniforme en la sección bδ, la intensidad i de la corriente que fluye por la región rectangular es
El primer término es la fem inducida Vε=vBa, el término que multiplica la intensidad es la resistencia r que presenta la región rectangular al paso de la corriente.
V es la diferencia de potencial en los terminales de la batería, y es también la diferencia de potencial entre los extremos de la resistencia R, por lo que V=iR. Llegamos a la ecuación del circuito vBa=i(r+R)
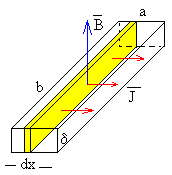
Expresamos la fuerza que ejerce el campo magnético sobre la corriente de intensidad i, en términos del vector densidad de corriente cuyo módulo es la intensidad dividido el área J=i/(bδ), y cuya dirección y sentido es el del vector unitario .
El elemento de volumen dV=bδ·dx, señalado en color amarillo en la figura
Obtenemos el mismo resultado
Corrientes de Foucault en una pieza metálica de forma cilíndrica
Ya hemos estudiado el problema de la corriente inducida que se genera en una espira situada en una región en la que el campo magnético varía con el tiempo.
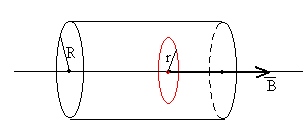
Consideremos un cilindro conductor de radio R colocado en un campo magnético paralelo al eje X, que varía con el tiempo de acuerdo con la ecuación
Bx=B0sin(ω t)
Por simetría, las corrientes inducidas tendrán la forma de circunferencias centradas en el eje X
El flujo a través de una de estas líneas será (el vector campo y el vector superficie son paralelos)
Φ =Bx·π r2
La fem inducida en la línea de corriente de radio r es
Esta fem es la que pone en movimiento a los portadores de carga contenidos el volumen de la capa cilíndrica de longitud L comprendida entre r y r+dr. Originando una intensidad
i=Vε/Re
Siendo Re la resistencia del tubo (no confundirla con el radio R del cilindro) de longitud 2π r y de sección Ldr por el que circulan las cargas.
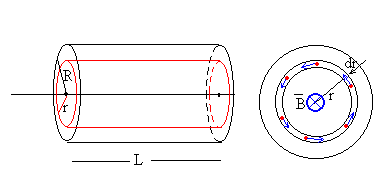
La fórmula de la resistencia (resistividad por longitud del conductor y dividido por su sección) se expresa
donde ρ es la resistividad del material. Por tanto, la intensidad es
La energía por unidad de tiempo (potencia) disipada es Vε·di, y para calcular la potencia total se integra entre 0 y R (radio del cilindro)
Teniendo en cuenta que el valor medio durante un periodo 2π /ω de la función periódica coseno cuadrado es1/2.
La potencia disipada es proporcional al cuadrado de la frecuencia ω del campo magnético variable. Esta es la razón por la que los hornos de inducción utilizan frecuencias elevadas.
En esta deducción se ha despreciando el campo magnético creado por las propias corrientes de Foucault. Esta aproximación no es válida para materiales de resistividad nula (materiales superconductores).
En los transformadores no podemos cambiar la frecuencia, ni la resistividad del material empleado como núcleo (se emplea un determinado tipo de material). Para reducir la pérdidas se actúa sobre la geometría de las líneas de corriente, se tratará de reducir sus dimensiones (fijarse que la potencia disipada <P> es proporcional a la cuarta potencia del radio del cilindro).
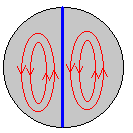
Si al cilindro de radio R, se le divide por la mitad mediante una pared aislante que pase por el eje, las pérdidas se reducen notablemente. Las líneas de corriente tienen ahora la forma que se muestra en la figura. El cálculo de la potencia disipada en esta configuración es ya muy complicado.
Se debe hacer notar que si el cilindro se corta por un plano aislante perpendicular al eje, la potencia disipada no cambia.
Referencias
Del modelo de fuerza de frenado
Wiederick H. D. Gauthier D. A., Rochon P. Magnetic braking: Simple theory and experiment. Am. J. Phys. 55 (6) June 1986, pp. 500-503.

