El dispositivo formado por un globo y un disco CD, que se describe en el artículo citado en las referencias, es fácil de construir, recomendable para demostraciones de aula, ferias de la ciencia o acontecimientos similares.

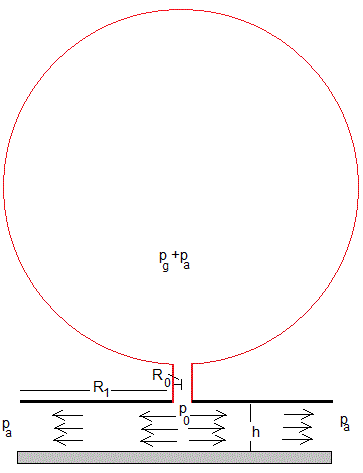
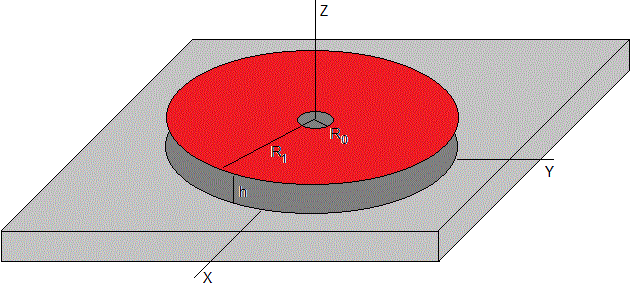
Un globo lleno de aire a presión p_a+p_g, siendo p_a la presión atmosférica, se conecta al orificio de un disco de radio R₁. El aire que sale por el orificio hace que el disco se mantenga suspendido sobre el plano horizontal a una altura h.

En el dispositivo experimental, la presión del globo es de p_g=0.01·p_a≈1000 Pa. El volumen se calcula a partir de la medida del diámetro del globo. El tiempo que tarda el globo en desincharse es de alrededor de 15 s. El flujo de aire Q=0.3·10^-3 m³/s

El radio del orificio central del disco es R₀=6 mm y el radio exterior R₁=60 mm. El disco se mantiene suspendido paralelo a la superficie horizontal a una altura medida de h=0.55 mm.

Supondremos que el aire se comporta como un fluido incompresible, en régimen laminar de viscosidad η

El perfil de la velocidad de un fluido que se mueve en régimen laminar entre dos placas fijas, se obtiene aplicando La ecuación de Navier-Stokes para un fluido incompresible bajo la acción de un gradiente de presión es

${\displaystyle \eta \frac{d^{2}v}{d{z}^2}=\frac{dp}{dr}}$

Donde v es la velocidad en la dirección radial, y dp/dr es el gradiente de presión

Integramos dos veces respecto de z

${\displaystyle \begin{array}{l}\frac{dv}{dz}=\frac{1}{\eta }\frac{dp}{dr}z+c_1\hfill \\ v(z)=\frac{1}{2\eta }\frac{dp}{dr}{z}^2+c_{1}z+c_2\hfill \end{array}}$

Las constantes c₁ y c₂ se calculan, sabiendo que para z=0 y para z=h, v=0

${\displaystyle \begin{array}{l}\begin{array}{l}{c}_2=0\\ c_1=-\frac{1}{2\eta }\frac{dp}{dr}h\end{array}\hfill \\ v(z)=\frac{1}{2\eta }\frac{dp}{dr}z\left(z-h\right)\hfill \end{array}}$

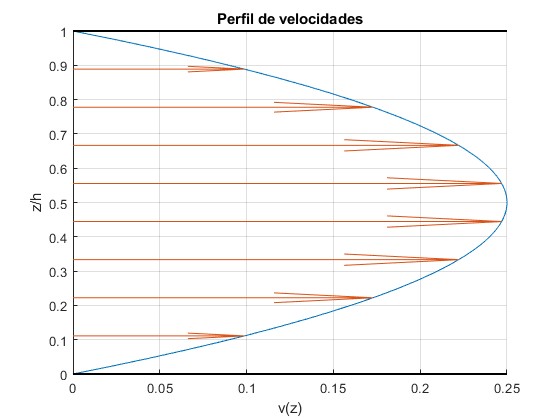
Representamos el perfil de la velocidad del aire que se mueve entre el disco y el plano horizontal, en función de z/h

h=1;
hold on
fplot(@(z) -z.*(z-h),[0,h])
zz=linspace(0,h,10);
quiver(zz,zeros(1,length(zz)), zeros(1,length(zz)), -zz.*(zz-h),0)
line([0,0],[0,0.25],'lineWidth',1.5,'color','k')
line([1,1],[0,0.25],'lineWidth',1.5,'color','k')
hold off
grid on
xlabel('z/h')
ylabel('v(z)')
title('Perfil de velocidades')
view(90,-90)

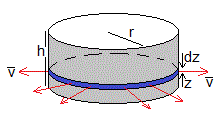
Calculamos el volumen de fluido que atraviesa cualquier sección en la unidad de tiempo

${\displaystyle Q={\displaystyle \underset{0}{\overset{h}{\int }}v(z)\left(2\pi r·dz\right)}}$

A medida que el radio aumenta, la velocidad media del aire dismunuye en proporción inversa. Q=2πrh<v>

El flujo es

${\displaystyle Q=\frac{\pi r}{\eta }\frac{dp}{dr}{\displaystyle \underset{0}{\overset{h}{\int }}\left(z^2-hz\right)dz}=\frac{\pi r}{\eta }\frac{dp}{dr}\left(\frac{h^3}{3}-\frac{h^3}{2}\right)=-\frac{\pi r}{6\eta }\frac{dp}{dr}{h}^3}$

Despejamos el gradiente de presión dp/dr e integramos, sabiendo que la presión atmosférica p_a se alcanza cuando r=R₁ en el bode del disco. La presión a la distancia r del centro del disco es mayor

${\displaystyle \begin{array}{l}\frac{dp}{dr}=-\frac{6\eta Q}{\pi h^3}\frac{1}{r}\\ {\displaystyle \underset{p_a}{\overset{p}{\int }}dp}=-\frac{6\eta Q}{\pi h^3}{\displaystyle \underset{R_1}{\overset{r}{\int }}\frac{dr}{r}}\\ p(r)-p_a=-\frac{6\eta Q}{\pi h^3}\ln \left(\frac{r}{R_1}\right)\\ \Delta p(r)=\frac{6\eta Q}{\pi h^3}\ln \left(\frac{R_1}{r}\right)\end{array}}$

La presión en el centro del disco es igaul a la presión en r=R₀

${\displaystyle \Delta p(R_0)=\frac{6\eta Q}{\pi h^3}\ln \left(\frac{R_1}{R_0}\right)}$

Representamos Δp(r) en función de r

Los datos son

• Viscosidad, η=1.85·10^-5 kg/(m·s)
• Flujo de aire, Q=0.3·10^-3 m³/s
• Radio del orificio, R₀=6 mm
• Radio del disco, R₁=60 mm
• Altura de equilibrio, medida, h=0.55 mm

k=6*1.856e-5*0.3e-3/(pi*0.55e-3^3);
f=@(r) k*log(60./r);
fplot(f,[6,60])
line([0,6],[f(6),f(6)])
grid on
xlabel('r (mm)')
ylabel('\Deltap (Pa)')
title('Presión')

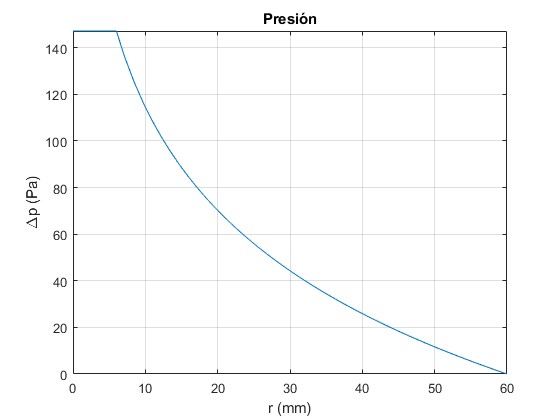
Sabiendo que la presión atmosférica p_a=1.013·10⁵ Pa, la presión debida al chorro de aire Δp(r) es muy pequeña comparada con la presión atmosférica

Fuerza sobre el disco

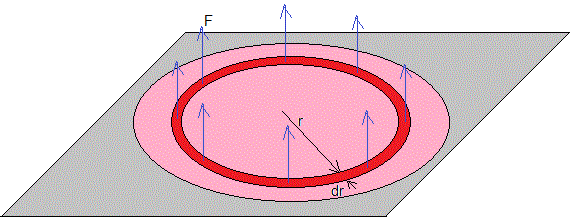
La fuerza sobre el disco debida a la diferencia de presión

${\displaystyle \begin{array}{l}F={\displaystyle \underset{R_0}{\overset{R_1}{\int }}\Delta p(r)\left(2\pi r·dr\right)}+\Delta p(R_0)\pi R_0^2=\frac{12\eta Q}{h^3}{\displaystyle \underset{R_0}{\overset{R_1}{\int }}r\ln \left(\frac{R_1}{r}\right)dr}+\frac{6\eta Q}{\pi h^3}\ln \left(\frac{R_1}{R_0}\right)\pi R_0^2=\\ \frac{6\eta Q}{h^3}\left\{2\ln \left(R_1\right){\displaystyle \underset{R_0}{\overset{R_1}{\int }}rdr}-2{\displaystyle \underset{R_0}{\overset{R_1}{\int }}r\ln rdr}+R_0^2\ln \left(\frac{R_1}{R_0}\right)\right\}\end{array}}$

Integramos por partes

${\displaystyle \begin{array}{l}{\displaystyle \int x\ln x·dx},\{\begin{array}{l}u=\ln x,du=\frac{dx}{x}\\ dv=x·dx,v=\frac{x^2}{2}\end{array}\\ \frac{x^2}{2}\ln x-\frac{1}{2}{\displaystyle \int x·dx=}\frac{x^2}{2}\ln x-\frac{x^2}{4}=\frac{x^2}{2}\left(\ln x-\frac{1}{2}\right)\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}F=\frac{6\eta Q}{h^3}\left\{\ln \left(R_1\right)\left(R_1^2-R_0^2\right)-R_1^2\left(\ln \left(R_1\right)-\frac{1}{2}\right)+R_0^2\left(\ln \left(R_0\right)-\frac{1}{2}\right)+R_0^2\ln \left(\frac{R_1}{R_0}\right)\right\}=\\ F=\frac{3\eta Q}{h^3}\left(R_1^2-R_0^2\right)\end{array}}$

En el equilibrio, la fuerza debida a la presión del aire F=mg es igual al peso. Se despeja la altura h del disco sobre el plano horizontal

${\displaystyle \begin{array}{l}mg=\frac{3\eta Q}{h^3}\left(R_1^2-R_0^2\right)\\ h={\left(\frac{3\eta Q}{mg}\left(R_1^2-R_0^2\right)\right)}^{1/3}\end{array}}$

Los datos son

• Masa del disco, m=21.45 g
• Viscosidad, η=1.85·10^-5 kg/(m·s)
• Flujo de aire, Q=0.3·10^-3 m³/s
• Radio del orificio, R₀=6 mm
• Radio del disco, R₁=60 mm

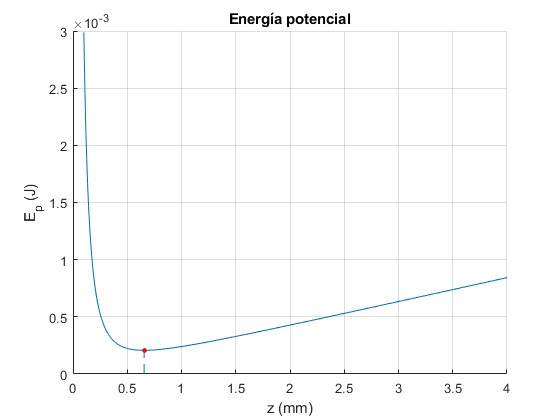
La altura de equlibrio, calculada es h=0.656 mm

Energías potenciales

La fuerza F debida a la presión es inversamenta proporcional al cubo de la altura z del disco sobre el plano horizontal, F=C/z³. La energía potencial E_p(z) correspondiente a esta fuerza es

${\displaystyle \begin{array}{l}{\displaystyle \underset{z}{\overset{\infty }{\int }}\frac{C}{z^3}dz}=E_p(z)-E_p(\infty )\\ \frac{C}{2z^2}=E_p(z)\end{array}}$

La energía potencial correspondiente al peso mg es mgz. La posición de equilibrio corresponde al mínimo de la suma de las dos energías potenciales

Representamos la función E_p(z) señalando el mínimo

${\displaystyle E_p(z)=\frac{3\eta Q\left(R_1^2-R_0^2\right)}{2z^2}+mgz}$

C=3*1.85e-5*0.3e-3*(60e-3^2-6e-3^2)/1e-6;
mg=21.45*9.8*1e-6;
f=@(z) mg*z+C./(2*z.^2);
hold on
fplot(f,[0.1,4])
h=(C/mg)^(1/3);
plot(h,f(h),'ro','markersize',3,'markerfacecolor','r')
line([h,h],[0,f(h)],'lineStyle','--')
hold off
grid on
xlabel('z (mm)')
ylabel('E_p (J)')
title('Energía potencial')

Referencias

Charles de Izarra, Grégoire de Izarra. Stokes equation in a toy CD hovercraft. Eur. J. Phys. 32 (2011) pp. 89–99