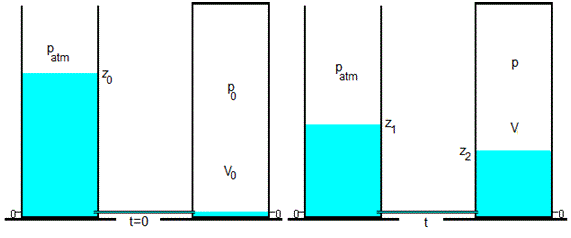
En la figura, se muestran los dos depósitos unidos por un tubo capilar de radio R y longitud L>>R. El líquido tiene densidad ρ y viscosidad η. En el instante t=0, el depósito de la izquierda está abierto a la atmósfera y está lleno hasta una altura z₁=z₀ y el de la derecha está cerrado, su volumen es V₀ y su presión es p₀<p_atm, la altura de líquido en este depósito es z₂=0.

En el instante t, el líquido pasa del depósito de la izquierda hacia el de la derecha a través del tubo capilar, la altura del líquido en el depósito de la izquierda ha descendido de z₀ a z₁, y en el depósito de la derecha ha ascendido de 0 a z₂, la presión del aire en el depósito cerrado es p y su volumen es V.

Vamos a determinar la presión p del aire en el depósito cerrado de la derecha en función del tiempo t. En la práctica de laboratorio, la presión del aire p(t) se mide con un manómetro y a partir de estos datos, obtenemos la medida de la viscosidad η del fluido

Tubo capilar

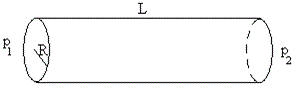
La ley de Poiseuille afirma que la cantidad de fluido de viscosidad η que atraviesa en la unidad de tiempo (gasto) la sección de un tubo de radio R y longitud L cuando está sometido a una diferencia de presión p₁-p₂ en sus extremos es

${\displaystyle G=\frac{\pi (p_1-p_2)R^4}{8L\eta }}$

Puesto que el movimiento del líquido en los dos recipientes es muy lento, podemos considerar que las presiones p₁ y p₂ en los extremos del tubo capilar son aproximadamente.

p₁=p_atm+ρgz₁
p₂=p+ρgz₂

debidas a las alturas de fluido z₁ y z₂ en los respectivos depósitos. p_atm es la presión atmosférica en el depósito de la izquierda y p es la presión del aire en el depósito de la derecha

La diferencia de presión es, Δp=p₁-p₂=(p_atm-p)+ρ(z₁-z₂).

Si los depósitos son pequeños y la cantidad de líquido que pasa de un depósito a otro ΔV=V₀-V es pequeña, podemos despreciar la presión correspondiente a la diferencia de alturas ρ(z₁-z₂). La diferencia de presión es aproximadamente Δp=p₁-p₂≈p_atm-p

El paso de fluido a través del capilar cesa cuando la presión p del depósito cerrado se aproxima a la presión atmosférica, p_atm, el líquido que ha pasado del recipiente abierto al cerrado será V_liq

Suponiendo que el aire se comporta como un gas ideal, p₀V₀=pV=p_atm(V₀-V_liq). p₀ es la presión inicial del aire del depósito cerrado y V₀, su volumen inicial cuando no contiene líquido

${\displaystyle V_{liq}=V_0\left(1-\frac{p_0}{p_{atm}}\right)}$

Presión del aire del recipiente cerrado

El gasto G es el volumen de líquido que pasa a través del tubo capilar en la unidad de tiempo. El volumen de líquido en el recipiente de la derecha crece y decrece el volumen V del aire en el recipiente

${\displaystyle \begin{array}{l}G=-\frac{dV}{dt}=-p_0{V}_0\frac{d}{dt}\left(\frac{1}{p}\right)=\frac{p_0{V}_0}{p^2}\frac{dp}{dt}\\ \frac{\pi (p_{atm}-p)R^4}{8L\eta }=\frac{p_0{V}_0}{p^2}\frac{dp}{dt}\\ \frac{dp}{dt}=\frac{\pi R^4}{8L\eta p_0{V}_0}{p}^2(p_{atm}-p)\end{array}}$

Definiendo las variables adimensionales

${\displaystyle \begin{array}{l}\rho =\frac{p}{p_{atm}}\tau =t\frac{\pi R^4{p}_{atm}^2}{8L\eta p_0{V}_0}\\ \frac{d\rho }{d\tau }={\rho }^2(1-\rho )\end{array}}$

No confundir la variable adimensional ρ con la densidad del líquido

Integramos, con la condición inicial de que en el instante t=0, o bien τ=0, la presión en el recipiente es p₀ o bien, ρ₀=p₀/p_atm

${\displaystyle \begin{array}{l}{\displaystyle \underset{{\rho }_0}{\overset{\rho }{\int }}\left(\frac{1}{{\rho }^2}+\frac{1}{\rho }+\frac{1}{1-\rho }\right)}d\rho ={\displaystyle \underset{0}{\overset{\tau }{\int }}d\tau }\\ -\frac{1}{\rho }+\ln \left(\frac{\rho }{1-\rho }\right)+\frac{1}{{\rho }_0}-\ln \left(\frac{{\rho }_0}{1-{\rho }_0}\right)=\tau \\ \frac{1}{\rho }+\ln \left(\frac{1}{\rho }-1\right)-\frac{1}{{\rho }_0}-\ln \left(\frac{1}{{\rho }_0}-1\right)=-\tau \\ \left(\frac{1}{\rho }-1\right)+\ln \left(\frac{1}{\rho }-1\right)-\left(\frac{1}{{\rho }_0}-1\right)-\ln \left(\frac{1}{{\rho }_0}-1\right)=-\tau \end{array}}$

Llamamos x=1/ρ-1

${\displaystyle \begin{array}{l}x+\ln x=-\tau +x_0+\ln x_0\\ \ln x=-x-\tau +x_0+\ln x_0\\ x=\exp \left(-x-\tau +x_0+\ln x_0\right)\\ x\exp (x)=x_0\exp \left(x_0-\tau \right)\\ x=W\left(x_0\exp \left(x_0-\tau \right)\right)\\ \rho =\frac{1}{1+W\left(x_0\exp \left(x_0-\tau \right)\right)}\end{array}}$

Véase Función W de Lambert. Como 0<ρ≤1, utilizaremos la rama W₀(x)

Casos límite:

• Cuando τ tiende a ∞ el argumento de W₀(x) tiende a cero y W(0)=0, por tanto, ρ tiende a 1. Es decir, la presión p del recipiente cerrado tiende a al presión atmosférica, p_atm
• Cuando τ=0, $W\left(x_0\exp \left(x_0\right)\right)=x_0$

Finalmente, la presión p en función del tiempo t es

${\displaystyle \begin{array}{l}p=\frac{p_{atm}}{1+W\left(x_0\exp \left(x_0-\beta t\right)\right)}\\ x_0=\frac{p_{atm}}{p_0}-1\beta =\frac{\pi R^4{p}_{atm}^2}{8L\eta p_0{V}_0}\end{array}}$

Ejemplo

El recipiente abierto tiene un volumen de 300 mL y se llena con 200 mL de líquido, el recipiente cerrado, V₀=280 mL. El capilar tiene una longitud de L=14.11 cm y un radio de R=0.5 mm. Se reduce la presión del recipiente cerrado mediante una jeringa a p₀=0.8 p_atm. Se abre la válvula que comunica los dos recipientes y el líquido de viscosidad desconocida empieza descender en el recipiente abierto y a ascender en el recipiente cerrado. Mediante un manómetro, se mide la presión p del aire en el recipiente cerrado.

Supongamos que el líquido es agua destilada cuya viscosidad es η=0.956·10^-3 Pa·s

R=0.5e-3; %radio del capilar
L=14.11/100; %longitud del capilar
V0=280e-6; %volumen del depósito cerrado
patm=1.013e5; %presión atmosférica
p0=0.8*patm; %presión inicial del aire en el depósito cerrado
eta=0.956e-3; %viscosidad del agua destilada
 
beta=pi*R^4*patm^2/(8*L*eta*p0*V0);
x0=patm/p0-1;
p_r=@(t) 1./(1+lambertw(0,x0*exp(x0-beta*t))); %p/patm
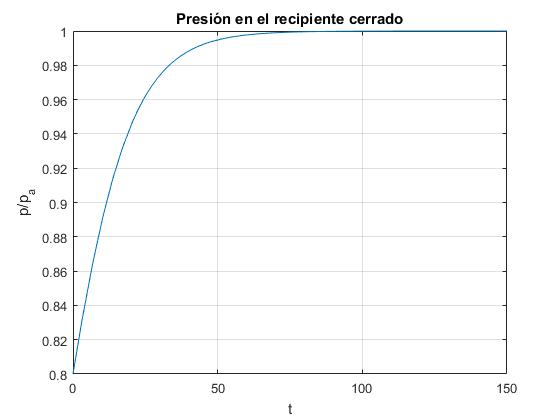
fplot(p_r,[0,150])
grid on
xlabel('x')
ylabel('p/p_a')
title('Presión en el recipiente cerrado')

Actividades

Se elige el líquido en el control titulado Líquido de viscosidades

Fuente: Manual de Física, Koshkin N. I. , Shirkévich M. G.. Editorial Mir (1975)

Se establece la presión inicial p₀ del aire en el recipiente cerrado, como una fracción d ela presión atmosférica, p_atm

Se pulsa el botón titulado Nuevo

Observamos como una parte de los 200 mL de líquido que hemos puesto en el recipiente abierto va pasando al recipiente cerrado cuyo volumen es V₀=280 mL. La presión p en este recipiente que mide el manómetro, va aumentado hasta que se aproxima a la presión atmosférica

Por ejemplo, cuando p₀=0.8p_atm. El líquido V_liq que pasa al recipiente cerrado es

${\displaystyle \begin{array}{l}{V}_{liq}=V_0\left(1-\frac{p_0}{p_{atm}}\right)\\ V_{liq}=280·(1-0.8)=56\text{mL}\end{array}}$

Referencias

Taha Massalha, Rafael M Digilov. Capillary viscometer with a pressure sensor: a subject for student projects. Eur. J. Phys. 36 (2015) 065045

La aplicación HTML5-canvas contiene la implementación de la función W de Lambert en javascript que se ha tomado de la página web https://github.com/protobi/lambertw. 2015 Pieter Sheth-Voss. Version 3, 29 June 2007