Al estudiar el concepto de viscosidad, vimos que la fuerza por unidad de área es proporcional al gradiente de velocidad, la constante de proporcionalidad se denomina viscosidad η

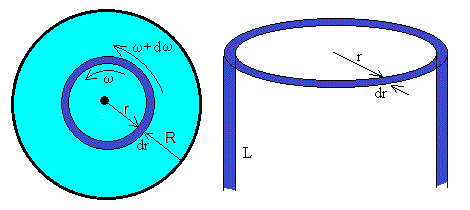
En este caso, la capa de fluido considerada es de forma cilíndrica de espesor dr. La velocidad angular ω varía con la distancia radial r. El gradiente de velocidad se expresa en coordenadas cilíndricas

${\displaystyle \frac{F}{A}=\eta r\frac{\partial \omega }{\partial r}}$

En el estado transitorio, la velocidad angular ω va a depender de dos variables r y t, A=2πr·L es el área lateral de la capa cilíndrica de radio r y longitud L.

Hay dos fuerzas que actúan sobre la porción de fluido contenido en la capa cilíndrica de radio interior r y exterior r+dr y altura L:

• F_r, que ejerce la porción de fluido en el interior del cilindro de radio r, sobre la superficie interior de la capa cilíndrica

• F_r+dr, que ejerce la porción de fluido del cilindro hueco de radio interior r+dr y el radio exterior R del recipiente, sobre la superficie exterior de la capa cilíndrica

Sus momentos respecto del eje de rotación son de signos contrarios

${\displaystyle \begin{array}{l}{F}_r=2\pi L\eta r^2{\frac{\partial \omega }{\partial r}|}_r\\ F_{r+dr}=2\pi L\eta {\left(r+dr\right)}^2{\frac{\partial \omega }{\partial r}|}_{r+dr}\end{array}}$

Aproximamos F_r+dr con los dos primeros términos del desarrollo, f(x+dx)≈f(x)+(df/dx)dx

${\displaystyle \begin{array}{l}{F}_{r+dr}\approx 2\pi L\eta \left(r^2+2rdr+d{r}^2\right)\left({\frac{\partial \omega }{\partial r}|}_r+{\frac{{\partial }^2\omega }{{\partial }^{2}r}|}_{r}dr\right)\approx \\ 2\pi L\eta \left\{\left(r^2+2rdr\right){\frac{\partial \omega }{\partial r}|}_r+r^2{\frac{{\partial }^2\omega }{{\partial }^{2}r}|}_{r}dr\right\}\end{array}}$

Se han despreciado los términos proporcionales a dr² y dr³

El momento producido por ambas fuerzas respecto del eje de rotación es

${\displaystyle \begin{array}{l}dM=F_{r+dr}(r+dr)-F_{r}r\approx \\ 2\pi L\eta \left\{\left(r^3+2r^{2}dr+r^{2}dr+\mathrm{...}\right){\frac{\partial \omega }{\partial r}|}_r+\left(r^3+\mathrm{...}\right){\frac{{\partial }^2\omega }{{\partial }^{2}r}|}_{r}dr-r^3{\frac{\partial \omega }{\partial r}|}_r\right\}\\ dM=2\pi L\eta r^2\left\{3\frac{\partial \omega }{\partial r}+r\frac{{\partial }^2\omega }{{\partial }^{2}r}\right\}dr\end{array}}$

Aplicamos la ecuación de la dinámica de rotación $dM=dI\frac{\partial \omega }{\partial t}$ a la capa cilíndica de radio interior r, radio exterior r+dr y longitud L. Primero, calculamos la masa dm y momento de inercia, dI=dm·r² de la capa respecto del eje de rotación.

${\displaystyle \begin{array}{l}dI=dm·r^2=\left(\rho 2\pi r·drL\right)r^2=\rho 2\pi r^{3}Ldr\\ dM=dI\frac{\partial \omega }{\partial t}\\ 2\pi L\eta r^2\left\{3\frac{\partial \omega }{\partial r}+r\frac{{\partial }^2\omega }{{\partial }^{2}r}\right\}dr=(\rho 2\pi r^{3}Ldr)\frac{\partial \omega }{\partial t}\\ \frac{3}{r}\frac{\partial \omega }{\partial r}+\frac{{\partial }^2\omega }{{\partial }^{2}r}=\frac{\rho }{\eta }\frac{\partial \omega }{\partial t}\end{array}}$

Resolveremos esta ecuación diferencial en derivadas parciales, con diferentes condiciones iniciales y de contorno

El estado estacionario

En el estado estacionario, la velocidad angular de rotación ω(r) de cada una de las capas cilíndricas de fluido es independiente del tiempo

${\displaystyle \begin{array}{l}\frac{3}{r}\frac{d\omega }{dr}+\frac{d^2\omega }{d^{2}r}=0\\ \frac{3}{r}z+\frac{dz}{dr}=0\end{array}}$

Llamando z=dω/dr, la integral es inmediata, lnz=-3lnr+c₁, donde c₁ es una constante de integración. Despejando, z=c₁/r³

Integramos de nuevo

${\displaystyle \begin{array}{l}\frac{d\omega }{dr}=\frac{c_1}{r^3}\\ \omega =c_2-\frac{c_1}{2r^2}\end{array}}$

Expresión que hemos obtenido en la página titulada, Fluido entre dos cilindros coaxiales

Se pone en marcha el recipiente cilíndico

Un recipiente cilíndrico contiene un fluido y están en reposo. Imaginemos que en el instante t=0, el recipiente cilíndrico se pone a girar con velocidad angular Ω y se mantiene con esta velocidad. Vamos a resolver la ecuación diferencial en derivadas parciales, con las siguientes condiciones:

• La condición de contorno es, ω(R,t)=Ω. La capa de fluido en contacto con el recipiente se mueve con velocidad angular constante Ω

• La condición inicial es ω(r,0)=0. Fluido en reposo

Procederemos a resolver esta ecuación diferencial siguiendo los mismos pasos que en la página titulada Conducción del calor en un cilindro muy largo

Definimos la función u(r,t)=ω(r,t)-ω(r,∞)=ω(r,t)-Ω. En términos de esta nueva función, la ecuación diferencial se escribe

${\displaystyle \frac{3}{r}\frac{\partial u}{\partial r}+\frac{{\partial }^{2}u}{{\partial }^{2}r}=\frac{\rho }{\eta }\frac{\partial u}{\partial t}}$

• La condición de contorno es, u(R, t)=0.

• La condición inicial es u(r, 0)=-Ω

Buscamos una solución a la ecuación en derivadas parciales, producto de dos funciones una que dependa de r y otra que dependa de t: u(r, t)=F(r)G(t)

${\displaystyle \begin{array}{l}G(t)\left(\frac{3}{r}\frac{dF}{dr}+\frac{d^{2}F}{d^{2}r}\right)=\frac{\rho }{\eta }F(r)\frac{dG}{dt}\\ \frac{1}{F(r)}\left(\frac{3}{r}\frac{dF}{dr}+\frac{d^{2}F}{d^{2}r}\right)=\frac{\rho }{\eta }\frac{1}{G(t)}\frac{dG}{dt}=-k^2\end{array}}$

Resolvemos la ecuación diferencial de la derecha

${\displaystyle \begin{array}{l}\frac{\rho }{\eta }\frac{1}{G(t)}\frac{dG}{dt}=-k^2\\ G(t)=\exp \left(-\frac{\eta }{\rho }{k}^{2}t\right)\end{array}}$

Resolvemos la ecuación diferencial de la izquierda. Para ello, escribimos la ecuación diferencial en términos de F(r)=y/r

${\displaystyle \begin{array}{l}\frac{dF}{dr}=\frac{\frac{dy}{dr}r-y}{r^2}\\ \frac{d^{2}F}{d{r}^2}=\frac{\left(\frac{d^{2}y}{d{r}^2}r+\frac{dy}{dr}-\frac{dy}{dr}\right)r^2-2r\left(\frac{dy}{dr}r-y\right)}{r^4}=\frac{\frac{d^{2}y}{d{r}^2}{r}^2-2r\frac{dy}{dr}+2y}{r^3}\end{array}}$

La ecuación diferencial en r se convierte en

${\displaystyle r^2\frac{d^{2}y}{d{r}^2}+r\frac{dy}{dr}+(k^2{r}^2-1)y=0}$

Hacemos el cambio de variable x=kr

${\displaystyle x^2\frac{d^{2}y}{d{x}^2}+x\frac{dy}{dx}+(x^2-1)y=0}$

Se trata de la ecuación diferencial de Bessel con n=1, cuya solución es

${\displaystyle y=A{J}_1(x)+B{Y}_1(x)}$

Se descarta el segundo término, ya que Y₁(x)→∞ cuando x→0 ó r→0. La solución es

${\displaystyle \begin{array}{l}y=A{J}_1(x)\\ y=A{J}_1(kr)\end{array}}$

La condición de contorno indica que el recipiente cilíndico se mueve con velocidad angular constante Ω, u(R, t)=0, y(kR)=0

J₁(x)=0

En la página titulada Funciones de Bessel se calculan las raíces de esta ecuación transcendente, λ₁, λ₂, ...λ_n. O bien, k_n=λ_n/R

La solución completa de la ecuación diferencial en derivadas parciales, con la condición de contorno especificada, u(r, t), es la superposición de los productos F_n(r)·G_n(r)

${\displaystyle \begin{array}{l}\omega (r,t)=\Omega +u(r,t)\\ \omega (r,t)=\Omega +{\displaystyle \sum _{n=1}^{\infty }{F}_n(r)G_n(t)}\\ \omega (r,t)=\Omega +\frac{1}{r}{\displaystyle \sum _{n=1}^{\infty }{A}_n{J}_1}\left({\lambda }_n\frac{r}{R}\right)\exp \left(-\frac{\eta }{\rho }\frac{{\lambda }_n^2}{R^2}t\right)\end{array}}$

Los coeficientes A_n se determinan a partir de la condición inicial ω(0,r)=0

${\displaystyle \omega (r\mathrm{,0})=\Omega +\frac{1}{r}{\displaystyle \sum _{n=1}^{\infty }{A}_n{J}_1}\left({\lambda }_n\frac{r}{R}\right)}$

Teniendo en cuenta, las relaciones

• Las relaciones de ortogonalidad de las funciones J₁(x) de Bessel

${\displaystyle \underset{0}{\overset{1}{{\displaystyle \int }}}x{J}_1(k_{m}x)J_1(k_{n}x)dx=0m\ne n}$

Si k(1) y k(2) son dos raíces distintas de la ecuación, J₁(x)=0, se cumple que la integral es nula

x=linspace(0,40,40);
f=@(x) besselj(1,x);
k=raices(f,x); 
 
f=@(x) x.*(besselj(1,k(1)*x).*besselj(1,k(2)*x));
integral(f,0,1)

ans =   2.0786e-17

• La relación

${\displaystyle \underset{0}{\overset{1}{{\displaystyle \int }}}x{J}_1^2(k_{n}x)dx=\frac{1}{2}{J}_0^2(k_n)}$

>> syms x k;
>> int(x*besselj(0,k*x)^2,x,0,1)
ans =besselj(0, k)^2/2 + besselj(1, k)^2/2

Si k es una raíz de J₁(x)=0, el segundo término de la suma es nulo

• La relación

${\displaystyle \underset{0}{\overset{1}{{\displaystyle \int }}}{x}^2{J}_1(k_{n}x)dx=-\frac{J_0(k_n)}{k_n}}$

>> syms x k;
>> int(x^2*besselj(1,k*x),x,0,1)
 ans =(2*besselj(1, k))/k^2 - besselj(0, k)/k

Si k es una raíz de J₁(x)=0, el primer término de la suma es nulo

Teniendo en cuenta, que la variable x=r/R en las tres relaciones anteriores, calculamos los coeficientes A_n

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{R}{\int }}{r}^2\left(\omega (r\mathrm{,0})-\Omega \right)}{J}_1\left({\lambda }_m\frac{r}{R}\right)dr={\displaystyle \underset{0}{\overset{R}{\int }}r\left({\displaystyle \sum _{n=1}^{\infty }{A}_n{J}_1\left({\lambda }_n\frac{r}{R}\right)}\right)J_1\left({\lambda }_m\frac{r}{R}\right)dr}\\ {\displaystyle \underset{0}{\overset{R}{\int }}{r}^2\left(0-\Omega \right)}{J}_1\left({\lambda }_m\frac{r}{R}\right)dr={\displaystyle \sum _{n=1}^{\infty }{A}_n{\displaystyle \underset{0}{\overset{R}{\int }}r{J}_1\left({\lambda }_m\frac{r}{R}\right)}{J}_1\left({\lambda }_n\frac{r}{R}\right)dr}\\ -\Omega {\displaystyle \underset{0}{\overset{R}{\int }}{r}^2}{J}_1\left({\lambda }_n\frac{r}{R}\right)dr=\frac{R^2}{2}{A}_n{J}_0^2\left({\lambda }_n\right)\\ \Omega R^3\frac{J_0\left({\lambda }_n\right)}{{\lambda }_n}=\frac{R^2}{2}{A}_n{J}_0^2\left({\lambda }_n\right)\\ A_n=\frac{2\Omega R}{{\lambda }_n{J}_0\left({\lambda }_n\right)}\end{array}}$

La expresión final de la velocidad angular de rotación ω(r,t) en función del tiempo t de cada una de las capas cilíndricas de fluido es

${\displaystyle \omega (r,t)=\Omega \left\{1+\frac{2R}{r}{\displaystyle \sum _{n=1}^{\infty }\frac{J_1\left({\lambda }_n\frac{r}{R}\right)}{{\lambda }_n{J}_0\left({\lambda }_n\right)}}\exp \left(-{\lambda }_n^2\frac{t}{\tau }\right)\right\},\tau =\frac{R^2\rho }{\eta }}$

λ_n son las raíces de la ecuación transcendente J₁(x)=0. τ se denomina tiempo de relajación, cuando mayor sea este tiempo mas tarde se alcanza aproximadamente el estado estacionario. Para un recipiente de radio R=10 cm

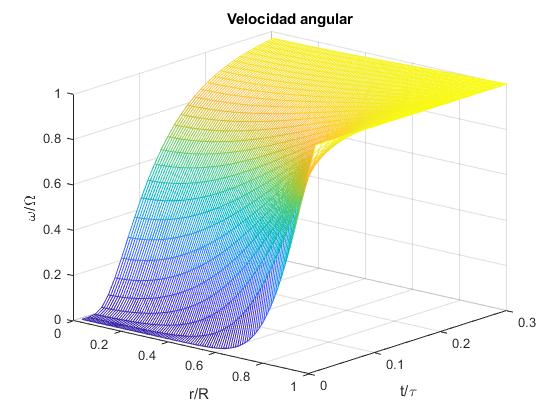
Representamos la velocidad angular adimensional ω(r/R, t/τ)/Ω, en función de la distancia r/R al eje del cilindro y del tiempo t/τ adimensionales

Primero calculamos, las raíces de la ecuación transcendente J₁(x)=0 y definimos una función que devuelve ω/Ω

function w = cilindro_viscosidad(k, r, t)
    w=ones(1,length(r)); 
    for n=1:length(k)
        w=w+2*exp(-k(n)^2*t)*besselj(1,k(n)*r)./(r*k(n)*besselj(0,k(n)));
    end
end

x=linspace(0,100,100);
f=@(x) besselj(1,x);
k=raices(f,x);

tt=0.01:0.01:0.3;
r=0.01:0.01:1;
ww=zeros(length(tt),length(r));
i=1;
for t=tt
    w=cilindro_viscosidad(k, r, t);
    ww(i,:)=w;
    i=i+1;
end
[X,Y]=meshgrid(r,tt);
mesh(X,Y,ww);
xlabel('r/R')
ylabel('t/\tau')
zlabel('\omega/\Omega')
title('Velocidad angular')
view(40,20)

Forma de la superficie del líquido en rotación

En la página titulada Forma de la superficie de un líquido en rotación, demostramos que cuando un recipiente cilíndrico que contiene un líquido se pone en rotación alrededor de su eje con velocidad angular constante Ω, la superficie del líquido adquiere la forma de un paraboloide después de un tiempo suficientemente grande, cuando se alcanza aproximadamente el estado estacionario.

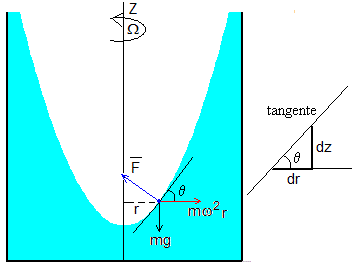
Desde el punto de vista del observador en rotación, las fuerzas que actúan sobre una partícula de fluido de masa m situada en su superficie, a una distancia r del eje de rotación, son

• El peso, $-mg\widehat{k}$
• La fuerza centrífuga, $m{\omega }^{2}r\widehat{i}$
• La fuerza $\overrightarrow{R}$ que ejercen las otras partículas de fluido sobre la partícula considerada

Desde el punto de vista del observador no inercial, la partícula está en equilibrio, de modo que la resultante de las fuerzas que actúan sobre la partícula debe ser cero

${\displaystyle \overrightarrow{R}-mg\widehat{k}+m{\omega }^{2}r\widehat{i}=0}$

La forma de la superficie del líquido en equilibrio será tal que $\overrightarrow{R}$ es perpendicular a la tangente a la curva en cada punto a una distancia r del eje de rotación. Como vemos en la figura

${\displaystyle \tan \theta =\frac{dz}{dr}=\frac{m{\omega }^{2}r}{mg}}$

Integrando tenemos

${\displaystyle z(r,t)=\frac{1}{g}{\displaystyle \int r{\omega }^2(r,t)dr+c}}$

En el estado estacionario, la velocidad angular de todas las capas cilíndicas de fluido es la misma Ω

${\displaystyle \begin{array}{l}z(r,\infty )=\frac{{\Omega }^2}{g}{\displaystyle \int rdr+c}\\ z(r)=\frac{{\Omega }^2}{2g}{r}^2+c\end{array}}$

Establemos un Sistema de Referencia en el eje del recipiente, eje Z, el otro eje coincide con la superficie libre cuando el líquido está en reposo, el volumen de fluido en el estado inicial es cero. Supondremos que el fluido es incompresible y su volumen se mantiene constante

${\displaystyle {\displaystyle \underset{0}{\overset{R}{\int }}2\pi rz(r,t)}dr=0}$

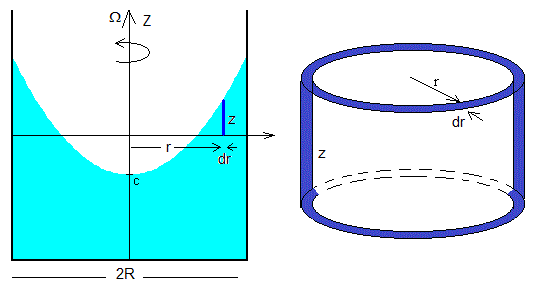
Donde z(r,t) es la altura de fluido sobre la superficie plana y horizontal (que puede ser positiva o negativa) a la distancia r del eje de rotación y en el instante t

En el estado estacionario, integramos para obtener la constante c y la ecuación del paraboloide de revolución

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{R}{\int }}2\pi r\left(\frac{{\Omega }^2}{2g}{r}^2+c\right)}dr=0\\ c=-\frac{{\Omega }^2}{4g}{R}^2\\ z(r)=\frac{{\Omega }^2}{2g}\left(r^2-\frac{R^2}{2}\right)\end{array}}$

En el estado transitorio, la velocidad angular no es constante, por tanto, la forma de la superficie pasará de plana y horizontal en el estado inicial t=0 (el recipiente en reposo) a la forma de paraboloide de revolución cuando se alcance el estado estacionario, t→∞ (el recipiente y el fluido que contiene se mueven con velocidad angular constante Ω)

Las dos integrales anteriores se calculan numéricamente mediante la función trapz de MATLAB, o emplendo el procedimiento de Simpson en el programa interactivo más abajo

En el estado estacionario, el vértice de la parábola se encuentra en z₀=Ω²R²/(4g) por debajo del origen. Dividimos todas las alturas z(r,t) por esta cantidad para que la altura del vértice del paraboloide en el estado estacionario se encuentre en -1. La ecuación del paraboloide de revolución es

${\displaystyle \frac{z(r)}{z_0}=2\frac{r^2}{R^2}-1}$

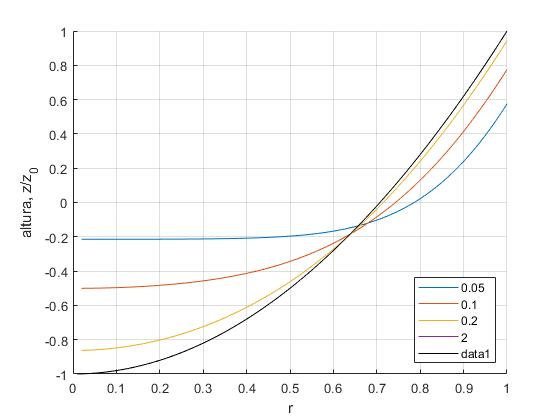
Dibujamos el perfil el perfil z(r,t)/z₀ de la superficie (la mitad, ya que es simétrica respecto del eje Z) del fluido en los instantes adimensionales t/τ=0.05, 0.1, 0.2 y 2

Apreciamos que en el instante t/τ=2, está muy próximo al estado estacionario, la curva de color morado se confunde con la de color negro (parábola)

x=linspace(0,100,100);
f=@(x) besselj(1,x);
k=raices(f,x);

hold on
r=0.01:0.01:1;
integ=zeros(1,length(r));
z=zeros(1,length(r));
for t=[0.05,0.1, 0.2,2]
    w=cilindro_viscosidad(k, r, t);
    for i=1:length(r)
        integ(i)=w(i).^2.*r(i);
    end
     for i=2:length(r) %calcula las alturas z
        z(i)=trapz(r(1:i),integ(1:i))*4;
     end
     c=-2*trapz(r,r.*z); %constante c
    plot(r(2:end),z(2:end)+c,'displayName',num2str(t))
end
plot(r,(2*r.^2-1),'k') %cuando t->inf
hold off
grid on
xlabel('r')
ylabel('altura, z/z_0')
legend('-DynamicLegend','location','southeast')

Se detiene el recipiente cilíndrico

El cilindro y el fluido que contiene giran con velocidad angular constante Ω. En el instante t=0, se detiene el recipiente abruptamente, ω(r,0)=Ω. Las distintas capas de fluido continuarán moviéndose hasta que en un tiempo muy largo, teóricamente infinito, se detienen, ω(r,∞)=0.

Se resuelve la ecuación diferencial en derivadas parciales de modo semejante, ya que se han intercambiado las condición inicial y la de contorno.

${\displaystyle \frac{3}{r}\frac{\partial \omega }{\partial r}+\frac{{\partial }^2\omega }{{\partial }^{2}r}=\frac{\rho }{\eta }\frac{\partial \omega }{\partial t}}$

Definimos la función u(r,t)=ω(r,t)-ω(r,∞)=ω(r,t)-0=ω(r,t). En términos de esta nueva función, la ecuación diferencial se escribe

${\displaystyle \frac{3}{r}\frac{\partial u}{\partial r}+\frac{{\partial }^{2}u}{{\partial }^{2}r}=\frac{\rho }{\eta }\frac{\partial u}{\partial t}}$

• La condición de contorno es, u(R, t)=0.

• la condición inicial es u(r, 0)=Ω

Buscamos una solución a la ecuación en derivadas parciales, producto de dos funciones una que dependa de r y otra que dependa de t: u(r, t)=F(r)G(t)

${\displaystyle G(t)=\exp \left(-\frac{\eta }{\rho }{k}^{2}t\right)}$

La condición de contorno indica que el recipiente cilíndico está en reposo, u(R, t)=0, y(kR)=0

J₁(x)=0

La solución completa de la ecuación diferencial en derivadas parciales, con la condición de contorno especificada, u(r, t), es la superposición de los productos F_n(r)·G_n(r)

${\displaystyle \begin{array}{l}\omega (r,t)=u(r,t)\\ \omega (r,t)={\displaystyle \sum _{n=1}^{\infty }{F}_n(r)G_n(t)}\\ \omega (r,t)=\frac{1}{r}{\displaystyle \sum _{n=1}^{\infty }{A}_n{J}_1}\left({\lambda }_n\frac{r}{R}\right)\exp \left(-\frac{\eta }{\rho }\frac{{\lambda }_n^2}{R^2}t\right)\\ \omega (r\mathrm{,0})=\frac{1}{r}{\displaystyle \sum _{n=1}^{\infty }{A}_n{J}_1}\left({\lambda }_n\frac{r}{R}\right)\end{array}}$

Los coeficientes A_n se determinan a partir de la condición inicial ω(0,r)=Ω

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{R}{\int }}{r}^2\omega (r\mathrm{,0})}{J}_1\left({\lambda }_m\frac{r}{R}\right)dr={\displaystyle \underset{0}{\overset{R}{\int }}r\left({\displaystyle \sum _{n=1}^{\infty }{A}_n{J}_1\left({\lambda }_n\frac{r}{R}\right)}\right)J_1\left({\lambda }_m\frac{r}{R}\right)dr}\\ {\displaystyle \underset{0}{\overset{R}{\int }}{r}^2\omega (r\mathrm{,0})}{J}_1\left({\lambda }_m\frac{r}{R}\right)dr={\displaystyle \sum _{n=1}^{\infty }{A}_n{\displaystyle \underset{0}{\overset{R}{\int }}r{J}_1\left({\lambda }_m\frac{r}{R}\right)}{J}_1\left({\lambda }_n\frac{r}{R}\right)dr}\\ \Omega {\displaystyle \underset{0}{\overset{R}{\int }}{r}^2}{J}_1\left({\lambda }_n\frac{r}{R}\right)dr=\frac{R^2}{2}{A}_n{J}_0^2\left({\lambda }_n\right)\\ -\Omega R^3\frac{J_0\left({\lambda }_n\right)}{{\lambda }_n}=\frac{R^2}{2}{A}_n{J}_0^2\left({\lambda }_n\right)\\ A_n=-\frac{2\Omega R}{{\lambda }_n{J}_0\left({\lambda }_n\right)}\end{array}}$

La expresión final de la velocidad angular de rotación ω(r,t) en función del tiempo t de cada una de las capas cilíndicas de fluido es

${\displaystyle \omega (r,t)=-\frac{2\Omega R}{r}{\displaystyle \sum _{n=1}^{\infty }\frac{J_1\left({\lambda }_n\frac{r}{R}\right)}{{\lambda }_n{J}_0\left({\lambda }_n\right)}}\exp \left(-{\lambda }_n^2\frac{t}{\tau }\right),\tau =\frac{R^2\rho }{\eta }}$

λ_n son las raíces de J₁(x)=0 y τ es el tiempo de relajación, cuando mayor sea este tiempo más tarde se alcanza aproximadamente el estado estacionario.

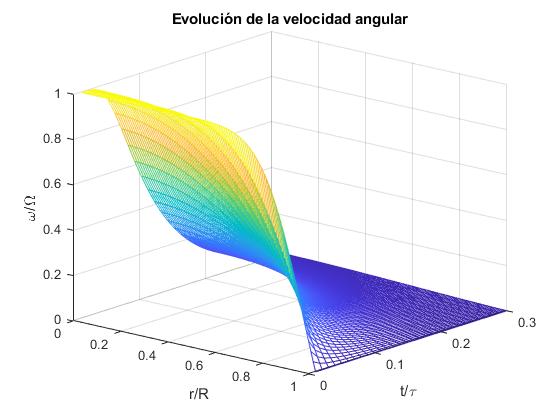
Representamos la velocidad angular adimensional ω(r/R, t/τ)/Ω, en función de la distancia r/R y del tiempo t/τ adimensionales

Primero calculamos, las raíces de la ecuación transcendente J₁(x)=0 y definimos una función que devuelve ω/Ω

function w = cilindro_viscosidad_1(k, r, t)
    w=zeros(1,length(r)); 
    for n=1:length(k)
        w=w-2*exp(-k(n)^2*t)*besselj(1,k(n)*r)./(r*k(n)*besselj(0,k(n)));
    end
end

x=linspace(0,100,100);
f=@(x) besselj(1,x);
k=raices(f,x);

tt=0.01:0.01:0.3;
r=0.01:0.01:1;
ww=zeros(length(tt),length(r));
i=1;
for t=tt
    w=cilindro_viscosidad_1(k, r, t);
    ww(i,:)=w;
    i=i+1;
end
[X,Y]=meshgrid(r,tt);
mesh(X,Y,ww);
xlabel('r/R')
ylabel('t/\tau')
zlabel('\omega/\Omega')
title('Evolución de la velocidad angular')
view(40,20)

Forma de la superficie del líquido en rotación

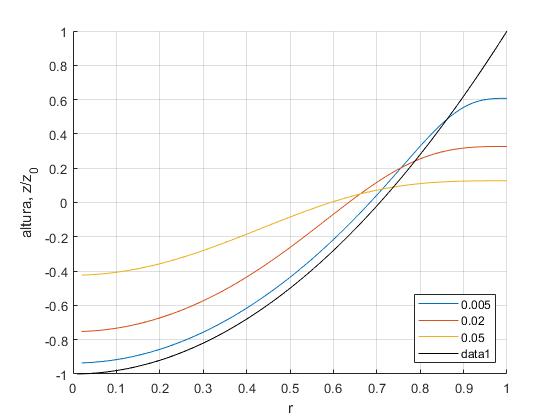
Dibujamos el perfil z(r,t)/z₀ de la superficie (la mitad, ya que es simétrica respecto del eje Z) del fluido en los instantes adimensionales t/τ=0.0005, 0.02, 0.05

En el instante inicial, t=0, se dibuja el perfil parabólico en color negro, cuando el recipiente y el fluido giran con la misma velocidad angular Ω. A medida que transcurre el tiempo, el perfil va tendiendo hacia la superficie plana horizontal, que se alcanza el en estado estacionario, cuando el fluido se ha detenido

x=linspace(0,100,100);
f=@(x) besselj(1,x);
k=raices(f,x);

hold on
r=0.01:0.01:1;
integ=zeros(1,length(r));
z=zeros(1,length(r));
for t=[0.005, 0.02,0.05]
    w=cilindro_viscosidad_1(k, r, t);
    for i=1:length(r)
        integ(i)=w(i).^2.*r(i);
    end
     for i=2:length(r)
        z(i)=trapz(r(1:i),integ(1:i))*4;
     end
     c=-2*trapz(r,r.*z); %constante c
    plot(r(2:end),z(2:end)+c,'displayName',num2str(t))
end
plot(r,(2*r.^2-1),'k') %cuando t->inf
hold off
grid on
xlabel('r')
ylabel('altura, z/z_0')
legend('-DynamicLegend','location','southeast')

Actividades

Se elige una de las dos situaciones descritas en esta página

• Con el fluido en reposo dentro del recipiente, se pone en marcha el recipiente y se mantien girando con velocidad angular constante Ω, activando el botón de radio titulado Se da una velocidad al recipiente
• El recipiente y el fluido que lo contiene, giran con velocidad angular constante Ω. Se detiene el recipiente, activando el botón de radio titulado Se detiene

Se introduce

• El tiempo de relajación τ en el segundos, en el control titulado Tiempo relajación
• El radio del recipiente se ha fijado en R=1

A la izquierda, se muestra el movimiento de las partículas de fluido situados a distancias variables del eje del cilindro. A la derecha, el perfil z(r,t)/z₀ de la superficie (la mitad, ya que es simétrica respecto del eje Z) del fluido

En la parte derecha, la curva de color rojo representa:

• el estado estacionario final z(r,∞)/z₀, para la primera situación
• el estado inicial z(r,0)/z₀, para la segunda

Referencias

Vladimir Ivchenko. On the unsteady rotating fluid flow in a uniformly rotating or fixed vertical cylinder. Eur. J. Phys. 41(2020) 035006