La ley de Poiseuille para los gases

Supongamos un tubo capilar de radio r y longitud L por el cual fluye un gas cuando la diferencia de presión en sus extremos es p-p₀

La ley de Poiseuille que hemos deducido para un fluido viscoso incomprensible, afirma que el gasto G=dV/dt (volumen de fluido que atraviesa la sección normal del capilar en la unidad de tiempo) es directamente proporcional al gradiente de presión a lo largo del tubo, es decir al cociente (p-p₀)/L.

${\displaystyle \frac{dV}{dt}=\frac{\pi r^4}{8\eta }\frac{p-p_0}{L}}$

Ahora bien, para un gas que fluye a través del tubo capilar, el volumen de gas que entra en la unidad de tiempo a una presión p no es igual al volumen que sale del tubo a la presión p₀ (atmosférica) debido a la comprensibilidad de los gases. Sin embargo, la masa de gas que entra en la unidad de tiempo es igual a la masa de gas que sale en la unidad de tiempo.

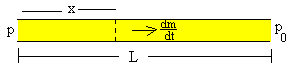
Escribimos la ley de Poiseuille de la forma

${\displaystyle \frac{dV}{dt}=\frac{\pi r^4}{8\eta }\frac{dp}{dx}}$

dV/dt es el volumen de gas que atraviesa la sección normal del tubo capilar situada a una distancia x del extremo del tubo, en la unidad de tiempo. dp/dx es el gradiente de presión en dicha posición.

Teniendo en cuenta la ley de los gases ideales p·V=nRT

• n es el número de moles n=m/M ,

• m es la masa de gas contenida en el volumen V,

• M el peso molecular,

• R=8.3143 J/(K·mol) la constante de los gases

• T la temperatura absoluta.

${\displaystyle p·dV=\frac{dm}{M}RT}$

La ley de Poiseuille se escribe

${\displaystyle \left(\frac{dm}{dt}\right)dx=-\frac{M}{RT}\frac{\pi r^4}{8\eta }p·dp}$

El signo menos aparece por que la presión p del gas disminuye a medida que sale por el tubo capilar

Integramos esta ecuación teniendo en cuenta que dm/dt es constante a lo largo del tubo capilar. La presión en el extremo x=0 del tubo capilar es p y la presión en el otro extremo x=L es p₀ (atmosférica).

${\displaystyle \begin{array}{l}\left(\frac{dm}{dt}\right){\displaystyle \underset{0}{\overset{L}{\int }}dx}=-\frac{M}{RT}\frac{\pi r^4}{8\eta }{\displaystyle \underset{p}{\overset{p_0}{\int }}p·dp}\\ \left(\frac{dm}{dt}\right)=\frac{M}{RT}\frac{\pi r^4}{16\eta L}\left(p^2-p_0^2\right)\end{array}}$

El dispositivo experimental

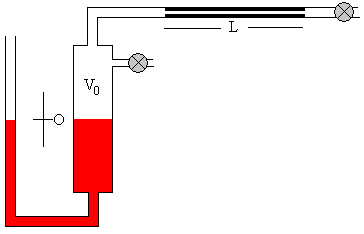
En la figura, se muestra la situación inicial del dispositivo. El manómetro de mercurio a la izquierda, el volumen V₀ de la región comprendida entre el mercurio y el tubo capilar, el tubo capilar de longitud L y radio r.

El gas cuya viscosidad se va a medir, se introduce en la región comprendida entre el mercurio del manómetro y el capilar, hasta alcanzar la presión p deseada.

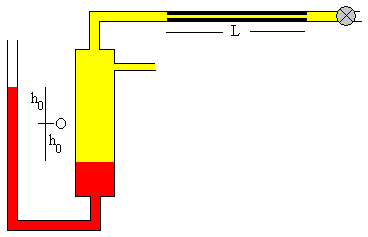
• La presión inicial del gas es

p=p₀+2ρgh₀

• El volumen inicial del gas es

V=V₀+S·h₀

Siendo S la sección del manómetro

Cuando se alcanza la presión deseada, se abre la llave situada en el extremo del capilar, el gas fluye a través del mismo impulsado por la diferencia de presión p-p₀, la diferencia de alturas 2h de los niveles de mercurio en las dos ramas del manómetro va disminuyendo.

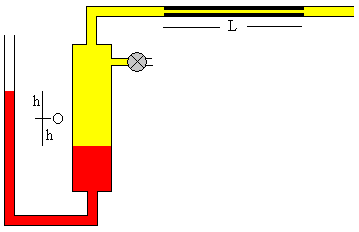
En el instante t la diferencia de alturas de los niveles de mercurio en las dos ramas del manómetro es 2h.

La presión p y el volumen V del gas contenido en el recipiente, va cambiando con el tiempo. La masa m de gas contenido en el recipiente, disminuye. La masa que atraviesa la sección normal del capilar en la unidad de tiempo es, aplicando la ley de los gases ideales

${\displaystyle \left(\frac{dm}{dt}\right)=-\frac{M}{RT}\frac{d(pV)}{dt}}$

Aplicando la ley de Poiseuille al movimiento de un gas a través de un capilar

${\displaystyle \begin{array}{l}-\frac{M}{RT}\frac{d(pV)}{dt}=\frac{M}{RT}\frac{\pi r^4}{16\eta L}\left(p^2-p_0^2\right)\\ {\displaystyle \underset{0}{\overset{t}{\int }}dt}=-\frac{16\eta L}{\pi r^4}{\displaystyle \underset{h_0}{\overset{h}{\int }}\frac{V·dp+p·dV}{p^2-p_0^2}}=\frac{16\eta L}{\pi r^4}{\displaystyle \underset{h}{\overset{h_0}{\int }}\frac{V·dp+p·dV}{p^2-p_0^2}}\end{array}}$

Para integrar expresamos el volumen V del gas y su presión p en función de la variable h.

p=p₀+2ρgh     dp=2ρg·dh
V=V₀+S·h       dV=S·dh

p₀= ρgH, es la presión atmosférica. H=76 cm altura de la columna de mercurio

${\displaystyle \begin{array}{l}t=\frac{16\eta L}{\pi r^4}{\displaystyle \underset{h}{\overset{h_0}{\int }}\frac{(2V_0+4Sh+SH)}{4\rho gh(H+h)}}dh=\frac{4\eta L}{\rho g\pi r^4}{\displaystyle \underset{h}{\overset{h_0}{\int }}\frac{(2V_0+4Sh+SH)}{h(H+h)}}dh=\\ \frac{4\eta L}{\rho g\pi r^4}\left\{\left(S+\frac{2V_0}{H}\right){\displaystyle \underset{h}{\overset{h_0}{\int }}\frac{dh}{h}+\left(3S-\frac{2V_0}{H}\right)}{\displaystyle \underset{h}{\overset{h_0}{\int }}\frac{dh}{H+h}}\right\}=\\ \frac{4\eta L}{\rho g\pi r^4}\left\{\left(S+\frac{2V_0}{H}\right)\ln \left(\frac{h_0}{h}\right)+\left(3S-\frac{2V_0}{H}\right)\ln \left(\frac{H+h_0}{H+h}\right)\right\}\end{array}}$

La diferencia ente los niveles de mercurio en las dos ramas del manómetro es 2h₀ en el instante t=0. Al cabo de un cierto tiempo t, ha salido una cierta cantidad de gas por el tubo-capilar y la presión ha disminuido, la diferencia entre los niveles de mercurio en las dos ramas del manómetro es 2h.

Manteniendo fijos h₀ y h en las medidas que se realizan con los gases disponibles, vemos que el tiempo t es proporcional a la viscosidad η,  la constante de proporcionalidad K se denomina constante del aparato. Se determina, habitualmente, a partir del dato de la viscosidad conocida de un gas (por ejemplo, el aire).

${\displaystyle t=K\eta K=\frac{4L}{\rho g\pi r^4}\left\{\left(S+\frac{2V_0}{H}\right)\ln \left(\frac{h_0}{h}\right)+\left(3S-\frac{2V_0}{H}\right)\ln \left(\frac{H+h_0}{H+h}\right)\right\}}$

La diferencia de alturas 2h ente los niveles de mercurio en las dos ramas del manómetro, es una función implícita del tiempo t.

L=0.85; %longitud capilar
S=3.89e-4; % area de la sección del manómetro
r=0.127e-3; %radio capilar
V0=81.65e-6; %volumen inicial
rho=13550; %densidad del mercurio
H=0.76; %presión atmosférica igual a 76 cm de altura de mercurio
h0=0.20; %altura inicial que marca el manómetro
eta=8.85e-6; %viscosidad del hidrógeno

h=0.01:0.01:0.2;
f=@(h) eta*(4*L/(rho*9.8*pi*r^4))*((S+2*V0/H)*log(h0./h)
+(3*S-2*V0/H)*log((H+h0)./(H+h)));
t=f(h);
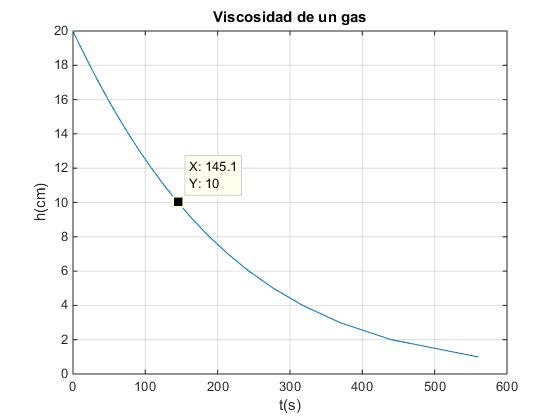
plot(t,100*h)
grid on
xlabel('t(s)')
ylabel('h(cm)')
title('Viscosidad de un gas')

Actividades

• Se selecciona el gas, en el control titulado Gases

Los datos que se ha fijado en el programa interactivo (tomadas parcialmente del segundo artículo citado en las referencias) son los siguientes:

• Densidad del mercurio, ρ=13.55 g/cm³

• Longitud del capilar, L=85.0 cm

• Radio del capilar, r=0.127 mm

• Área de la sección del manómetro, S=3.89 cm²

• Volumen inicial cuando se introduce el gas, V₀=81.65 cm³

• La presión atmosférica equivale a la presión de una columna de mercurio de H=76 cm de altura.

Se pulsa el botón titulado Nuevo y a continuación, Abre

Se cierra la llave situada en el extremo del tubo capilar. Se abre la llave de admisión del gas y la región comprendida entre el mercurio y el tubo capilar se va llenando de gas. La presión y el volumen del gas aumentan. Cuando el manómetro marca una altura h₀=20 cm,

• La presión inicial del gas es p=p₀+2ρgh₀
• El volumen inicial del gas es V=V₀+S·h₀

Se pulsa el botón titulado ►

Se cierra la llave de admisión del gas y se abre la llave en el extremo del tubo capilar, de modo que el gas empieza a salir. La presión y el volumen del gas disminuyen, cuando el nivel del mercurio en el manómetro señala una altura h se pulsa el botón titulado Ⅱ

Se anota h y el tiempo t. Se calcula la viscosidad η del gas.

Ejemplo

• Se elige Hidrógeno

• Se introduce el gas a la máxima presión. El manómetro marca h₀=20 cm

• Se deja salir el gas a través del tubo capilar

• Cuando el manómetro marca h=10 cm, ha transcurrido un tiempo t=145.0 s

${\displaystyle \begin{array}{l}t=\eta \frac{4L}{\rho g\pi r^4}\left\{\left(S+\frac{2V_0}{H}\right)\ln \left(\frac{h_0}{h}\right)+\left(3S-\frac{2V_0}{H}\right)\ln \left(\frac{H+h_0}{H+h}\right)\right\}\\ 145.0=\eta \frac{4·0.85}{13550·9.8·\pi {(0.127·{10}^{-3})}^4}\left\{\begin{array}{l}\left(3.89·{10}^{-4}+\frac{2·81.65·{10}^{-6}}{0.76}\right)\ln \left(\frac{0.2}{0.1}\right)+\\ \left(3·3.89·{10}^{-4}-\frac{2·81.65·{10}^{-6}}{0.76}\right)\ln \left(\frac{0.76+0.2}{0.76+0.1}\right)\end{array}\right\}\end{array}}$

η=8.84·10^-6 kg/(m·s)

Referencias

Nienart L., Measuring the viscosity of gases. Am. J. Phys. 62 (6) June 1994, pp. 566-568

Cronin D. J., Temperature and pressure dependence of viscosity of gases. Am. J. Phys. 33 (1965) pp. 835-840