Régimen laminar y régimen turbulento

Hemos estudiado el comportamiento de un fluido perfecto (ecuación de Bernoulli) y el comportamiento de un fluido viscoso en régimen laminar (ecuación de Poiseuille). Sin embargo, no existe una teoría análoga que describa el comportamiento de los fluidos en régimen turbulento, o que explique la transición de régimen laminar a turbulento.

El objetivo de estas página es la de familiarizar al lector con el denominado número de Reynolds, y la importancia que tiene a la hora de definir si un determinado fluido está en régimen laminar, turbulento, o en la transición entre ambos regímenes.

Los resultados experimentales se ajustan notablemente a las predicciones del flujo laminar para valores bajos del número de Reynolds R, y se ajustan a las predicciones del flujo turbulento para valores de R mayores que 4400 aproximadamente. Mientras que los valores intermedios de R cubren una amplia región en la que se produce la transición de flujo y ninguna de las dos teorías reproduce satisfactoriamente los resultados experimentales.

El número de Reynolds es el número adimensional

$R = \frac{ρ D v}{η}$

Donde D es el diámetro del tubo, ρ la densidad del fluido, y η la viscosidad, y v su velocidad.

Para fluidos no ideales la ecuación de Bernoulli toma la forma

$(p_{1} + ρ g y_{1} + \frac{1}{2} ρ v_{1}^{2}) - (p_{2} + ρ g y_{2} + \frac{1}{2} ρ v_{2}^{2}) = ρ H$

donde el término H se denomina "pérdida de carga". Si el fluido es ideal H=0,

Dispositivo experimental

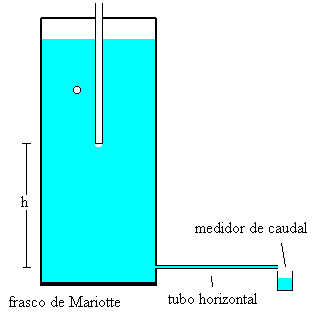
El dispositivo experimental consta de un frasco de Mariotte de 27.4 cm de diámetro y 57.5 cm de altura, que desagua a través de un tubo horizontal de longitud L y diámetro D, que se inserta en un orificio situado en la parte inferior del frasco.

Se dispone de un conjunto de tres tubos intercambiables de los siguientes diámetros y longitudes

Tubo	Longitud (cm)	Diámetro (mm)
1	29.3	2.42
2	56.7	3.96
3	50.5	5.36

La velocidad v de salida del agua por el tubo horizontal se puede determinar mediante simples medidas de caudal.

En la experiencia real, se recogerán los datos correspondientes a la velocidad v de salida del agua por el tubo horizontal en función de la altura h del tubo del frasco de Mariotte. Se compararán los valores "experimentales" con las predicciones del flujo laminar y del flujo turbulento.

La utilización de tubos de vidrio de dimensiones diferentes permite comprobar que la transición del régimen laminar al turbulento es independiente de éstas, dependiendo únicamente, del valor crítico de un parámetro adimensional: el número de Reynolds.

El frasco de Mariotte

Uno de los ejemplos más ilustrativos de la ecuación de Bernoulli es el frasco de Mariotte. Este sencillo dispositivo nos proporciona un caudal constante mientras el nivel de líquido en el recipiente esté por encima del extremo inferior del tubo vertical.

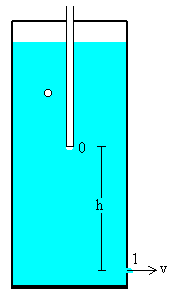
Aplicando la ecuación de Bernoulli a los puntos 0 (extremos inferior del tubo vertical) y 1 (orificio de salida o entrada del tubo horizontal), tendremos

$p_{0} + ρ g y_{0} + \frac{1}{2} ρ v_{0}^{2} = p_{1} + ρ g y_{1} + \frac{1}{2} ρ v_{1}^{2}$

Teniendo en cuenta que la diferencia de alturas y₀-y₁=h, que la presión p₀ en el extremo inferior del tubo vertical es la presión atmosférica p_at, y que v₀≈0, ya que la sección del recipiente es mucho mayor que la sección del orificio de salida.

$p_{a t} + ρ g h = p_{1} + \frac{1}{2} ρ v_{1}^{2}$ (1)

El tubo horizontal

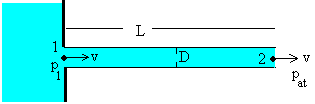
Para un tubo horizontal de sección uniforme la ecuación de continuidad implica que v₁=v₂=v. Los puntos 1 y 2 están a la misma altura y₁=y₂, y la presión a la salida del tubo es la atmosférica p₂=p_at.

p₁-p_at=ρ (H_L+H_l) (2)

Siendo H= H_L+H_l las pérdidas totales de carga.

Combinando las ecuaciones (1) y (2) llegamos a la ecuación que relaciona v y h.

$(H_{L} + H_{l}) = g h - \frac{1}{2} v^{2}$

Hay dos expresiones para la pérdida H_L una que describe el comportamiento del fluido en régimen laminar y otra que describe el comportamiento del fluido en régimen turbulento como veremos más adelante.

Otras pérdidas

Bajo el término H_l se agrupan otras pérdidas menores debidas a la entrada y salida del fluido por el tubo horizontal, y que son independientes de que el régimen del fluido sea laminar o turbulento.

$H_{l} = k \frac{v^{2}}{2}$

siendo comunes los valores de k=0.78 en la entrada y k=1 en la salida. En total tenemos que

$H_{l} = 1.78 \frac{v^{2}}{2}$

Fluido en régimen laminar

A la diferencia de presión p₁-p₂ en los extremos del tubo horizontal dividida entre la densidad ρ del fluido, se le denomina pérdida de carga H_L en el flujo laminar

$H_{L} = \frac{p_{1} - p_{2}}{ρ} = \frac{8 η L}{ρ π r^{4}} G = \frac{8 η L}{ρ r^{2}} v = \frac{32 η L}{ρ D^{2}} v$

Siendo L y D la longitud y el diámetro del tubo horizontal y η la viscosidad del fluido.

Teniendo en cuenta las expresiones de las pérdidas de carga H_L en el flujo laminar y las pérdidas H_ldebidas a la entrada y salida del fluido por el tubo horizontal, se expresa

$2.78 D^{2} ρ v^{2} + 64 L η v - 2 g h D^{2} ρ = 0$

Ejemplo:

Para el agua a 20ºC los datos son ρ=1000 kg/m³ y η=1.002·10^-3 kg/(ms)

Volvemos al ejemplo del apartado anterior. Supongamos que utilizamos el primer tubo, L=29.3 cm y D=2r=2.42 mm, y que la altura h=30 cm

Resolvemos la ecuación de segundo grado para calcular v, tomando la raíz positiva v=0.988 m/s. El caudal es G=πr²v=4.5 litros/s

El número de Reynolds vale

$R = \frac{ρ D v}{η} R = \frac{1000 \cdot 2.42 \cdot 10^{- 3} \cdot 0.988}{1.002 \cdot 10^{- 3}} = 2385$

Fluido en régimen turbulento

En este caso, se emplea la fórmula empírica de Blasius válida para tubos lisos y para valores del número de Reynolds hasta 10⁵.

$H_{L} = \frac{0.158}{R^{1 / 4}} \frac{L}{D} v^{2}$

Expresaremos H_L en términos de las variables básicas en vez del número de Reynolds R. Las pérdidas H_ldebidas a la entrada y salida del fluido por el tubo horizontal tienen la misma expresión en el régimen laminar y en el turbulento

$2.78 ρ^{1 / 4} D^{5 / 4} v^{9 / 4} + 0.316 η^{1 / 4} L v^{2} - 2 g h ρ^{1 / 4} D^{5 / 4} v^{1 / 4} = 0$

Se resuelve mediante procedimientos numéricos

Simulación de la experiencia

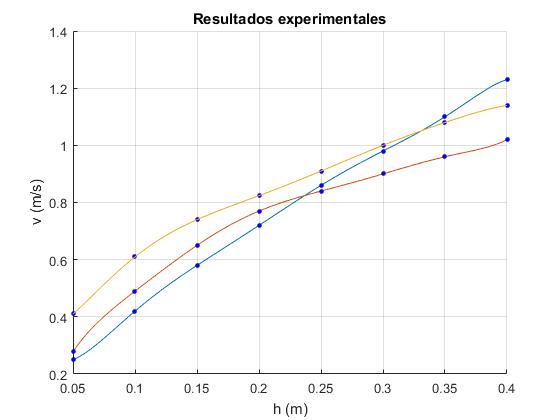
Para simular la experiencia real, el programa interactivo ha utilizado los valores experimentales suministrados por uno de los autores, J. A. Maroto, del artículo citado en las referencias

Para cada uno de los tubos se suminsitraron los datos de la velocidad v de salida del agua en función de la altura h del tubo de Mariotte. Para calcular otros valores de la velocidad v para una altura h que no está en la tabla se ha utilizado la fórmula de interpolación de Lagrange

hM=[0.05, 0.1, 0.15, 0.2, 0.25, 0.30, 0.35, 0.4];
vM=[[0.25, 0.42, 0.58, 0.72, 0.86, 0.98, 1.10, 1.23]; %tubo 1
    [0.278, 0.49, 0.65, 0.77, 0.84, 0.90, 0.96, 1.02]; %tubo 2
    [0.41, 0.61, 0.74, 0.824, 0.91, 1.00, 1.08, 1.14]]; %tubo 3
%interpolación de Lagrange                      
A=vander(hM);
hold on
for i=1:3 
    p=A\vM(i,:)';
    f=@(xx) polyval(p,xx);
    plot(hM,vM,'bo','markersize',3,'markerfacecolor','b')
    fplot(f,[hM(1),hM(end)])
end
hold off
xlabel('h (m)')
ylabel('v (m/s)')
grid on
title('Resultados experimentales')

Flujo laminar y turbulento

La velocidad v de salida del agua por el tubo es una función de la altura h del tubo de Mariotte.

Para el flujo laminar la ecuación es

$2.78 D^{2} ρ v^{2} + 64 L η v - 2 g h D^{2} ρ = 0$

Para el flujo turbulento la ecuación es

$2.78 ρ^{1 / 4} D^{5 / 4} v^{9 / 4} + 0.316 η^{1 / 4} L v^{2} - 2 g h ρ^{1 / 4} D^{5 / 4} v^{1 / 4} = 0$

Para el agua a 20ºC los datos son densidad ρ=1000 kg/m³ y viscosidad η=1.002·10^-3 kg/(ms)

Vamos a comprobar si el flujo de agua por los tubo 1, 2 ó 3 es laminar o turbulento, o ni uno ni el otro.

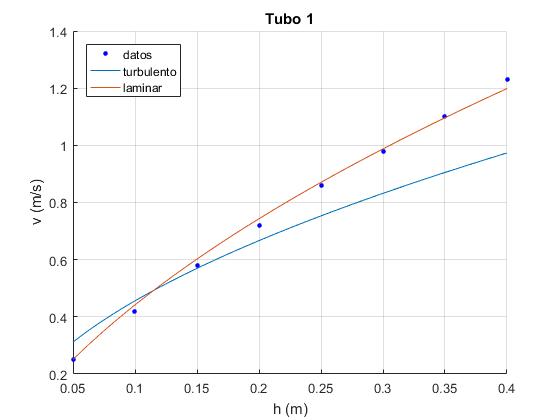
%datos experimentales
hM=0.05:0.05:0.4; %altura
vM=[0.25, 0.42, 0.58, 0.72, 0.86, 0.98, 1.10, 1.23]; %velocidad 
hold on
plot(hM,vM,'bo','markersize',3,'markerfacecolor','b')

L=29.3; %longitud del tubo 1 en cm
D=2.42;  %diámetro del tubo 1 en mm

h=0.05:0.01:0.4; %alturas
v=zeros(1,length(h));
hold on
%régimen turbulento
i=1;
for x=h
    f=@(v) (2.78*D^1.25/1000)*v^2.25+5.6222e-4*L*v^2-
(2*9.8*x*D^1.25/1000)*v^0.25;
    v(i)=fzero(f,[0.1,2]); %velocidades
    i=i+1;
end
plot(h,v)
%régimen laminar
i=1;
for x=h
    a=2.78*D^2/1000;
    b=64*L*1.002e-5;
    c=-2*9.8*x*D^2/1.0e3;
    v(i)=(-b+sqrt(b^2-4*a*c))/(2*a); %velocidades
    i=i+1;
end
plot(h,v)
hold off
legend('datos', 'turbulento', 'laminar', 'location','northwest')
xlabel('h (m)')
ylabel('v (m/s)')
grid on
title('Tubo 1')

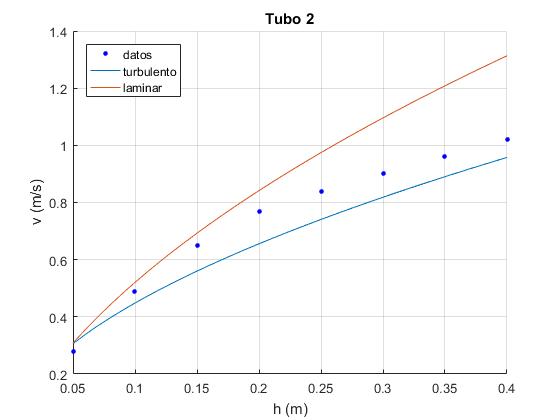
%datos experimentales
hM=0.05:0.05:0.4; %altura
vM=[0.278, 0.49, 0.65, 0.77, 0.84, 0.90, 0.96, 1.02]; %velocidad 
hold on
plot(hM,vM,'bo','markersize',3,'markerfacecolor','b')

L=56.7; %longitud del tubo 2 en cm
D=3.96;  %diámetro del tubo 2 en mm

h=0.05:0.01:0.4; %alturas
v=zeros(1,length(h));
hold on
  %régimen turbulento
i=1;
for x=h
    f=@(v) (2.78*D^1.25/1000)*v^2.25+5.6222e-4*L*v^2-
(2*9.8*x*D^1.25/1000)*v^0.25;
    v(i)=fzero(f,[0.1,2]); %velocidades
    i=i+1;
end
plot(h,v)
%régimen laminar
i=1;
for x=h
    a=2.78*D^2/1000;
    b=64*L*1.002e-5;
    c=-2*9.8*x*D^2/1.0e3;
    v(i)=(-b+sqrt(b^2-4*a*c))/(2*a); %velocidades
    i=i+1;
end
plot(h,v)
hold off
legend('datos', 'turbulento', 'laminar', 'location','northwest')
xlabel('h (m)')
ylabel('v (m/s)')
grid on
title('Tubo 2')

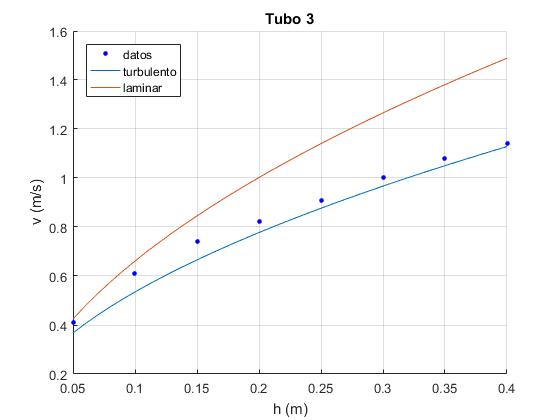
%datos experimentales
hM=0.05:0.05:0.4; %altura
vM=[0.41, 0.61, 0.74, 0.824, 0.91, 1.00, 1.08, 1.14]; %velocidad 
hold on
plot(hM,vM,'bo','markersize',3,'markerfacecolor','b')

L=50.5; %longitud del tubo 3 en cm
D=5.36;  %diámetro del tubo 3 en mm

h=0.05:0.01:0.4; %alturas
v=zeros(1,length(h));
hold on
%régimen turbulento
i=1;
for x=h
    f=@(v) (2.78*D^1.25/1000)*v^2.25+5.6222e-
4*L*v^2-(2*9.8*x*D^1.25/1000)*v^0.25;
    v(i)=fzero(f,[0.1,2]); %velocidades
    i=i+1;
end
plot(h,v)
%régimen laminar
i=1;
for x=h
    a=2.78*D^2/1000;
    b=64*L*1.002e-5;
    c=-2*9.8*x*D^2/1.0e3;
    v(i)=(-b+sqrt(b^2-4*a*c))/(2*a); %velocidades
    i=i+1;
end
plot(h,v)
hold off
legend('datos', 'turbulento', 'laminar','location','northwest')
xlabel('h (m)')
ylabel('v (m/s)')
grid on
title('Tubo 3')

Actividades

Se elige uno de los tres tubos horizontales activando el botón de radio 1, 2, ó 3 del grupo titulado Tubo de vidrio
Se establece la altura h del extremo inferior del tubo vertical en el frasco Mariotte, en el contro titulado Altura del tubo

Se pulsa el botón titulado Nuevo y a cotinuación ►.

Se pulsa el botón titulado .

Se representa una porción del tubo horizontal ampliada, y una línea de corriente, una línea horizontal indica que el flujo es laminar, una línea quebrada señala que el flujo es turbulento.

El programa interactivo calcula la velocidad v del fluido en el tubo horizontal para cada altura h y el número de Reynolds.

Experiencia

Se establece la altura h del extremo inferior del tubo vertical en el frasco Mariotte medida desde el centro del orificio de salida, o desde el eje del tubo horizontal.

El agua que sale por el extremo del tubo horizontal cae en un medidor de caudal. El volumen de agua que sale del tubo horizontal en la unidad de tiempo (gasto) es

$G = \frac{π D^{2}}{4} v$

Se mide el volumen V de agua en cm³ recogida en el medidor de caudal en el tiempo t, V=G·t. Conocido el diámetro del tubo se calcula la velocidad v de salida del agua.

Si empleamos el tercer tubo D=5.36 mm y se ha tardado t=8.89 s en recoger V=200 cm³. La velocidad v de salida del agua es

$\frac{200}{8.89} = π \frac{{0.536}^{2}}{4} v$

v=99.7 cm/s =1.0 m/s

El número de Reynolds se calcula mediante la fórmula

$R = \frac{ρ D v}{η} = \frac{1000 \cdot 5.36 \cdot 10^{- 3} \cdot 1.0}{1.002 \cdot 10^{- 3}} = 5349$

Tubo de vidrio: Longitud Diámetro:
Altura del tubo

Referencias

Maroto, J. A, de Dios J., de las Nieves F. J. Utilización de un frasco de Mariotte para el estudio experimental de la transición de régimen laminar a turbulento. Revista Española de Física, Vol-13, nº 5, págs 42-47.(1999)