Caída de un columna vertical de fluido

Se dispone de tubos de vidrio de 1.6 m de longitud y cuyos radios pueden variar entre 0.1 y 0.5 mm. Se coloca el tubo verticalmente sobre un recipiente que contiene el líquido, tal como se muestra en la figura. Se succiona el líquido que asciende hacia arriba y cuando llega a una determinada altura se tapa el extremo superior con un dedo, mientras el otro extremo permanece en el depósito.

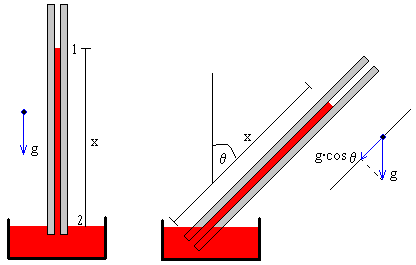
Se retira el dedo que obstruye la entrada de aire por el extremo superior, se pone en marcha un cronómetro y se mide el tiempo que tarda el líquido en caer una distancia x.

Cuando un líquido fluye por un capilar de radio R, con velocidad (media) v. La ley de Poiseuille afirma que el gasto G= πR²v es proporcional al gradiente de presión (p₁-p₂)/L entre dos posiciones 1 y 2 del capilar que distan L.

${\displaystyle G=\frac{\pi R^4}{8\eta }\frac{(p_1-p_2)}{L}}$

Si en un instante t la altura del líquido en el tubo vertical es x. La diferencia de presión p₁-p₂=ρgx debida a la altura de la columna de fluido en el tubo, mueve a la columna de fluido de longitud L=x con velocidad v.

${\displaystyle \pi R^{2}v=\frac{\pi R^4}{8\eta }\frac{\rho gx}{x}v=\frac{\rho R^2}{8\eta }g}$

Siendo ρ la densidad del fluido

Si inclinamos la varilla un ángulo θ, la diferencia de presión disminuye,

p₁-p₂=ρg(cosθ)x

y la velocidad constante de caída del fluido v vale

${\displaystyle v=\frac{\rho R^2}{8\eta }g\cos \theta }$

Los valores de la densidad ρ de los líquidos analizados se proporcionan en la siguiente tabla

Fuente: Koshkin N. I., Shirkévich M. G. Manual de Física Elemental. Editorial Mir (1975). pág. 37

Ejemplo

• Se elige agua, densidad, ρ=1000 kg/m³

• Se inclina el tubo θ=60º

• Se elige el tubo de radio R=0.2 mm

La columna de agua en el tubo se desplaza 1 m en 42.75 s.

${\displaystyle v=\frac{\rho R^2}{8\eta }g\cos \theta \frac{\text{1}\text{.0}}{\text{42}\text{.75}}=\frac{1000·{0.0002}^2}{8\eta }9.8\cos 60º\eta =1.05·{10}^{-3}\text{kg/(m·s)}}$

Actividades

Se introduce

• El ángulo θ que forma el tubo con la dirección vertical, en el control titulado Ángulo.

• El líquido, en el control titulado Líquido

• El radio R del capilar en mm, en el control titulado Radio

Se pulsa el botón titulado Nuevo

Se mide el tiempo que tarda la columna de líquido en caer una cierta altura, por ejemplo, 1.5 m.

El dato del tiempo en segundos y la posición del extremo de la columna de líquido, se proporciona en la parte superior derecha.

Se despeja la viscosidad

Desplazamiento de una burbuja de aire en un tubo capilar

Se dispone horizontalmente un largo tubo de vidrio (capilar) de pequeño diámetro y longitud L.  Los extremos A y B del tubo se conectan a dos recipientes grandes. Se llena el dispositivo con el líquido cuya viscosidad se desea medir de modo que una burbuja de aire permanezca en su interior del tubo horizontal.

Sea h la diferencia de las alturas entre los niveles de líquido en los dos depósitos. Cuando se abren simultáneamente las llaves en los extremos de los depósitos, la burbuja tiende a moverse a lo largo del tubo horizontal con velocidad constante v. Vamos a relacionar la diferencia de alturas h con la velocidad v con la que se desplaza de la burbuja de aire en el tubo horizontal.

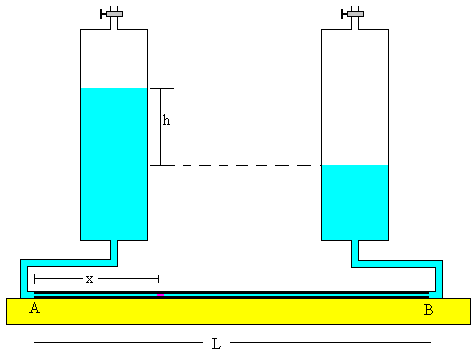
La diferencia de presión entre los extremos  del tubo horizontal es

p_A-p_B=ρgh

Supongamos que la longitud del tubo es L y la longitud de la burbuja es d<<L

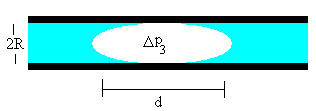
La diferencia de presión p_A-p_B cuando la burbuja está en movimiento comprende de tres partes:

1. Movimiento del líquido

La ley de Poiseuille afirma que el gasto G= πR²v es proporcional a la diferencia de presión. Como hay líquido en la porción L-d del tubo y el fluido se mueve con velocidad (media) v.

${\displaystyle \Delta p_1=\frac{8\eta (L-d)}{\pi R^4}G=\frac{8\eta (L-d)}{\pi R^4}\pi R^{2}v=\frac{8\eta (L-d)}{R^2}v}$

Siendo η la viscosidad desconocida del fluido

2. Movimiento del aire de la burbuja

De modo análogo, aplicamos la ley de Poiseuille a la porción aire en el interior de la burbuja de longitud d, que se desplaza con velocidad v por el interior del tubo.

${\displaystyle \Delta p_2=\frac{8\eta \text{'}d}{R^2}v}$

Siendo η’=1.72·10^-5 kg/(m·s) la viscosidad del aire

3. El exceso de presión en el interior de la burbuja de aire.

El exceso de presión en una burbuja esférica de radio R en el interior de un líquido de tensión superficial γ es

${\displaystyle \Delta p_3=\frac{2\gamma }{R}}$

Cuando la burbuja no es esférica, sino de la forma mostrada en la figura, la expresión es

${\displaystyle \Delta p_3=\frac{2\gamma }{R}(\cos {\theta }_1-\cos {\theta }_2)}$

donde θ₁ y θ₂ son los ángulos de contacto (véase el segundo artículo citado en las referencias).

La diferencia de presión p_A-p_B entre los extremos del tubo horizontal es

${\displaystyle \begin{array}{l}{p}_A-p_B=\Delta p_1+\Delta p_2+\Delta p_3\\ \rho gh=\frac{8v}{R^2}\left(d\eta \text{'}+(L-d)\eta \right)+\Delta p_3\end{array}}$

Dado que la viscosidad del aire η’ es muy pequeña, del orden de 10^-5 comparada con la viscosidad η de un líquido como el agua del orden de 10^-3 y por otra parte, la longitud de la burbuja de aire d es del orden de 1 cm frente a L que es del orden de un metro, podemos despreciar el término Δp₂ frente a las otras contribuciones.

${\displaystyle \begin{array}{l}\rho gh=\frac{8v}{R^2}(L-d)\eta +\Delta p_3\\ h=\frac{8(L-d)\eta }{\rho g{R}^2}v+\frac{\Delta p_3}{\rho g}\end{array}}$

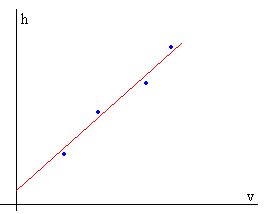
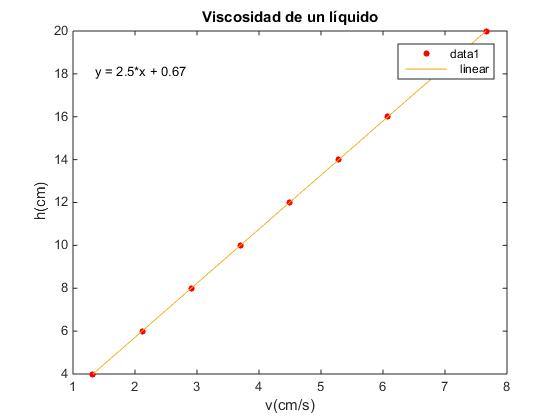
Cuando representamos la diferencia de presión h en cm de líquido en el eje Y y la velocidad v en cm/s en el eje X obtenemos una línea recta cuya pendiente es proporcional a la viscosidad y cuya ordenada en el origen es el exceso Δp₃/(ρg) de presión en el interior de la burbuja de aire debido a la tensión superficial del líquido.

Nota: a medida que la burbuja se desplaza en el tubo horizontal, pasa una cantidad pequeña de líquido del depósito izquierdo al derecho. Como el radio del tubo es muy pequeño y los depósitos tienen sección grande, la variación de altura es despreciable, es decir, h se mantiene prácticamente constante durante la medida.

Actividades

• Se elige el líquido en el control titulado Líquido

• Se establece la diferencia p_A-p_B=ρgh de presión en cm de líquido, en el control titulado Presión.

Se pulsa el botón titulado Nuevo y a continuación, ►

Se abre la llave que permite que el aire entre en el depósito de la izquierda y la burbuja se desplace por el capilar impulsada por la diferencia de presión entre los dos recipientes.

Se han fijado los siguientes parámetros:

• El radio del tubo horizontal, R=0.058 cm

• La longitud del tubo horizontal, L=100 cm

• La longitud de la burbuja de aire, d=1 cm

Datos de la densidad de los líquidos

Se mide la velocidad de la burbuja de aire dividiendo el desplazamiento L=100 cm entre el tiempo que tarda en desplazarse

Se cambia la presión, es decir, la diferencia de alturas h entre niveles de líquido en los dos depósitos y se mide la velocidad v de desplazamiento de la burbuja.

Se representa la recta

${\displaystyle h=\frac{8(L-d)\eta }{\rho g{R}^2}v+\frac{\Delta p_3}{\rho g}}$

y los datos “experimentales” en forma de puntos.

Calculamos la pendiente de la recta que mejor ajusta. A partir de este dato, se determina la viscosidad η del fluido

Ejemplo:

Elegimos el agua, se realizan varias medidas

>> t=[75.67,47.30,34.40,27.03,22.26,18.92,16.45,14.55,13.05];
>> h=4:2:20;
>> v=100./t;
>> plot(v,h,'ro','markersize',4,'markerfacecolor','r')
>> xlabel('v(cm/s)')
>> ylabel('h(cm)')
>> grid on
>> title('Viscosidad de un líquido')

Aparece la ventana gráfica. En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.

La pendiente de la recta es 2.52 s

${\displaystyle 2.52=\frac{8·(1.0-0.01)·\eta }{1000·9.8·\text{0}{\text{.00058}}^2}\eta =1.05·{10}^{-3}\text{kg/(m·s)}}$

Referencias

Peiris M. G. C., Tennakone K. Simple method for determination of the viscosity of a liquid. Am. J. Phys. 48 (6) June 1980, pp- 497-498

Elkarim A. A., A new type of viscosimeter. Am. J. Phys. 16 (9) December 1948, pp. 489-490