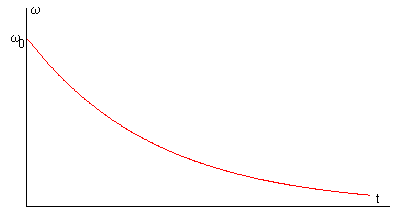
El efecto de la viscosidad del gas sobre un disco en rotación es su velocidad angular disminuya de forma exponencial con el tiempo

ω=ω₀·exp(-k·t)

En esta página se simula una experiencia que mide la viscosidad de un gas observando la disminución de la velocidad angular de rotación de un disco.

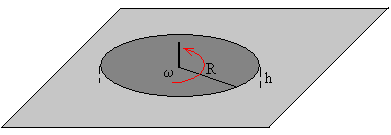
El dispositivo experimental consta de un disco de radio R, que puede girar alrededor de un eje vertical con un rozamiento muy pequeño en los rodamientos. El disco de masa m está suspendido por la presión del gas a una altura h (muy pequeña) por encima de una superficie plana.

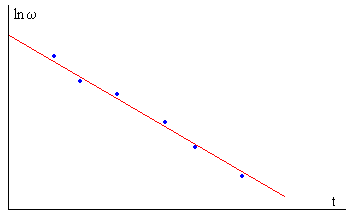
Se le proporciona al disco una velocidad angular inicial ω₀, se mide la velocidad angular ω en función del tiempo t, representándose en el eje vertical el logaritmo neperiano de la velocidad angular, ln(ω) y en el eje horizontal el tiempo t. Se obtiene una recta. A partir de la pendiente de la recta, calculamos la viscosidad del gas.

El coeficiente de viscosidad está relacionado con la distribución de velocidades en las capas de fluido situadas entre dos superficies en movimiento relativo. Las velocidades de estas capas tienen que ser menores que la velocidad media de las moléculas del gas, que es mayor que 500 m/s a temperatura ambiente, 293ºK .

Al estudiar el concepto de viscosidad, vimos que la fuerza por unidad de área era proporcional al gradiente de velocidad, la constante de proporcionalidad se denomina coeficiente de viscosidad η

${\displaystyle \frac{F}{A}=\eta \frac{dv}{dx}}$

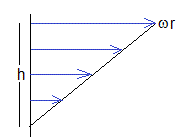
En un instante t, el disco gira con velocidad angular ω. Consideremos el gas contenido en la capa cilíndrica de radio r, espesor dr y altura h. El gas que está cerca de la placa horizontal tiene velocidad cero y el gas que está próximo al disco, lleva una velocidad v=ωr y en la superficie plana la velocidad es nula.

El perfil de velocidades se muestra en la figura, por lo que d(ωr)/dx=ωr/h

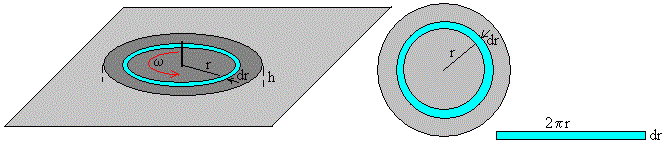
El área del anillo de radio r y espesor dr es 2πr·dr. El gradiente de velocidad es ωr/h

La definición de viscosidad se expresa en este caso,

${\displaystyle \frac{dF}{2\pi r·dr}=\eta \frac{\omega r}{h}dF=\eta \frac{2\pi r^2\omega }{h}dr}$

El momento de esta fuerza respecto del eje de rotación es

dM=r·dF

El momento total de las fuerzas que ejerce el gas sobre cada uno de los anillos en los que se ha dividido el disco es

${\displaystyle M={\displaystyle \underset{0}{\overset{R}{\int }}\eta \frac{2\pi r^3\omega }{h}dr}=\eta \frac{\pi R^4}{2h}\omega }$

Este momento se opone a la rotación del disco. La ecuación de la dinámica de rotación es

Idω/dt=-M

El momento de inercia I de un disco respecto de un eje perpendicular al disco y que pasa por su centro es I=mR²/2

${\displaystyle \begin{array}{l}\frac{d\omega }{dt}=-\eta \frac{\pi R^2}{mh}\omega \\ {\displaystyle \underset{{\omega }_0}{\overset{\omega }{\int }}\frac{d\omega }{\omega }}=-\eta \frac{\pi R^2}{mh}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\end{array}}$

donde ω₀ es la velocidad angular inicial, en el instante t=0.

${\displaystyle \omega ={\omega }_0\exp (-k·t)k=\eta \frac{\pi R^2}{mh}}$

La velocidad angular de rotación disminuye exponencialmente con el tiempo

Tal como se afirma en el artículo citado en lasreferencias, la medida de la pequeña distancia h entre el disco y la placa horizontal se realiza de forma indirecta a través de la medida de la capacidad C del condensador formado por el disco y el plano

${\displaystyle C=\frac{{\epsilon }_0\pi R^2}{h}}$

Actividades

• Se selecciona el gas, cuya viscosidad se desea medir, en el control de titulado Gas.

• La masa del disco se ha fijado en m=1.3 kg.

• El radio del disco, R=6.25 cm

• La distancia entre el disco y el plano horizontal en h=0.16 mm

• La velocidad angular inicial de rotación del disco ω₀=6.0 rad/s

Se pulsa el botón titulado Nuevo

Se observa el disco en rotación. En la parte superior, se representa:

• En el eje horizontal, el tiempo t en minutos

• En el eje vertical, ln(ω)

Calculamos la pendiente, k, obtenemos el valor de la viscosidad η del gas seleccionado.

Los valores de la viscosidad de los gases estudiados se han tomado del artículo citado en las referencias.

Ejemplo.

Se selecciona Hidrógeno

En el instante t=8 min, ln(ω)=1.54

O bien, en el instante t=480 s, ω=4.67 rad/s

${\displaystyle \begin{array}{l}k=\frac{\ln ({\omega }_0)-\ln (\omega )}{t}=\frac{\ln (6.0)-1.54}{480}=5.24·{10}^{-4}{\text{s}}^{\text{-1}}\\ k=\eta \frac{\pi R^2}{mh}\eta =\frac{1.3·0.16·{10}^{-3}·5.24·{10}^{-4}}{\pi {(0.0625)}^2}=8.89·{10}^{-6}\text{kg/(m·s)}\end{array}}$

Referencias

Nienart L., Measuring the viscosity of gases. Am. J. Phys. 62 (6) June 1994, pp. 566-568