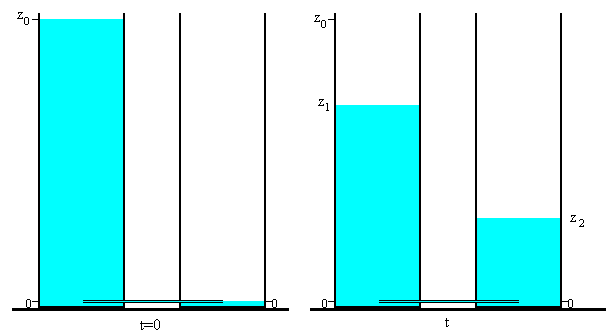
En la figura se muestran los dos depósitos iguales, de sección A, unidos por un tubo capilar de radio R y longitud L. El líquido tiene viscosidad η. En el instante t=0, el depósito de la izquierda está lleno hasta una altura z₁=z₀ y el de la derecha vacío z₂=0. Vamos a determinar la altura z₁ del líquido en el depósito izquierdo en función del tiempo t.

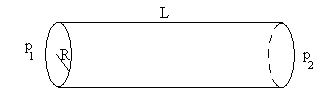
La ley de Poiseuille afirma que la cantidad de fluido de viscosidad η que atraviesa en la unidad de tiempo (gasto) la sección de un tubo de radio R y longitud L cuando está sometido a una diferencia de presión p₁-p₂ en sus extremos es

${\displaystyle G=\frac{\pi (p_1-p_2)R^4}{8L\eta }}$

Puesto que el movimiento del líquido en los dos recipientes es muy lento, podemos considerar que las presiones p₁ y p₂ en los extremos del tubo capilar son aproximadamente, las presiones hidrostáticas:

p₁=p₀+ρgz₁
p₂=p₀+ρgz₂

debidas a las alturas de fluido z₁ y z₂ en los respectivos depósitos. p₀ es la presión atmosférica.

Del depósito de la izquierda sale una cantidad G de fluido en la unidad de tiempo, como consecuencia la altura del fluido en el depósito de sección A disminuye

${\displaystyle G=-A\frac{d{z}_1}{dt}}$

Como la cantidad de fluido que sale del depósito de la izquierda es igual al que entra en el depósito de la derecha y ambos tiene la misma sección, la relación de alturas es 

${\displaystyle \begin{array}{l}A\frac{d{z}_1}{dt}=-\frac{\pi \rho g{R}^4}{8L\eta }(2z_1-z_0)\\ \frac{d{z}_1}{dt}=-\frac{\pi \rho g{R}^4}{8AL\eta }(2z_1-z_0)\\ \frac{d{z}_1}{dt}=-K(2z_1-z_0)\end{array}}$

Se integra esta ecuación diferencial con las condiciones iniciales siguientes: en el instante t=0, la altura del líquido es z₀

${\displaystyle \begin{array}{l}{\displaystyle \underset{z_0}{\overset{z_1}{\int }}\frac{d{z}_1}{2z_1-z_0}}={\displaystyle \underset{0}{\overset{t}{\int }}-K·dt}\\ {\frac{1}{2}\ln (2z_1-z_0)|}_{z_0}^{z_1}=-Kt\\ z_1=\frac{z_0}{2}\left(1+\exp (-2Kt)\right)\end{array}}$

Después de un tiempo suficientemente grande, t→∞, la altura del líquido en cada depósito es z₀/2

Variación de la viscosidad del agua con la temperatura

En la siguiente tabla se proporcionan los datos de la viscosidad del agua en mPa·s a diversas temperaturas.

Fuente: Koshkin N. I., Shirkévich M. G.. Manual de Física Elemental. Editorial Mir 1975

La viscosidad η varía con la temperatura absoluta T de la forma

${\displaystyle \eta =b·\exp \left(\frac{a}{T}\right)}$

siendo a y b constantes características de cada líquido en particular

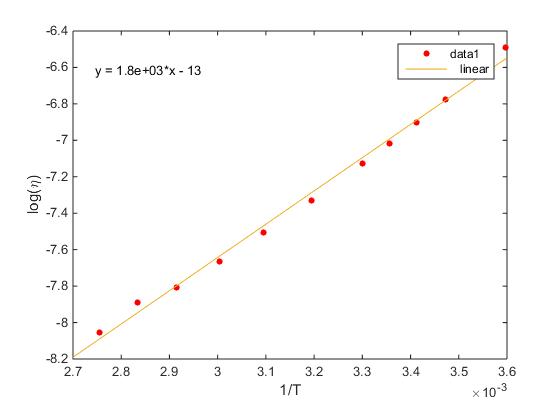
Estas constantes se puede calcular, mediante el procedimiento de regresión lineal, las abscisas son las inversas de la temperaturas absoluta 1/(t+273) y las ordenadas son los logaritmos neperianos de la viscosidad lnη. La pendiente de la recta de ajuste es el parámetro a y la ordenada en el origen lnb.

${\displaystyle \ln \eta =\ln b+\frac{a}{T}}$

>> t=[5,10,15,20,25,30,40,50,60,70,80,90]+273;
>> plot(1./t,log(x),'ro','markersize',4,'markerfacecolor','r')
>> xlabel('1/T')
>> ylabel('log(\eta)')

Aparece la ventana gráfica. En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.

Los valores obtenidos son a=1825.5 y b=exp(-13.119)=2.0067·10^-6

Actividades

Se pulsa el botón titulado Nuevo

• Se establece la temperatura del agua, en el control titulado Temperatura
• Se elige el diámetro del tubo capilar D, en el control titulado Diámetro capilar

Se han fijado en el programa:

• Diámetro de la sección de los depósitos cilíndricos, 15 cm, su área es A=π(0.075)²
• Altura inicial del agua, z₀=50 cm en el depósito de la izquierda, el de la derecha está inicialmente vacío.
• Longitud del tubo capilar, L=25 cm

Se pulsa el botón titulado Nuevo

Observamos como desciende la altura del agua en el depósito de la izquierda y aumenta en el de la derecha.

Ejemplo:

• Diámetro de la sección de los depósitos cilíndricos, 15 cm
• Altura inicial del agua, z₀=50 cm
• Longitud del tubo capilar, L=25 cm
• Diámetro del tubo capilar, D=0.9 mm
• Temperatura del agua, 20ºC

Determinar la viscosidad del agua a dicha temperatura

La altura del agua en el depósito de la izquierda z₁ en función del tiempo t es

${\displaystyle z_1=\frac{z_0}{2}\left(1+\exp (-2Kt)\right)}$

o bien,

${\displaystyle -\ln \left(\frac{2z_1}{z_0}-1\right)=2Kt}$

Se toman los datos del tiempo t en segundos y de la altura z₁ en cm

Si en el eje X representamos los tiempos t, y en el eje Y $-\ln \left(\frac{2z_1}{z_0}-1\right)$ obtenemos una recta de pendiente 2K

>> t=[0,3192,7268,13024,22908];
>> z1=50:-5:30;
>> plot(t,-log(2*z1/50-1),'ro','markersize',4,'markerfacecolor','r')
>> xlabel('t(s)')
>> ylabel('-log(2z_1/z_0-1)')
>> title('Viscosidad del agua a 20º C')

Aparece la ventana gráfica. En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.

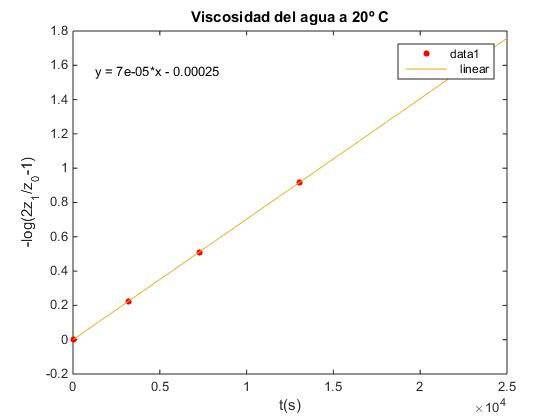
Conocida la pendiente de la recta 2K=7.032·10^-5, calculamos la viscosidad del agua a la temperatura seleccionada

${\displaystyle \begin{array}{l}K=\frac{\pi \rho g{R}^4}{8AL\eta }\\ \eta =\frac{\pi \rho g{R}^4}{8ALK}\eta =\frac{\pi 1000·9.8{\left(0.9·{10}^{-3}/2\right)}^4}{8\pi {\left(0.15/2\right)}^{2}0.25(7.032·{10}^{-5}/2)}=1.016·{10}^{-3}\text{Pa}=1.016\text{mPa}\end{array}}$

En este experimento simulado, se supondrá que el fluido está en todo momento en régimen laminar y también, que el movimiento del fluido en los depósitos es lento.

Referencias

Ortega F. M., Pavioni O.D., Domínguez H. L., A communicating-vessel viscosimeter. The Physics Teacher 45, February 2007, pp. 116-118