Empezamos con las ecuaciones de Navier-Stokes en coordenadas rectangulares en dos dimensiones

${\displaystyle \begin{array}{l}\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}=0\\ \{\begin{array}{l}{\rho }_f\left(\frac{\partial u_x}{\partial t}+u_x\frac{\partial u_x}{\partial x}+u_y\frac{\partial u_x}{\partial y}\right)=-\frac{\partial p}{\partial x}+{\rho }_f{g}_x+\eta \left(\frac{{\partial }^2{u}_x}{\partial x^2}+\frac{{\partial }^2{u}_x}{\partial y^2}\right)\\ {\rho }_f\left(\frac{\partial u_y}{\partial t}+u_x\frac{\partial u_y}{\partial x}+u_y\frac{\partial u_y}{\partial y}\right)=-\frac{\partial p}{\partial y}+{\rho }_f{g}_y+\eta \left(\frac{{\partial }^2{u}_y}{\partial x^2}+\frac{{\partial }^2{u}_y}{\partial y^2}\right)\end{array}\end{array}}$

Fluido sobre una placa plana

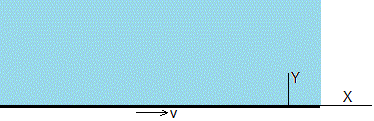
Una placa indefinida soporta un fluido de altura infinita. En el instante inicial t=0, se pone en movimiento con velocidad v cuya dirección es el eje X. Vamos a determinar como evlouciona el perfil u_x(y, t) de velocidades del fluido

Como la componente u_y y sus derivadas son nulas, las ecuaciones de Navier-Stokes se simplifican

${\displaystyle \begin{array}{l}\frac{\partial u_x}{\partial x}=0\\ \{\begin{array}{l}{\rho }_f\frac{\partial u_x}{\partial t}=\eta \frac{{\partial }^2{u}_x}{\partial y^2}\\ 0=-\frac{\partial p}{\partial y}+{\rho }_{f}g\end{array}\end{array}}$

La ecuación de continuidad nos indica que u_x no depende de x. La presión p no depende de x

Resolvemos la ecuación diferencial

${\displaystyle \frac{\partial u_x}{\partial t}=\upsilon \frac{{\partial }^2{u}_x}{\partial y^2},\upsilon =\frac{\eta }{{\rho }_f}}$

Con las condiciones iniciales, en el instante t=0, u_x(y)=0, 0≤y<∞. El fluido parte del reposo

y las condiciones de contorno para t>0

• u_x(0, t)=v en y=0
• u_x(∞, t)=0 en y=∞

Haciendo el cambio de variable

${\displaystyle \begin{array}{l}z=\frac{y}{2\sqrt{\upsilon t}}\\ \frac{\partial u_x}{\partial y}=\frac{\partial u_x}{\partial z}\frac{\partial z}{\partial y}=\frac{\partial u_x}{\partial z}\frac{1}{2\sqrt{\upsilon t}}\\ \frac{{\partial }^2{u}_x}{\partial y^2}=\frac{\partial }{\partial y}\left(\frac{\partial u_x}{\partial y}\right)=\frac{\partial }{\partial z}\left(\frac{\partial u_x}{\partial z}\frac{1}{2\sqrt{\upsilon t}}\right)\frac{\partial z}{\partial y}=\frac{1}{4\upsilon t}\frac{{\partial }^2{u}_x}{\partial z^2}\\ \frac{\partial u_x}{\partial t}=\frac{\partial u_x}{\partial z}\frac{\partial z}{\partial t}=-\frac{y}{4t\sqrt{\upsilon t}}\frac{\partial u_x}{\partial z}=-\frac{z}{2t}\frac{\partial u_x}{\partial z}\end{array}}$

Sustituyendo en la ecuación diferencial

${\displaystyle \frac{{\partial }^2{u}_x}{\partial z^2}+2z\frac{\partial u_x}{\partial z}=0}$

Integramos la derivada primera s de u_x

${\displaystyle \begin{array}{l}s=\frac{d{u}_x}{dz}\\ \frac{ds}{dz}+2zs=0\\ \frac{ds}{s}=-2z·dz\\ \ln s=-z^2+\ln c_1\\ \ln \frac{s}{c_1}=-z^2\\ \frac{d{u}_x}{dz}=c_1\exp \left(-z^2\right)\end{array}}$

Integramos de nuevo, sabiendo que para y=0, u_x=v

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{u_x}{\int }}d{u}_x=c_1{\displaystyle \underset{0}{\overset{z}{\int }}\exp \left(-z^2\right)dz}}\\ u_x-v=c_1{\displaystyle \underset{0}{\overset{z}{\int }}\exp \left(-z^2\right)dz}\end{array}}$

Determinamos la constante c₁ con la condición de contorno y→∞, u_x→0

${\displaystyle \begin{array}{l}0-v=c_1{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-z^2\right)dz}\\ -v=c_1\frac{\sqrt{\pi }}{2},c_1=-v\frac{2}{\sqrt{\pi }}\\ u_x=v\left(1-\frac{2}{\sqrt{\pi }}{\displaystyle \underset{0}{\overset{z}{\int }}\exp \left(-z^2\right)dz}\right)=v\left(1-\text{erf(z)}\right)=v·\text{erfc}\left(\frac{y}{2\sqrt{\upsilon t}}\right)\end{array}}$

erf es la función error. Al final de la página titulada Integrales se justifica el resultado de la integral exp(-z²) entre 0 e ∞

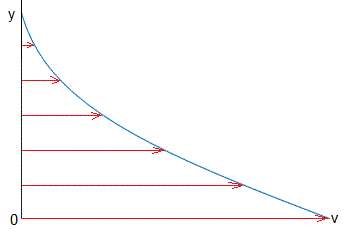
El perfil de velocidades en el instante t es

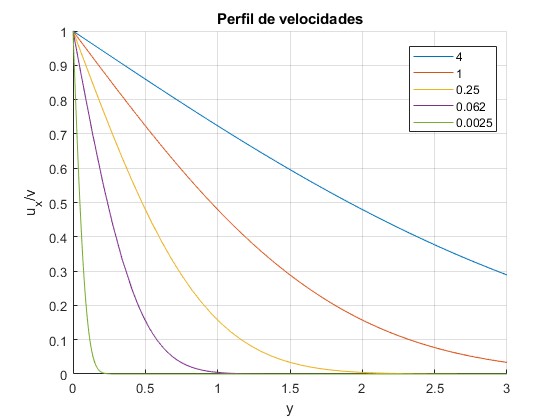
Representamos el perfil las velocidades de u_x/v para los instantes k=tν=4,1,0.25, 0.062, 0.0025

old on
for k=[4,1,0.25,0.062, 0.0025]
    fplot(@(y) erfc(y/(2*sqrt(k))),[0,3],'displayName',num2str(k))
end
hold off
grid on
legend('-DynamicLegend','location','best')
xlabel('y')
ylabel('u_x/v')
title('Perfil de velocidades')

Placa oscilante

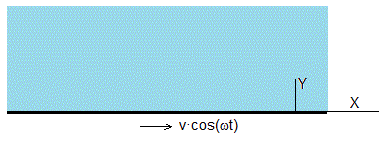
Una placa indefinida soporta un fluido de altura infinita. En el instante inicial t=0, se pone en movimiento oscilatorio con velocidad vcos(ωt) cuya dirección es el eje X. Vamos a determinar como evlouciona el perfil u_x(y, t) de velocidades del fluido

Resolvemos la ecuación diferencial

${\displaystyle \frac{\partial u_x}{\partial t}=\upsilon \frac{{\partial }^2{u}_x}{\partial y^2},\upsilon =\frac{\eta }{{\rho }_f}}$

con las condiciones de contorno siguientes

${\displaystyle \{\begin{array}{l}{u}_x(\mathrm{0,}t)=v\cos \left(\omega t\right),y=\mathrm{0,}t>0\\ u_x(\infty ,t)=\mathrm{0,}y=\infty ,t\ge 0\end{array}}$

Probamos una solución de variables separadas, una que depende de y y otra del tiempo t

${\displaystyle u_x(y,t)=\Re \left[Y(y)\exp \left(i\omega t\right)\right]}$

El símbolo $\Re$, indica la parte real del número complejo

Introducimos la solución en la ecuación diferencial en derivadas parciales, obtenemos una ecuación diferencial en Y(y) cuya solución es

${\displaystyle \begin{array}{l}\frac{d^{2}Y}{d{y}^2}-\frac{i\omega }{\upsilon }Y=0\\ Y(y)=c_1\exp \left(\sqrt{\frac{i\omega }{\upsilon }}y\right)+c_2\exp \left(-\sqrt{\frac{i\omega }{\upsilon }}y\right)\end{array}}$

Los coeficientes c₁ y c₂ se determinan a partir de las condiciones de contorno.

Cuando y→∞, Y(y)→∞, por lo que c₁ tiene que ser cero

${\displaystyle \begin{array}{l}Y(y)=c_2\exp \left(-\sqrt{\frac{i\omega }{\upsilon }}y\right)\\ \sqrt{i}=\exp \left(i\frac{\pi }{4}\right)=\frac{1}{\sqrt{2}}\left(1+i\right)\\ Y(y)=c_2\exp \left(-\sqrt{\frac{\omega }{2\upsilon }}\left(1+i\right)y\right)\end{array}}$

La solución de la ecuación diferencial en derivadas parciales es

${\displaystyle \begin{array}{l}{u}_x(y,t)=ℝ\left[c_2\exp \left(-\sqrt{\frac{\omega }{2\upsilon }}\left(1+i\right)y\right)\exp \left(i\omega t\right)\right]=\\ c_2\Re \left[\exp \left(-\sqrt{\frac{\omega }{2\upsilon }}y\right)\exp \left(i\left(\omega t-\sqrt{\frac{\omega }{2\upsilon }}y\right)\right)\right]=c_2\exp \left(-\sqrt{\frac{\omega }{2\upsilon }}y\right)\cos \left(\omega t-\sqrt{\frac{\omega }{2\upsilon }}y\right)\end{array}}$

La condición de contorno en y=0 determina el coeficiente c₂

${\displaystyle \begin{array}{l}{u}_x(\mathrm{0,}t)=v\cos \left(\omega t\right)=c_2\cos \left(\omega t\right)\\ c_2=v\\ u_x(y,t)=v\exp \left(-\sqrt{\frac{\omega }{2\upsilon }}y\right)\cos \left(\omega t-\sqrt{\frac{\omega }{2\upsilon }}y\right)\end{array}}$

Se trata de la ecuación de un movimiento ondulatorio armónico

• Cuya amplitud decrece exponencialmente con y

${\displaystyle v\exp \left(-\sqrt{\frac{\omega }{2\upsilon }}y\right)}$

• De longitud de onda

${\displaystyle \lambda =\frac{2\pi }{\sqrt{\frac{\omega }{2\upsilon }}}=2\pi \sqrt{\frac{2\upsilon }{\omega }}}$

• La velocidad de propagación (velocidad de fase)

${\displaystyle \begin{array}{l}\sqrt{\frac{\omega }{2\upsilon }}{v}_p=\omega \\ v_p=\sqrt{2\upsilon \omega }\end{array}}$

Actividades

Se pulsa el botón titulado Nuevo para observar cómo cambia el perfil de velocidades con el tiempo

Fluido entre dos placas planas y paralelas (I)

Situamos el fluido entre dos placas planas y paralelas, distantes h. En el instante t=0, la placa inferior se pone en movimiento con velocidad V cuya dirección es el eje X

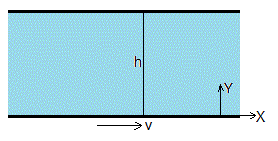
Resolvemos la ecuación diferencial

${\displaystyle \frac{\partial u_x}{\partial t}=\upsilon \frac{{\partial }^2{u}_x}{\partial y^2},\upsilon =\frac{\eta }{{\rho }_f}}$

Con las condiciones iniciales, en el instante t=0, u_x(y,0)=0, 0≤y≤h. El fluido parte del reposo

y las condiciones de contorno para t>0

• u_x(0, t)=V en y=0
• u_x(h, t)=0 en y=h

Ya hemos estudiado la solución en el estado estacionario, que repetimos

Estado estacionario

${\displaystyle \frac{{\partial }^2{u}_x}{\partial y^2}=0}$

Integramos dos veces

${\displaystyle \begin{array}{l}\frac{\partial u_x}{\partial y}=c_1\\ u_x=c_{1}y+c_2\end{array}}$

Determinamos las constantes c₁ y c₂ con las condiciones de contorno

${\displaystyle \begin{array}{l}\{\begin{array}{l}v=c_2\\ 0=c_{1}h+c_2\end{array}\\ u_x(y,\infty )=-\frac{V}{h}y+V=V\left(1-\frac{y}{h}\right)\end{array}}$

El perfil de velocidades u_x(y) es lineal en el estado estacionario

El perfil de velocidades en el instante t, u_x(y,t) es la suma del perfil en el estado estacionario y en el estado transitorio

${\displaystyle u_x(y,t)=V\left(1-\frac{y}{h}\right)-u_x^t(y,t)}$

Introducimos esta expresión en la ecuación diferencial para obtener la correspondiente al estado transitorio

${\displaystyle \frac{\partial u_x^t}{\partial t}=\upsilon \frac{{\partial }^2{u}_x^t}{\partial y^2}}$

Resolvemos esta ecuación diferencial en derivadas paraciales con las condiciones de contorno e inicial, siguientes

${\displaystyle \begin{array}{l}\{\begin{array}{l}{u}_x^t(\mathrm{0,}t)=\mathrm{0,}y=\mathrm{0,}t>0\\ u_x^t(h,t)=\mathrm{0,}y=h,t\ge 0\end{array}\\ u_x^t(y\mathrm{,0})=V\left(1-\frac{y}{h}\right),0\le y\le h,t=0\end{array}}$

Variables separadas

Expresamos la solución de la ecuación diferencial como producto de dos funciones una que depende de la variable y y otra que depende de la variable t

${\displaystyle \begin{array}{l}{u}_x^t(y,t)=Y(y)T(t)\\ \frac{1}{\upsilon T}\frac{dT}{dt}=\frac{1}{Y}\frac{d^{2}Y}{d{y}^2}\end{array}}$

El miembro izquierdo, solamente depende de t y el derecho solamente de y. Transformamos una ecuación diferencial en derivadas parciales en un sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{1}{\upsilon T}\frac{dT}{dt}=-\frac{{\alpha }^2}{h^2}\\ \frac{1}{Y}\frac{d^{2}Y}{d{y}^2}=-\frac{{\alpha }^2}{h^2}\end{array}\\ \{\begin{array}{l}\frac{dT}{dt}+\frac{{\alpha }^2\upsilon }{h^2}T=0\\ \frac{d^{2}Y}{d{y}^2}+\frac{{\alpha }^2}{h^2}Y=0\end{array}\end{array}}$

Las soluciones de las ecuaciones diferenciales son

${\displaystyle \begin{array}{l}T(t)=c_0\exp \left(-\frac{{\alpha }^2\upsilon }{h^2}t\right)\\ Y(y)=c_1\sin \left(\frac{\alpha }{h}y\right)+c_2\cos \left(\frac{\alpha }{h}y\right)\end{array}}$

Los coeficientes c₁ y c₂ se determinan a partir de las condiciones de contorno

${\displaystyle \begin{array}{l}\{\begin{array}{l}{u}_x^t(\mathrm{0,}t)=Y(0)T(t)=\mathrm{0,}Y(0)=0\\ u_x^t(h,t)=Y(h)T(t)=\mathrm{0,}Y(h)=0\end{array}\\ c_2=\mathrm{0,}\sin \left(\frac{\alpha }{h}h\right)=\mathrm{0,}\alpha =k\pi ,k=\mathrm{1,2,...}\end{array}}$

La solución de la ecuación diferencial enderivadas parciales, es la superposición

${\displaystyle \begin{array}{l}{u}_x^t(y,t)={\displaystyle \sum _{k=1}^{\infty }{B}_k\sin \left({\alpha }_k\frac{y}{h}\right)}\exp \left(-\frac{{\alpha }_k^2}{h^2}\upsilon t\right)\\ u_x^t(y,t)={\displaystyle \sum _{k=1}^{\infty }{B}_k\sin \left(k\pi \frac{y}{h}\right)}\exp \left(-\frac{k^2{\pi }^2}{h^2}\upsilon t\right)\end{array}}$

Las constantes B_k se determinan a partir de la condición inicial

${\displaystyle \begin{array}{l}{u}_x^t(y\mathrm{,0})=V\left(1-\frac{y}{h}\right)\\ V\left(1-\frac{y}{h}\right)={\displaystyle \sum _{k=1}^{\infty }{B}_k\sin \left(k\pi \frac{y}{h}\right)}\end{array}}$

Teniendo en cuenta el resultado

${\displaystyle {\displaystyle \underset{0}{\overset{1}{\int }}\sin \left(m\pi x\right)}\sin \left(n\pi x\right)=\{\begin{array}{l}\frac{1}{2},m=n\\ \mathrm{0,}m\ne n\end{array}}$

>> syms m n z;
>> assume(m,'integer')
>> assume(n,'integer')
>> y=int(sin(m*pi*z)*sin(n*pi*z), z,0,1)
y =-(m*cos(pi*m)*sin(pi*n) - n*cos(pi*n)*sin(pi*m))/(pi*(m^2 - n^2))
>> limit(y,m,n)
ans =cos(pi*n)^2/2

Los coeficientes B_k

${\displaystyle {\displaystyle \sum _{k=1}^{\infty }{B}_k{\displaystyle \underset{0}{\overset{h}{\int }}\sin \left(k\pi \frac{y}{h}\right)\sin \left(n\pi \frac{y}{h}\right)}dy={\displaystyle \underset{0}{\overset{h}{\int }}V\left(1-\frac{y}{h}\right)\sin \left(n\pi \frac{y}{h}\right)dy}}}$

Resolvemos las integrales, haciendo el cambio de variable z=y/h. Integramos por partes la segunda

${\displaystyle \begin{array}{l}{B}_{k}h{\displaystyle \underset{0}{\overset{1}{\int }}{\sin }^2\left(k\pi z\right)}dz=Vh{\displaystyle \underset{0}{\overset{1}{\int }}\left(1-z\right)\sin \left(k\pi z\right)dz},\{\begin{array}{l}u=1-z,du=-dz\\ dv=\sin \left(k\pi z\right)dz,v=-\frac{\cos \left(k\pi z\right)}{k\pi }\end{array}\\ \frac{1}{2}{B}_k=V{\left\{-\frac{(1-z)\cos \left(k\pi z\right)}{k\pi }-\frac{\sin \left(k\pi z\right)}{k^2{\pi }^2}\right\}|}_0^1\\ B_k=\frac{2V}{k\pi }\end{array}}$

El resultado final es la suma del estado estacionario y el estado transitorio

${\displaystyle u_x(y,t)=V\left(1-\frac{y}{h}\right)-\frac{2V}{\pi }{\displaystyle \sum _{k=1}^{\infty }\frac{1}{k}\sin \left(k\pi \frac{y}{h}\right)}\exp \left(-\frac{k^2{\pi }^2}{h^2}\upsilon t\right)}$

Representamos u_x(y,t)/V en los instantes t=0.0001, 0.001, 0.01, 0.1, 1. Tomamos los 150 primeros términos del desarrollo en serie

yy=linspace(0,1, 200);
ux=zeros(length(yy),1);
hold on
for t=[0.0001,0.001 ,0.01,0.1,1]
    i=0;
    for y=yy
        i=i+1;
        ux(i)=1-y;
        for k=1:150
            ux(i)=ux(i)-2*sin(k*pi*y)*exp(-k^2*pi^2*t)/(pi*k);
        end
    end
    plot(ux,yy,'displayName',num2str(t))
end  
hold off
grid on
legend('-DynamicLegend','location','best')
xlabel('u_x/v')
ylabel('y/h')
title('Perfil de velocidades')

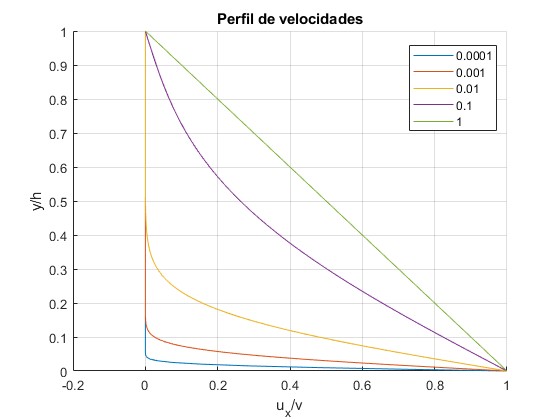
Para t=1, se ha establecido el perfil casi lineal de las velocidades del fluido, se está muy próximo al estado estacionario

Comparando esta figura con la de la primer apartado, vemos que la presencia del la plano paralelo en y=h no afecta al prefil de velocidades del fluido al principio

Actividades

Se pulsa el botón titulado Nuevo para observar el estado transitorio y su evolución hacia el estado estacionario

Fluido entre dos placas planas y paralelas (II)

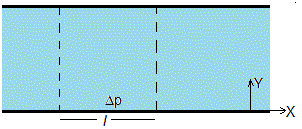
Situamos el fluido entre dos placas planas y paralelas, distantes h. En el instante t=0, se establece un gradiente de presión a lo largo del eje X,

${\displaystyle \frac{\partial p}{\partial x}=\frac{p_2-p_1}{x_2-x_1}=\frac{\Delta p}{l}}$

Para determinar el perfil de velocidades u_x(y,t), resolvemos la ecuación diferencial

${\displaystyle {\rho }_f\frac{\partial u_x}{\partial t}=-\frac{\Delta p}{l}+\eta \frac{{\partial }^2{u}_x}{\partial y^2}}$

Con las condicones de contorno e inicial

${\displaystyle \begin{array}{l}\{\begin{array}{l}{u}_x(\mathrm{0,}t)=\mathrm{0,}y=\mathrm{0,}t>0\\ u_x(h,t)=\mathrm{0,}y=h,t\ge 0\end{array}\\ u_x(y\mathrm{,0})=\mathrm{0,}0\le y\le h,t=0\end{array}}$

Estado estacionario

Integramos dos veces la ecuación diferencial

${\displaystyle \begin{array}{l}\eta \frac{{\partial }^2{u}_x}{\partial y^2}=\frac{\Delta p}{l}\\ u_x=\frac{1}{2}\frac{\Delta p}{\eta l}{y}^2+c_{1}y+c_2\end{array}}$

Aplicando la condición de contorno, u_x(0,t)=0, resulta c₂=0

Aplicando la condición de contorno, u_x(h, t)=0, resulta

${\displaystyle \begin{array}{l}0=\frac{1}{2}\frac{\Delta p}{\eta l}{h}^2+c_{1}h\\ c_1=-\frac{1}{2}\frac{\Delta p}{\eta l}h\\ u_x\left(y,\infty \right)=-\frac{1}{2}\frac{\Delta p}{\eta l}\left(h-y\right)y\end{array}}$

La solución de la ecuación diferencial en derivadas parciales u_x(y, t) es la suma del estado estacionario y del estado transitorio

${\displaystyle u_x(y,t)=-\frac{1}{2}\frac{\Delta p}{\eta l}\left(h-y\right)y+u_x^t(y,t)}$

Introducimos en la ecuación diferencial en derivadas parciales

${\displaystyle \begin{array}{l}{\rho }_f\frac{\partial u_x^t}{\partial t}=-\frac{\Delta p}{l}+\eta \left(\frac{{\partial }^2{u}_x^t}{\partial y^2}+\frac{\Delta p}{\eta l}\right)\\ \frac{\partial u_x^t}{\partial t}=\upsilon \frac{{\partial }^2{u}_x^t}{\partial y^2},\upsilon =\frac{\eta }{{\rho }_f}\end{array}}$

Con las condiciones de contorno e inicial

${\displaystyle \begin{array}{l}\{\begin{array}{l}{u}_x^t(\mathrm{0,}t)=\mathrm{0,}y=\mathrm{0,}t>0\\ u_x^t(h,t)=\mathrm{0,}y=h,t\ge 0\end{array}\\ u_x^t(y\mathrm{,0})=\frac{1}{2}\frac{\Delta p}{\eta l}\left(h-y\right)y,0\le y\le h,t=0\end{array}}$

La solución es similar al apartado anterior, variables separadas

${\displaystyle u_x^t(y,t)={\displaystyle \sum _{k=1}^{\infty }{B}_k\sin \left(k\pi \frac{y}{h}\right)}\exp \left(-\frac{k^2{\pi }^2}{h^2}\upsilon t\right)}$

Los coeficientes B_k se determinan a partir de la condición inicial

${\displaystyle \begin{array}{l}{u}_x^t(y\mathrm{,0})=\frac{1}{2}\frac{\Delta p}{\eta l}\left(h-y\right)y\\ \frac{1}{2}\frac{\Delta p}{\eta l}\left(h-y\right)y={\displaystyle \sum _{k=1}^{\infty }{B}_k\sin \left(k\pi \frac{y}{h}\right)}\end{array}}$

Teniendo en cuenta que

${\displaystyle {\displaystyle \underset{0}{\overset{1}{\int }}\sin \left(m\pi x\right)}\sin \left(n\pi x\right)=\{\begin{array}{l}\frac{1}{2},m=n\\ \mathrm{0,}m\ne n\end{array}}$

Calculamos los coeficientes B_k

${\displaystyle {\displaystyle \sum _{k=1}^{\infty }{B}_k{\displaystyle \underset{0}{\overset{h}{\int }}\sin \left(k\pi \frac{y}{h}\right)\sin \left(n\pi \frac{y}{h}\right)}dy={\displaystyle \underset{0}{\overset{h}{\int }}\frac{1}{2}\frac{\Delta p}{\eta l}\left(h-y\right)y\sin \left(n\pi \frac{y}{h}\right)dy}}}$

Se hace el cambio de variable z=y/h, y se integra dos veces por partes

${\displaystyle \begin{array}{l}{B}_{k}h{\displaystyle \underset{0}{\overset{1}{\int }}\sin \left(k\pi z\right)\sin \left(k\pi z\right)}dz=\frac{1}{2}\frac{\Delta p}{\eta l}{h}^2{\displaystyle \underset{0}{\overset{1}{\int }}\left(1-z\right)z\sin \left(k\pi z\right)dz}\\ \{\begin{array}{l}u=(1-z)z,du=(1-2z)dz\\ dv=\sin \left(k\pi z\right)dz,v=-\frac{\cos \left(k\pi z\right)}{k\pi }\end{array}\\ {\displaystyle \int \left(1-z\right)z\sin \left(k\pi z\right)dz}=-\frac{\left(1-z\right)z}{k\pi }\cos \left(k\pi z\right)+\frac{1}{k\pi }{\displaystyle \int \left(1-2z\right)\cos \left(k\pi z\right)dz}\\ \{\begin{array}{l}u=1-2z,du=-2dz\\ dv=\cos \left(k\pi z\right)dz,v=\frac{\sin \left(k\pi z\right)}{k\pi }\end{array}\\ -\frac{\left(1-z\right)z}{k\pi }\cos \left(k\pi z\right)+\frac{1}{k\pi }\left\{\frac{\left(1-2z\right)}{k\pi }\sin \left(k\pi z\right)+\frac{2}{k\pi }{\displaystyle \int \sin \left(k\pi z\right)dz}\right\}=\\ -\frac{\left(1-z\right)z}{k\pi }\cos \left(k\pi z\right)+\frac{1}{k\pi }\left\{\frac{\left(1-2z\right)}{k\pi }\sin \left(k\pi z\right)-\frac{2}{k^2{\pi }^2}\cos \left(k\pi z\right)\right\}\\ {\displaystyle \underset{0}{\overset{1}{\int }}\left(1-z\right)z\sin \left(k\pi z\right)dz}={-\left(\frac{\left(1-z\right)z}{k\pi }+\frac{2}{k^3{\pi }^3}\right)\cos \left(k\pi z\right)+\frac{\left(1-2z\right)}{k^2{\pi }^2}\sin \left(k\pi z\right)|}_0^1=\frac{2}{k^3{\pi }^3}\left(1-\cos \left(k\pi \right)\right)\\ \frac{1}{2}{B}_k=\frac{1}{2}\frac{\Delta p}{\eta l}{h}^2\frac{2}{k^3{\pi }^3}\left(1-\cos \left(k\pi \right)\right),B_k=\{\begin{array}{l}\mathrm{0,}k\text{par}\\ \frac{4}{k^3{\pi }^3}\frac{\Delta p}{\eta l}{h}^2,k\text{impar}\end{array}\end{array}}$

El resultado es

${\displaystyle u_x(y,t)=-\frac{1}{2}\frac{\Delta p}{\eta l}\left(h-y\right)y+\frac{4}{{\pi }^3}\frac{\Delta p}{\eta l}{h}^2{\displaystyle \sum _{k=\mathrm{1,3,5...}}^{\infty }\frac{1}{k^3}\sin \left(k\pi \frac{y}{h}\right)}\exp \left(-\frac{k^2{\pi }^2}{h^2}\upsilon t\right)}$

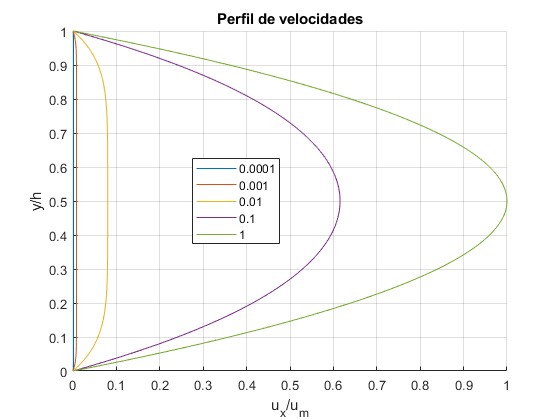
En el estado estacionario, la máxima velocidad del fluido se alcanza en y=h/2

${\displaystyle u_m=-\frac{1}{8}\frac{\Delta p}{\eta l}{h}^2}$

Dividimos u_x(y, t)/u_m

${\displaystyle \frac{u_x(y,t)}{u_m}=4\left(1-\frac{y}{h}\right)\frac{y}{h}-\frac{32}{{\pi }^3}{\displaystyle \sum _{k=\mathrm{1,3,5...}}^{\infty }\frac{1}{k^3}\sin \left(k\pi \frac{y}{h}\right)}\exp \left(-\frac{k^2{\pi }^2}{h^2}\upsilon t\right)}$

Representamos u_x(y,t) en los instantes t=0.0001, 0.001, 0.01, 0.1, 1. Tomamos los 150 primeros términos del desarrollo en serie

yy=linspace(0,1, 200);
ux=zeros(length(yy),1);
hold on
for t=[0.0001,0.001 ,0.01,0.1,1]
    i=0;
    for y=yy
        i=i+1;
        ux(i)=4*(1-y)*y;
        for k=1:2:300
            ux(i)=ux(i)-32*sin(k*pi*y)*exp(-k^2*pi^2*t)/(pi^3*k^3);
        end
    end
    plot(ux,yy,'displayName',num2str(t))
end  
hold off
grid on
legend('-DynamicLegend','location','best')
xlabel('u_x/u_m')
ylabel('y/h')
title('Perfil de velocidades')

Actividades

Se pulsa el botón titulado Nuevo para observar el estado transitorio y su evolución hacia el estado estacionario

Fluido entre dos placas planas y paralelas (III)

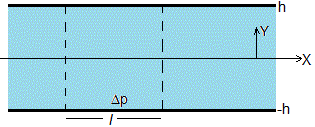
Situamos el fluido entre dos placas planas y paralelas, y=-h e y=h. En el instante t=0, se establece un gradiente de presión a lo largo del eje X, que contiene un término oscilatorio con frecuencia angular ω

${\displaystyle \frac{\partial p}{\partial x}=\frac{p_2-p_1}{x_2-x_1}=\frac{\Delta p}{l}+{\rho }_{f}C\cos \left(\omega t\right)}$

Para determinar el perfil de velocidades u_x(y,t), resolvemos la ecuación diferencial

${\displaystyle {\rho }_f\frac{\partial u_x}{\partial t}=-\frac{\Delta p}{l}-{\rho }_{f}C\cos \left(\omega t\right)+\eta \frac{{\partial }^2{u}_x}{\partial y^2}}$

Con las condiciones de contorno

${\displaystyle \{\begin{array}{l}{u}_x(h,t)=\mathrm{0,}y=h,t>0\\ u_x(-h,t)=\mathrm{0,}y=-h,t>0\end{array}}$

Estado estacionario

Integramos dos veces la ecuación diferencial

${\displaystyle \begin{array}{l}\eta \frac{{\partial }^2{u}_x}{\partial y^2}=\frac{\Delta p}{l}\\ u_x=\frac{1}{2}\frac{\Delta p}{\eta l}{y}^2+c_{1}y+c_2\end{array}}$

Aplicando la condición de contorno, determinamos las constantes c₁ y c₂

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{1}{2}\frac{\Delta p}{\eta l}{h}^2+c_{1}h+c_2=0\\ \frac{1}{2}\frac{\Delta p}{\eta l}{h}^2-c_{1}h+c_2=0\end{array}\\ u_x\left(y,\infty \right)=\frac{1}{2}\frac{\Delta p}{\eta l}\left(y^2-h^2\right)\end{array}}$

El perfil de velocidades es de tipo parabólico en el estado estacionario. La máxima velocidad se alcanza en y=0

${\displaystyle u_m=-\frac{1}{2}\frac{\Delta p}{\eta l}{h}^2}$

La solución de la ecuación diferencial en derivadas parciales u_x(y, t) es la suma del estado estacionario y del estado transitorio

${\displaystyle u_x(y,t)=u_x\left(y,\infty \right)+\Re \left(f(y)\exp \left(i\omega t\right)\right)}$

Donde el símbolo $\Re$, indica la parte real de un número complejo. Introducimos en la ecuación diferencial en derivadas parciales

${\displaystyle \begin{array}{l}{\rho }_f\frac{\partial u_x}{\partial t}=-\frac{\Delta p}{l}-{\rho }_{f}C{e}^{i\omega t}+\eta \frac{{\partial }^2{u}_x}{\partial y^2}\\ {\rho }_f·i\omega ·f(y)e^{i\omega t}=-\frac{\Delta p}{l}-{\rho }_{f}C{e}^{i\omega t}+\eta \left(\frac{\Delta p}{\eta l}+\frac{{\partial }^{2}f}{\partial y^2}{e}^{i\omega t}\right)\\ i\omega ·f(y)=-C+\upsilon \frac{{\partial }^{2}f}{\partial y^2},\upsilon =\frac{\eta }{{\rho }_f}\end{array}}$

Resolvemos la ecuación diferencial

${\displaystyle \frac{d^{2}f}{d{y}^2}-\frac{i\omega }{\upsilon }f=\frac{C}{\upsilon }}$

La solución particular es la constante D

${\displaystyle -\frac{i\omega }{\upsilon }D=\frac{C}{\upsilon },D=\frac{-C}{i\omega }}$

La solución completa es la suma de la homogénea y la particular

${\displaystyle f(y)=A\exp \left(\sqrt{\frac{i\omega }{\upsilon }}y\right)+B\exp \left(-\sqrt{\frac{i\omega }{\upsilon }}y\right)-\frac{C}{i\omega }}$

Teniendo en cuenta la raíz de la unidad imaginaria, obtenemos

${\displaystyle \begin{array}{l}\sqrt{i}=\frac{1+i}{\sqrt{2}}\\ f(y)=A\exp \left((1+i)ky\right)+B\exp \left(-(1+i)ky\right)-\frac{C}{i\omega },k=\sqrt{\frac{\omega }{2\upsilon }}\end{array}}$

Las condiciones de contorno determinan los coeficientes A y B

${\displaystyle \begin{array}{l}\{\begin{array}{l}f(-h)=0\\ f(h)=0\end{array}\\ \{\begin{array}{l}A\exp \left((1+i)kh\right)+B\exp \left(-(1+i)kh\right)-\frac{C}{i\omega }=0\\ A\exp \left(-(1+i)kh\right)+B\exp \left((1+i)kh\right)-\frac{C}{i\omega }=0\end{array}\\ A=B=\frac{C}{i\omega }\frac{1}{\exp \left((1+i)kh\right)+\exp \left(-(1+i)kh\right)}\end{array}}$

La expresión de f(y) es

${\displaystyle \begin{array}{l}f(y)=\frac{C}{i\omega }\frac{\exp \left((1+i)ky\right)+\exp \left(-(1+i)ky\right)}{\exp \left((1+i)kh\right)+\exp \left(-(1+i)kh\right)}-\frac{C}{i\omega }\\ f(y)=\frac{iC}{\omega }\left(1-\frac{e^{ky}\left(\cos \left(ky\right)+i\sin \left(ky\right)\right)+e^{-ky}\left(\cos \left(ky\right)-i\sin \left(ky\right)\right)}{e^{kh}\left(\cos \left(kh\right)+i\sin \left(kh\right)\right)+e^{-kh}\left(\cos \left(kh\right)-i\sin \left(kh\right)\right)}\right)\\ f(y)=\frac{iC}{\omega }\left(1-\frac{\cos \left(ky\right)\left(e^{ky}+e^{-ky}\right)+i\sin \left(ky\right)\left(e^{ky}-e^{-ky}\right)}{\cos \left(kh\right)\left(e^{kh}+e^{-kh}\right)+i\sin \left(kh\right)\left(e^{kh}-e^{-kh}\right)}\right)\\ f(y)=\frac{iC}{\omega }\left(1-\frac{\cos \left(ky\right)\cosh \left(ky\right)+i\sin \left(ky\right)\sinh \left(ky\right)}{\cos \left(kh\right)\cosh \left(kh\right)+i\sin \left(kh\right)\sinh \left(kh\right)}\right)\\ f(y)=\frac{iC}{\omega }\left(1-\frac{\left\{\cos \left(ky\right)\cosh \left(ky\right)+i\sin \left(ky\right)\sinh \left(ky\right)\right\}\left\{\cos \left(kh\right)\cosh \left(kh\right)-i\sin \left(kh\right)\sinh \left(kh\right)\right\}}{\left\{\cos \left(kh\right)\cosh \left(kh\right)+i\sin \left(kh\right)\sinh \left(kh\right)\right\}\left\{\cos \left(kh\right)\cosh \left(kh\right)-i\sin \left(kh\right)\sinh \left(kh\right)\right\}}\right)\\ f(y)=\frac{iC}{\omega }\left(1-\frac{\left\{\cos \left(ky\right)\cosh \left(ky\right)\cos \left(kh\right)\cosh \left(kh\right)+\sin \left(ky\right)\sinh \left(ky\right)\sin \left(kh\right)\sinh \left(kh\right)\right\}+i\left\{\sin \left(ky\right)\sinh \left(ky\right)\cos \left(kh\right)\cosh \left(kh\right)-\cos \left(ky\right)\cosh \left(ky\right)\sin \left(kh\right)\sinh \left(kh\right)\right\}}{{\cos }^2\left(kh\right){\cosh }^2\left(kh\right)+{\sin }^2\left(kh\right){\sinh }^2\left(kh\right)}\right)\\ f(y)=\frac{iC}{\omega }\left(1-\frac{a-ib}{c}\right),\{\begin{array}{l}a=\cos \left(ky\right)\cosh \left(ky\right)\cos \left(kh\right)\cosh \left(kh\right)+\sin \left(ky\right)\sinh \left(ky\right)\sin \left(kh\right)\sinh \left(kh\right)\\ b=\cos \left(ky\right)\cosh \left(ky\right)\sin \left(kh\right)\sinh \left(kh\right)-\sin \left(ky\right)\sinh \left(ky\right)\cos \left(kh\right)\cosh \left(kh\right)\\ c={\cos }^2\left(kh\right){\cosh }^2\left(kh\right)+{\sin }^2\left(kh\right){\sinh }^2\left(kh\right)\end{array}\end{array}}$

La solución de la ecuación diferencial en derivadas parciales u_x(y, t) es

${\displaystyle \begin{array}{l}{u}_x(y,t)=u_x(y,\infty )+\Re \left(\frac{iC}{\omega }\left(1-\frac{a-ib}{c}\right)\exp \left(i\omega t\right)\right)\\ u_x(y,t)=\frac{1}{2}\frac{\Delta p}{\eta l}\left(y^2-h^2\right)+\Re \left(\frac{iC}{\omega }\left(1-\frac{a-ib}{c}\right)\left(\cos \left(\omega t\right)+i\sin \left(\omega t\right)\right)\right)\\ u_x(y,t)=\frac{1}{2}\frac{\Delta p}{\eta l}\left(y^2-h^2\right)-\frac{C}{\omega }\left\{\left(1-\frac{a}{c}\right)\sin \left(\omega t\right)+\frac{b}{c}\cos \left(\omega t\right)\right\}\end{array}}$

Dividiendo por la velocidad máxima $u_m=-\frac{1}{2}\frac{\Delta p}{\eta l}{h}^2$, llegamos a la expresión final del perfil de velocidades del fluido

${\displaystyle \frac{u_x(y,t)}{u_m}=1-\frac{y^2}{h^2}-\frac{C}{\omega u_m}\left\{\left(1-\frac{a}{c}\right)\sin \left(\omega t\right)+\frac{b}{c}\cos \left(\omega t\right)\right\}}$

Nota: En la expresión que figura en la segunda referencia, hay un signo - delante del coeficiente b/c. Como puede comprobar el lector en el código MATLAB, debe tratarse de un error tipográfico

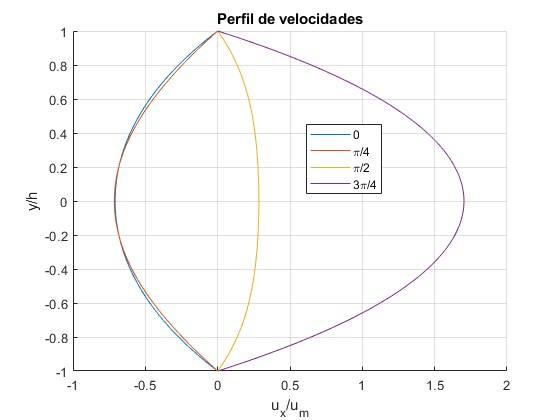
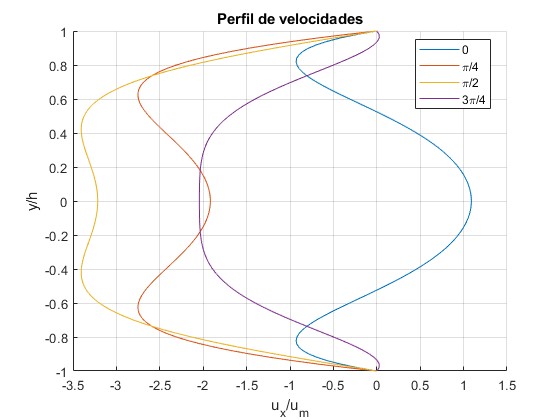
Representamos el perfil de velocidades en los instantes ωt=0, π/4, π/2, 3π/4, para dos valores de $k=\frac{1}{\sqrt{2}},\frac{5}{\sqrt{2}}$, tomando la constante $\frac{C}{\omega u_m}=7$

h=1;
k=1/sqrt(2);
hold on
yy=linspace(-1,1,100);
cte=4;
for wt=[0, pi/4, pi/2, 3*pi/4]
    ux=zeros(1,length(yy));
    j=0;
    for y=yy
        j=j+1;
        a=cos(k*y)*cosh(k*y)*cos(k*h)*cosh(k*h)+sin(k*y)*sinh(k*y)*sin(k*h)*
sinh(k*h);
        b=cos(k*y)*cosh(k*y)*sin(k*h)*sinh(k*h)-sin(k*y)*sinh(k*y)*cos(k*h)*
cosh(k*h);
        c=cos(k*h)^2*cosh(k*h)^2+sin(k*h)^2*sinh(k*h)^2;
        ux(j)=1-y^2/h^2-cte*((1-a/c)*sin(wt)+b*cos(wt)/c);
%       ux(j)=1-y^2/h^2+cte*real((1-cosh((1+1i)*k*y)/cosh((1+1i)*k*h))*
1i*exp(1i*wt));
    end
    plot(ux,yy)
end
hold off
grid on
ylabel('y/h')
legend('0','\pi/4','\pi/2','3\pi/4','location','best')
xlabel('u_x/u_m')
title('Perfil de velocidades')

Actividades

Referencias

Tasos C. Papanastasiou, Georgios C. Georgiou, Andreas N. Alexandrou. Viscous Fluid Flow. CRC Press 2000. Sección 6.6

Michel O. Deville. An Introduction to the Mechanics of Incompressible Fluids. Springer (2022), pp. 68-70