Coordendas cilíndricas

• En forma vectorial

${\displaystyle \begin{array}{l}\nabla ·\overrightarrow{u}=0\\ {\rho }_f\left(\frac{\partial \overrightarrow{u}}{\partial t}+\overrightarrow{u}·\nabla \overrightarrow{u}\right)=-\nabla p+{\rho }_f\overrightarrow{g}+\eta \Delta \overrightarrow{u}\end{array}}$

La primera, es la ecuación de continuidad. p es la presión hidrostática y $\overrightarrow{g}$ la aceleración de la gravedad

• En coordenadas cilíndricas

${\displaystyle \begin{array}{l}\frac{1}{\rho }\frac{\partial \left(\rho u_{\rho }\right)}{\partial \rho }+\frac{1}{\rho }\frac{\partial u_{\phi }}{\partial \phi }+\frac{\partial u_z}{\partial z}=0\\ \{\begin{array}{l}{\rho }_f\left(\frac{\partial u_{\rho }}{\partial t}+u_{\rho }\frac{\partial u_{\rho }}{\partial \rho }+\frac{u_{\phi }}{\rho }\frac{\partial u_{\rho }}{\partial \phi }-\frac{u_{\phi }^2}{\rho }+u_z\frac{\partial u_{\rho }}{\partial z}\right)=-\frac{\partial p}{\partial \rho }+{\rho }_f{g}_{\rho }+\eta \left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_{\rho }}{\partial \rho }\right)-\frac{u_{\rho }}{{\rho }^2}+\frac{1}{{\rho }^2}\frac{{\partial }^2{u}_{\rho }}{\partial {\phi }^2}-\frac{2}{{\rho }^2}\frac{\partial u_{\phi }}{\partial \phi }+\frac{{\partial }^2{u}_{\rho }}{\partial z^2}\right)\\ {\rho }_f\left(\frac{\partial u_{\phi }}{\partial t}+u_{\rho }\frac{\partial u_{\phi }}{\partial \rho }+\frac{u_{\phi }}{\rho }\frac{\partial u_{\phi }}{\partial \phi }+\frac{u_{\rho }{u}_{\phi }}{\rho }+u_z\frac{\partial u_{\phi }}{\partial z}\right)=-\frac{1}{\rho }\frac{\partial p}{\partial \phi }+{\rho }_f{g}_{\phi }+\eta \left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_{\phi }}{\partial \rho }\right)-\frac{u_{\phi }}{{\rho }^2}+\frac{1}{{\rho }^2}\frac{{\partial }^2{u}_{\phi }}{\partial {\phi }^2}+\frac{2}{{\rho }^2}\frac{\partial u_{\rho }}{\partial \phi }+\frac{{\partial }^2{u}_{\phi }}{\partial z^2}\right)\\ {\rho }_f\left(\frac{\partial u_z}{\partial t}+u_{\rho }\frac{\partial u_z}{\partial \rho }+\frac{u_{\phi }}{\rho }\frac{\partial u_z}{\partial \phi }+u_z\frac{\partial u_z}{\partial z}\right)=-\frac{\partial p}{\partial z}+{\rho }_f{g}_z+\eta \left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_z}{\partial \rho }\right)+\frac{1}{{\rho }^2}\frac{{\partial }^2{u}_z}{\partial {\phi }^2}+\frac{{\partial }^2{u}_z}{\partial z^2}\right)\end{array}\end{array}}$

El tensor de esfuerzo viscoso (simétrico)

${\displaystyle \tau =\left(\begin{array}{ccc}{\tau }_{\rho \rho }& {\tau }_{\rho \phi }& {\tau }_{\rho z}\\ {\tau }_{\phi \rho }& {\tau }_{\phi \phi }& {\tau }_{\phi z}\\ {\tau }_{z\rho }& {\tau }_{z\phi }& {\tau }_{zz}\end{array}\right)=\left(\begin{array}{ccc}2\eta \frac{\partial u_{\rho }}{\partial \rho }& \eta \left(\rho \frac{\partial }{\partial \rho }\left(\frac{u_{\phi }}{\rho }\right)+\frac{1}{\rho }\frac{\partial u_{\rho }}{\partial \phi }\right)& \eta \left(\frac{\partial u_{\rho }}{\partial z}+\frac{\partial u_z}{\partial \rho }\right)\\ \eta \left(\rho \frac{\partial }{\partial \rho }\left(\frac{u_{\phi }}{\rho }\right)+\frac{1}{\rho }\frac{\partial u_{\rho }}{\partial \phi }\right)& 2\eta \left(\frac{1}{\rho }\frac{\partial u_{\phi }}{\partial \phi }+\frac{u_{\rho }}{\rho }\right)& \eta \left(\frac{\partial u_{\phi }}{\partial z}+\frac{1}{\rho }\frac{\partial u_z}{\partial \phi }\right)\\ \eta \left(\frac{\partial u_{\rho }}{\partial z}+\frac{\partial u_z}{\partial \rho }\right)& \eta \left(\frac{\partial u_{\phi }}{\partial z}+\frac{1}{\rho }\frac{\partial u_z}{\partial \phi }\right)& 2\eta \frac{\partial u_z}{\partial z}\end{array}\right)}$

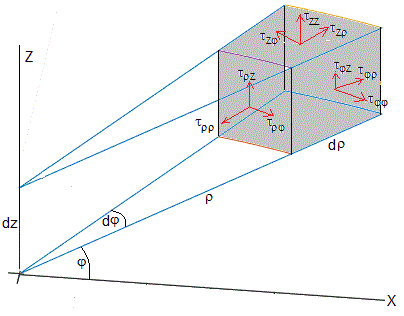
Representamos un elemento de fluido en coordenadas cilíndricas

Flujo en un tubo de sección circular

Sea un tubo de sección circular de radio R, por el que circula un fluido incompresible de densidad ρ_f y viscosidad η

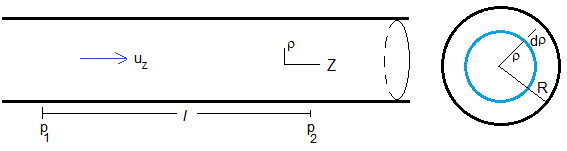
Supondremos

• El tubo es infinitamente largo en la dirección Z
• El flujo es laminar, en el estado estacionario (independiente del tiempo)
• El flujo es paralelo al eje Z, u_ρ=0. u_φ=0 y las derivadas respecto de φ son nulas
• La gravedad no tiene efecto en el movimiento del fluido incompresible

Se aplica un gradiente de presión en la direción Z

${\displaystyle \frac{p_2-p_1}{l}=\frac{\Delta p}{l}}$

El sistema de ecuaciones diferenciales en derivadas parciales en coordenadas cilíndricas se transforma en otro más simple

${\displaystyle \begin{array}{l}\frac{\partial u_z}{\partial z}=0\\ \{\begin{array}{l}0=-\frac{\partial p}{\partial \rho }\\ 0=-\frac{\partial p}{\partial z}+\eta \frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_z}{\partial \rho }\right)\end{array}\end{array}}$

La ecuación de continuidad nos indica que la componente u_z de la velocidad del fluido es función únicamente de ρ

La ecuacion de la presión, nos dice que no depende del radio ρ.

Integramos dos veces la última ecuación diferencial

${\displaystyle \begin{array}{l}\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_z}{\partial \rho }\right)=\frac{\Delta p}{\eta l}\rho \\ \rho \frac{\partial u_z}{\partial \rho }=\frac{1}{2}\frac{\Delta p}{\eta l}{\rho }^2+c_1\\ \frac{\partial u_z}{\partial \rho }=\frac{1}{2}\frac{\Delta p}{\eta l}\rho +\frac{c_1}{\rho }\\ u_z=\frac{1}{4}\frac{\Delta p}{\eta l}{\rho }^2+c_1\ln \rho +c_2\end{array}}$

Las constantes c₁ y c₂ se determinan a partir de las condiciones de contorno: u_z(R)=0. La velocidad del fluido en contacto con las paredes del tubo es nula

La constante c₁ deberá ser nula ya que para ρ=0, tenemos ln(0). Otra razón es que la velocidad es máxima en el eje del tubo, ${\frac{\partial u_z}{\partial \rho }|}_{\rho =0}=0$

Conocida c₁, calculamos la constante c₂

${\displaystyle 0=\frac{1}{4}\frac{\Delta p}{\eta l}{R}^2+c_2}$

El resultado que ya hemos obtenido

${\displaystyle u_z=\frac{1}{4}\frac{\Delta p}{\eta l}{\rho }^2-\frac{1}{4}\frac{\Delta p}{\eta l}{R}^2=\frac{1}{4}\frac{\Delta p}{\eta l}\left({\rho }^2-R^2\right)}$

La velocidad máxima para ρ=0

${\displaystyle u_m=-\frac{1}{4}\frac{\Delta p}{\eta l}{R}^2}$

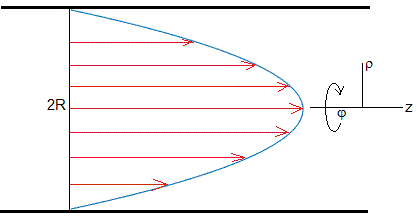
El perfil de velocidades es un paraboloide de revolución al girar la figura alrededor del eje del tubo

El volumen de fluido que atraviesa el área del anillo comprendido entre ρ y ρ+dρ en la unidad de tiempo es u_z(2πρdρ). Donde u_z es la velocidad del fluido a una distancia ρ del eje del tubo y 2πρdρ es el área del anillo

El gasto se calcula integrando

${\displaystyle G={\displaystyle \underset{0}{\overset{R}{\int }}{u}_z\left(2\pi \rho ·d\rho \right)}=\frac{\pi }{2}\frac{\Delta p}{\eta l}{\displaystyle \underset{0}{\overset{R}{\int }}\rho \left({\rho }^2-R^2\right)d\rho }=-\frac{\pi }{8}\frac{\Delta p}{\eta l}{R}^4}$

Tubo hueco

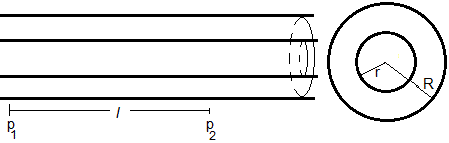
Supongamos ahora un tubo hueco de radio interior r y radio exterior R. Sabiendo que u_z=0, para ρ=r (superficie interior del tubo) y para ρ=R (superficie exterior), calculamos las constantes c₁ y c₂

${\displaystyle \begin{array}{l}0=\frac{1}{4}\frac{\Delta p}{\eta l}{r}^2+c_1\ln r+c_2\\ 0=\frac{1}{4}\frac{\Delta p}{\eta l}{R}^2+c_1\ln R+c_2\end{array}}$

El perfil de velocidades es

${\displaystyle \begin{array}{l}{u}_z=\frac{1}{4}\frac{\Delta p}{\eta l}\left({\rho }^2-\frac{\left(R^2-r^2\right)}{\ln \left(\frac{R}{r}\right)}\ln \rho +\frac{\left(R^2-r^2\right)}{\ln \left(\frac{R}{r}\right)}\ln R-R^2\right)=\frac{1}{4}\frac{\Delta p}{\eta l}{R}^2\left(\frac{{\rho }^2}{R^2}+\frac{\left(1-\frac{r^2}{R^2}\right)}{\ln \left(\frac{R}{r}\right)}\ln \left(\frac{R}{\rho }\right)-1\right)\\ u_z=\frac{1}{4}\frac{\Delta p}{\eta l}\frac{\left({\rho }^2-r^2\right)\ln R-\left(R^2-r^2\right)\ln \rho +\left(R^2-{\rho }^2\right)\ln r}{\ln \left(\frac{R}{r}\right)}\end{array}}$

Perfil de velocidades del tubo hueco

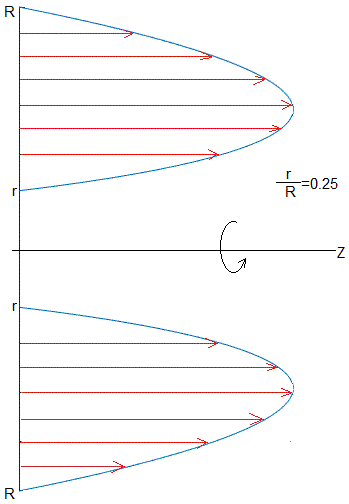
Para representar el perfil de velocidades de ha empleado el código

R=1; %radio exterior
r=0.25; %radio interior
f=@(x) (1-x.^2-(1-(r/R)^2)*log(R./x)/log(R/r));
fplot(f, [r,R])
xlabel('\rho/R')
ylabel('v/v_0')
grid on
title('Perfil de velocidades')
view(90,-90)

La máxima velocidad se obtiene derivando e igualando a cero, du_z/dρ=0

${\displaystyle \begin{array}{l}\frac{d{u}_z}{d\rho }=\frac{1}{4}\frac{\Delta p}{\eta l}\frac{2\rho \ln R-\frac{R^2-r^2}{\rho }-2\rho \ln r}{\ln \left(\frac{R}{r}\right)}=0\\ r_m=\sqrt{\frac{R^2-r^2}{2\ln \left(\frac{R}{r}\right)}}\end{array}}$

>> rm=sqrt((R^2-r^2)/(2*log(R/r)))
rm =    0.5815
>> f(rm)
ans =    0.2952

La máxima velocidad u_z/v₀=0.2952, donde v₀=Δp·R²/(4ηl)

Gasto

Obtenemos el gasto de forma similar a la del tubo, cambiando solamente el límite inferior de la integral, en vez de 0 se pone r radio interior del tubo.

${\displaystyle \begin{array}{l}G={\displaystyle \underset{r}{\overset{R}{\int }}{u}_z\left(2\pi \rho ·d\rho \right)}={\frac{\pi }{2}\frac{\Delta p}{\eta l}\frac{1}{\ln \left(\frac{R}{r}\right)}\left\{\left(\frac{{\rho }^4}{4}-r^2\frac{{\rho }^2}{2}\right)\ln R-\left(R^2-r^2\right)\frac{{\rho }^2}{2}\left(\ln \rho -\frac{1}{2}\right)+\left(R^2\frac{{\rho }^2}{2}-\frac{{\rho }^4}{4}\right)\ln r\right\}|}_r^R=\\ \frac{\pi }{8}\frac{\Delta p}{\eta l}\frac{\left(R^2-r^2\right)\left\{R^2-r^2+\left(R^2+r^2\right)\ln \left(\frac{R}{r}\right)\right\}}{\ln \left(\frac{R}{r}\right)}\end{array}}$

Se ha utilizado el resultado de la integral

${\displaystyle {\displaystyle \int x\ln x·dx=\frac{x^2}{2}}\left(\ln x-\frac{1}{2}\right)}$

Tubo vertical

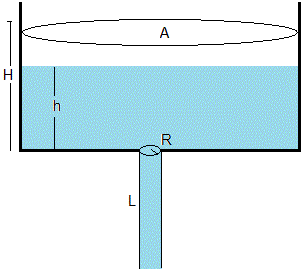
Un depósito cilíndrico de sección A contiene un líquido de densidad ρ_f y visocidad η hasta una altura H. En el fondo del depósito hay un tubo vertical de radio R y longitud L a través del cual se descarga el depósito

En este apartado, vamos a calcular la altura h del líquido en el depósito en en función del tiempo t

Supondremos que el estado transitorio dura un tiempo muy pequeño, el fluido está en cada instante en estado cuasiestacionario

Resolveremos la ecuación de Navier-Stokes en el estado estacionario, teniendo en cuenta que la aceleración de la gravedad g actúa sobre el fluido y la diferencia de presión hidrostática entre el extremo inferior y superior del tubo es ρ_fg(h+L)-ρ_fgL

${\displaystyle \begin{array}{l}0=-\frac{\partial p}{\partial z}-{\rho }_{f}g+\eta \frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_z}{\partial \rho }\right)\\ 0=-\frac{{\rho }_{f}g(h+L)-{\rho }_{f}gL}{L}-{\rho }_{f}g+\eta \frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_z}{\partial \rho }\right)\end{array}}$

Integramos la ecuación diferencial

${\displaystyle \begin{array}{l}\upsilon \frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_z}{\partial \rho }\right)=g\left(\frac{h}{L}+1\right),\upsilon =\frac{\eta }{{\rho }_f}\\ \frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_z}{\partial \rho }\right)=\rho \frac{g}{\upsilon }\left(\frac{h}{L}+1\right)\\ \rho \frac{\partial u_z}{\partial \rho }=\frac{1}{2}\frac{g}{\upsilon }\left(\frac{h}{L}+1\right){\rho }^2+c_1\\ \frac{\partial u_z}{\partial \rho }=\frac{1}{2}\frac{g}{\upsilon }\left(\frac{h}{L}+1\right)\rho +\frac{c_1}{\rho }\\ u_z=\frac{1}{4}\frac{g}{\upsilon }\left(\frac{h}{L}+1\right){\rho }^2+c_1\ln \rho +c_2\end{array}}$

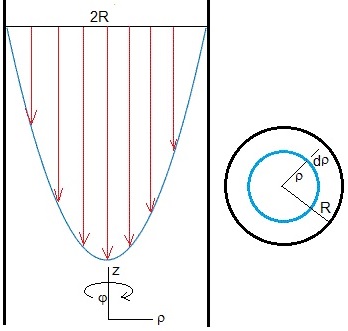
La constante c₁ deberá ser nula ya que para ρ=0, tenemos ln(0).

${\displaystyle u_z=\frac{1}{4}\frac{g}{\upsilon }\left(\frac{h}{L}+1\right){\rho }^2+c_2}$

Las constante c₂ se determina a partir de las condiciones de contorno: u_z(R)=0. La velocidad del fluido en contacto con las paredes del tubo es nula

${\displaystyle \begin{array}{l}{c}_2=-\frac{1}{4}\frac{g}{\upsilon }\left(\frac{h}{L}+1\right)R^2\\ u_z=-\frac{1}{4}\frac{g}{\upsilon }\left(\frac{h}{L}+1\right)\left(R^2-{\rho }^2\right)\end{array}}$

El gasto (volumen por unidad de tiempo) es

${\displaystyle G={\displaystyle \underset{0}{\overset{R}{\int }}\left|u_z\right|\left(2\pi \rho ·d\rho \right)}=\frac{\pi }{2}\frac{g}{\upsilon }\left(\frac{h}{L}+1\right){\displaystyle \underset{0}{\overset{R}{\int }}\rho \left(R^2-{\rho }^2\right)d\rho }=\frac{\pi }{8}\frac{g}{\upsilon }\left(\frac{h}{L}+1\right)R^4}$

La altura h del líquido en el depósito disminuye con el tiempo

${\displaystyle \begin{array}{l}G=-A\frac{dh}{dt}\\ \frac{dh}{dt}=-\left(\frac{\pi R^2}{A}\right)\left(\frac{g{R}^2}{8\upsilon }\right)\left(\frac{h}{L}+1\right)\end{array}}$

Integramos, sabiendo que en el instante t=0, la altura de líquido en el depósito es H

${\displaystyle \begin{array}{l}{\displaystyle \underset{H}{\overset{h}{\int }}\frac{dh}{\frac{h}{L}+1}}=-\frac{\pi R^2}{A}\frac{g{R}^2}{8\upsilon }{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ L\ln \frac{\frac{h}{L}+1}{\frac{H}{L}+1}=-\frac{\pi R^2}{A}\frac{g{R}^2}{8\upsilon }t\\ \frac{h}{L}+1=\left(\frac{H}{L}+1\right)\exp \left(-\frac{\pi R^2}{A}\frac{g{R}^2}{8\upsilon L}t\right)\\ h=\left(H+L\right)\exp \left(-\frac{\pi R^2}{A}\frac{g{R}^2}{8\upsilon L}t\right)-L\end{array}}$

Se vacía el depósito, en el instante t_f tal que h=0

${\displaystyle \begin{array}{l}L=\left(H+L\right)\exp \left(-\frac{\pi R^2}{A}\frac{g{R}^2}{8\upsilon L}{t}_f\right)\\ t_f=\frac{A}{\pi R^2}\frac{8\upsilon L}{g{R}^2}\ln \left(\frac{H}{L}+1\right)\end{array}}$

Ejemplo

• Radio del tubo, R=0.0026
• Longitud del tubo vertical, L=0.14 m
• Sección del depósito, A=0.0057 m²
• Altura inicial de líquido en el depósito, H=0.09 m
• Viscosidad cinemática de la glicerina, ν=η/ρ=773.8·10^-6 m²/s

R=0.0026; %radio del tubo vertical
L=0.14; %longitud del tubo
A=0.0057; %sección del depósito
H=0.09; %altura del líquido en el depósito
nu=773.8e-6; %visosidad cinemática de la glicerina
k=pi*R^4*9.8/(8*A*nu*L);
f=@(t) (H+L)*exp(-k*t)-L;
tf=log(H/L+1)/k;
fplot(f,[0,tf])
grid on
xlabel('t')
ylabel('h')
title('Altura del depósito')

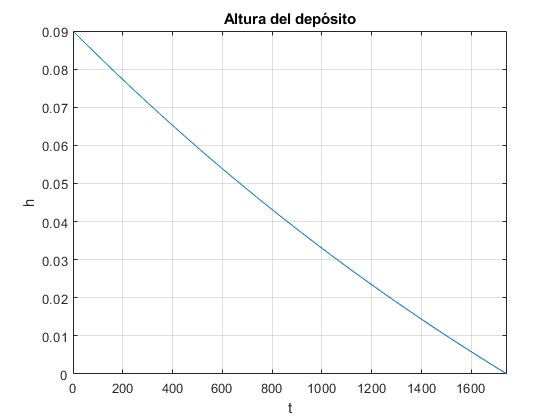
Fluido entre dos cilindros coaxiales muy largos

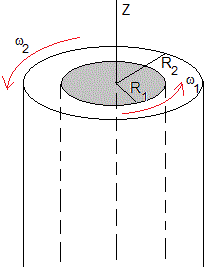
Consideremos dos cilindros coaxiales de radios R₁ el macizo y R₂ el hueco. Giran con velocidad angular constante ω₁ y ω₂, respectivamente, alrededor del eje común Z.

La componente de la velocidad del fluido u_z y sus derivadas son nulas. La velocidad del fluido incompresible no depende de z, por lo que se reduce el sistema de ecuaciones diferenciales en derivadas parciales

Por otra parte, el problema tiene simetría alrededor del eje de rotación Z, por lo que las componentes u_ρ y u_φ de la velocidad del fluido y sus derivadas no dependen de φ

En el estado estacionario, el sistema de ecuaciones diferenciales en derivadas parciales se reduce a

${\displaystyle \begin{array}{l}\frac{1}{\rho }\frac{\partial \left(\rho u_{\rho }\right)}{\partial \rho }=0\\ \{\begin{array}{l}{\rho }_f\left(u_{\rho }\frac{\partial u_{\rho }}{\partial \rho }-\frac{u_{\phi }^2}{\rho }\right)=-\frac{\partial p}{\partial \rho }+\eta \left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_{\rho }}{\partial \rho }\right)-\frac{u_{\rho }}{{\rho }^2}\right)\\ {\rho }_f\left(u_{\rho }\frac{\partial u_{\phi }}{\partial \rho }+\frac{u_{\rho }{u}_{\phi }}{\rho }\right)=\eta \left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_{\phi }}{\partial \rho }\right)-\frac{u_{\phi }}{{\rho }^2}\right)\end{array}\end{array}}$

La componente u_ρ es nula en las paredes del recipiente R₁ y R₂, donde las componentes de la velocidad del fluido son u_φ(R₁)=ω₁R₁ y u_φ(R₂)=ω₂R₂

La solución de la ecuación de continuidad es

${\displaystyle \begin{array}{l}{u}_{\rho }=\frac{c}{\rho }\\ u_{\rho }\left(R_1\right)=\frac{c}{R_1}=0\\ u_{\rho }\left(R_2\right)=\frac{c}{R_2}=0\\ c=\mathrm{0,}{u}_{\rho }=0\end{array}}$

El sistema de ecuaciones diferenciales en derivadas parciales se reduce aún más

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\rho }_f\left(-\frac{u_{\phi }^2}{\rho }\right)=-\frac{\partial p}{\partial \rho }\\ 0=\eta \left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_{\phi }}{\partial \rho }\right)-\frac{u_{\phi }}{{\rho }^2}\right)\end{array}\\ \{\begin{array}{l}\frac{\partial p}{\partial \rho }={\rho }_f\frac{u_{\phi }^2}{\rho }\\ \frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_{\phi }}{\partial \rho }\right)-\frac{u_{\phi }}{\rho }=0\end{array}\end{array}}$

Para la segunda ecuación diferencial, buscamos una solución en forma de serie infinita

${\displaystyle u_{\phi }={\displaystyle \sum _{n=-\infty }^{n=\infty }{a}_n{\rho }^n}}$

Introduciendo en la ecuación diferencial

${\displaystyle \begin{array}{l}{u}_{\phi }={\displaystyle \sum _{n=-\infty }^{n=\infty }{a}_n{\rho }^n}\\ \frac{\partial }{\partial \rho }\left({\displaystyle \sum _{n=-\infty }^{n=\infty }{a}_{n}n{\rho }^n}\right)={\displaystyle \sum _{n=-\infty }^{n=\infty }{a}_n{\rho }^{n-1}}\\ {\displaystyle \sum _{n=-\infty }^{n=\infty }{a}_n{n}^2{\rho }^{n-1}}={\displaystyle \sum _{n=-\infty }^{n=\infty }{a}_n{\rho }^{n-1}}\\ n^2=1\end{array}}$

La solución consta de dos términos, como puede comprobarse por simple sustitución en la ecuación diferencial

${\displaystyle u_{\phi }=A\rho +\frac{B}{\rho }}$

Determinamos los coeficientes A y B a partir de las condiciones de contorno: u_φ(R₁)=ω₁R₁ y u_φ(R₂)=ω₂R₂

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\omega }_1{R}_1=A{R}_1+\frac{B}{R_1}\\ {\omega }_2{R}_2=A{R}_2+\frac{B}{R_2}\end{array}\\ A=\frac{{\omega }_2{R}_2^2-{\omega }_1{R}_1^2}{R_2^2-R_1^2},B=\frac{{\omega }_1-{\omega }_2}{R_2^2-R_1^2}{R}_2^2{R}_1^2\\ u_{\phi }=\frac{1}{R_2^2-R_1^2}\left\{\left({\omega }_2{R}_2^2-{\omega }_1{R}_1^2\right)\rho -\left({\omega }_2-{\omega }_1\right)R_2^2{R}_1^2\frac{1}{\rho }\right\}\end{array}}$

Representamos la componente u_φ de la velocidad del fluido entre los dos cilindros, para R₁/R₂=0.5 y para dos valores de ω₁/ω₂=4 y 0.2

${\displaystyle u_{\phi }=\frac{R_2{\omega }_2}{1-\frac{R_1^2}{R_2^2}}\left\{\left(1-\frac{{\omega }_1}{{\omega }_2}\frac{R_1^2}{R_2^2}\right)\frac{\rho }{R_2}-\left(1-\frac{{\omega }_1}{{\omega }_2}\right)\frac{R_1^2}{R_2^2}\frac{1}{\frac{\rho }{R_2}}\right\}}$

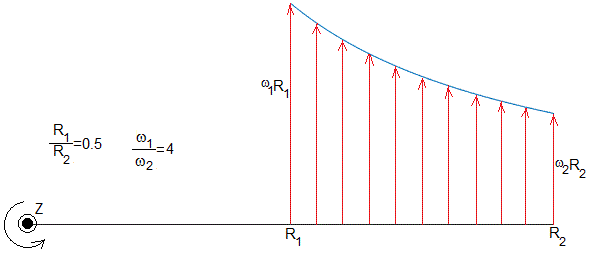
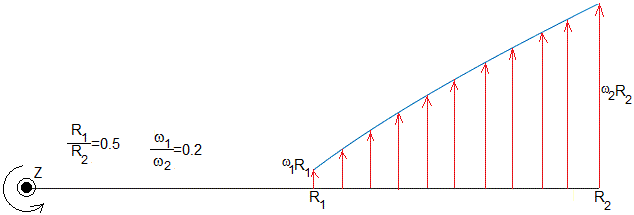
Casos particulares:

• Un solo cilindro, R₂→∞

Cuando tenemos un cilindro de radio R₁ girando con velocidad angular ω₁ en un fluido de extensión infinita. El perfil de velocidades es

${\displaystyle u_{\phi }={\omega }_1\frac{R_1^2}{\rho }}$



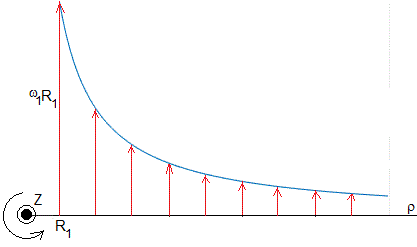
La componente u_φ de la velocidad disminuye inversamente proporcional a la distancia ρ al eje de rotación.

• Fluido contenido en un cilindro de radio R₂, R₁=0

${\displaystyle u_{\phi }={\omega }_2\rho }$



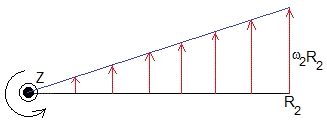
La componente u_φ de la velocidad es proporcional a la distancia ρ al eje de rotación.

Presión

Determinamos la presión p resolviendo la primera ecuación diferencial

${\displaystyle \begin{array}{l}\frac{\partial p}{\partial \rho }={\rho }_f\frac{1}{\rho }{\left(A\rho +\frac{B}{\rho }\right)}^2={\rho }_f\left(A^2\rho +\frac{B^2}{{\rho }^3}+2\frac{AB}{\rho }\right)\\ \frac{p-p(R_1)}{{\rho }_f}={\displaystyle \underset{R_1}{\overset{\rho }{\int }}\left(A^2\rho +\frac{B^2}{{\rho }^3}+2\frac{AB}{\rho }\right)d\rho }={\frac{1}{2}{A}^2{\rho }^2-\frac{1}{2}\frac{B^2}{{\rho }^2}+2AB\ln \rho |}_{R_1}^{\rho }=\\ \frac{1}{2}{A}^2\left({\rho }^2-R_1^2\right)-\frac{B^2}{2}\left(\frac{1}{{\rho }^2}-\frac{1}{R_1^2}\right)+2AB\ln \frac{\rho }{R_1}\end{array}}$

El resultado es

${\displaystyle \frac{p}{{\rho }_f}=\frac{p(R_1)}{{\rho }_f}+\frac{1}{{\left(R_2^2-R_1^2\right)}^2}\left\{{\left({\omega }_2{R}_2^2-{\omega }_1{R}_1^2\right)}^2\frac{{\rho }^2-R_1^2}{2}-{\left({\omega }_1-{\omega }_2\right)}^2\frac{R_2^4{R}_1^4}{2}\left(\frac{1}{{\rho }^2}-\frac{1}{R_1^2}\right)+2\left({\omega }_2{R}_2^2-{\omega }_1{R}_1^2\right)\left({\omega }_1-{\omega }_2\right)R_2^2{R}_1^2\ln \frac{\rho }{R_1}\right\}}$

Esfuerzo viscoso

${\displaystyle \begin{array}{l}{\tau }_{\rho \phi }=\eta \left(\rho \frac{\partial }{\partial \rho }\left(\frac{u_{\phi }}{\rho }\right)+\frac{1}{\rho }\frac{\partial u_{\rho }}{\partial \phi }\right)\\ {\tau }_{\rho \phi }=\eta \rho \frac{\partial }{\partial \rho }\left(\frac{u_{\phi }}{\rho }\right)=-2\eta \rho \frac{B}{{\rho }^3}=-2\eta \frac{B}{{\rho }^2}\end{array}}$

Ya que u_ρ=0 y su derivada, por simetría alrededor del eje Z, no depende de φ. La fuerza en la longitud l del cilindro es

${\displaystyle \frac{F}{2\pi R_1·l}=-2\eta \frac{B}{R_1^2}}$

El momento de esta fuerza respecto del eje de rotación es

${\displaystyle M=F·R_1=4\pi \eta l\frac{{\omega }_2-{\omega }_1}{R_2^2-R_1^2}{R}_2^2{R}_1^2}$

Resultado que ya hemos obtenido en la página titulada Fluido entre dos cilindros coaxiales de una forma más sencilla

Dos fluidos inmiscibles

Consideremos dos fluidos inmiscibles (agua y aceite) de densidades ρ₁ y ρ₂ y viscosidades η₁ y η₂, respectivamente. El primer fluido es una capa cilíndica de radios R₁ y r del eje del cilindro y el segundo, una capa cilíndrica de radios r y R₂, tal como se aprecia en la figura.

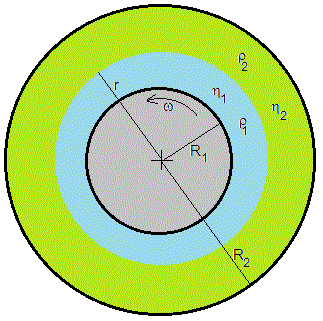
El cilindro interior de radio R₁ gira con velocidad angular constante ω. El cilidro hueco de radio R₂ permence en reposo

Para calcular las velocidades u_1φ y u_2φ de los dos fluidos, resolveremos las ecuaciones diferenciales

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_{1\phi }}{\partial \rho }\right)-\frac{u_{1\phi }}{\rho }=0\\ \frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_{2\phi }}{\partial \rho }\right)-\frac{u_{2\phi }}{\rho }=0\end{array}\\ \{\begin{array}{l}{u}_{1\phi }=A_1\rho +\frac{B_1}{\rho }\\ u_{2\phi }=A_2\rho +\frac{B_2}{\rho }\end{array}\end{array}}$

Las condiciones de contorno, determinan los cuatro coeficientes A₁, A₂, B₁, B₂

${\displaystyle \begin{array}{l}{u}_{1\phi }(R_1)=\omega R_1\\ u_{2\phi }(R_2)=0\end{array}}$

En la superficie de separación ρ=r, las velocidades de los dos fluidos coinciden

${\displaystyle \begin{array}{l}{u}_{1\phi }(r)=u_{2\phi }(r)\\ A_{1}r+\frac{B_1}{r}=A_{2}r+\frac{B_2}{r}\end{array}}$

El esfuero viscoso τ_ρφ de un fluido sobre el otro coinciden

${\displaystyle \begin{array}{l}{\tau }_{\rho \phi }=-2\eta \frac{B}{{\rho }^2}\\ -2{\eta }_1\frac{B_1}{r^2}=-2{\eta }_2\frac{B_2}{r^2}\end{array}}$

Resolvemos el sistema de cuatro ecuaciones con cuatro incógnitas

${\displaystyle \begin{array}{l}\{\begin{array}{l}{A}_1{R}_1+\frac{B_1}{R_1}=\omega R_1\\ A_2{R}_2+\frac{B_2}{R_2}=0\\ A_{1}r+\frac{B_1}{r}=A_{2}r+\frac{B_2}{r}\\ {\eta }_1{B}_1={\eta }_2{B}_2\end{array}\\ A_1=\omega \frac{\frac{{\eta }_1}{{\eta }_2}\left(\frac{R_1^2}{r^2}-\frac{R_1^2}{R_2^2}\right)-\frac{R_1^2}{r^2}}{k},k=1-\frac{R_1^2}{r^2}+\frac{{\eta }_1}{{\eta }_2}\left(\frac{R_1^2}{r^2}-\frac{R_1^2}{R_2^2}\right)\\ B_1=\omega \frac{R_1^2}{k},B_2=\omega \frac{{\eta }_1}{{\eta }_2}\frac{R_1^2}{k},A_2=-\frac{\omega }{k}\frac{{\eta }_1}{{\eta }_2}\frac{R_1^2}{R_2^2}\end{array}}$

Representamos el perfil de velocidades

${\displaystyle \{\begin{array}{l}{u}_{1\phi }=A_1\rho +\frac{B_1}{\rho }\\ u_{2\phi }=A_2\rho +\frac{B_2}{\rho }\end{array}}$

para R₁=1, R₂=2, r=1.5, para dos valores del cociente η₁/η₂=0.5, 2

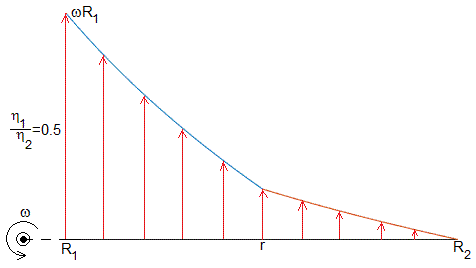
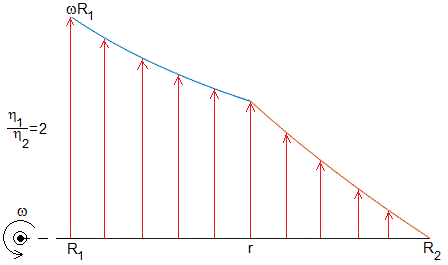
eta=0.5; %eta_1/eta_2
R1=1; %radios
R2=2;
r=1.5; 
k=1-R1^2/r^2+eta*(R1^2/r^2-R1^2/R2^2);
A1=(eta*(R1^2/r^2-R1^2/R2^2)-R1^2/r^2)/k;
B1=R1^2/k;
A2=-eta*R1^2/(k*R2^2);
B2=eta*R1^2/k;
hold on
u1=@(y) A1*y+B1./y;
u2=@(y) A2*y+B2./y;
fplot(u1,[R1,r])
fplot(u2,[r,R2])
hold off
xlabel('\rho')
ylabel('u_\phi/\omega')
title('Perfil de velocidades')

Fluido entre dos cilindros coaxiales porosos

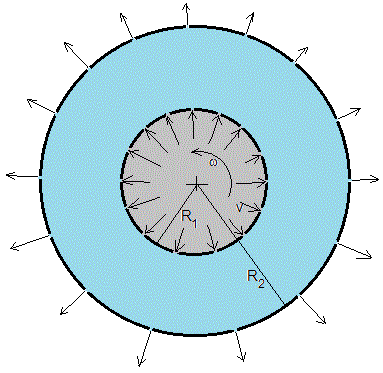
Consideremos dos cilindros coaxiales de radios R₁ el macizo y R₂ el hueco. El primero gira con velocidad angular constante ω, alrededor del eje común Z. El cilindro hueco permenece en reposo

Ambos cilindros son porosos y el fluido que entra por el cilindro macizo con velocidad v y sale por el cilindro hueco, tal como se muestra en la figura. Vamos a determinar el perfil u_φ(ρ) de la velocidad del fluido en el espacio comprendido entre los dos cilindros, R₁<ρ<R₂

Como en el aparado anterior, el flujo no depende de z, se elimina la tercera ecuación diferencial en derivadas parciales

El flujo tiene simetría de revolución alrededor del eje Z, no depende de φ ni de sus derivadas.

En este caso, la componente u_ρ≠0

El sistema de ecuaciones diferenciales en derivadas parciales se reduce a

${\displaystyle \begin{array}{l}\frac{1}{\rho }\frac{\partial \left(\rho u_{\rho }\right)}{\partial \rho }=0\\ \{\begin{array}{l}{\rho }_f\left(u_{\rho }\frac{\partial u_{\rho }}{\partial \rho }-\frac{u_{\phi }^2}{\rho }\right)=-\frac{\partial p}{\partial \rho }+\eta \left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_{\rho }}{\partial \rho }\right)-\frac{u_{\rho }}{{\rho }^2}\right)\\ {\rho }_f\left(u_{\rho }\frac{\partial u_{\phi }}{\partial \rho }+\frac{u_{\rho }{u}_{\phi }}{\rho }\right)=\eta \left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_{\phi }}{\partial \rho }\right)-\frac{u_{\phi }}{{\rho }^2}\right)\end{array}\end{array}}$

Las condiciones de contorno son:

• u_ρ=v para ρ=R₁

• u_φ=ωR₁ para ρ=R₁, u_φ=0, para ρ=R₂

La ecuación de continuidad nos indica que ρu_φ=cte. En la superficie del ciclindro macizo, ρ=R₁

${\displaystyle \begin{array}{l}{R}_{1}v=\rho u_{\rho }\\ u_{\rho }=\frac{R_{1}v}{\rho }\end{array}}$

La última ecuación diferencial se transforma en

${\displaystyle \begin{array}{l}\frac{v{R}_1}{\rho }\frac{\partial u_{\phi }}{\partial \rho }+v{R}_1\frac{u_{\phi }}{{\rho }^2}=\upsilon \left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_{\phi }}{\partial \rho }\right)-\frac{u_{\phi }}{{\rho }^2}\right),\upsilon =\frac{\eta }{{\rho }_f}\\ \frac{\partial \left(\rho u_{\phi }\right)}{\partial \rho }=\frac{\upsilon }{v{R}_1}{\rho }^2\frac{\partial }{\partial \rho }\left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho u_{\phi }\right)\right)\end{array}}$

Llamamos z=ρu_φ

${\displaystyle \begin{array}{l}\frac{\partial z}{\partial \rho }=\frac{1}{k}{\rho }^2\frac{\partial }{\partial \rho }\left(\frac{1}{\rho }\frac{\partial z}{\partial \rho }\right),z=\rho u_{\phi },k=\frac{v{R}_1}{\upsilon }=\frac{v{R}_1{\rho }_f}{\eta }\\ \frac{1}{\rho }\frac{\partial z}{\partial \rho }=\frac{1}{k}\rho \frac{\partial }{\partial \rho }\left(\frac{1}{\rho }\frac{\partial z}{\partial \rho }\right)\end{array}}$

Llamamos s a la derivada de z/ρ

${\displaystyle \begin{array}{l}s=\frac{1}{k}\rho \frac{\partial s}{\partial \rho },s=\frac{1}{\rho }\frac{\partial z}{\partial \rho }\\ \frac{\partial s}{s}=k\frac{\partial \rho }{\rho }\\ \ln s=k\ln \rho +\ln c_1\\ s=c_1{\rho }^k\end{array}}$

Deshaciendo los cambios de variable

${\displaystyle \begin{array}{l}{c}_1{\rho }^k=\frac{1}{\rho }\frac{\partial z}{\partial \rho }\\ z=\frac{c_1{\rho }^{k+2}}{k+2}+c_2\\ u_{\phi }=\frac{z}{\rho }=\frac{c_1{\rho }^{k+1}}{k+2}+\frac{c_2}{\rho }\end{array}}$

Los coeficientes c₁ y c₂ se determinan a partir de la condiciones de contorno

${\displaystyle \begin{array}{l}\{\begin{array}{l}\omega R_1=\frac{c_1{R}_1^{k+1}}{k+2}+\frac{c_2}{R_1}\\ 0=\frac{c_1{R}_2^{k+1}}{k+2}+\frac{c_2}{R_2}\end{array}\\ c_1=-\frac{\omega R_1^2\left(k+2\right)}{R_2^{k+2}-R_1^{k+2}},c_2=\frac{\omega R_1^2}{R_2^{k+2}-R_1^{k+2}}{R}_2^{k+2}\\ u_{\phi }=\omega R_1^2\frac{\left(R_2^{k+2}-{\rho }^{k+2}\right)}{\rho \left(R_2^{k+2}-R_1^{k+2}\right)}\end{array}}$

En forma adimensional

${\displaystyle \frac{u_{\phi }}{\omega R_1}=\frac{\left(R^{k+2}-x^{k+2}\right)}{x\left(R^{k+2}-1\right)},x=\frac{\rho }{R_1},R=\frac{R_2}{R_1}}$

Caso particular, k=-2

Este caso hay que resolverlo separadamente

${\displaystyle \begin{array}{l}{c}_1{\rho }^{-2}=\frac{1}{\rho }\frac{\partial z}{\partial \rho }\\ \frac{\partial z}{\partial \rho }=\frac{c_1}{\rho }\\ z=c_1\ln \rho +c_2\\ u_{\phi }=\frac{z}{\rho }=\frac{1}{\rho }\left(c_1\ln \rho +c_2\right)\end{array}}$

Los coeficientes c₁ y c₂ se determinan a partir de la condiciones de contorno

${\displaystyle \begin{array}{l}\{\begin{array}{l}\omega R_1=\frac{1}{R_1}\left(c_1\ln R_1+c_2\right)\\ 0=\frac{1}{R_2}\left(c_1\ln R_2+c_2\right)\end{array}\\ u_{\phi }=\omega R_1^2\frac{\ln \left(\frac{R_2}{\rho }\right)}{\rho \ln \left(\frac{R_2}{R_1}\right)}\end{array}}$

En forma adimensional

${\displaystyle \frac{u_{\phi }}{\omega R_1}=\frac{\ln \left(\frac{R}{x}\right)}{x\ln \left(R\right)},x=\frac{\rho }{R_1},R=\frac{R_2}{R_1}}$

R=2; %R2/R1
hold on
k=-2;
f=@(x) log(R./x)./(x*log(R));
fplot(f,[1,2],'displayName',num2str(k))
for k=[0,2,4]
    f=@(x) (R^(k+2)-x.^(k+2))./(x*(R^(k+2)-1));
    fplot(f,[1,2],'displayName',num2str(k))
end  
hold off
grid on
legend('-DynamicLegend','location','best')
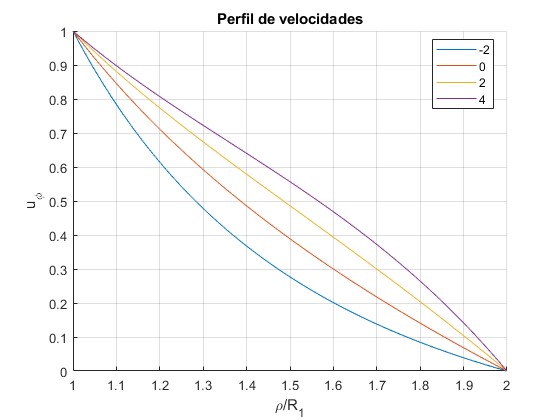
xlabel('\rho/R_1')
ylabel('u_\phi')
title('Perfil de velocidades')

Referencias

C. Neipp, A. Hernández, T. Beléndez, J.J. Rodes, A. Beléndez. Three approaches to calculating the velocity profile of a laminar incompressible fluid in a hollow tube. Am. J. Phys. 71 (1) January 2003, pp. 46-48

Michel O. Deville. An Introduction to the Mechanics of Incompressible Fluids. Springer (2022), pp. 58-62

Charles R. (Chuck) Smith. Introduction to Graduate Fluid Mechanics. Fourth Edition. Self-Published, 2023. pp. 164-177

Don S. Lemons, Trevor C. Lipsombe, Rickey J. Faehl. Vertical quasistatic Poiseuille flow: Theory and experiment. Am. J. Phys. 90 (1), January 2022. pp. 59-63