Fluido en un tubo de sección circular (I)

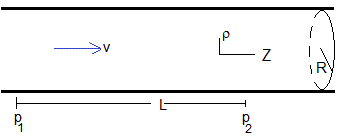
Se sitúa un fluido en un tubo horizontal de sección circular, de radio R. En el instante t=0, se establece un gradiente de presión a lo largo del eje Z

${\displaystyle \frac{\partial p}{\partial x}=\frac{p_2-p_1}{x_2-x_1}=\frac{\Delta p}{l}}$

En este apartado, vamos a resolver la ecuación diferencial en derivadas parciales

${\displaystyle {\rho }_f\frac{\partial u_z}{\partial t}=-\frac{\Delta p}{l}+\eta \frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_z}{\partial \rho }\right)}$

Con la condición de contorno e inicial siguientes:

${\displaystyle \begin{array}{l}{u}_z(R,t)=\mathrm{0,}\rho =R,t\ge 0\\ u_z(\rho \mathrm{,0})=\mathrm{0,}0\le \rho \le R,t=0\end{array}}$

El fluido parte del reposo en el instante t=0

Ya hemos estudiado la solución de la ecuación diferencial independiente del tiempo, t, el estado estacionario

${\displaystyle u_z\left(\rho ,\infty \right)=-\frac{1}{4}\frac{\Delta p}{\eta l}\left(R^2-{\rho }^2\right)}$

El perfil de velocidades en el instante t, u_x(ρ,t) es la suma del perfil en el estado estacionario y en el estado transitorio

${\displaystyle u_z(\rho ,t)=-\frac{1}{4}\frac{\Delta p}{\eta l}\left(R^2-{\rho }^2\right)-u_z^t(\rho ,t)}$

Introducimos esta expresión en la ecuación diferencial, para obtener la correspondiente al estado transitorio

${\displaystyle \frac{\partial u_z^t}{\partial t}=\upsilon \frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_z^t}{\partial \rho }\right)}$

Resolvemos esta ecuación diferencial en derivadas paraciales con las condiciones de contorno e inicial, siguientes

${\displaystyle \begin{array}{l}{u}_z^t(R,t)=\mathrm{0,}\rho =R,t\ge 0\\ u_z^t(\rho \mathrm{,0})=\frac{1}{4}\frac{\Delta p}{\eta l}\left(R^2-{\rho }^2\right),0\le \rho \le R,t=0\end{array}}$

Variables separadas

Expresamos la solución de la ecuación diferencial como producto de dos funciones una que depende de la variable ρ y otra que depende de la variable t

${\displaystyle \begin{array}{l}{u}_z^t(\rho ,t)=X(\rho )T(t)\\ \frac{1}{T}\frac{dT}{dt}=\upsilon \frac{1}{X}\frac{1}{\rho }\frac{d}{d\rho }\left(\rho \frac{dX}{d\rho }\right)\end{array}}$

El miembro izquierdo, solamente depende de t y el derecho solamente de ρ. Transformamos una ecuación diferencial en derivadas parciales en un sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{1}{\upsilon T}\frac{dT}{dt}=-\frac{{\alpha }^2}{R^2}\\ \frac{1}{X}\frac{1}{\rho }\frac{d}{d\rho }\left(\rho \frac{dX}{d\rho }\right)=-\frac{{\alpha }^2}{R^2}\end{array}\\ \{\begin{array}{l}\frac{dT}{dt}+\frac{{\alpha }^2\upsilon }{h^2}T=0\\ \frac{d^{2}X}{d{\rho }^2}+\frac{1}{\rho }\frac{dX}{d\rho }+\frac{{\alpha }^2}{R^2}X=0\end{array}\end{array}}$

La solución de la primera ecuación diferencial es

${\displaystyle T(t)=c_0\exp \left(-\frac{{\alpha }^2\upsilon }{R^2}t\right)}$

En la segunda hacemos primero, el cambio de variable r=αρ/R. Su solución se expresa en términos de funciones de Bessel

${\displaystyle \begin{array}{l}\frac{d^{2}X}{d{r}^2}+\frac{1}{r}\frac{dX}{dr}+X=0\\ r^2\frac{d^{2}X}{d{r}^2}+r\frac{dX}{dr}+r^{2}X=0\\ X=c_1{J}_0(r)+c_2{Y}_0(r)\\ X=c_1{J}_0\left(\frac{\alpha }{R}\rho \right)+c_2{Y}_0\left(\frac{\alpha }{R}\rho \right)\end{array}}$

Dado que Y₀(x)→∞ cuando x→0, el coeficiente c₂=0

${\displaystyle X(\rho )=c_1{J}_0\left(\frac{\alpha }{R}\rho \right)}$

Aplicamos la condición de contorno en ρ=R

${\displaystyle \begin{array}{l}{u}_z^t(R,t)=X(R)T(t)=\mathrm{0,}X(R)=0\\ J_0\left(\alpha \right)=\mathrm{0,}{\alpha }_k,k=\mathrm{1,2,3...}\end{array}}$

α_k son las raíces de la ecuación transcendente, J₀(x)=0

La solución de la ecuación diferencial en derivadas parciales, es la superposición

${\displaystyle u_z^t(\rho ,t)={\displaystyle \sum _{k=1}^{\infty }{B}_k{J}_0\left({\alpha }_k\frac{\rho }{R}\right)}\exp \left(-\frac{{\alpha }_k^2}{R^2}\upsilon t\right)}$

Los coeficientes B_k se determinan a partir de la condición inicial

${\displaystyle \begin{array}{l}{u}_z^t(\rho \mathrm{,0})=\frac{1}{4}\frac{\Delta p}{\eta l}\left(R^2-{\rho }^2\right)\\ \frac{1}{4}\frac{\Delta p}{\eta l}\left(R^2-{\rho }^2\right)={\displaystyle \sum _{k=1}^{\infty }{B}_k{J}_0\left({\alpha }_k\frac{\rho }{R}\right)}\end{array}}$

Teniendo en cuenta la relación de ortogonalidad

${\displaystyle {\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0(k_{m}x)J_0(k_{n}x)dx}=\{\begin{array}{l}\mathrm{0,}m\ne n\\ \frac{1}{2}{J}_1^2(k_m),m=n\end{array}}$

Resolvemos las integrales, haciendo el cambio de variable z=ρ/R.

${\displaystyle \begin{array}{l}{\displaystyle \sum _{k=1}^{\infty }{B}_k{\displaystyle \underset{0}{\overset{R}{\int }}{J}_0\left({\alpha }_k\frac{\rho }{R}\right)J_0\left({\alpha }_n\frac{\rho }{R}\right)}\rho ·d\rho =-{\displaystyle \underset{0}{\overset{R}{\int }}\frac{1}{4}\frac{\Delta p}{\eta l}\left({\rho }^2-R^2\right)J_0\left({\alpha }_n\frac{\rho }{R}\right)\rho ·d\rho }}\\ B_k{\displaystyle \underset{0}{\overset{1}{\int }}{J}_0^2\left({\alpha }_{k}z\right)}z·dz=-\frac{1}{4}\frac{\Delta p}{\eta l}{R}^2{\displaystyle \underset{0}{\overset{1}{\int }}\left(z^2-1\right)J_0\left({\alpha }_{k}z\right)z·dz}\\ B_k\frac{1}{2}{J}_1^2\left({\alpha }_k\right)=-\frac{1}{4}\frac{\Delta p}{\eta l}{R}^2{\displaystyle \underset{0}{\overset{1}{\int }}\left(z^2-1\right)J_0\left({\alpha }_{k}z\right)z·dz}\\ B_k\frac{1}{2}{J}_1^2\left({\alpha }_k\right)=-\frac{1}{4}\frac{\Delta p}{\eta l}{R}^2\left(\frac{4}{{\alpha }_k^3}{J}_1\left({\alpha }_k\right)-\frac{2}{{\alpha }_k^2}{J}_0\left({\alpha }_k\right)\right)\\ B_k=-2\frac{\Delta p}{\eta l}{R}^2\frac{1}{{\alpha }_k^3{J}_1\left({\alpha }_k\right)}\end{array}}$

>> syms x k;
>> int((1-x^2)*besselj(0,k*x)*x,0,1)
 ans =(4*besselj(1, k))/k^3 - (2*besselj(0, k))/k^2

El estado transitorio es

${\displaystyle u_z^t(\rho ,t)=-2\frac{\Delta p}{\eta l}{R}^2{\displaystyle \sum _{k=1}^{\infty }\frac{1}{{\alpha }_k^3{J}_1\left({\alpha }_k\right)}{J}_0\left({\alpha }_k\frac{\rho }{R}\right)}\exp \left(-\frac{{\alpha }_k^2}{R^2}\upsilon t\right)}$

El resultado final es la suma del estado estacionario y el estado transitorio

${\displaystyle u_z(\rho ,t)=-\frac{1}{4}\frac{\Delta p}{\eta l}\left(R^2-{\rho }^2\right)+2\frac{\Delta p}{\eta l}{R}^2{\displaystyle \sum _{k=1}^{\infty }\frac{1}{{\alpha }_k^3{J}_1\left({\alpha }_k\right)}{J}_0\left({\alpha }_k\frac{\rho }{R}\right)}\exp \left(-\frac{{\alpha }_k^2}{R^2}\upsilon t\right)}$

La velocidad máxima en el estado estacionario, se alcanza para ρ=0, en el eje Z

${\displaystyle u_m=-\frac{1}{4}\frac{\Delta p}{\eta l}{R}^2}$

Dividimos entre u_m para que todas las magnitudes sean adimensionales

${\displaystyle \frac{u_z(\rho ,t)}{u_m}=\left(1-\frac{{\rho }^2}{R^2}\right)-8{\displaystyle \sum _{k=1}^{\infty }\frac{1}{{\alpha }_k^3{J}_1\left({\alpha }_k\right)}{J}_0\left({\alpha }_k\frac{\rho }{R}\right)}\exp \left(-\frac{{\alpha }_k^2}{R^2}\upsilon t\right)}$

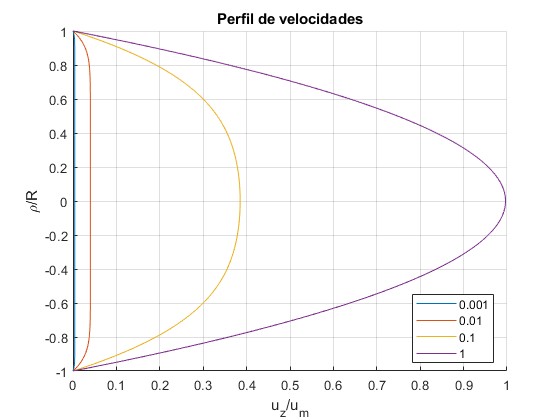
Representamos u_z(ρ,t)/u_m en los instantes t=0.001, 0.01, 0.1, 1. Tomamos los 12 raíces α_k de la ecuación transcendente J₀(x)=0

function navier_stokes_12
    x=linspace(0,40,40);
    f=@(x) besselj(0,x);
    alfa=raices(f,x); 
  
    rr=linspace(-1,1, 400);
    uz=zeros(length(rr),1);
    hold on
    for t=[0.001 ,0.01,0.1,1]
        i=0;
        for r=rr
            i=i+1;
            uz(i)=1-r^2;
            for j=1:length(alfa)
                uz(i)=uz(i)-8*besselj(0, alfa(j)*r)*exp(-alfa(j)^2*t)
/(alfa(j)^3*besselj(1,alfa(j)));
            end
        end
        plot(uz,rr,'displayName',num2str(t))
    end  
    hold off
    grid on
    legend('-DynamicLegend','location','best')
    xlabel('u_z/u_m')
    ylabel('\rho/R')
    title('Perfil de velocidades')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end

end

Actividades

Se pulsa el botón titulado Nuevo para observar el estado transitorio y su evolución hacia el estado estacionario

Fluido en un tubo de sección circular (II)

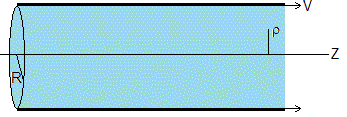
Se sitúa un fluido en un tubo horizontal de sección circular, de radio R. En el instante t=0, se desplaza el tubo con velocidad constante V a lo largo del eje Z

En este apartado, vamos a resolver la ecuación diferencial en derivadas parciales

${\displaystyle \begin{array}{l}{\rho }_f\frac{\partial u_z}{\partial t}=\eta \frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_z}{\partial \rho }\right)\\ \frac{\partial u_z}{\partial t}=\upsilon \left(\frac{{\partial }^2{u}_z}{\partial {\rho }^2}+\frac{1}{\rho }\frac{\partial u_z}{\partial \rho }\right)\end{array}}$

Con la condición de contorno e inicial

${\displaystyle \begin{array}{l}{u}_z(R,t)=V,\rho =R,t\ge 0\\ u_z(\rho \mathrm{,0})=\mathrm{0,}t=0\end{array}}$

El fluido parte del reposo en el instante t=0

Hacemos los cambios de variable, obteniendo una ecuación diferencial en derivadas parciales con magnitudes adimensionales

${\displaystyle \begin{array}{l}u=\frac{V-u_z}{V},x=\frac{\rho }{R},\tau =\frac{\upsilon t}{R^2}\\ \frac{\partial u}{\partial \tau }=\frac{{\partial }^{2}u}{\partial x^2}+\frac{1}{x}\frac{\partial u}{\partial x}\end{array}}$

La condición de contorno e inicial son ahora

${\displaystyle \begin{array}{l}u(\mathrm{1,}\tau )=\mathrm{0,}x=\mathrm{1,}\tau \ge 0\\ u(x\mathrm{,0})=\mathrm{1,}\tau =0\end{array}}$

Variables separadas

Expresamos la solución de la ecuación diferencial como producto de dos funciones una que depende de la variable x y otra que depende de la variable τ

${\displaystyle \begin{array}{l}u(x,\tau )=F(x)T(\tau )\\ F\frac{dT}{d\tau }=T\left(\frac{d^{2}F}{d{x}^2}+\frac{1}{x}\frac{dF}{dx}\right)\\ \frac{1}{T}\frac{dT}{d\tau }=\frac{1}{F}\left(\frac{d^{2}F}{d{x}^2}+\frac{1}{x}\frac{dF}{dx}\right)\end{array}}$

El miembro izquierdo, solamente depende de τ y el derecho solamente de x. Transformamos una ecuación diferencial en derivadas parciales en un sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{1}{T}\frac{dT}{d\tau }=-{\lambda }^2\\ \frac{1}{F}\left(\frac{d^{2}F}{d{x}^2}+\frac{1}{x}\frac{dF}{dx}\right)=-{\lambda }^2\end{array}\\ \{\begin{array}{l}\frac{dT}{d\tau }+{\lambda }^{2}T=0\\ \frac{d^{2}F}{d{x}^2}+\frac{1}{x}\frac{dF}{dx}+{\lambda }^{2}F=0\end{array}\end{array}}$

La solución de la primera ecuación diferencial es

${\displaystyle T=C\exp \left(-{\lambda }^2\tau \right)}$

En la segunda, hacemos primero, el cambio de variable y=λx. Su solución se expresa en términos de funciones de Bessel

${\displaystyle \begin{array}{l}{x}^2\frac{d^{2}F}{d{x}^2}+x\frac{dF}{dx}+{\lambda }^2{x}^{2}F=0\\ y^2\frac{d^{2}F}{d{y}^2}+y\frac{dF}{dy}+y^{2}F=\mathrm{0,}y=\lambda x\\ F(y)=A{J}_0(y)+B{Y}_0(y)\end{array}}$

Dado que Y₀(x)→∞ cuando x→0, el coeficiente B=0. La solución es

${\displaystyle u(x,\tau )=A{J}_0(\lambda x)\exp \left(-{\lambda }^2\tau \right)}$

Aplicamos la condición de contorno en x=1, u(1, τ)=0

${\displaystyle \begin{array}{l}u(\mathrm{1,}\tau )=A{J}_0(\lambda )\exp \left(-{\lambda }^2\tau \right)=0\\ J_0(\lambda )=0\end{array}}$

λ_n son las raíces de la ecuación transcendente, J₀(x)=0

La solución de la ecuación diferencial en derivadas parciales, es la superposición

${\displaystyle u(x,\tau )={\displaystyle \sum _{n=1}^{\infty }{A}_n}{J}_0({\lambda }_{n}x)\exp \left(-{\lambda }_n^2\tau \right)}$

Los coeficientes A_n se determinan a partir de la condición inicial

${\displaystyle \begin{array}{l}u(x\mathrm{,0})={\displaystyle \sum _{n=1}^{\infty }{A}_n}{J}_0({\lambda }_{n}x)\\ 1={\displaystyle \sum _{n=1}^{\infty }{A}_n}{J}_0({\lambda }_{n}x)\end{array}}$

Teniendo en cuenta la relación de ortogonalidad

${\displaystyle {\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0(k_{m}x)J_0(k_{n}x)dx}=\{\begin{array}{l}\mathrm{0,}m\ne n\\ \frac{1}{2}{J}_1^2(k_m),m=n\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}x·J_0({\lambda }_{m}x)dx}={\displaystyle \sum _{n=1}^{\infty }{A}_n{\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0({\lambda }_{n}x)J_0({\lambda }_{m}x)dx}}\\ {\displaystyle \underset{0}{\overset{1}{\int }}x·J_0({\lambda }_{n}x)dx}=A_n{\displaystyle \underset{0}{\overset{1}{\int }}x{J}_0^2({\lambda }_{n}x)dx}\\ A_n=\frac{{\displaystyle \underset{0}{\overset{1}{\int }}x·J_0({\lambda }_{n}x)dx}}{\frac{1}{2}{J}_1^2\left({\lambda }_n\right)}\end{array}}$

Simplificamos esta expresión, teniendo en cuenta la propiedad

${\displaystyle {\displaystyle \underset{0}{\overset{1}{\int }}{x}^{n+1}{J}_n(ax)dx}=\frac{1}{a}{J}_{n+1}(a)}$

Obtenemos, finalmente

${\displaystyle A_n=\frac{\frac{1}{{\lambda }_n}{J}_1\left({\lambda }_n\right)}{\frac{1}{2}{J}_1^2\left({\lambda }_n\right)}=\frac{2}{{\lambda }_n{J}_1\left({\lambda }_n\right)}}$

La solución u(x, τ) se expresa

${\displaystyle u(x,\tau )=2{\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\lambda }_n}\frac{J_0({\lambda }_{n}x)}{J_1\left({\lambda }_n\right)}}\exp \left(-{\lambda }_n^2\tau \right)}$

Deshaciendo el cambio de variable

${\displaystyle \begin{array}{l}u=\frac{V-u_z}{V},x=\frac{\rho }{R},\tau =\frac{\upsilon t}{R^2}\\ \frac{V-u_z(\rho ,t)}{V}=2{\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\lambda }_n}\frac{J_0\left({\lambda }_n\frac{\rho }{R}\right)}{J_1\left({\lambda }_n\right)}}\exp \left(-{\lambda }_n^2\frac{\upsilon t}{R^2}\right)\\ u_z(\rho ,t)=V\left(1-2{\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\lambda }_n}\frac{J_0\left({\lambda }_n\frac{\rho }{R}\right)}{J_1\left({\lambda }_n\right)}}\exp \left(-{\lambda }_n^2\frac{\upsilon t}{R^2}\right)\right)\end{array}}$

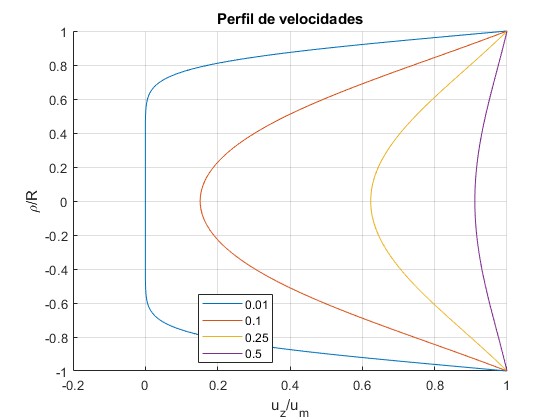
Representamos el perfil de velocidades u_z(ρ,τ)/V, en función de ρ/R, para los instantes τ= 0.01, 0.1, 0.25, 0.5

function navier_stokes_21
    x=linspace(0,40,40);
    f=@(x) besselj(0,x);
    lambda=raices(f,x); 

    rr=linspace(-1,1, 400);
    uz=zeros(length(rr),1);
    hold on
    for tau=[0.01 ,0.1, 0.25, 0.5]
        i=0;
        for r=rr
            i=i+1;
            uz(i)=1;
            for j=1:length(lambda)
                uz(i)=uz(i)-2*besselj(0,lambda(j)*r)*exp(-lambda(j)^2*tau)
/(lambda(j)*besselj(1,lambda(j)));
            end
        end
        plot(uz,rr,'displayName',num2str(tau))
    end  
    hold off
    grid on
    legend('-DynamicLegend','location','best')
    xlabel('u_z/u_m')
    ylabel('\rho/R')
    title('Perfil de velocidades')

   function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

Actividades

Se pulsa el botón titulado Nuevo para observar la evolución del perfil de velocidades del fluido en un tubo que se mueve con velocidad constante

Fluido en un tubo de sección circular (III)

Se sitúa un fluido en un tubo horizontal de sección circular, de radio R. En el instante t=0, se establece un gradiente de presión oscilante lo largo del eje Z

${\displaystyle \frac{\partial p}{\partial z}={\rho }_f{c}_n\cos \left(n\omega t\right),n=\mathrm{1,2,3...}}$

En este apartado, vamos a resolver la ecuación diferencial en derivadas parciales

${\displaystyle \begin{array}{l}{\rho }_f\frac{\partial u_z}{\partial t}=-\frac{\partial p}{\partial z}+\eta \frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_z}{\partial \rho }\right)\\ {\rho }_f\frac{\partial u_z}{\partial t}=-{\rho }_f{c}_n\cos \left(n\omega t\right)+\eta \left(\frac{{\partial }^2{u}_z}{\partial {\rho }^2}+\frac{1}{\rho }\frac{\partial u_z}{\partial \rho }\right)\end{array}}$

Con las condiciones de contorno

${\displaystyle u_z(R,t)=\mathrm{0,}\rho =R,t\ge 0}$

Buscamos una solución de la forma

${\displaystyle u_z\left(\rho ,t\right)=\Re \left(f\left(\rho \right)\exp \left(i\omega nt\right)\right)}$

Donde el símbolo $\Re$, indica la parte real de un número complejo. Introducimos en la ecuación diferencial en derivadas parciales

${\displaystyle \begin{array}{l}in\omega {\rho }_f\Re \left(\exp \left(i\omega nt\right)\right)f\left(\rho \right)=-{\rho }_f{c}_n\cos \left(n\omega t\right)+\eta \left(\frac{d^{2}f}{d{\rho }^2}+\frac{1}{\rho }\frac{df}{d\rho }\right)\Re \left(\exp \left(i\omega nt\right)\right)\\ \frac{d^{2}f}{d{\rho }^2}+\frac{1}{\rho }\frac{df}{d\rho }-\frac{in\omega }{\upsilon }f=\frac{c_n}{\upsilon },\upsilon =\frac{\eta }{{\rho }_f}\end{array}}$

• Solución particular

La solución particular de esta ecuación diferencial es una constante C. Introduciendo en la ecuación diferencial

${\displaystyle \begin{array}{l}-\frac{in\omega }{\upsilon }C=\frac{c_n}{\upsilon }\\ C=-\frac{c_n}{in\omega }\end{array}}$

• Solución de la ecuación diferencial homogénea

Hacemos el cambio z=ρ/R, para expresar la solución en términos de una variable adimensional

${\displaystyle \frac{d^{2}f}{d{z}^2}+\frac{1}{z}\frac{df}{dz}-R^2\frac{in\omega }{\upsilon }f=0}$

Hacemos otro cambio de variable para obtener una ecuación diferencial cuya solución se expresa en términos de las funciones de Bessel J₀(x) y Y₀(x)

${\displaystyle \begin{array}{l}x=iR\sqrt{\frac{in\omega }{\upsilon }}z\\ \frac{i^2{R}^{2}in\omega }{\upsilon }\left(\frac{d^{2}f}{d{x}^2}+\frac{1}{x}\frac{df}{dx}\right)-R^2\frac{in\omega }{\upsilon }f=0\\ x^2\frac{d^{2}f}{d{x}^2}+x\frac{df}{dx}+x^{2}f=0\\ f_h(x)=A{J}_0(x)+B{Y}_0(x)\end{array}}$

Dado que Y₀(x)→∞ cuando x→0, el coeficiente B=0

${\displaystyle f_h(\rho )=A{J}_0\left(iR\sqrt{\frac{in\omega }{\upsilon }}z\right)=A{J}_0\left(\alpha \sqrt{n}z{i}^{3/2}\right),\alpha =R\sqrt{\frac{\omega }{\upsilon }}=R\sqrt{\frac{{\rho }_f\omega }{\eta }}}$

Teniendo en cuenta que la viscosidad en S.I. se mide en kg/(m·s), α es un número adimensional denominado de Womersley, si este número es grande los efectos de la viscosidad se reducen a una región próxima a las paredes del tubo de radio R

La solución completa es la suma de ambas

${\displaystyle f(\rho )=A{J}_0\left(\alpha \sqrt{n}\frac{\rho }{R}{i}^{3/2}\right)-\frac{c_n}{in\omega }}$

El coeficiente A se determina a partir de la condición de contorno

${\displaystyle \begin{array}{l}f(R)=0\\ A=\frac{c_n}{in\omega J_0\left(\alpha \sqrt{n}{i}^{3/2}\right)}\end{array}}$

La solución de la ecuación diferencial en derivadas parciales es

${\displaystyle u_z\left(\rho ,t\right)=\Re \left(\frac{i{c}_n}{n\omega }\left(1-\frac{J_0\left(\alpha \sqrt{n}\frac{\rho }{R}{i}^{3/2}\right)}{J_0\left(\alpha \sqrt{n}{i}^{3/2}\right)}\right)\exp \left(i\omega nt\right)\right)}$

Teniendo en cuenta la definición de α, número de Womersley

${\displaystyle \begin{array}{l}\omega n=\frac{{\alpha }^{2}n}{R^2}\upsilon \\ u_z\left(\rho ,t\right)=\frac{R^2}{\upsilon }{\displaystyle \sum _{n=1}^{\infty }\Re \left(\frac{i{c}_n}{{\alpha }^{2}n}\left(1-\frac{J_0\left(\alpha \sqrt{n}\frac{\rho }{R}{i}^{3/2}\right)}{J_0\left(\alpha \sqrt{n}{i}^{3/2}\right)}\right)\exp \left(i\omega nt\right)\right)}\end{array}}$

Representamos el perfil de velocidades para n=1, c₁=2/π, dos valores del número α=3.34 y 5.78 en los instantes tales que ωt=0, π/6, π/3, π/2, 2π/3, 5π/6, π (0, 30, 60, 90, 120, 150, 180)

hold on
n=1;
alfa=3.34; %nú.mero de Womersley
c1=2/pi; %coeficiente
for wt=(0:30:180)*pi/180
    f=@(x) real(1i*c1*(1-besselj(0, alfa*sqrt(n)*x*1i^(3/2))/
besselj(0,alfa*sqrt(n)*1i^(3/2)))*exp(1i*n*wt)/(alfa^2*n));
    fplot(f,[-1,1])
end
hold off
xlabel('\rho/R'); 
legend('0','\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6','\pi','location','best')
ylabel('u_z(\rho,t)')
grid on
hold off
title('Perfil de velocidades')

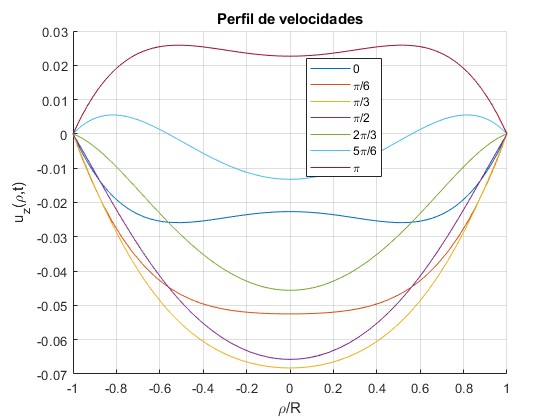
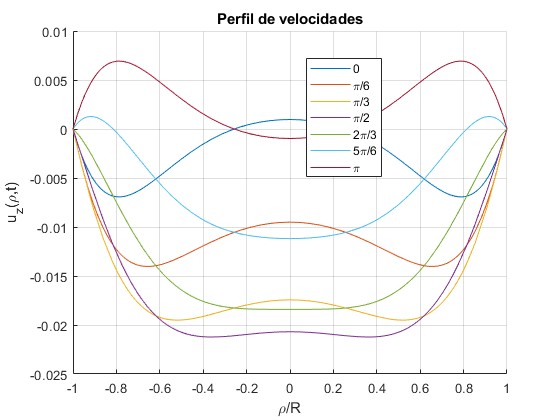
Cambiamos α=5.78

Superposión

Consideremos un gradiente de presión que es una función periódica del tiempo de forma cualesquiera, de periodo P o frecuencia angular ω=2π/P

${\displaystyle \frac{\partial p}{\partial z}=c_0+{\displaystyle \sum _{n=1}^{\infty }{c}_n\exp \left(in\omega t\right)}}$

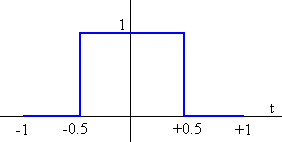
Por ejemplo, en la página titulada Series de Fourier, estudiamos la función periódica, pulso rectangular de periodo P=2, frecuencia angular, ω=π

${\displaystyle \frac{\partial p}{\partial z}={\rho }_f\left(\frac{1}{2}+\frac{2}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5..}}^{\infty }{\left(-1\right)}^{(n-1)/2}\frac{\cos \left(n\pi t\right)}{n}}\right)}$

Los coeficientes de la serie son c₀=1/2, c₁=2/π, c₃=-2/(3π), c₅=2/(5π), ...

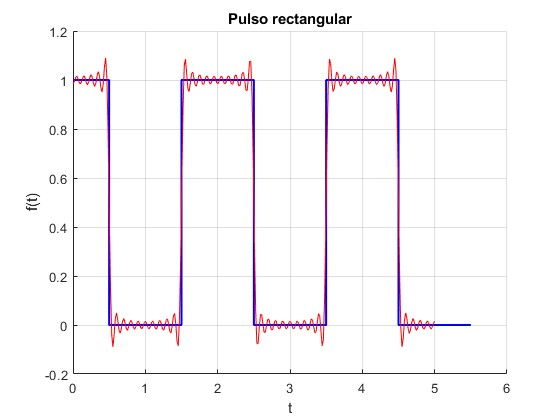
Representamos aproximadamente, los pulsos rectangulares mediante la suma de 10 términos del desarrollo en serie

n=20;
hold on
x=[0,0.5,0.5,1.5,1.5,2.5,2.5,3.5,3.5,4.5,4.5, 5.5];
y=[1,1,0,0,1,1,0,0,1,1,0,0];
plot(x,y,'b','linewidth',1.5)
x=linspace(0,5,300);
y=zeros(length(x),1);
for i=1:length(x)
    y(i)=1/2;
    for k=1:2:n
        y(i)=y(i)+(-1)^((k-1)/2)*2*cos(k*pi*x(i))/(k*pi);
     end
end
plot(x,y, 'r');
title('Pulso rectangular')
xlabel('t'); 
ylabel('f(t)')
grid on
hold off

En el estado estacionario, bajo un gradiente de presión

${\displaystyle \begin{array}{l}\frac{\Delta p}{l}={\rho }_f{c}_0\\ u_z(\rho ,\infty )=-\frac{1}{4}\frac{\Delta p}{\eta l}\left(R^2-{\rho }^2\right)=-\frac{1}{4}\frac{c_0}{\upsilon }{R}^2\left(1-\frac{{\rho }^2}{R^2}\right)\end{array}}$

Para un gradiente de presión representado por una función periódica cuyos coeficientes c_n, n=0,1,2,3,.. son conocidos, el perfil de velocidades es la superposición

${\displaystyle u_z\left(\rho ,t\right)=-\frac{1}{4}\frac{c_0}{\upsilon }{R}^2\left(1-\frac{{\rho }^2}{R^2}\right)+\frac{R^2}{\upsilon }{\displaystyle \sum _{n=1}^{\infty }\Re \left(\frac{i{c}_n}{{\alpha }^{2}n}\left(1-\frac{J_0\left(\alpha \sqrt{n}\frac{\rho }{R}{i}^{3/2}\right)}{J_0\left(\alpha \sqrt{n}{i}^{3/2}\right)}\right)\exp \left(i\omega nt\right)\right)}}$

Fluido en un cilindro de altura infinita

Se sitúa un fluido en un cilindro vertical, de radio R y altura muy grande. En el instante t=0, se le proporciona una velocidad angular de rotación ω

En este apartado, vamos a resolver la ecuación diferencial en derivadas parciales

${\displaystyle {\rho }_f\frac{\partial u_{\phi }}{\partial t}=\eta \left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_{\phi }}{\partial \rho }\right)-\frac{u_{\phi }}{{\rho }^2}\right)}$

Con las condiciones de contorno e inicial siguientes:

${\displaystyle \begin{array}{l}{u}_{\phi }(R,t)=\omega R,\rho =R,t\ge 0\\ u_z(\rho \mathrm{,0})=\mathrm{0,}0\le \rho \le R,t=0\end{array}}$

El fluido parte del reposo en el instante t=0

Ya hemos estudiado la solución de la ecuación diferencial independiente del tiempo, t, el estado estacionario

${\displaystyle u_{\phi }\left(\rho ,\infty \right)=\omega \rho }$

El perfil de velocidades en el instante t, u_x(ρ,t) es la suma del perfil en el estado estacionario y en el estado transitorio

${\displaystyle u_{\phi }(\rho ,t)=\omega \rho -u_{\phi }^t(\rho ,t)}$

Introducimos esta expresión en la ecuación diferencial, para obtener la correspondiente al estado transitorio

${\displaystyle \frac{\partial u_{\phi }^t}{\partial t}=\upsilon \left(\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial u_{\phi }^t}{\partial \rho }\right)-\frac{u_{\phi }^t}{{\rho }^2}\right),\upsilon =\frac{\eta }{{\rho }_f}}$

Resolvemos esta ecuación diferencial en derivadas paraciales con las condiciones de contorno e inicial, siguientes

${\displaystyle \begin{array}{l}{u}_{\phi }^t(R,t)=\mathrm{0,}\rho =R,t\ge 0\\ u_{\phi }^t(\rho \mathrm{,0})=\omega \rho ,0\le \rho \le R,t=0\end{array}}$

Variables separadas

Expresamos la solución de la ecuación diferencial como producto de dos funciones una que depende de la variable ρ y otra que depende de la variable t

${\displaystyle \begin{array}{l}{u}_z^t(\rho ,t)=X(\rho )T(t)\\ X\frac{dT}{dt}=\upsilon T\left(\frac{1}{\rho }\frac{dX}{d\rho }+\frac{d^{2}X}{d{\rho }^2}-\frac{X}{{\rho }^2}\right)\end{array}}$

El miembro izquierdo, solamente depende de t y el derecho solamente de ρ. Transformamos una ecuación diferencial en derivadas parciales en un sistema de dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{1}{\upsilon T}\frac{dT}{dt}=-\frac{{\alpha }^2}{R^2}\\ \frac{1}{X}\left(\frac{1}{\rho }\frac{dX}{d\rho }+\frac{d^{2}X}{d{\rho }^2}-\frac{X}{{\rho }^2}\right)=-\frac{{\alpha }^2}{R^2}\end{array}\\ \{\begin{array}{l}\frac{dT}{dt}+\frac{{\alpha }^2\upsilon }{h^2}T=0\\ \frac{d^{2}X}{d{\rho }^2}+\frac{1}{\rho }\frac{dX}{d\rho }+\left(\frac{{\alpha }^2}{R^2}-\frac{1}{{\rho }^2}\right)X=0\end{array}\end{array}}$

La solución de la primera ecuación diferencial es

${\displaystyle T(t)=c_0\exp \left(-\frac{{\alpha }^2\upsilon }{R^2}t\right)}$

En la segunda hacemos primero, el cambio de variable r=αρ/R. Su solución se expresa en términos de funciones de Bessel

${\displaystyle \begin{array}{l}\frac{d^{2}X}{d{r}^2}+\frac{1}{r}\frac{dX}{dr}+\left(1-\frac{1}{r^2}\right)X=0\\ r^2\frac{d^{2}X}{d{r}^2}+r\frac{dX}{dr}+\left(r^2-1\right)X=0\\ X=c_1{J}_1(r)+c_2{Y}_1(r)\\ X=c_1{J}_1\left(\frac{\alpha }{R}\rho \right)+c_2{Y}_1\left(\frac{\alpha }{R}\rho \right)\end{array}}$

Dado que Y₁(x)→∞ cuando x→0, el coeficiente c₂=0

${\displaystyle X(\rho )=c_1{J}_1\left(\frac{\alpha }{R}\rho \right)}$

Aplicamos la condición de contorno en ρ=R

${\displaystyle \begin{array}{l}{u}_x^t(R,t)=X(R)T(t)=\mathrm{0,}X(R)=0\\ J_1\left(\alpha \right)=\mathrm{0,}{\alpha }_k,k=\mathrm{1,2,3...}\end{array}}$

α_k son las raíces de la ecuación transcendente, J₁(x)=0

La solución de la ecuación diferencial en derivadas parciales, es la superposición

${\displaystyle u_x^t(\rho ,t)={\displaystyle \sum _{k=1}^{\infty }{B}_k{J}_1\left({\alpha }_k\frac{\rho }{R}\right)}\exp \left(-\frac{{\alpha }_k^2}{R^2}\upsilon t\right)}$

Los coeficientes B_k se determinan a partir de la condición inicial

${\displaystyle \begin{array}{l}{u}_x^t(\rho \mathrm{,0})=\omega \rho \\ \omega \rho ={\displaystyle \sum _{k=1}^{\infty }{B}_k{J}_1\left({\alpha }_k\frac{\rho }{R}\right)}\end{array}}$

Teniendo en cuenta la relación de ortogonalidad

${\displaystyle {\displaystyle \underset{0}{\overset{1}{\int }}x{J}_1(k_{m}x)J_1(k_{n}x)dx}=\{\begin{array}{l}\mathrm{0,}m\ne n\\ \frac{1}{2}{J}_2^2(k_m),m=n\end{array}}$

Resolvemos las integrales, haciendo el cambio de variable z=ρ/R.

${\displaystyle \begin{array}{l}{\displaystyle \sum _{k=1}^{\infty }{B}_k{\displaystyle \underset{0}{\overset{R}{\int }}{J}_1\left({\alpha }_k\frac{\rho }{R}\right)J_1\left({\alpha }_n\frac{\rho }{R}\right)}\rho ·d\rho ={\displaystyle \underset{0}{\overset{R}{\int }}\omega \rho J_1\left({\alpha }_n\frac{\rho }{R}\right)\rho ·d\rho }}\\ B_k{\displaystyle \underset{0}{\overset{1}{\int }}z{J}_1^2\left({\alpha }_{k}z\right)}dz=\omega R{\displaystyle \underset{0}{\overset{1}{\int }}{z}^2{J}_1\left({\alpha }_{k}z\right)dz}\\ B_k\frac{1}{2}{J}_2^2\left({\alpha }_k\right)=\omega R\frac{1}{{\alpha }_k}{J}_2\left({\alpha }_k\right)\\ B_k=\frac{2\omega R}{{\alpha }_k{J}_2\left({\alpha }_k\right)}\end{array}}$

El estado transitorio es

${\displaystyle u_{\phi }^t(\rho ,t)=2\omega R{\displaystyle \sum _{k=1}^{\infty }\frac{1}{{\alpha }_k{J}_2\left({\alpha }_k\right)}{J}_1\left({\alpha }_k\frac{\rho }{R}\right)}\exp \left(-\frac{{\alpha }_k^2}{R^2}\upsilon t\right)}$

El resultado final es la suma del estado estacionario y el estado transitorio

${\displaystyle u_{\phi }(\rho ,t)=\omega \rho -2\omega R{\displaystyle \sum _{k=1}^{\infty }\frac{1}{{\alpha }_k{J}_2\left({\alpha }_k\right)}{J}_1\left({\alpha }_k\frac{\rho }{R}\right)}\exp \left(-\frac{{\alpha }_k^2}{R^2}\upsilon t\right)}$

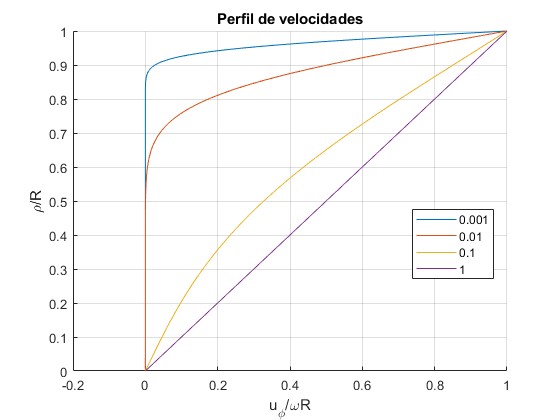
Dividimos entre ωR para que todas las magnitudes sean adimensionales

${\displaystyle \frac{u_{\phi }(\rho ,t)}{\omega R}=\frac{\rho }{R}-2{\displaystyle \sum _{k=1}^{\infty }\frac{1}{{\alpha }_k{J}_2\left({\alpha }_k\right)}{J}_1\left({\alpha }_k\frac{\rho }{R}\right)}\exp \left(-\frac{{\alpha }_k^2}{R^2}\upsilon t\right)}$

Representamos u_z(ρ,t)/ωR en los instantes t=0.001, 0.01, 0.1, 1. Tomamos los 12 raíces α_k de la ecuación transcendente J₀(x)=0

function navier_stokes_13
    x=linspace(0,80,80);
    f=@(x) besselj(1,x);
    alfa=raices(f,x); 
     disp(alfa)

    rr=linspace(0,1, 200);
    uz=zeros(length(rr),1);
    hold on
    for t=[0.001 ,0.01,0.1,1]
        i=0;
        for r=rr
            i=i+1;
            uz(i)=r;
            for j=1:length(alfa)
                uz(i)=uz(i)-2*besselj(1, alfa(j)*r)*exp(-alfa(j)^2*t)/
(alfa(j)*besselj(2,alfa(j)));
            end
        end
        plot(uz,rr,'displayName',num2str(t))
    end  
    hold off
    grid on
    legend('-DynamicLegend','location','best')
    xlabel('u_\phi/\omegaR')
    ylabel('\rho/R')
    title('Perfil de velocidades')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end

Actividades

Se pulsa el botón titulado Nuevo para observar el estado transitorio y su evolución hacia el estado estacionario

Referencias

Tasos C. Papanastasiou, Georgios C. Georgiou, Andreas N. Alexandrou. Viscous Fluid Flow. CRC Press 2000. Sección 6.6

A. Salih. An Exact Solution of Navier–Stokes Equation. July 2011

Michel O. Deville. An Introduction to the Mechanics of Incompressible Fluids. Springer (2022), pp. 73-76