Supongamos un depósito cilíndrico de sección S, lleno de líquido de densidad ρ hasta una altura h₀ que se vacía a través de un tubo horizontal de diámetro D y longitud L, tal como se muestra en la figura.

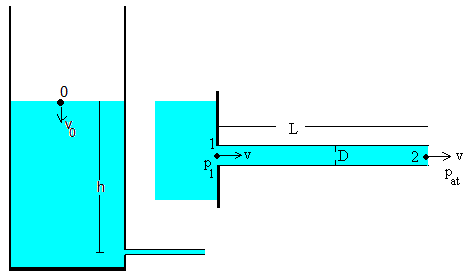
En el instante t, la altura del líquido en el depósito es h, aplicamos la ecuación de Bernoulli a los puntos 0 y 1 en el depósito.

${\displaystyle p_0+\rho g{y}_0+\frac{1}{2}\rho v_0^2=p_1+\rho g{y}_1+\frac{1}{2}\rho v_1^2}$

La diferencia de alturas y₀-y₁=h, la presión p₀ en la superficie del líquido en el depósito es la presión atmosférica p_at, y la velocidad v₀ es pequeña ya que la sección del recipiente S es mucho mayor que la sección del orificio de salida πD²/4.

${\displaystyle p_{at}+\rho gh=p_1+\frac{1}{2}\rho v_1^2}$     (1)

El volumen de líquido que sale en la unidad del tiempo del depósito es πD²v₁/4, es igual a razón de la variación del volumen S·h del depósito con el tiempo t cambiada de signo, ya que cuando sale líquido, su altura h en el depósito disminuye

${\displaystyle -S\frac{dh}{dt}=\pi \frac{D^2}{4}{v}_1}$

Consideremos ahora los extremos 1 y 2 del tubo capilar. Para un tubo horizontal de sección uniforme la ecuación de continuidad implica que v₁=v₂=v. Los puntos 1 y 2 están a la misma altura y₁=y₂, y la presión a la salida del tubo es la atmosférica p₂=p_at.

p₁-p_at=ρ(H_L+H_l)     (2)

Siendo H=H_L+H_l las pérdidas totales de carga.

Combinando las ecuaciones (1) y (2), llegamos a

${\displaystyle \rho gh=\rho \left(H_L+H_l\right)+\frac{1}{2}\rho v^2}$

• Otras pérdidas

Bajo el término H_l se agrupan otras pérdidas menores debidas a la entrada y salida del fluido por el tubo horizontal y que son independientes de que el régimen del fluido sea laminar o turbulento.

${\displaystyle H_l=k\frac{v^2}{2}}$

• Fluido en régimen laminar

A la diferencia de presión p₁-p₂ en los extremos del tubo horizontal dividida entre la densidad ρ del fluido, se le denomina pérdida de carga H_L en el flujo laminar

${\displaystyle H_L=\frac{p_1-p_2}{\rho }=\frac{8\eta L}{\rho \pi r^4}G=\frac{8\eta L}{\rho r^2}v=\frac{32\eta L}{\rho D^2}v}$

Llegamos a las ecuaciones

${\displaystyle \begin{array}{l}\rho gh=\rho \frac{k+1}{2}{v}^2+\frac{32\eta L}{D^2}v\\ -S\frac{dh}{dt}=\pi \frac{D^2}{4}v\end{array}}$

Solución de la ecuación diferencial

Resolvemos la ecuación diferencial en h

${\displaystyle \begin{array}{l}h=-\frac{1}{\gamma }\frac{dh}{dt}+\alpha {\left(\frac{dh}{dt}\right)}^2\\ \gamma =\frac{\pi D^4\rho g}{128\eta LS}\alpha =\frac{8(k+1)S^2}{g{\pi }^2{D}^4}\end{array}}$

con las condiciones iniciales en el instante t=0, h=h₀.

${\displaystyle \frac{dh}{dt}=\frac{1-\sqrt{1+4\alpha {\gamma }^{2}h}}{2\alpha \gamma }}$

como dh/dt<0, se toma la raíz negativa

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}z=\sqrt{1+4\alpha {\gamma }^{2}h}\\ \frac{dz}{dt}=\frac{4\alpha {\gamma }^2}{2\sqrt{1+4\alpha {\gamma }^{2}h}}\frac{dh}{dt}=\frac{2\alpha {\gamma }^2}{z}\frac{dh}{dt}\end{array}}$

Obtenemos la ecuación diferencial en z

${\displaystyle \frac{z}{z-1}\frac{dz}{dt}=-\gamma }$

que se integra fácilmente

${\displaystyle \begin{array}{l}{\displaystyle \underset{z_0}{\overset{z}{\int }}\left(1+\frac{1}{z-1}\right)}dz=-\gamma {\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ \ln \left(z-1\right)+\ln z-\ln \left(z_0-1\right)+\ln z_0=-\gamma t\\ \left(z-1\right)e^{z-1}=\left(z_0-1\right)e^{z_0-1-\gamma t}\end{array}}$

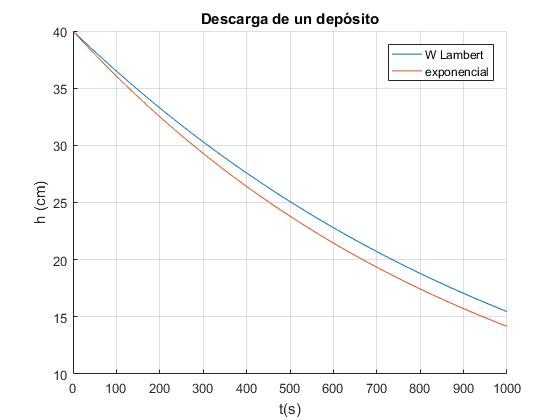
Expresamos la solución en términos de la función W de Lambert

${\displaystyle z(t)=W((z_0-1)e^{z_0-1-\gamma t})+1}$

con

${\displaystyle z_0=\sqrt{1+4\alpha {\gamma }^2{h}_0}}$

La altura h del líquido en el recipiente es

${\displaystyle \begin{array}{l}h(t)=\frac{1}{4\alpha {\gamma }^2}\left\{{\left(1+W\left(\beta e^{\beta -\gamma t}\right)\right)}^2-1\right\}\\ \beta =z_0-1\end{array}}$

Como β>0 la solución se encuentra en la rama W₀(x)

Teniendo en cuenta que W(βe^β)=β, verificamos que se satisfacen las condiciones iniciales en el instante t=0, h=h₀

Aproximaciones

El desarrollo en serie de W₀(x) es útil cuando precisamos valores de la función W de Lambert cerca de x=0

${\displaystyle W(x)={\displaystyle \sum _{n=1}^{\infty }\frac{{(-n)}^{n-1}}{n!}}{x}^n}$

syms x;
>> taylor(lambertw(0, x))
ans =(125*x^5)/24 - (8*x^4)/3 + (3*x^3)/2 - x^2 + x
taylor(sqrt(1+x))
ans =(7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + x/2 + 1

Cuando x es pequeño W₀(x)≈x y $\sqrt{1+x}\approx 1+\frac{1}{2}x$

${\displaystyle h(t)\approx \frac{1}{4\alpha {\gamma }^2}\left\{{\left(1+\beta e^{\beta -\gamma t}\right)}^2-1\right\}\approx \frac{2\beta e^{-\gamma t}}{4\alpha {\gamma }^2}\approx h_0{e}^{-\gamma t}}$

La altura h del fluido en el recipiente decrece exponencialmente con el tiempo

Ejemplo

Un depósito de 4 cm de diámetro, contiene agua (densidad ρ=1000 kg/m³ viscosidad η=0.922·10^-3 Pa·s) hasta una altura h₀=40 cm, se vacía a través de un tubo capilar D=1 mm de diámetro y L=19.8 cm de longitud. Tomamos un valor de k=1.78.

%Datos
S=pi*0.02^2; %sección del depósito
h0=0.4; %altura inicial de agua
L=0.2; %longitud del capilar
D=0.001; %diámetro del capilar
eta=0.922e-3; %viscosidad del agua
k=1.78; %coeficiente de pérdidas

alfa=8*(k+1)*S^2/(9.8*pi^2*D^4);
gamma=pi*D^4*1000*9.8/(128*eta*L*S);
beta=sqrt(1+4*alfa*gamma^2*h0)-1;

h=@(t) ((1+lambertw(0,beta*exp(beta-gamma*t))).^2-1)*100/(4*alfa*gamma^2);
hh=@(t) h0*exp(-gamma*t)*100;
hold on
fplot(h,[0,1000])
fplot(hh,[0,1000])
hold off
grid on
legend('W Lambert','exponencial')
xlabel('t(s)')
ylabel('h (cm)')
title('Descarga de un depósito')

Número de Reynolds

La máxima velocidad del líquido en el tubo-capilar se produce en el instante t=0, cuando h=h₀

${\displaystyle \begin{array}{l}{\left(\frac{dh}{dt}\right)}_{t=0}=\frac{1-\sqrt{1+4\alpha {\gamma }^2{h}_0}}{2\alpha \gamma }\\ v_{máx}=-\frac{4S}{\pi D^2}{\left(\frac{dh}{dt}\right)}_{t=0}\end{array}}$

El número de Reynolds es $\mathrm{Re}=\frac{\rho Dv}{\eta }$

>> dh=(1-sqrt(1+4*alfa*gamma^2*h0))/(2*alfa*gamma);
>> v=-4*S*dh/(pi*D^2)
v =    0.5840
>> Re=1000*D*v/eta
Re =  633.3862

Un número de Reynolds Re=633 es indicativo de un fluido en régimen laminar

Medida de la viscosidad del agua

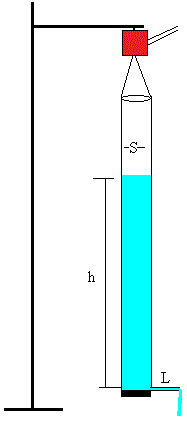
Diseñamos una experiencia para medir la viscosidad del agua con con un tubo-capilar. Podemos medir la altura de la columna de líquido en función del tiempo directamente, pero es mejor colgar el tubo-capilar vacío de un sensor de fuerza y tararlo a cero. Se llena el tubo de agua hasta una altura h₀, se deja fluir el agua a través del capilar, el sensor mide la masa m(t) de agua en el tubo-capilar en función del tiempo. La altura del fluido es h(t)=m(t)/(ρS), siendo ρ la densidad del agua y S la sección del tubo.

En esta experiencia simulada, introducimos

• La longitud L del capilar en cm, en el control titulado Longitud capilar

• La altura inicial h₀ de agua en el tubo en cm, en el control titulado Altura inicial

El programa interactivo ha fijado los siguientes parámetros

• La viscosidad del agua es un número aleatorio entre 0.9 y 1·10^-3 Pa·s, que tendremos que determinar
• El parámetro k de otras pérdidas, es un número aleatorio, comprendido entre 1.16 y 1.76
• La densidad del agua ρ=998 kg/m³
• La sección del tubo S=1.293·10^-3 m²
• El diámetro del capilar, D=1 mm

El programa calcula la altura h del agua en función del tiempo t, utilizando la función W de Lambert dependiente de los parámetros, α, β y γ.

${\displaystyle \begin{array}{l}h(t)=\frac{1}{4\alpha {\gamma }^2}\left\{{\left(1+W\left(\beta e^{\beta -\gamma t}\right)\right)}^2-1\right\}\\ \gamma =\frac{\pi D^4\rho g}{128\eta LS},\alpha =\frac{8(k+1)S^2}{g{\pi }^2{D}^4},\beta =\sqrt{1+4\alpha {\gamma }^2{h}_0}-1\end{array}}$

En la parte derecha, se nos proporciona los datos de la altura h del agua en el tubo medida cada 100 s. A partir de estos datos, mediremos la viscosidad η del agua

En una primera aproximación, supondremos que la altura h del agua en el tubo decrece exponecialmente con el tiempo, h=h₀exp(-γt) o bien,

lnh=lnh₀-γt, que es la ecuación de una recta de pendiente -γ

Ejemplo, en el programa interactivo, establecemos

• La longitud L=10 cm del capilar
• La altura inicial h₀=50 cm de agua en el tubo

Representamos en el eje horizontal los tiempos y en el vertical lnh.

t=0:100:1100;
h=[50.0,43.6,37.8,32.7,28.2,24.1,20.6,17.6,14.9,12.6,10.7,9.0];
plot(t,log(h),'ro','markersize',3,'markerfacecolor','r')
title('Ajuste lineal')
xlabel('t')
ylabel('ln(h)')
grid on

En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.

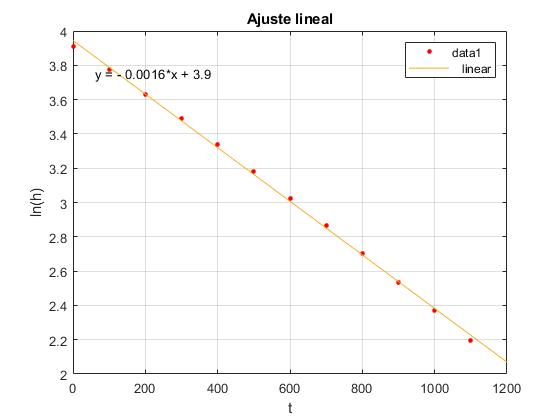
El parámetro γ (pendiente de la recta) es el valor del coeficiente p1=0.0015629. Conocido γ, despejamos la viscosidad del agua η

>> pi*0.001^4*998*9.8/(0.0015629*128*0.1*1.293e-3)
ans =    0.0012

Difiere del valor que se había generado en el programa interactivo, η=0.000984 Pa·s

Referencias

Rafael M. Digilov. Gravity discharge vessel revisited: An explicit Lambert W function solution. Am. J. Phys. 85 (7) July 2017, pp. 510-514

La aplicación HTML5-canvas contiene la implementación de la función W de Lambert en javascript que se ha tomado de la página web https://github.com/protobi/lambertw. 2015 Pieter Sheth-Voss. Version 3, 29 June 2007