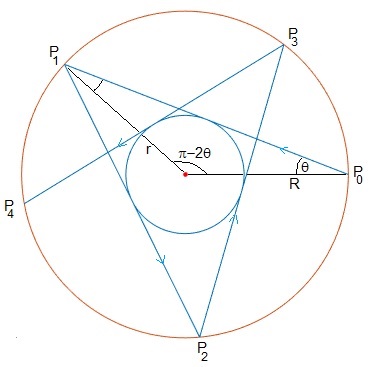
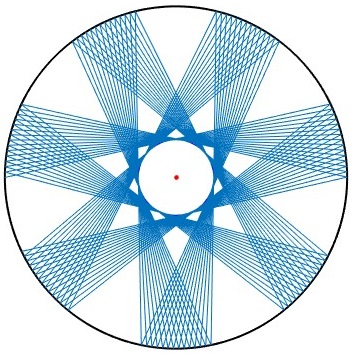
En la figura, se muestra un rayo de luz que entra por un orificio situada en la posición P₀, (R,0) haciendo un ángulo θ con el eje X. Se releja en la posición P₁, el ángulo que forma el rayo incidente con la dirección radial es igual al ángulo que forma el rayo reflejado con la dirección radial e igual ángulo θ. Después de relejarse en P₁ el rayo se refleja en P₂ y así, sucesivamente.

La distancia de la recta que pasa por P₀ y P₁ al origen es r=Rsinθ. Un círculo de radio r es la región oscura, donde no penetra la luz, ya que los rayos son tangentes a esta circunferencia concéntrica.

Los puntos P₀, P₁, P₂, P₃... pueden representarse en notación compleja z=Rexp(iθ)

Partimos del punto P₀. La posición angular del punto P₁ es π-2θ. La posición angular del punto P₂ es 2(π-2θ), la posición angular del punto P_k es k(π-2θ)

${\displaystyle \begin{array}{l}{z}_k=R\exp \left(ik\left(\pi -2\theta \right)\right)=R\exp \left(ik\pi \right)\exp \left(-2ik\theta \right)=\\ R\left(\cos \left(k\pi \right)+i\sin \left(k\pi \right)\right)\left(\cos \left(-2k\theta \right)+i\sin \left(-2k\theta \right)\right)=\\ {\left(-1\right)}^{k}R\left(\cos \left(2k\theta \right)-i\sin \left(2k\theta \right)\right)\\ \{\begin{array}{l}{x}_0=-R,y_0=0\\ x_1=-R\cos \left(2\theta \right),y_1=R\sin \left(2\theta \right)\\ \mathrm{...}\\ x_k={\left(-1\right)}^{k}R\cos \left(2k\theta \right),y_k=-{\left(-1\right)}^{k}R\sin \left(2k\theta \right)\end{array}\end{array}}$

Para que la trayectoria sea cerrada los puntos coinciden, P_n=P₀

${\displaystyle \begin{array}{l}{z}_n=z_0\\ R\exp \left(in\left(\pi -2\theta \right)\right)=R\\ R\exp \left(in\left(\pi -2\theta \right)\right)=R\exp \left(2ik\pi \right)\\ n\left(\pi -2\theta \right)=2k\pi \\ \theta =\left(\frac{1}{2}-\frac{k}{n}\right)\pi \\ \theta >\mathrm{0,}k<\frac{n}{2}\end{array}}$

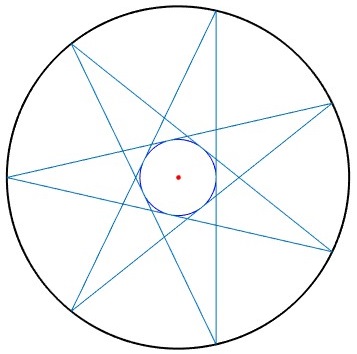
Ejemplos

Trayectoria cerrada

R=1; %radio exterior
k=3; %menor que n/2
n=7;
th=(1/2-k/n)*pi;
r=R*sin(th); %radio interior
x1=R; y1=0;
hold on
fplot(@(t) r*cos(t), @(t) r*sin(t),[0,2*pi])
fplot(@(t) R*cos(t), @(t) R*sin(t),[0,2*pi], 'k','lineWidth',1.5)
plot(0,0,'ro','markersize',3,'markerfacecolor','r')
for k=1:n
    x2=(-1)^k*R*cos(2*k*th);
    y2=-(-1)^k*R*sin(2*k*th);
    line([x1,x2],[y1,y2])
    x1=x2;    y1=y2;
end
axis equal
axis off
hold off

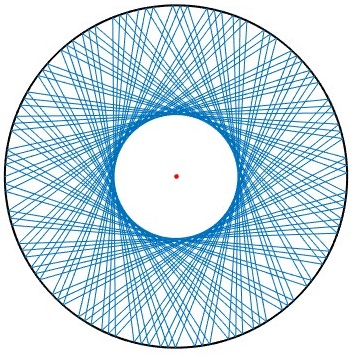
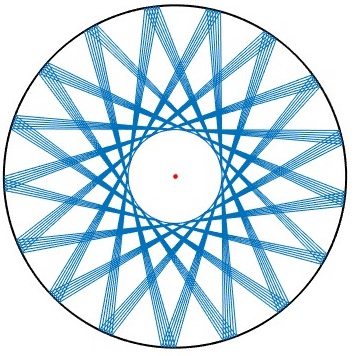
Otros ejemplos

Se representan 100 reflexiones, para tres ángulos $\theta =\frac{\pi }{6\sqrt{2}},\frac{\pi }{8\sqrt{2}},\frac{\pi }{10\sqrt{2}}$

R=1; %radio
th=pi/(6*sqrt(2));
x1=R; y1=0;
hold on
fplot(@(t) R*cos(t), @(t) R*sin(t),[0,2*pi], 'k','lineWidth',1.5)
plot(0,0,'ro','markersize',3,'markerfacecolor','r')
for k=1:100
    x2=(-1)^k*R*cos(2*k*th);
    y2=-(-1)^k*R*sin(2*k*th);
    line([x1,x2],[y1,y2])
    x1=x2;    y1=y2;
end
axis equal
axis off
hold off

Lente cilíndrica

Sea una lente de vidrio transparente de índice de refracción n de forma de semicilíndica de radio R.

Un rayo incide en la posición x₀ con un ángulo α respecto a la normal a la superficie horizontal, el rayo se refracta en la superficie horizontal formando un ángulo β con dicha dirección. Suponiendo que el aire tiene índice de refracción 1, la ley de Snell para la refracción en la superficie horizontal, se escribe

sinα=n·sinβ

• Rayo incidente a la derecha del origen, x₀>0



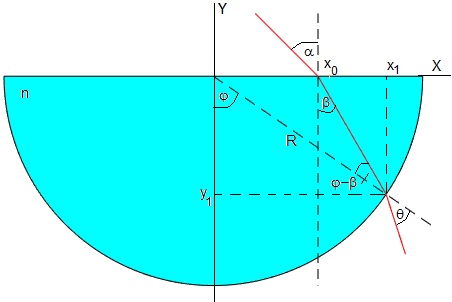
El rayo refractado, llega a la superficie cilíndrica formando un ángulo φ-β con la dirección radial (normal a la superficie cilíndrica), la ley de Snell se escribe

n·sin(φ-β)=sinθ

siendo θ>φ-β el ángulo que forma el rayo refractado con dicha dirección.



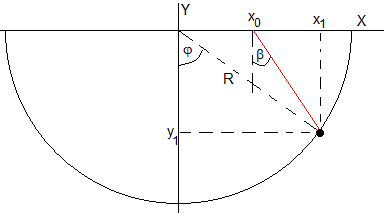
El ángulo φ se calcula a partir de consideraciones geométricas. El punto P de coordenadas (x₁, y₁) es la intersección de la recta que pasa por el punto (x₀,0) que forma un ángulo 90+β con el eje X, y la circunferencia de centro en el origen y radio R.

${\displaystyle \{\begin{array}{l}y=\frac{x_0-x}{\tan \beta }\\ x^2+y^2=R^2\end{array}}$

Resolvemos el sistema de dos ecuaciones para calcular el punto de intersección (x₁, y₁)

${\displaystyle \begin{array}{l}\frac{x^2}{{\sin }^2\beta }-2\frac{x_0}{{\tan }^2\beta }x+\frac{x_0^2}{{\tan }^2\beta }-R^2=0\\ x_1=x_0{\cos }^2\beta +\sin \beta \sqrt{R^2-x_0^2{\cos }^2\beta }\\ y_1=\frac{x_0-x_1}{\tan \beta }\end{array}}$

El ángulo φ es

${\displaystyle \tan \phi =\frac{x_1}{-y_1}=\frac{x_1\tan \beta }{x_1-x_0}=\frac{x_0\cos \beta +\tan \beta \sqrt{R^2-x_0^2{\cos }^2\beta }}{-x_0\sin \beta +\sqrt{R^2-x_0^2{\cos }^2\beta }}}$

Reflexión total



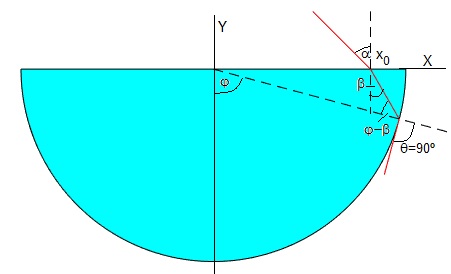
Calcularemos la posición x₀ para el cual el ángulo θ=90°, el rayo refractado que sale de la lente cilíndrica es tangente a la superficie cilíndrica, se produce la reflexión total.

n·sin(φ-β)=1

Dado el ángulo φ=arcsin(1/n)+β, obtenemos x₁=Rsin(φ), y₁=-Rcos(φ). A partir de la relación

${\displaystyle y_1=\frac{x_0-x_1}{\tan \beta }}$

calculamos, x₀=Rsin(φ)-Rcos(φ)tan(β)

• Rayo incidente en el origen, x₀=0



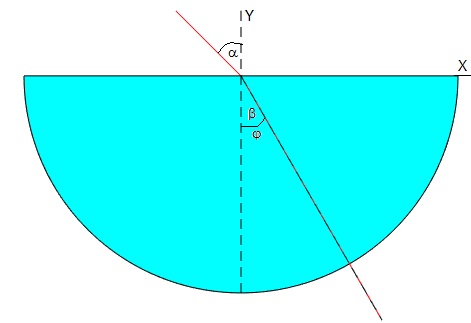
Consideramos el rayo que pasa por el origen, x₀=0

x₁=Rsin(β), y₁=-Rcos(β), tanφ=tanβ. El ángulo de incidencia del rayo refractado sobre la superficie cilíndrica φ-β=0, el rayo tiene la dirección radial y no se desvía.

Este es el caso que estudiaremos en el siguiente apartado titulado 'Práctica de laboratorio'

• Rayo incidente a la izquierda del origen, x₀<0



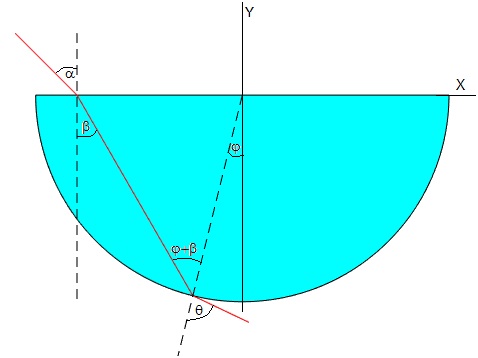
El rayo refractado, llega a la superficie cilíndrica formando un ángulo φ+β con la dirección radial (normal a la superficie cilíndrica), la ley de Snell para la refracción en la superficie cilíndrica, se escribe

n·sin(φ+β)=sinθ

siendo θ>φ+β el ángulo que forma el rayo refractado con dicha dirección.

Reflexión total

Consideramos la posición x₀ para el cual el ángulo θ=90°, el rayo refractado que sale de la lente cilíndrica es tangente a la superficie cilíndrica, se produce la reflexión total.

n·sin(φ+β)=1

Dado el ángulo φ=arcsin(1/n)-β, calculamos x₁=-Rsin(φ), y₁=-Rcos(φ). A partir de la relación

${\displaystyle y_1=\frac{x_0-x_1}{\tan \beta }}$

calculamos x₀=-Rsin(φ)-Rcos(φ)tan(β)

Ejemplo

• Radio de la lente semicircular, R=1
• Indice de refracción del vidrio, $n=\sqrt{2}$
• Angulo de incidencia medido desde la normal a la superficie plana, α=45°

Calculamos los ángulos φ para los que se produce la reflexión total

Refracción en la superficie plana, sinα=n·sinβ, β=30°

• para x₀>0

Refracción en la superficie cilíndrica, el ángulo φ=arcsin(1/n)+β=45°+30°=75°

La posición x₀=Rsin(75)-Rcos(75)tan(30)=$R\sqrt{6}/3$

• para x₀<0

Refracción en la superficie cilíndrica, el ángulo φ=arcsin(1/n)-β=45°-30°=15°

La posición x₀=-Rsin(15)-Rcos(15)tan(30)=$-R\sqrt{6}/3$

Para representar las figuras de este apartado, se ha creado el siguiente script de MATLAB

n=sqrt(2); %índice de refracción
alfa=pi/4; %ángulo incidente
R=1; %radio
beta=asin(sin(alfa)/n);
phi_m=asin(sin(alfa)/n)+asin(1/n); %ángulo límite
t=linspace(pi, 2*pi, 100);
x=R*cos(t);
y=R*sin(t);
x=[x,x(1)];
y=[y,y(1)];
fill(x,y,'c')

xm=R*sin(phi_m)-R*cos(phi_m)*tan(beta); %reflexión total
x0=0.5; %posición
line([x0-0.3, x0],[0.3/tan(alfa),0],'color','r')
x1=x0*cos(beta)^2+sin(beta)*sqrt(R^2-(x0*cos(beta))^2);
y1=(x0-x1)/tan(beta);
line([x0,x1],[0,y1],'color','r')
line([x0,x0],[0.3,-1],'color','k','lineStyle','--')
phi=atan(x1/(-y1));
if abs(x0)<=xm %refracción
    th=asin(n*sin(phi-beta));
    x2=x1-0.3*sin(th-phi);
    y2=y1-0.3*cos(th-phi);
    line([x1,x2],[y1,y2],'color','r')
    line([0,(R+0.3)*sin(phi)],[0,-(R+.3)*cos(phi)],'color','k','lineStyle','--')
else %reflexión
    x2=x1-0.3*sin(2*phi-beta);
    y2=y1+0.3*cos(2*phi-beta);
    line([x1,x2],[y1,y2],'color','r')
    line([0,(R+0.3)*sin(phi)],[0,-(R+.3)*cos(phi)],'color','k','lineStyle','--')
end
axis off
axis equal

Referencias

R De Luca. The path of a light ray in a semicircular cavity. Phys. Educ. 58 (2023) 065018