Indice de refracción

El índice de refracción n no es constante, sino que depende de la longitud de onda o de la frecuencia de la luz con la que se ilumina la lente.

Por ejemplo, el índice de refracción del vidrio denominado “corona pesado” para las longitudes de onda del espectro visible, se proporcionan en la siguiente tabla.

Fuente: Koshkin N. I., Shirkévich M. G.. Manual de Física Elemental. Editorial Mir 1975. pág. 210

x=[670.8,643.8, 589.3,486.4,404.7];  %longitud de onda en nm
y=[1.6434,1.6453,1.6499,1.6637,1.6852]; %índice de refracción
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
xlabel('\lambda (nm)')
ylabel('n')
title('Indice de refracción del vidrio')

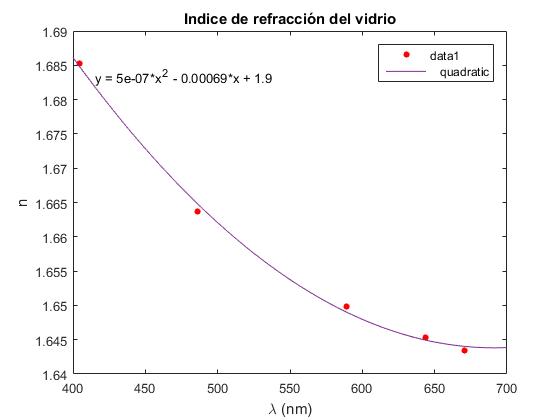
Seleccionamos en el menú de la ventana gráfica que aparece Tools/Basic fitting. Probamos primero el ajuste lineal (linear), luego el ajuste a un polinomio de grado dos (quadratic), a un polinomio de grado tres (cubic).

En la figura, se muestra los datos de la tabla representados por puntos de color rojo y el polinomio de segundo grado, que mejor ajusta a dichos datos. (Cunado se intenta ajustar a un polinomio de tercer grado, se recibe un mensaje de advertencia).

n=1.8822-6.8978·10^-4·λ+4.9894·10^-7·λ²

Los rayos inciden sobre la superficie plana

Un rayo de luz monocromática de longitud de onda λ paralelo al eje X incide en una lente esférica de radio R. El rayo incide en la dirección normal y no se desvía, llega al punto P de la superficie esférica de separación entre la lente y el aire, su ángulo de incidencia es α, el ángulo de refracción es β. Aplicamos la ley de Snell

n·sinα=sinβ

n es el índice de refracción de la lente para la longitud de onda λ. El índice de refracción del aire es la unidad.

Vamos a calcular la posición de la intersección F del rayo refractado con el eje de simetría X, es decir, la distancia f del punto F al punto O.

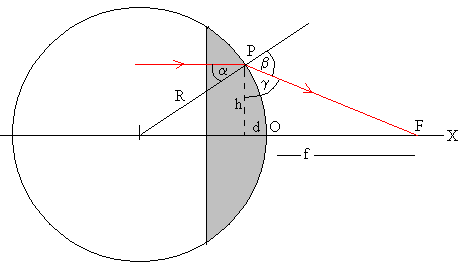
De acuerdo con la geometría del problema

${\displaystyle \begin{array}{l}\sin \alpha =\frac{h}{R}d=R-\sqrt{R^2-h^2}\\ \sin \beta =\sin \left(\frac{\pi }{2}+\alpha -\gamma \right)=\sin \left(\frac{\pi }{2}-(\gamma -\alpha )\right)=\cos \left(\gamma -\alpha \right)\\ \sin \beta =\cos \gamma \cos \alpha +\sin \gamma \sin \alpha \\ n\sin \alpha =\frac{h}{\sqrt{{\left(f+d\right)}^2+h^2}}\cos \alpha +\frac{f+d}{\sqrt{{\left(f+d\right)}^2+h^2}}\sin \alpha \\ n\frac{h}{R}=\frac{h}{\sqrt{{\left(f+d\right)}^2+h^2}}\frac{\sqrt{R^2-h^2}}{R}+\frac{f+d}{\sqrt{{\left(f+d\right)}^2+h^2}}\frac{h}{R}\\ n\sqrt{{\left(f+d\right)}^2+h^2}=\sqrt{R^2-h^2}+f+d\end{array}}$

Elevamos ambos miembros al cuadrado y despejamos f en función de h

${\displaystyle f=\frac{n\sqrt{R^2-n^2{h}^2}-\left(n^2-1\right)R+n^2\sqrt{R^2-h^2}}{n^2-1}}$

n=1.5; %índice de refracción
t=1; %espesor
R=4; %radio
hold on
alfa=acos((R-t)/R);
ang=linspace(-alfa,alfa,100);
x=R*cos(ang);
y=R*sin(ang);
fill([x(1),x(2:end),x(1)],[y(1),y(2:end),y(1)],'c')
for h=linspace(-2.5,2.5,10)
    line([0,sqrt(R^2-h^2)],[h,h],'color','b')
    f=(n*sqrt(R^2-n^2*h^2)-(n^2-1)*R+n^2*sqrt(R^2-h^2))/(n^2-1);
    line([sqrt(R^2-h^2),R+f],[h,0],'color','b')
end 
line([0,10],[0,0],'color','k')
hold off
grid on
axis equal
axis off    

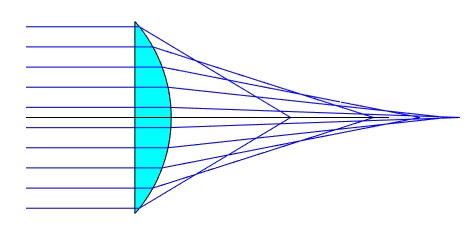
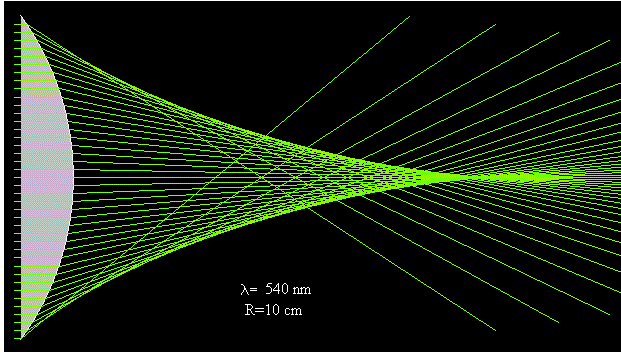
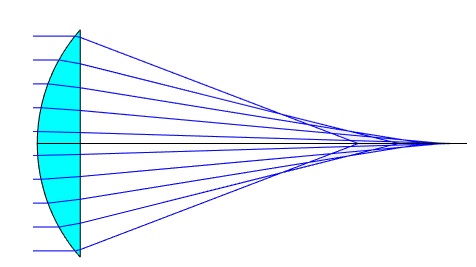
En la figura observamos el trazado de rayos para una lente esférica de radio R=4 cm y espesor máximo 1 cm. la intersección del rayo refractado con el eje X nos da la posición del foco

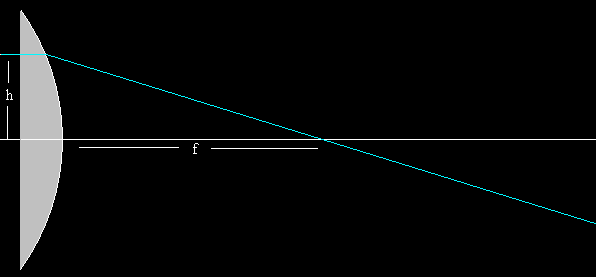
f₀ no depende de h, esto quiere decir que todos los rayos paralelos al eje convergen en el mismo punto F₀ denominado foco.

El ángulo α y por tanto h tienen un valor límite, aquél que hace que β=90º.

${\displaystyle n·\sin \alpha =1h_{\lim }=\frac{R}{n}}$

Para h>h_lim el rayo incidente no se refracta sino que experimenta una reflexión interna.

La expresión de f calculada anteriormente es válida para el intervalo (-h_lim, +h_lim). El valor máximo de h, h_máx de la lente con la experimentaremos al final de esta página cumple que h_max<h_lim, de modo que todos los rayos incidentes se refractan.

La distancia focal mínima  f_min se obtiene cuando h=h_max. Y la distancia focal máxima, se obtiene cuando h→0, es decir, f₀, la distancia focal en la aproximación paraxial.

Representamos la distancia focal f en función de h hasta h_máx=R/n para dos radios de la lente R=5 cm, y R=7.5 cm

n=1.5; %índice de refracción
hold on
for R=[5,7.5]
    f=@(x) (n*sqrt(R^2-n^2*x.^2)-(n^2-1)*R+n^2*sqrt(R^2-x.^2))/(n^2-1);
    fplot(f,[0,R/n],'displayName',num2str(R))
end
hold off
legend('-DynamicLegend','location','northeast')
grid on
xlabel('h(cm)')
ylabel('f(cm)')
title('Distancia focal')

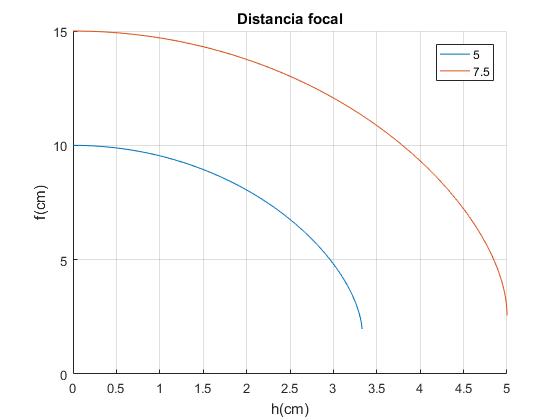
Aproximación paraxial se obtiene cuando h→0

${\displaystyle f_0=\frac{R}{n-1}}$

Cuando incide luz blanca sobre la lente esférica, las rayos monocromáticos (violeta, azul, verde, amarillo, naranja, rojo) experimentan desviaciones distintas, debido a que el índice de refracción de la lente cambia ligeramente con la longitud de onda. La mayor dispersión, separación de colores, se obtiene para h_max.

La superficie cáustica

Situamos el origen en el punto O. El rayo refractado pasa por los puntos P de coordenadas (-d, h) y el punto F (f, 0). La ecuación de la recta que pasa por estos dos puntos es

${\displaystyle \begin{array}{l}y=-\frac{h}{d+f}(x-f)\\ y=-\frac{h}{R-\sqrt{R^2-h^2}+f}(x-f)\end{array}}$

La envolvente de estas rectas se denomina cáustica y su ecuación se determina haciendo

${\displaystyle \begin{array}{l}\frac{\partial y(x,h)}{\partial h}=0\\ \frac{\partial y(x,h)}{\partial h}=-\frac{\left(f+R-\sqrt{R^2-h^2}\right)-\left(\frac{\partial f}{\partial h}+\frac{h}{\sqrt{R^2-h^2}}\right)h}{{\left(f+R-\sqrt{R^2-h^2}\right)}^2}(x-f)-\frac{h}{f+R-\sqrt{R^2-h^2}}\left(-\frac{\partial f}{\partial h}\right)=0\\ x=f+\left(\frac{\partial f}{\partial h}\right)\frac{f+R-\sqrt{R^2-h^2}}{f+R-\sqrt{R^2-h^2}-h\frac{\partial f}{\partial h}+\frac{h}{\sqrt{R^2-h^2}}}\end{array}}$

No se puede obtener una ecuación explícita y=g(x) de la cáustica. Sus ecuaciones paramétricas dependiendo de h, o altura del rayo son:

${\displaystyle \begin{array}{l}y=-\frac{h}{R-\sqrt{R^2-h^2}+f}(x-f)\\ x=f+\left(\frac{\partial f}{\partial h}\right)\frac{f+R-\sqrt{R^2-h^2}}{f+R-\sqrt{R^2-h^2}-h\frac{\partial f}{\partial h}+\frac{h}{\sqrt{R^2-h^2}}}\\ f=\frac{n\sqrt{R^2-n^2{h}^2}-\left(n^2-1\right)R+n^2\sqrt{R^2-h^2}}{n^2-1}\\ \frac{\partial f}{\partial h}=-\frac{n^{2}h}{n^2-1}\left(\frac{n}{\sqrt{R^2-n^2{h}^2}}+\frac{h}{\sqrt{R^2-h^2}}\right)\end{array}}$

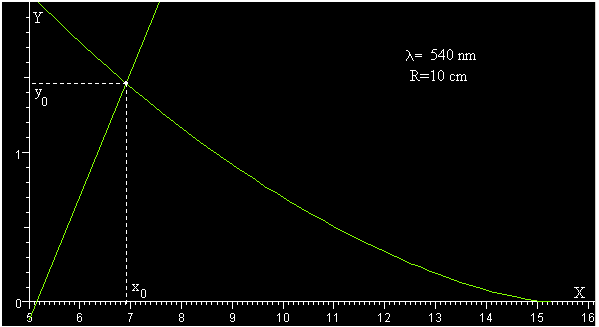
La imagen que vemos en la figura más arriba nos dice que los rayos paralelos no convergen en el mismo punto F₀ denominado foco. Si ponemos una pantalla después de la lente perpendicularmente al eje X en la posición x, observaremos una mancha de luz de radio finito.

Punto focal óptimo

El punto focal óptimo se define como el punto x₀ donde se tiene que colocar la pantalla para que se observe una mancha de radio mínimo y₀. Se obtiene de la intersección de la cáustica con el rayo procedente de –h_max, véase la figura más arriba.

Para ello, se determina el valor de h tal que la ordenada y de la cáustica y la ordenada del rayo trazado desde -h_max coinciden.

${\displaystyle \frac{h}{R-\sqrt{R^2-h^2}+f}(x-f)=\frac{-h_{\max }}{R-\sqrt{R^2-h_{\max }^2}+f_{\min }}(x-f_{\min })}$

Donde x es la abscisa de la caústica que hemos definido previamente en términos de f y su derivada. f_min es la distancia focal mínima cuando h es máximo.

${\displaystyle \{\begin{array}{l}x=f+\left(\frac{\partial f}{\partial h}\right)\frac{f+R-\sqrt{R^2-h^2}}{f+R-\sqrt{R^2-h^2}-h\frac{\partial f}{\partial h}+\frac{h}{\sqrt{R^2-h^2}}}\\ f=\frac{n\sqrt{R^2-n^2{h}^2}-(n^2-1)R+n^2\sqrt{R^2-h^2}}{n^2-1}\\ \frac{\partial f}{\partial h}=-\frac{n^{2}h}{n^2-1}\left(\frac{n}{\sqrt{R^2-n^2{h}^2}}+\frac{h}{\sqrt{R^2-h^2}}\right)\end{array}}$

Como vemos en la figura, la cáustica decrece con x y la recta que sigue el rayo crece con x. La intersección se produce en el punto (x₀, y₀). Los ejes X e Y se han trazado a distinta escala para que se pueda apreciar mejor la recta y la cáustica. El punto focal óptimo se encuentra en x₀ y el tamaño de la mancha de luz es un círculo de radio y₀.

Se utiliza la función fzero de MATLAB para obtener el valor de h₀ raíz de la ecuación transcendente. Después se determina la abscisa x₀ y la ordenada y₀ en la ecuación de la cáustica. La curva de color azul es la caústica y la de color anaranjado es la recta que parte de -h_máx. Se han señalado mediante líneas a trazos, la abscisa x₀ y la ordenada y₀

n=1.5; %índice de refracción
R=10; %radio
hm=3; 

f=@(h)(n*sqrt(R^2-n^2*h.^2)-(n^2-1)*R+n^2*sqrt(R^2-h.^2))/(n^2-1);
Df_h=@(h) -n^2*h.*(n./sqrt(R^2-n^2*h.^2)+h./sqrt(R^2-h.^2))/(n^2-1);
x=@(h) f(h)+Df_h(h).*(f(h)+R-sqrt(R^2-h.^2))./(f(h)+R-sqrt(R^2-h.^2)-
h.*Df_h(h)+h./sqrt(R^2-h.^2));
g=@(h) h.*(x(h)-f(h))./(R-sqrt(R^2-h.^2)+f(h))+hm*(x(h)-f(hm))/
(R-sqrt(R^2-hm^2)+f(hm));

h0=fzero(g,[0,hm]);

hold on
y=@(h) -h.*(x(h)-f(h))./(R-sqrt(R^2-h.^2)+f(h));
r=@(x) hm*(x-f(hm))/(f(hm)+R-sqrt(R^2-hm^2));
fplot(x,y,[0,hm])
fplot(r,[0,f(hm)+2])
line([x(h0),x(h0)],[0,y(h0)],'lineStyle','--','color','k')
line([0,x(h0)],[y(h0),y(h0)],'lineStyle','--','color','k')
plot(x(h0),y(h0),'ko','markersize',4,'markeredgecolor','k',
'markerfacecolor','k')
hold off
grid on
ylim([0,0.2])
xlabel('x')
ylabel('y')
title('Punto focal óptimo')

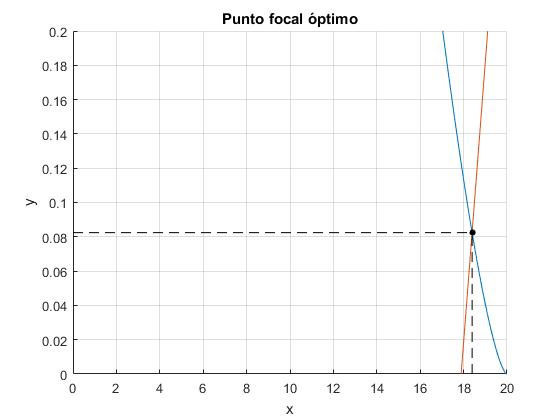
>> x(h0)
ans =   18.3914
>> y(h0)
ans =    0.0824

Actividades

Se introduce

• El radio R de la lente esférica en cm, actuando en la barra de desplazamiento titulada Radio.

Se pulsa el botón titulado Nuevo

• Seleccionamos la longitud de onda y por tanto, el índice de refracción n de la lente, en el control titulado Longitud de onda.
• Seleccionamos la altura h del rayo incidente sobre el eje de simetría X, en el control titulado Posición rayo .

En la parte superior se nos proporciona la distancia focal f entre el origen y el punto de intersección del rayo con el eje X.

Una marca sobre el eje horizontal nos proporciona el dato de la distancia focal máxima f₀, o distancia focal en la aproximación paraxial, cuando h→0

El máximo valor de la distancia del rayo al eje horizontal es h_max=5.85 cm, por debajo del valor límite R/n de modo, que los rayos no sufren en ningún caso reflexión total.

Los rayos inciden sobre la superficie esférica

Estudimaos ahora, la situación en la que los rayos paralelos al eje X inciden sobre la superficie esférica

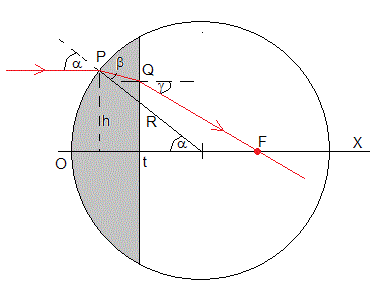
Un rayo de luz monocromática de longitud de onda λ paralelo al eje X incide en una lente esférica de radio R. El rayo incide formando un ángulo α con la dirección normal, se refracta en el punto (R-Rcosα, Rsinα) de la superficie esférica, formando un ángulo β,

sinα=n·sinβ

llega a la superficie plana. La ecuación de la dirección del rayo refractado, la recta que pasa por los puntos P y Q es

y-Rsinα=-tan(α-β)(x-R+Rcosα)

La intersección con la recta vertical x=t nos da la ordenada del punto Q

y_Q=Rsinα-tan(α-β)(x-R+Rcosα)

El rayo se refracta en Q

n·sin(α-β)=sinγ

La dirección del rayo refractado en Q corta al eje X en el punto F. La ecuación de la dirección del rayo refractado en Q es

(y-y_Q)=-(x-t)tanγ

La intersección con el eje X, y=0, nos da la abscisa x. Denominaremos f a la diferencia x-t

${\displaystyle f=\frac{R\sin \alpha +\tan \left(\alpha -\beta \right)(t-R+R\cos \alpha )}{\tan \gamma }}$

Creamos un script para dibujar los rayos de luz que atraviesan una lente de vidrio de 4 cm de radio

n=1.5; %índice de refracción
t=1; %espesor
R=4; %radio
hold on
alfa=acos((R-t)/R);
ang=linspace(-alfa,alfa,100);
x=R-R*cos(ang);
y=R*sin(ang);
fill([x(1),x(2:end),x(1)],[y(1),y(2:end),y(1)],'c')
for h=linspace(-2.5,2.5,10)
    alfa=asin(h/R);
    line([-0.1,R-R*cos(alfa)],[h,h],'color','b')
    beta=asin(sin(alfa)/n);
    line([R-R*cos(alfa), t],[h,R*sin(alfa)-tan(alfa-beta)*(t-R+R*cos(alfa))],
'color','b')
    gamma=asin(n*sin(alfa-beta));
    line([t,(tan(gamma)*t+R*sin(alfa)+tan(alfa-beta)*(t-R+R*cos(alfa)))
/tan(gamma)],[R*sin(alfa)-tan(alfa-beta)*(t-R+R*cos(alfa)),0],'color','b')
end 
line([0,10],[0,0],'color','k')
hold off
grid on
axis equal
axis off

Referencias.

Carpena P. Coronado A. V., On the focal point of a lens: beyond the paraxial approximation. Eur. J. Phys. 27 (2006) pp. 231-241