Imágenes virtuales de un objeto situado entre dos espejos planos

Reflexión en espejos planos

Un espejo plano

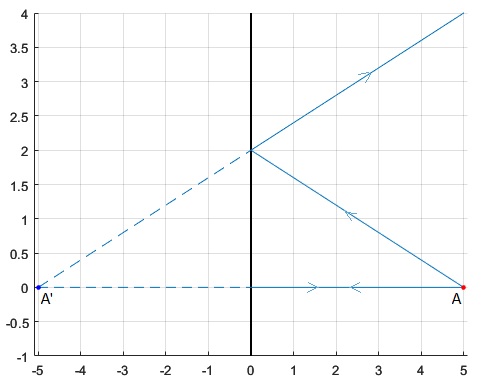
El caso más sencillo, es la determinación de la posición de la imagen virtual A' de un objeto puntual A situado frente a un espejo plano

line([0,0],[-1,4], 'LineWidth', 1.5, 'color','k')
line([-5,0],[0,0], 'lineStyle','--')
line([5,0],[0,0])
line([-5,0],[0,2],'lineStyle','--')
line([0,5],[2,4])
line([0,5],[2,0])
hold on
plot(5,0,'ro','markersize',3,'markerfacecolor','r')
plot(-5,0,'bo','markersize',3,'markerfacecolor','b')
xlim([-5.1,5.1])
hold off
grid on

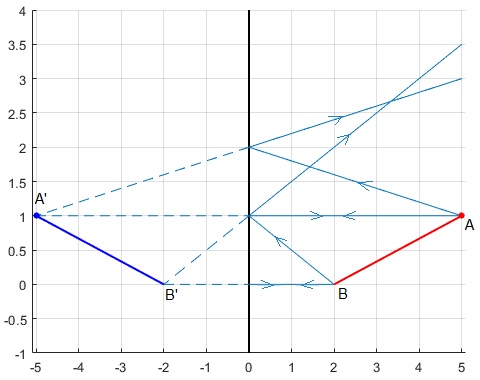
En el caso de que el objeto AB sea extenso. Determinamos las posiciones de las imágenes virtuales de los objetos puntuales A y B

line([0,0],[-1,4], 'LineWidth', 1.5, 'color','k')
line([2,5],[0,1],'lineWidth',1.5,'color','r')
line([-2,-5],[0,1],'lineWidth',1.5,'color','b')
line([-2,0],[0,0],'lineStyle','--')
line([2,0],[0,0])
line([-5,0],[1,1],'lineStyle','--')
line([5,0],[1,1])
line([2,0],[0,1])
line([0,5],[1,3.5])
line([0,-2],[1,0],'lineStyle','--')
line([5,0],[1,2])
line([0,5],[2,3])
line([0,-5],[2,1],'lineStyle','--')

hold on
plot(5,1,'ro','markersize',4,'markerfacecolor','r')
plot(-5,1,'bo','markersize',4,'markerfacecolor','b')
xlim([-5.1,5.1])
hold off
grid on

Dos espejos planos paralelos

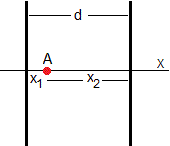
Consideremos dos espejos planos. El primero, contenido en el plano YZ, x=0 y el segundo, paralelo al primero, situado a una distancia x=d

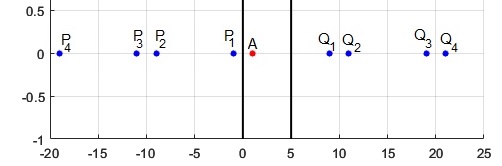
Un objeto puntual A se sitúa entre los dos planos a una distancia x₁ del primero y a una distancia x₂=d-x₁ del segundo

Aplicamos la ley de la reflexión para determinar la posición de las infinitas imágenes virtuales de dicho objeto, situadas a lo largo del eje X

hold on
line([0,0],[-1,3], 'LineWidth', 1.5, 'color','k')
line([5,5],[-1,3], 'LineWidth', 1.5, 'color','k')
plot(1,0,'ro','markersize',4,'markerfacecolor','r')
plot(-1,0,'bo','markersize',4,'markerfacecolor','b')
line([1,0],[0,0.5])
line([0,5],[0.5,3])
line([0,-1],[0.5,0],'lineStyle','--')
line([1,0],[0,0])
line([-1,0],[0,0],'lineStyle','--')

 plot(9,0,'bo','markersize',4,'markerfacecolor','b')
 line([1,5],[0,1])
 line([5,0],[1,9/4])
 line([5,9],[1,0],'lineStyle','--')
 line([1,5],[0,0])
 line([5,9],[0,0],'lineStyle','--')

  plot(11,0,'bo','markersize',4,'markerfacecolor','b')
  line([-1,5],[0,1.5])
  line([5,0],[1.5,1.5+7.5/6])
  line([5,11],[1.5,0],'lineStyle','--')
  line([9,11],[0,0],'lineStyle','--')

  plot(-9,0,'bo','markersize',4,'markerfacecolor','b')
  line([9,0],[0,1])
  line([0,5],[1,1+5/9])
  line([0,-9],[1,0],'lineStyle','--')

  hold off
 grid on

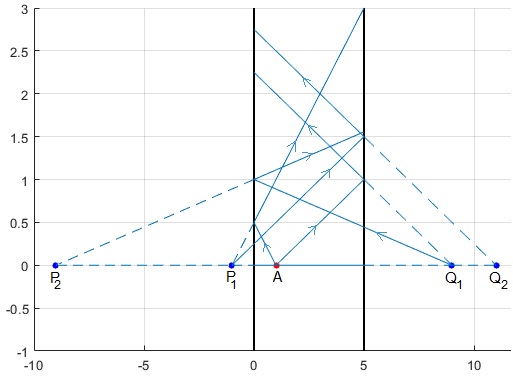
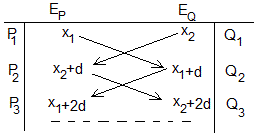
P₁ es la imagen de A producida por el espejo izquierdo, dista x₁ de dicho espejo
Q₁ es la imagen de A producida por el espejo derecho, dista x₂ de dicho espejo
Q₂ es la imagen de P₁ producida por el espejo derecho, dista x₁+d de dicho espejo
P₂ es la imagen de Q₁ producida por el espejo izquierdo, dista x₂+d de dicho espejo
Q₃ es la imagen de P₂ producida por el espejo derecho, que dista x₂+2d de dicho espejo
P₃ es la imagen de Q₂ producida por el espejo izquierdo, que dista x₁+2d de dicho espejo

El código que representa solamente las imágenes virtuales P_k y Q_k del objeto puntual A situado entre los dos espejos paralelos, es

hold on
d=5; %separación
x1=1; %posición objeto
x2=d-x1;
line([0,0],[-1,3], 'LineWidth', 1.5, 'color','k')
line([d,d],[-1,3], 'LineWidth', 1.5, 'color','k')
plot(x1,0,'ro','markersize',4,'markerfacecolor','r')

%imágnes P
for k=0:2:3
    xP=x1+k*d;
    plot(-xP,0,'bo','markersize',4,'markerfacecolor','b')
    xP=x2+(k+1)*d;
    plot(-xP,0,'bo','markersize',4,'markerfacecolor','b')
end
%imágnes Q
for k=0:2:3
    xQ=x2+k*d;
    plot(xQ+d,0,'bo','markersize',4,'markerfacecolor','b')
    xQ=x1+(k+1)*d;
    plot(xQ+d,0,'bo','markersize',4,'markerfacecolor','b')
end
hold off
grid on

Dos espejos planos y perpendiculares

Vamos a determinar las imágenes virtuales de un objeto puntual A situado en la posición (x, y), producidas por dos espejos planos en ángulo recto

hold on
line([0,5],[0,0], 'LineWidth', 1.5, 'color','k')
line([0,0],[0,5], 'LineWidth', 1.5, 'color','k')
line([0,-5],[0,0], 'lineStyle','--','LineWidth', 1.5, 'color','k')
line([0,0],[0,-5], 'lineStyle','--','LineWidth', 1.5, 'color','k')
plot(3,2,'ro','markersize',4,'markerfacecolor','r')
plot(3,-2,'bo','markersize',4,'markerfacecolor','b')
line([3,3],[0,2])
line([3,3],[0,-2],'lineStyle','--')
line([3,1],[2,0])
line([1,0],[0,1])
line([0,4],[1,5])
line([1,3],[0,-2],'lineStyle','--')
plot(-3,2,'bo','markersize',4,'markerfacecolor','b')
line([3,0],[2,2])
line([-3,0],[2,2],'lineStyle','--')
 line([3,0],[2,0.5])
line([-3,0],[2,0.5],'lineStyle','--')
line([0,1],[0.5,0])
line([1,4],[0,1.5])

plot(-3,-2,'bo','markersize',4,'markerfacecolor','b')
line([0,-3],[1,-2],'lineStyle','--')
line([1,-3],[0,-2],'lineStyle','--')
xlim([-3.2,4])
ylim([-2.2,4])
hold off
grid on

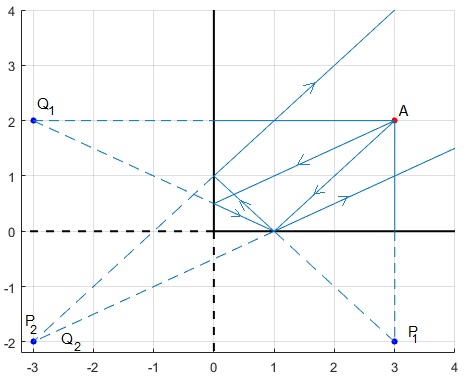
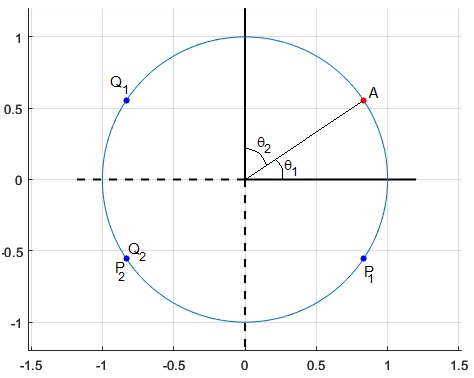
P₁ es la imagen de A producida por el espejo horizontal, dista y de dicho espejo
Q₁ es la imagen de A producida por el espejo vertical, dista x de dicho espejo
Q₂ es la imagen de Q₁ producida por el espejo horizontal
P₂ es la imagen de P₁ producida por el espejo vertical

Q₂ y P₂ coinciden. Este punto es la intersección de la prolongación de los rayos provenientes del objeto A y reflejados por segunda vez en los espejos

Dos espejos planos forman un ángulo θ

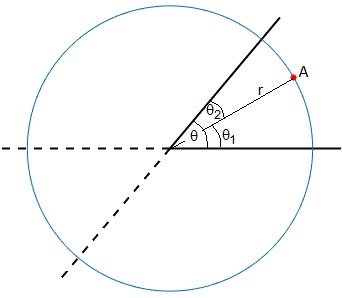
Consideremos el caso de dos espejos planos que forman un ángulo θ. Un objeto puntual A distante r=1 del eje, está situado en una posición que forma un ángulo θ₁ con el espejo horizontal y un ángulo θ₂=θ-θ₁ con el espejo inclinado.

Todas las imágenes virtuales estarán situadas en una circunferencia de radio r=1

Ejemplo

Sea θ=50°, θ₁=30° y θ₂=20°

hold on
th=50*pi/180;
th_1=pi/6;
th_2=th-th_1;
line([0,1.2],[0,0], 'LineWidth', 1.5, 'color','k')
line([0,-1.2],[0,0], 'lineStyle','--','LineWidth', 1.5, 'color','k')
line([0,1.2*cos(th)],[0,1.2*sin(th)], 'LineWidth', 1.5, 'color','k')
line([0,-1.2*cos(th)],[0,-1.2*sin(th)], 'lineStyle','--',
'LineWidth', 1.5, 'color','k')
fplot(@(t) cos(t), @(t) sin(t),[0,2*pi])
plot(cos(th_1),sin(th_1),'ro','markersize',4,'markerfacecolor','r')
%Q
for k=0:2:10
    ang=th_2+k*th;
    if ang<pi 
%         disp((ang+th)*180/pi)
        plot(cos(ang+th),sin(ang+th),'bo','markersize',4,'markerfacecolor','b')
    else
        break;
    end
    ang=th_1+(k+1)*th;
    if ang<pi 
%         disp((ang+th)*180/pi)
        plot(cos(ang+th),sin(ang+th),'bo','markersize',4,'markerfacecolor','b')
    else
        break;
    end
end
%P
for k=0:2:10
    ang=-th_1-k*th;
    if ang>=-pi 
%        disp(ang*180/pi)
        plot(cos(ang),sin(ang),'bo','markersize',4,'markerfacecolor','b')
    else
        break;
    end
    ang=-th_2-(k+1)*th;
     if ang>=-pi 
%        disp(ang*180/pi)
        plot(cos(ang),sin(ang),'bo','markersize',4,'markerfacecolor','b')
     else
         break;
    end
end

ylim([-1.2,1.2])
xlim([-1.2,1.2])
axis equal
hold off
grid on

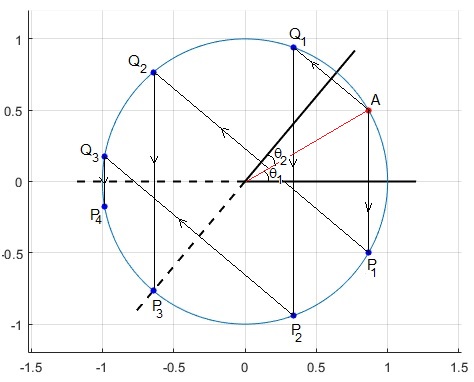
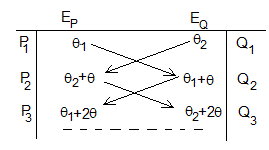
Suprimiendo el símbolo % (comentario) delante de disp(...) se muestran las posiciones angulares de los puntos P_k y Q_k en grados en la ventana de comandos

P₁ es la imagen de A producida por el espejo horizontal, dista θ₁ de dicho espejo
Q₁ es la imagen de A producida por el espejo inclinado, dista θ₂ de dicho espejo
Q₂ es la imagen de P₁ producida por el espejo inclinado, dista θ₁+θ de dicho espejo
P₂ es la imagen de Q₁ producida por el espejo horizontal, que dista θ₂+θ de dicho espejo
Q₃ es la imagen de P₂ producida por el espejo inclinado, dista θ₂+2θ de dicho espejo
P₃ es la imagen de Q₂ producida por el espejo horizontal, dista θ₁+2θ de dicho espejo

Caso particular, θ=90°

Los dos espejos formando un ángulo recto ya se ha estudiado anteriormente. En el script anterior cambiamos las líneas de código th=pi/2; th_1=atan(2/3);. Reproducimos la posición de las tres imágenes virtuales del objeto puntual A cuyas coordenadas son (3,2)

Ejemplos

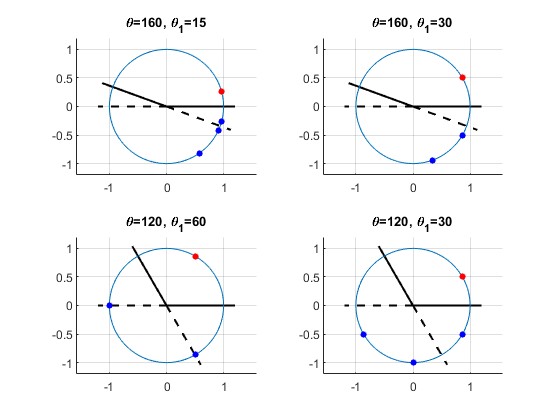
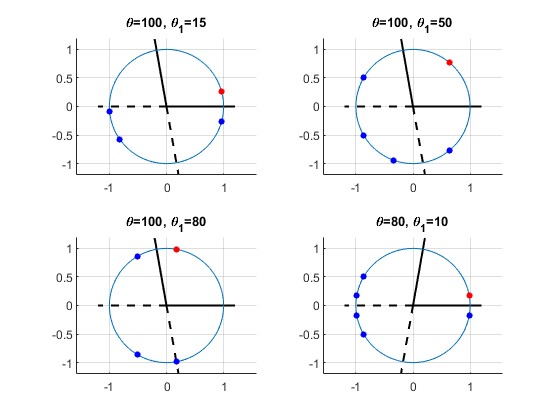
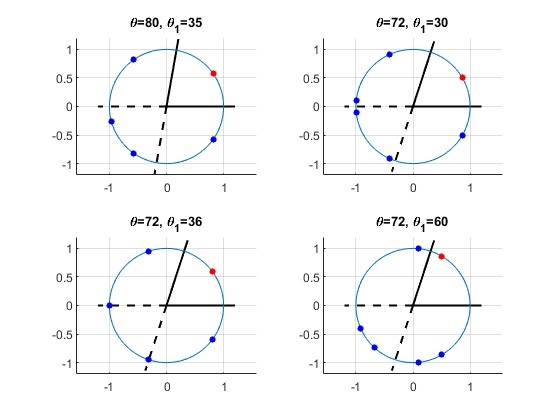
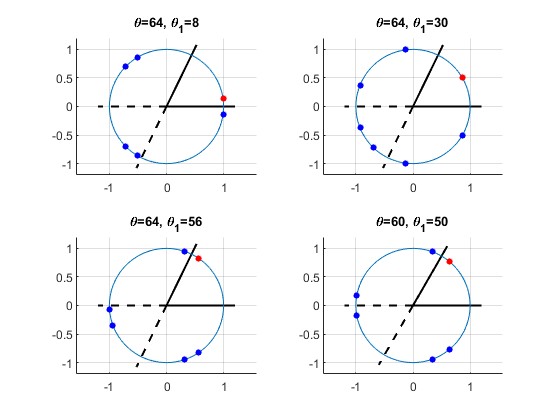
El número total de imágenes virtuales (en color azul) de un objeto puntual A (en color rojo), depende del ángulo θ entre los dos espejos planos y de la posición angular de A (ángulo θ₁) entre dichos espejos

En dos de los artículos que aparecen en las referencias se explica como obtener ese número para distintas situaciones, pero es demasiado prolijo para incluirlo en esta página. A cambio, se muestra una galería de imágenes que el lector puede experimentar cambiando el ángulo de separación θ entre los dos espejos y la posición angular θ₁ del objeto puntual A entre dichos espejos

function reflexion_10     
    subplot(2,2,1)
    imagenes(64*pi/180, 8*pi/180)
    title('\theta=64, \theta_1=8')

    subplot(2,2,2)
    imagenes(64*pi/180, 30*pi/180)
    title('\theta=64, \theta_1=30')

    subplot(2,2,3)
    imagenes(64*pi/180, 56*pi/180)
    title('\theta=64, \theta_1=56')

    subplot(2,2,4)
    imagenes(60*pi/180, 50*pi/180)
    title('\theta=60, \theta_1=50')

    function imagenes(th, th_1)
        hold on
        th_2=th-th_1;
        line([0,1.2],[0,0], 'LineWidth', 1.5, 'color','k')
        line([0,-1.2],[0,0], 'lineStyle','--','LineWidth', 1.5, 'color','k')
        line([0,1.2*cos(th)],[0,1.2*sin(th)], 'LineWidth', 1.5, 'color','k')
        line([0,-1.2*cos(th)],[0,-1.2*sin(th)], 'lineStyle','--',
'LineWidth', 1.5, 'color','k')
        fplot(@(t) cos(t), @(t) sin(t),[0,2*pi])
        plot(cos(th_1),sin(th_1),'ro','markersize',4,
'markerfacecolor','r')
        %Q
        for k=0:2:10
            ang=th_2+k*th;
            if ang<pi 
        %         disp((ang+th)*180/pi)
                plot(cos(ang+th),sin(ang+th),'bo','markersize',4,
'markerfacecolor','b')
            else
                break;
            end
            ang=th_1+(k+1)*th;
            if ang<pi 
        %         disp((ang+th)*180/pi)
                plot(cos(ang+th),sin(ang+th),'bo','markersize',
4,'markerfacecolor','b')
            else
                break;
            end
        end
        %P
        for k=0:2:10
            ang=-th_1-k*th;
            if ang>=-pi 
        %        disp(ang*180/pi)
                plot(cos(ang),sin(ang),'bo','markersize',4,
'markerfacecolor','b')
            else
                break;
            end
            ang=-th_2-(k+1)*th;
             if ang>=-pi 
        %        disp(ang*180/pi)
                plot(cos(ang),sin(ang),'bo','markersize',4,
'markerfacecolor','b')
             else
                 break;
            end
        end  
        ylim([-1.2,1.2])
        xlim([-1.2,1.2])
        axis equal
        hold off
        grid on
    end
end

En cada una de las 16 figuras, el lector puede contar el número de imágenes virtuales del objeto A (punto de color rojo), representadas por puntos de color azul