Recipiente en forma de paralepípedo recto

Sea un líquido de índice de refracción desconocido n_l contenido en una cubeta de vidrio o plástico transparente de índice de refracción n_v. El índice de refracción del aire es n_a=1.

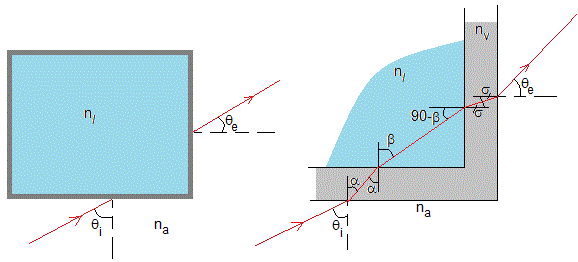
Un rayo de luz LASER incide sobre una de las caras con ángulo θ_i y sale por la otra cara formando un ángulo θ_e con la normal. Aplicamos la ley de Snell de la refracción (véase la parte derecha de la figura)

${\displaystyle \begin{array}{l}{n}_a\sin {\theta }_i=n_v\sin \alpha \\ n_v\sin \alpha =n_l\sin \beta \\ n_l\sin \left(\frac{\pi }{2}-\beta \right)=n_v\sin \sigma \\ n_v\sin \sigma =n_a\sin {\theta }_e\end{array}}$

Se reduce al sistema de ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}{n}_a\sin {\theta }_i=n_l\sin \beta \\ n_a\sin {\theta }_e=n_l\cos \beta \end{array}\\ n_l^2=n_a^2\left({\sin }^2{\theta }_i+{\sin }^2{\theta }_e\right)\end{array}}$

El índice de refracción del líquido n_l no depende del índice de refracción n_v del recipiente, solamente de los ángulos de incidencia θ_i y refractado θ_e.

La dificultad estriba en la medida precisa de estos dos ángulos. En el primer artículo mencionado en las referencias se describe el dispositivo experimental

Recipiente de forma esférica

Un recipiente de forma esférica de radio R contiene el líquido de índice de refracción n desconocido.

Un haz de luz incide en A paralelamente al eje X a una distancia d=Rsinθ, formando un ángulo θ con la dirección radial. Aplicamos la ley de Snell de la refracción, sinθ=n·sinφ. El ángulo del haz refractado es φ<θ.

El haz refractado incide en B en la superficie esférica de separación y se cumple que n·sinφ=sinθ, el haz que sale del recipiente forma un ángulo θ con la dirección radial. Corta al eje X en un punto cuya abscisa f es la distancia focal. La desviación de este haz (ángulo δ que forma con la horizontal) es δ=2(θ-φ)

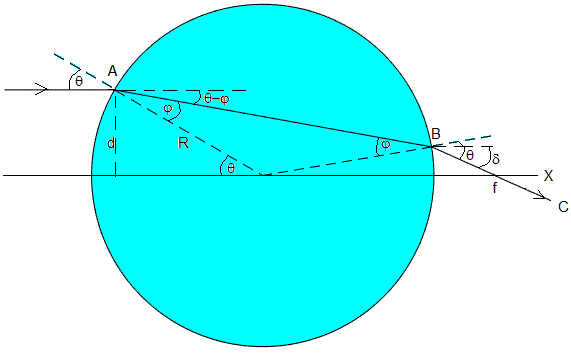
El código para dibujar una parte de la figura es

R=1; %radio
n=1.5; %índice de refracción
hold on
x=(0:360)*pi/180;
fill(R*cos(x),R*sin(x),'c')
plot(R*cos(x),R*sin(x), 'k')
th=pi/6; %ángulo incidente
line([-R-0.1,-R*cos(th)],[R*sin(th),R*sin(th)],'color','k')
phi=asin(sin(th)/n); %refractado
x2=R*cos(th-2*phi);
y2=R*sin(2*phi-th);
line([-R*cos(th),x2],[R*sin(th),y2],'color','k')
f=R*cos(th-2*phi)+R*sin(2*phi-th)/tan(2*(th-phi));
line([x2,f],[y2,0], 'color','k')
line([-R*cos(th),0],[R*sin(th),0],'lineStyle','--', 'color','k')
line([x2,0],[y2,0],'lineStyle','--', 'color','k')
line([-R,R],[0,0],'color','k')
hold off
axis equal
axis off
grid on

• Tramo AB

La ecuación de la recta AB de pendiente -tan(θ-φ) es y=-tan(θ-φ)x+b. La ordenada en el origen b se calcula sabiendo que la recta pasa por A(-Rcosθ, Rsinθ)

${\displaystyle \begin{array}{l}R\sin \theta =-\tan \left(\theta -\phi \right)\left(-R\cos \theta \right)+b\\ b=R\frac{\sin \phi }{\cos \left(\theta -\phi \right)}\end{array}}$

La ecuación de la recta AB es

${\displaystyle y=-\tan \left(\theta -\phi \right)x+R\frac{\sin \phi }{\cos \left(\theta -\phi \right)}}$

El punto B es la intersección de la recta con la circunferencia x²+y²=R²

${\displaystyle \begin{array}{l}{x}^2+{\left(-\tan \left(\theta -\phi \right)x+R\frac{\sin \phi }{\cos \left(\theta -\phi \right)}\right)}^2=R^2\\ \frac{x^2}{{\cos }^2\left(\theta -\phi \right)}-2R\tan \left(\theta -\phi \right)\frac{\sin \phi }{\cos \left(\theta -\phi \right)}x+R^2\frac{{\sin }^2\phi }{{\cos }^2\left(\theta -\phi \right)}-R^2=0\end{array}}$

Las raíces de la ecuación de segundo grado son

${\displaystyle \begin{array}{l}{x}_{\mathrm{1,2}}=\frac{2R\tan \left(\theta -\phi \right)\frac{\sin \phi }{\cos \left(\theta -\phi \right)}\pm \sqrt{4R^2{\tan }^2\left(\theta -\phi \right)\frac{{\sin }^2\phi }{{\cos }^2\left(\theta -\phi \right)}-\frac{4}{{\cos }^2\left(\theta -\phi \right)}\left(R^2\frac{{\sin }^2\phi }{{\cos }^2\left(\theta -\phi \right)}-R^2\right)}}{\frac{2}{{\cos }^2\left(\theta -\phi \right)}}\\ x_{\mathrm{1,2}}=R{\cos }^2\left(\theta -\phi \right)\left(\frac{\sin \phi \sin \left(\theta -\phi \right)}{{\cos }^2\left(\theta -\phi \right)}\pm \frac{\cos \phi }{\cos \left(\theta -\phi \right)}\right)\\ =R\left(\sin \phi \sin \left(\theta -\phi \right)\pm \cos \phi \cos \left(\theta -\phi \right)\right)\end{array}}$

x₁ es el dato de la abscisa del punto A y x₂ es la abscisa del punto B.

${\displaystyle \{\begin{array}{l}{x}_1=-R\cos \left(\theta -\phi +\phi \right)=-R\cos \theta \\ x_2=R\cos \left(\theta -\phi -\phi \right)=R\cos \left(2\phi -\theta \right)\end{array}}$

Introduciendo x₂ en la ecuación de la recta que pasa por A y B, calculamos la ordenada y₂ del punto B

${\displaystyle \begin{array}{l}{y}_2=-\tan \left(\theta -\phi \right)x_2+R\frac{\sin \phi }{\cos \left(\theta -\phi \right)}=\\ y_2=-\frac{\sin \left(\theta -\phi \right)}{\cos \left(\theta -\phi \right)}R\left(\sin \phi \sin \left(\theta -\phi \right)+\cos \phi \cos \left(\theta -\phi \right)\right)+R\frac{\sin \phi }{\cos \left(\theta -\phi \right)}\\ y_2=R\left(\sin \phi \cos \left(\theta -\phi \right)-\cos \phi \sin \left(\theta -\phi \right)\right)=R\sin \left(2\phi -\theta \right)\end{array}}$

• Tramo BC

La ecuación de la recta BC es y=-tanδ·x+b', con δ=2(θ-φ). La ordenada en el origen b' se calcula sabiendo que la recta pasa por B(x₂, y₂)

${\displaystyle \begin{array}{l}{y}_2=-\tan \delta ·x_2+b\text{'}\\ b\text{'}=y_2+\tan \delta ·x_2\end{array}}$

La posición del foco F es la intersección f de esta recta con el eje X. Poniendo y=0 en la ecuación de la recta BC

${\displaystyle f=\frac{b\text{'}}{\tan \delta }=x_2+\frac{y_2}{\tan \delta }=R\cos \left(2\phi -\theta \right)+\frac{R\sin \left(2\phi -\theta \right)}{\tan \left(2\left(\theta -\phi \right)\right)}=R\frac{\sin \theta }{\sin \left(2\left(\theta -\phi \right)\right)}}$

Aproximación paraxial

Cuando el ángulo α es pequeño, sinα≈α.

La ley de la refracción, sinθ=n·sinφ, se aproxima a θ≈n·φ

${\displaystyle f\approx R\frac{\theta }{2\left(\theta -\phi \right)}=R\frac{\theta }{2\left(\theta -\frac{\theta }{n}\right)}=R\frac{n}{2(n-1)}}$

Supongamos un recipiente esférico de radio R=3.08 cm que contiene agua cuyo índice de refracción n=1.3304 para la luz de color rojo (λ=635 nm). Trazamos los rayos de luz que distan d=iR/10, i=1,2,3...9 del eje X. Representamos mediante un punto la posición del foco f en la aproximación paraxial

R=3.08; %radio
n=1.3304; %índice de refracción del agua
hold on
x=(0:360)*pi/180;
fill(R*cos(x),R*sin(x),'c')
plot(R*cos(x),R*sin(x), 'k')
for i=1:9
    th=asin(i/10);
    line([-R-1,-R*cos(th)],[R*sin(th),R*sin(th)],'color','r')
    line([-R-1,-R*cos(th)],[-R*sin(th),-R*sin(th)],'color','r')
    phi=asin(sin(th)/n); %refractado
    x2=R*cos(th-2*phi);
    y2=R*sin(2*phi-th);
    line([-R*cos(th),x2],[R*sin(th),y2],'color','r')
    line([-R*cos(th),x2],[-R*sin(th),-y2],'color','r')
    f=R*sin(th)/sin(2*(th-phi));
    line([x2,f],[y2,0], 'color','r')
    line([x2,f],[-y2,0], 'color','r')
end
plot(R*n/(2*(n-1)),0, 'o','markersize',3,'markeredgecolor','b',
'markerfacecolor','b')
line([-R-1,2.1*R],[0,0],'color','k')
hold off
axis equal
axis off
grid on

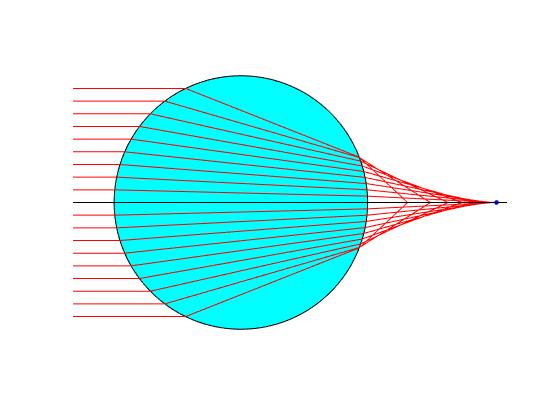
Cálculo del índice de refracción

Un haz de luz LASER de color rojo (λ=635 nm) se divide en dos haces paralelos al eje X equidistantes que inciden sobre la superficie esférica de un recipiente de radio R=3.08 cm que contiene agua, cuyo índice de refracción n vamos a determinar

Se mide la posición del foco, la abscisa de la intersección de los haces paralelos con el eje X, f=6.18 cm

• Aproximación paraxial

Dado f y R despejamos n

${\displaystyle n=\frac{2f}{2f-R}}$

El resultado es n=1.3319

• Resolviendo una ecuación transcendente

Dada la distancia d=Rsinθ del haz de luz al eje X o el ángulo θ, la posición del foco f y el radio del recipiente, R, resolvemos la ecuación transcendente

${\displaystyle \frac{f}{R}=\frac{\sin \theta }{\sin \left(2\left(\theta -\phi \right)\right)}}$

• Representamos la función y determinamos su intersección con el eje X (el ángulo φ)

R=3.08; %radio
f=6.18; %posición del foco
th=10*pi/180; %ángulo incidente
g=@(x) sin(th)./sin(2*(th-x))-f/R;
fplot(g,[0,th])
ylim([-3,3])
grid on
xlabel('\phi')
ylabel('f(\phi)')
title('Angulo refractado, \phi')



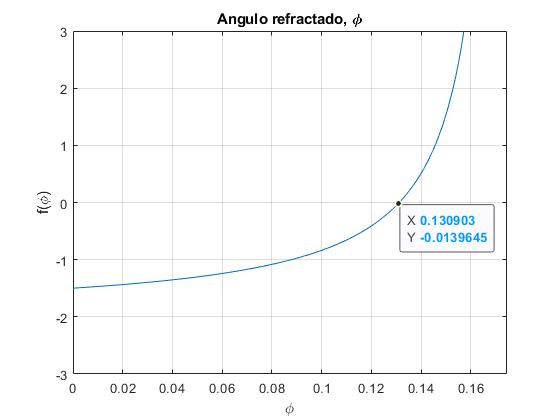
El ángulo del rayo incidente es θ=10°, el ángulo del rayo refractado φ=0.1309 (7.5°). Por tanto, el índice de refracción n es

${\displaystyle n=\frac{\sin \theta }{\sin \phi }}$

El resultado es n=1.3304

• Utilizamos la función fzero de MATLAB para resolver la ecuación transcendente, calculando el ángulo φ

>> phi=fzero(g,th/2)
phi =    0.1312
>> n=sin(th)/sin(phi)
n =    1.3273

El resultado es n=1.3273

Representamos el recipiente y los dos haces de luz roja, inicialmente paralelos, hasta que llegan al foco F

R=3.08; %radio
n=1.3304; %índice de refracción del agua

hold on
x=(0:360)*pi/180;
fill(R*cos(x),R*sin(x),'c')
plot(R*cos(x),R*sin(x), 'k')
th=10*pi/180; %ángulo incidente
line([-R-1,-R*cos(th)],[R*sin(th),R*sin(th)],'color','r')
line([-R-1,-R*cos(th)],[-R*sin(th),-R*sin(th)],'color','r')
phi=asin(sin(th)/n); %refractado
x2=R*cos(th-2*phi);
y2=R*sin(2*phi-th);
line([-R*cos(th),x2],[R*sin(th),y2],'color','r')
line([-R*cos(th),x2],[-R*sin(th),-y2],'color','r')
f=R*sin(th)/sin(2*(th-phi));
line([x2,f],[y2,0], 'color','r')
line([x2,f],[-y2,0], 'color','r')
plot(f,0, 'o','markersize',3,'markeredgecolor','r','markerfacecolor','r')
line([-R,2.5*R],[0,0],'color','k')
line([-R*cos(th),0],[R*sin(th),0],'lineStyle','--', 'color','k')
hold off
axis equal
grid on

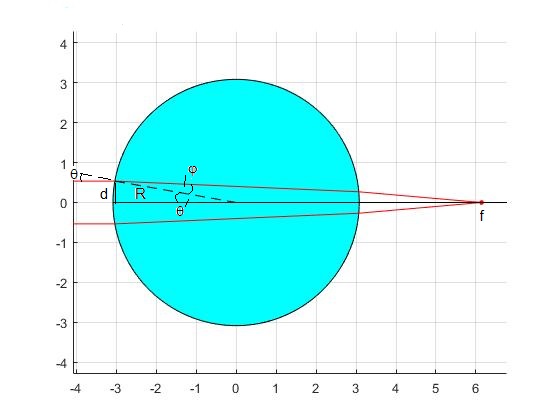
Se sugiere al lector calcular los índices de refracción del etanol y de un aceite vegetal contenidos en un recipiente esférico de radio R=3.08 cm. Las medidas de la distancia focal son f=5.59 cm para el primero y f=4.79 cm para el segundo, respectivamente

Tubo capilar

En esta sección, se describe la medida del índice de refracción n de un líquido contenido en un tubo capilar de radio interior r y exterior R. El índice de refracción del tubo es n₀>n.

Un tubo capilar de radio R=0.5 mm se ilumina con luz de un LASER He-Ne de λ=632.8 nm de longitud de onda. La luz dispersada procede de las reflexiones de la luz con la superficie exterior e interior del capilar, que no tendremos en cuenta. Se tomarán en consideración tres rayos y se medirán sus ángulos de desviación, a partir de estas tres medidas obtendremos:

• el índice de refracción n₀ del tubo
• el cociente r/R entre el radio interior y el radio exterior de dicho tubo
• el índice de refracción n del líquido que contiene el tubo capilar

Rayo 1

El primer rayo ABC es idéntico al estudiado en la sección anterior, cambiando el índice de refracción n por n₀.

Un haz de luz incide en A paralelamente al eje X, formando un ángulo θ con la dirección radial. Aplicamos la ley de Snell de la refracción, sinθ=n₀·sinφ. El ángulo del haz refractado es φ<θ.

El haz refractado incide en B en la superficie esférica de separación y se cumple que n₀·sinφ=sinθ, el haz que sale del recipiente forma un ángulo θ con la dirección radial. El ángulo de desviación δ₁=2(θ-φ)

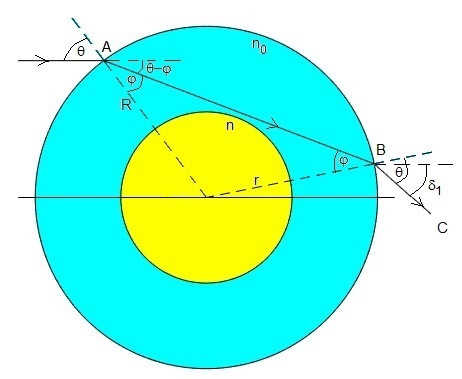
El código para dibujar una parte de la figura es

R=1; %radio exterior
r=0.5; %radio interior
n0=1.5; %índice de refracción del tubo
hold on
x=(0:360)*pi/180;
fill(R*cos(x),R*sin(x),'c')
plot(R*cos(x),R*sin(x), 'k')
fill(r*cos(x),r*sin(x),'y')
plot(r*cos(x),r*sin(x), 'k')

th=asin(0.8/R); %ángulo incidente
line([-R-0.1,-R*cos(th)],[R*sin(th),R*sin(th)],'color','k')
phi=asin(sin(th)/n0); %refractado
x2=R*cos(th-2*phi);
y2=R*sin(2*phi-th);
line([-R*cos(th),x2],[R*sin(th),y2],'color','k')
%transmitido
f=R*sin(th)/sin(2*(th-phi));
line([x2,f],[y2,0], 'color','k')

line([-R*cos(th),0],[R*sin(th),0],'lineStyle','--', 'color','k')
line([x2,0],[y2,0],'lineStyle','--', 'color','k')
line([-1.1*R,1.1*R],[0,0],'color','k')
hold off
axis equal
axis off
grid on

• Tramo AB

La ecuación de la recta AB de pendiente -tan(θ-φ) es y=-tan(θ-φ)x+b. La ordenada en el origen b se calcula sabiendo que la recta pasa por A(-Rcosθ, Rsinθ)

${\displaystyle \begin{array}{l}R\sin \theta =-\tan \left(\theta -\phi \right)\left(-R\cos \theta \right)+b\\ b=R\frac{\sin \phi }{\cos \left(\theta -\phi \right)}\end{array}}$

La ecuación de la recta AB es

${\displaystyle y=-\tan \left(\theta -\phi \right)x+R\frac{\sin \phi }{\cos \left(\theta -\phi \right)}}$

El punto B es la intersección de la recta con la circunferencia x²+y²=R²

${\displaystyle \begin{array}{l}{x}^2+{\left(-\tan \left(\theta -\phi \right)x+R\frac{\sin \phi }{\cos \left(\theta -\phi \right)}\right)}^2=R^2\\ \frac{x^2}{{\cos }^2\left(\theta -\phi \right)}-2R\tan \left(\theta -\phi \right)\frac{\sin \phi }{\cos \left(\theta -\phi \right)}x+R^2\frac{{\sin }^2\phi }{{\cos }^2\left(\theta -\phi \right)}-R^2=0\end{array}}$

Las raíces de la ecuación de segundo grado son

${\displaystyle \begin{array}{l}{x}_{\mathrm{1,2}}=\frac{2R\tan \left(\theta -\phi \right)\frac{\sin \phi }{\cos \left(\theta -\phi \right)}\pm \sqrt{4R^2{\tan }^2\left(\theta -\phi \right)\frac{{\sin }^2\phi }{{\cos }^2\left(\theta -\phi \right)}-\frac{4}{{\cos }^2\left(\theta -\phi \right)}\left(R^2\frac{{\sin }^2\phi }{{\cos }^2\left(\theta -\phi \right)}-R^2\right)}}{\frac{2}{{\cos }^2\left(\theta -\phi \right)}}\\ x_{\mathrm{1,2}}=R{\cos }^2\left(\theta -\phi \right)\left(\frac{\sin \phi \sin \left(\theta -\phi \right)}{{\cos }^2\left(\theta -\phi \right)}\pm \frac{\cos \phi }{\cos \left(\theta -\phi \right)}\right)\\ =R\left(\sin \phi \sin \left(\theta -\phi \right)\pm \cos \phi \cos \left(\theta -\phi \right)\right)\end{array}}$

x₁ es el dato de la abscisa del punto A y x₂ es la abscisa del punto B.

${\displaystyle \{\begin{array}{l}{x}_1=-R\cos \left(\theta -\phi +\phi \right)=-R\cos \theta \\ x_2=R\cos \left(\theta -\phi -\phi \right)=R\cos \left(2\phi -\theta \right)\end{array}}$

Introduciendo x₂ en la ecuación de la recta que pasa por A y B, calculamos la ordenada y₂ del punto B

${\displaystyle \begin{array}{l}{y}_2=-\tan \left(\theta -\phi \right)x_2+R\frac{\sin \phi }{\cos \left(\theta -\phi \right)}=\\ y_2=-\frac{\sin \left(\theta -\phi \right)}{\cos \left(\theta -\phi \right)}R\left(\sin \phi \sin \left(\theta -\phi \right)+\cos \phi \cos \left(\theta -\phi \right)\right)+R\frac{\sin \phi }{\cos \left(\theta -\phi \right)}\\ y_2=R\left(\sin \phi \cos \left(\theta -\phi \right)-\cos \phi \sin \left(\theta -\phi \right)\right)=R\sin \left(2\phi -\theta \right)\end{array}}$

• Tramo BC

La ecuación de la recta BC es y=-tanδ₁·x+b', con δ₁=2(θ-φ). La ordenada en el origen b' se calcula sabiendo que la recta pasa por B(x₂, y₂)

${\displaystyle y=-\tan \left(2\left(\theta -\phi \right)\right)·x+R\frac{\sin \theta }{\cos \left(2\left(\theta -\phi \right)\right)}}$

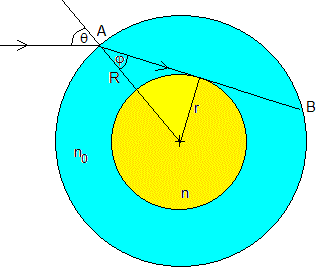
Cuando el ángulo incidente θ disminuye el refractado AB llega un momento en que se hace tangente a la circunferencia de radio r.

El ángulo del rayo refractado, sinφ=r/R

El ángulo del rayo incidente límite es sinθ_l=n₀sinφ

${\displaystyle {\theta }_l=\arcsin \left(n_0\frac{r}{R}\right)}$

El rayo 1 se produce para los ángulos θ de los rayos incidentes paralelos al eje X tales que θ_l<θ<π/2

Angulo de desviación

Representamos el ángulo de desviación δ₁ en función del ángulo incidente θ en el intervalo θ_l<θ<π/2.

${\displaystyle {\delta }_1=2\left(\theta -\phi \right)=2\left(\theta -\arcsin \left(\frac{\sin \theta }{n_0}\right)\right)}$

R=1; %radio exterior
r=0.5; %radio interior
n0=1.5; %índice de refracción
n=1.33; %índice de refración del agua
th_lim=asin(n0*r/R); %límite inferior
f=@(x) 2*(x-asin(sin(x)/n0));
fplot(f,[th_lim,pi/2])
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','15','30','45','60','75','90'})
set(gca,'YTick', 0:pi/12:pi/2)
set(gca,'YTickLabel',{'0','15','30','45','60','75','90'})
grid on
xlabel('\theta')
ylabel('\delta_1')
title('Angulo de desviación, rayo 1')

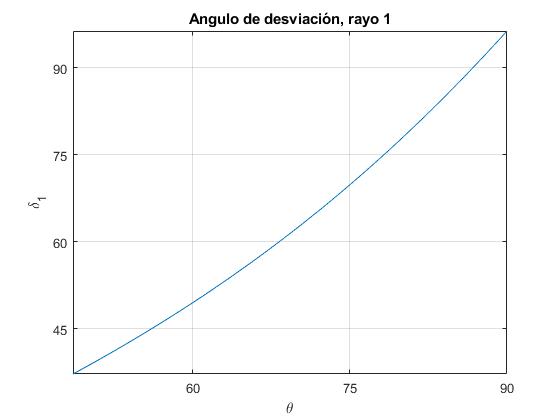
Vemos que es una función creciente, designamos α₁ el valor menor del ángulo de desviación δ₁

${\displaystyle {\alpha }_1=2\left({\theta }_l-\arcsin \left(\frac{\sin {\theta }_l}{n_0}\right)\right)=2\left(\arcsin \left(\frac{n_{0}r}{R}\right)-\arcsin \left(\frac{r}{R}\right)\right)}$

Rayo 2

El rayo iniciente paralelo al eje X se refracta en A y llega a B, en parte se refracta y en parte se refleja. El rayo 1 es el refractado que hemos estudiado y el rayo 2 es el reflejado en B, que se refracta cuando llega a C. Tal como ocurre al estudiar el arco primario del arco iris

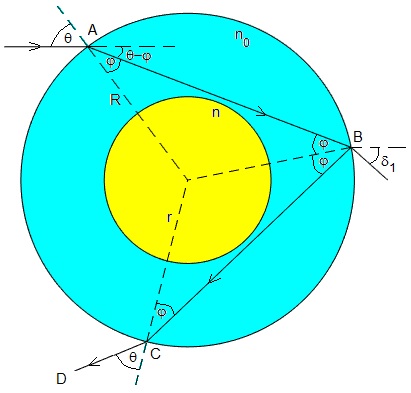
• Tramo BC

Las coordenadas del punto B son

${\displaystyle \{\begin{array}{l}{x}_2=R\cos \left(2\phi -\theta \right)\\ y_2=R\sin \left(2\phi -\theta \right)\end{array}}$

La recta BC hace el ángulo 2φ-(θ-φ)=3φ-θ. La ecuación de la recta que pasa por BC es

${\displaystyle y=\tan \left(3\phi -\theta \right)x+b}$

La ordenada en el origen b se determina sabiendo que la recta pasa por el punto B (x₂,y₂)

${\displaystyle \begin{array}{l}R\sin \left(2\phi -\theta \right)=\tan \left(3\phi -\theta \right)R\cos \left(2\phi -\theta \right)+b\\ b=R\frac{\sin \left(2\phi -\theta \right)\cos \left(3\phi -\theta \right)-\cos \left(2\phi -\theta \right)\sin \left(3\phi -\theta \right)}{\cos \left(3\phi -\theta \right)}=R\frac{\sin \left(2\phi -\theta -\left(3\phi -\theta \right)\right)}{\cos \left(3\phi -\theta \right)}=-R\frac{\sin \phi }{\cos \left(3\phi -\theta \right)}\end{array}}$

La ecuación de la recta BC es

${\displaystyle y=\tan \left(3\phi -\theta \right)x-R\frac{\sin \phi }{\cos \left(3\phi -\theta \right)}}$

El punto C está en la intersección de esta recta y la circunferencia x²+y²=R²

${\displaystyle \begin{array}{l}\frac{x^2}{{\cos }^2\left(3\phi -\theta \right)}-2R\tan \left(3\phi -\theta \right)\frac{\sin \phi }{\cos \left(3\phi -\theta \right)}x+R^2\frac{{\sin }^2\phi }{{\cos }^2\left(3\phi -\theta \right)}-R^2=0\\ x_{\mathrm{2,3}}=\frac{2R\tan \left(3\phi -\theta \right)\frac{\sin \phi }{\cos \left(3\phi -\theta \right)}\pm \sqrt{4R^2{\tan }^2\left(3\phi -\theta \right)\frac{{\sin }^2\phi }{{\cos }^2\left(3\phi -\theta \right)}-4R^2\left(\frac{{\sin }^2\phi }{{\cos }^2\left(3\phi -\theta \right)}-1\right)\frac{1}{{\cos }^2\left(3\phi -\theta \right)}}}{\frac{2}{{\cos }^2\left(3\phi -\theta \right)}}=\\ R\sin \left(3\phi -\theta \right)\sin \phi \pm R\sqrt{-\frac{{\sin }^2\phi }{{\cos }^2\left(3\phi -\theta \right)}+\frac{1}{{\cos }^2\left(3\phi -\theta \right)}}{\cos }^2\left(3\phi -\theta \right)\\ =R\sin \left(3\phi -\theta \right)\sin \phi \pm R\cos \left(3\phi -\theta \right)\cos \phi \end{array}}$

Obtenemos las abscisas del punto B, x₂ y la del punto C, x₃

${\displaystyle \{\begin{array}{l}{x}_2=R\cos \left(2\phi -\theta \right)\\ x_3=-R\cos \left(4\phi -\theta \right)\end{array}}$

Utilizamos la ecuación de la recta BC para calcular la ordenada y₃ del punto C

${\displaystyle \begin{array}{l}{y}_3=-\tan \left(3\phi -\theta \right)R\cos \left(4\phi -\theta \right)-R\frac{\sin \phi }{\cos \left(3\phi -\theta \right)}=\\ -R\frac{\sin \left(3\phi -\theta \right)\left(\cos \left(3\phi -\theta \right)\cos \phi -\sin \left(3\phi -\theta \right)\sin \phi \right)+\sin \phi }{\cos \left(3\phi -\theta \right)}=\\ -R\left(\sin \left(3\phi -\theta \right)\cos \phi +\cos \left(3\phi -\theta \right)\sin \phi \right)=-R\sin \left(4\phi -\theta \right)\end{array}}$

• Tramo CD

La desviación del rayo refractado CD es δ₂=π-(3φ-θ-(θ-φ))=π+2θ-4φ. La recta CD forma un ángulo 4φ-2θ con el eje horizontal. La ecuación de la recta es

${\displaystyle y=\tan \left(4\phi -2\theta \right)x+b}$

La ordenda en el origen b se calcula, sabiendo que la recta pasa por el punto C(x₃,y₃)

${\displaystyle \begin{array}{l}-R\sin \left(4\phi -\theta \right)=-\tan \left(4\phi -2\theta \right)R\cos \left(4\phi -\theta \right)+b\\ b=R\frac{\sin \left(4\phi -2\theta \right)\cos \left(4\phi -\theta \right)-\cos \left(4\phi -2\theta \right)\sin \left(4\phi -\theta \right)}{\cos \left(4\phi -2\theta \right)}=-R\frac{\sin \theta }{\cos \left(4\phi -2\theta \right)}\end{array}}$

La ecuación de la recta CD es

${\displaystyle y=\tan \left(4\phi -2\theta \right)x-R\frac{\sin \theta }{\cos \left(4\phi -2\theta \right)}}$

Angulo de desviación

Se muestra el camino que siguen 9 rayos inicialmente paralelos al eje X, equidistantes en el intervalo θ_l<θ<π/2

R=1; %radio exterior
r=0.5; %radio interior
n0=1.5; %índice de refracción
n=1.33; %índice de refración del agua
hold on
x=(0:360)*pi/180;
fill(R*cos(x),R*sin(x),'c')
plot(R*cos(x),R*sin(x), 'k')
fill(r*cos(x),r*sin(x),'y')
plot(r*cos(x),r*sin(x), 'k')
th_lim=asin(n0*r/R);
d_lim=R*sin(th_lim);
for i=1:9
    d=d_lim+(R-d_lim)*i/10;
    th=asin(d/R);
    line([-R-0.1,-R*cos(th)],[R*sin(th),R*sin(th)],'color','k')
    phi=asin(sin(th)/n0); %refractado
    x2=R*cos(th-2*phi);
    y2=R*sin(2*phi-th);
    line([-R*cos(th),x2],[R*sin(th),y2],'color','k')
    f=R*(sin(th)+sin(2*(th-phi))/2)/sin(2*(th-phi));
    line([x2,f],[y2,-R/2], 'color','k')
%rayo reflejado
    x3=-R*cos(4*phi-th);
    y3=-R*sin(4*phi-th);
    line([x2,x3],[y2,y3],'color','k')
    x4=-R*cos(4*phi-th)-0.3;
    y4=tan(4*phi-2*th)*x4-R*sin(th)/cos(4*phi-2*th);
    line([x3,x4],[y3, y4],'color','k')
end
hold off
axis equal
axis off
grid on

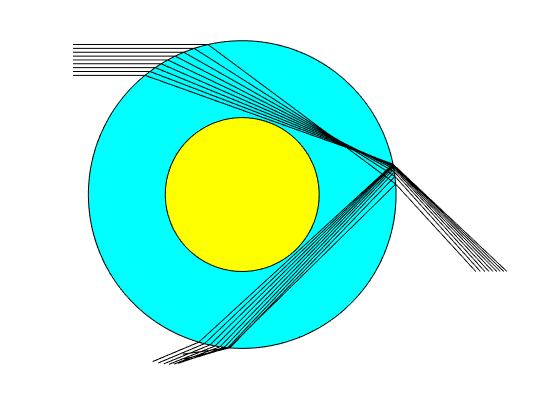
Representamos el ángulo de desviación δ₂ en función del ángulo incidente θ en el intervalo θ_l<θ<π/2.

${\displaystyle {\delta }_2=\pi +2\theta -4\arcsin \left(\frac{\sin \theta }{n_0}\right)}$

R=1; %radio exterior
r=0.5; %radio interior
n0=1.5; %índice de refracción
n=1.33; %índice de refración del agua
th_lim=asin(n0*r/R);
f=@(x) 2*x-4*asin(sin(x)/n0)+pi;
fplot(f,[th_lim,pi/2])
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','15','30','45','60','75','90'})
set(gca,'YTick', pi/2:pi/12:pi)
set(gca,'YTickLabel',{'90','105','120','135','150','165','180'})
grid on
ylim([f(th_lim)-0.1, f(pi/2)])
xlabel('\theta')
ylabel('\delta_2')
title('Angulo de desviación, rayo 2')

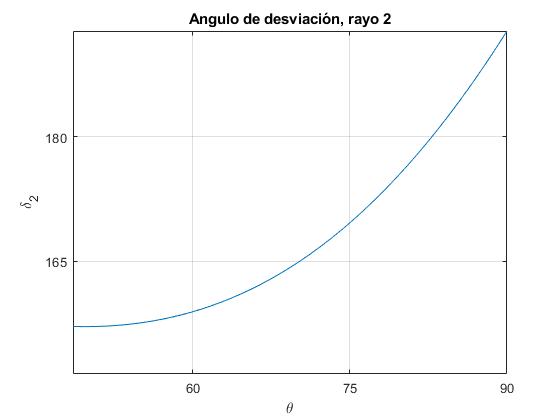
La función que tiene un mínimo

${\displaystyle \begin{array}{l}\frac{d{\delta }_2}{d\theta }=2-4\frac{\frac{\cos \theta }{n_0}}{\sqrt{1-\frac{{\sin }^2\theta }{n_0^2}}}=0\\ \frac{4{\cos }^2\theta +{\sin }^2\theta }{n_0^2}=1\\ 4-3{\sin }^2\theta =n_0^2\\ \sin \theta =\sqrt{\frac{4-n_0^2}{3}}\end{array}}$

Designamos por α₂ el ángulo de desviación, para este ángulo de incidencia

${\displaystyle {\alpha }_2=\pi +2\arcsin \left(\sqrt{\frac{4-n_0^2}{3}}\right)-4\arcsin \left(\frac{1}{n_0}\sqrt{\frac{4-n_0^2}{3}}\right)}$

La medida del ángulo α₂ nos proporciona el índice de refracción del tubo n₀. Conocido n₀, la medida del ángulo α₁ nos proporciona el cociente r/R entre los radios interior r y exterior R del tubo.

Rayo 3

El rayo 3 atraviesa el líquido contenido en el capilar

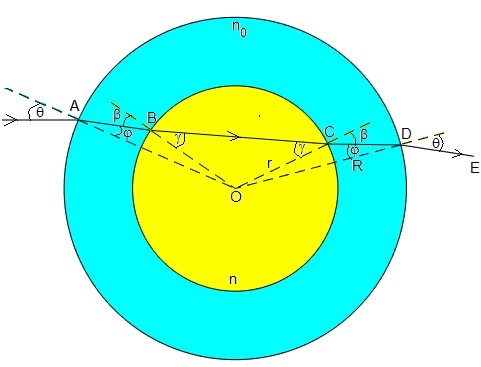
• Tramo AB

Un rayo de luz incide en A paralelamente al eje X, formando un ángulo θ con la dirección radial. Aplicamos la ley de Snell de la refracción, sinθ=n₀·sinφ. El ángulo refractado es φ<θ.

La ecuación de la recta AB de pendiente -tan(θ-φ) es y=-tan(θ-φ)x+b. La ordenada en el origen b se calcula sabiendo que la recta pasa por A(-Rcosθ, Rsinθ)

${\displaystyle \begin{array}{l}R\sin \theta =-\tan \left(\theta -\phi \right)\left(-R\cos \theta \right)+b\\ b=R\frac{\sin \phi }{\cos \left(\theta -\phi \right)}\end{array}}$

La ecuación de la recta AB es

${\displaystyle y=-\tan \left(\theta -\phi \right)x+R\frac{\sin \phi }{\cos \left(\theta -\phi \right)}}$

El punto B es la intersección de la recta con la circunferencia x²+y²=r²

${\displaystyle \begin{array}{l}{x}^2+{\left(-\tan \left(\theta -\phi \right)x+R\frac{\sin \phi }{\cos \left(\theta -\phi \right)}\right)}^2=r^2\\ \frac{x^2}{{\cos }^2\left(\theta -\phi \right)}-2R\tan \left(\theta -\phi \right)\frac{\sin \phi }{\cos \left(\theta -\phi \right)}x+R^2\frac{{\sin }^2\phi }{{\cos }^2\left(\theta -\phi \right)}-r^2=0\end{array}}$

La abscisa x₂ de B es la raíz menor de la ecuación de segundo grado

${\displaystyle \begin{array}{l}{x}_2=\frac{2R\tan \left(\theta -\phi \right)\frac{\sin \phi }{\cos \left(\theta -\phi \right)}-\sqrt{4R^2{\tan }^2\left(\theta -\phi \right)\frac{{\sin }^2\phi }{{\cos }^2\left(\theta -\phi \right)}-\frac{4}{{\cos }^2\left(\theta -\phi \right)}\left(R^2\frac{{\sin }^2\phi }{{\cos }^2\left(\theta -\phi \right)}-r^2\right)}}{\frac{2}{{\cos }^2\left(\theta -\phi \right)}}=\\ R\left(\sin \left(\theta -\phi \right)\sin \phi -\cos \left(\theta -\phi \right)\sqrt{\frac{r^2}{R^2}-{\sin }^2\phi }\right)\end{array}}$

Para que exista esta raíz se tiene que cumplir que

${\displaystyle \begin{array}{l}\frac{r}{R}\ge \sin \phi \\ \frac{r}{R}\ge \frac{\sin \theta }{n_0}\\ \theta \le \arcsin \left(\frac{n_{0}r}{R}\right)\end{array}}$

Utilizamos la ecuación de la recta AB para calcular la ordenada y₂ del punto B

${\displaystyle \begin{array}{l}{y}_2=-\tan \left(\theta -\phi \right)x_2+R\frac{\sin \phi }{\cos \left(\theta -\phi \right)}=\\ R\left(\cos \left(\theta -\phi \right)\sin \phi +\sin \left(\theta -\phi \right)\sqrt{\frac{r^2}{R^2}-{\sin }^2\phi }\right)\end{array}}$

• Tramo BC

El rayo refractado incide en B en la superficie esférica de separación y se cumple que n₀·sinβ=n·sinγ.

En el triángulo AOB aplicamos el teorema del seno

${\displaystyle \begin{array}{l}\frac{\sin \phi }{r}=\frac{\sin \left(\pi -\beta \right)}{R}\\ \sin \beta =\frac{R}{r}\sin \phi \end{array}}$

El ángulo de desviación del rayo refractado BC en el líquido es δ=(θ-φ)+(β-γ). La ecuación de la recta, que pasa por el punto B (x₂, y₂), es

${\displaystyle \begin{array}{l}y=-\tan \delta ·x+b\\ \delta =\left(\theta -\phi \right)+\left(\beta -\gamma \right),b=y_2+x_2\tan \delta \end{array}}$

El punto C es la intersección de esta recta con la circunferencia x²+y²=r²

${\displaystyle \begin{array}{l}\frac{x^2}{{\cos }^2\delta }-2b\tan \delta ·x+b^2-r^2=0\\ x_3=\cos \delta \left(b\sin \delta +\sqrt{r^2-b^2{\cos }^2\delta }\right)\\ y_3=-\tan \delta ·x_3+b\end{array}}$

El punto C existe si r≥bcosδ

• Tramo CD

El ángulo de desviación del rayo refractado CD en el tubo es δ=(θ-φ)+2(β-γ). La ecuación de la recta, que pasa por el punto C (x₃, y₃), es

${\displaystyle \begin{array}{l}y=-\tan \delta ·x+b\\ \delta =\left(\theta -\phi \right)+2\left(\beta -\gamma \right),b=y_3+x_3\tan \delta \end{array}}$

El punto D es la intersección de esta recta con la circunferencia x²+y²=R²

${\displaystyle \begin{array}{l}\frac{x^2}{{\cos }^2\delta }-2b\tan \delta ·x+b^2-R^2=0\\ x_4=\cos \delta \left(b\sin \delta +\sqrt{R^2-b^2{\cos }^2\delta }\right)\\ y_4=-\tan \delta ·x_4+b\end{array}}$

El punto D existe si R≥bcosδ

• Tramo DE

El ángulo de desviación del rayo refractado DE es δ=2(θ-φ)+2(β-γ). La ecuación de la recta, que pasa por el punto D (x₄, y₄), es

${\displaystyle \begin{array}{l}y=-\tan \delta ·x+b\\ \delta =2\left(\theta -\phi \right)+2\left(\beta -\gamma \right),b=y_4+x_4\tan \delta \end{array}}$

Angulo de desviación

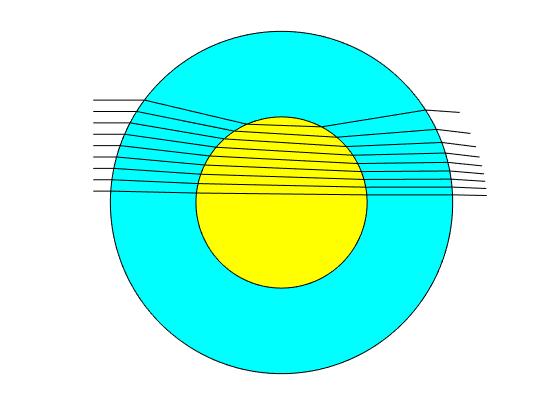
Se muestra el camino que siguen 9 rayos inicialmente paralelos al eje X, equidistantes en el intervalo 0<θ<arcsin(nr/R)

R=1; %radio exterior
r=0.5; %radio interior
n0=1.5; %índice de refracción vidrio
n=1.33; %índice refracción agua
hold on
x=(0:360)*pi/180;
fill(R*cos(x),R*sin(x),'c')
plot(R*cos(x),R*sin(x), 'k')
fill(r*cos(x),r*sin(x),'y')
plot(r*cos(x),r*sin(x), 'k')
th_lim=asin(n*r/R);
d_lim=R*sin(th_lim);
for i=1:9
    d=d_lim*i/10;
    th=asin(d/R);
    line([-R-0.1,-R*cos(th)],[R*sin(th),R*sin(th)],'color','k')
    phi=asin(sin(th)/n0); %refractado
    x2=R*sin(th-phi)*sin(phi)-R*sqrt((r/R)^2-sin(phi)^2)*cos(th-phi);
    y2=-tan(th-phi)*x2+R*sin(phi)/cos(th-phi);
    line([-R*cos(th),x2],[R*sin(th),y2],'color','k')
    alfa=asin(R*sin(phi)/r);
    beta=asin(n0*sin(alfa)/n);
    delta=th-phi+alfa-beta;
    b=y2+tan(delta)*x2;
    x3=cos(delta)*(b*sin(delta)+sqrt(r^2-(b*cos(delta))^2));
    y3=-tan(delta)*x3+b;
    line([x3,x2],[y3,y2],'color','k')
    delta=th-phi+2*(alfa-beta);
    b=y3+tan(delta)*x3;
    x4=cos(delta)*(b*sin(delta)+sqrt(R^2-(b*cos(delta))^2));
    y4=-tan(delta)*x4+b;
    line([x3,x4],[y3,y4],'color','k')
    delta=2*(th-phi+alfa-beta);
    b=y4+tan(delta)*x4;
    x5=x4+0.2;
    y5=-tan(delta)*x5+b;
    line([x4,x5],[y4,y5],'color','k')
end
hold off
axis equal
axis off
grid on

Representamos el ángulo de desviación δ₃=2(θ-φ+β-γ) en función del ángulo incidente θ en el intervalo 0<θ<arcsin(nR/r).

${\displaystyle {\delta }_3=2\left(\theta -\arcsin \left(\frac{\sin \theta }{n_0}\right)+\arcsin \left(\frac{R}{r}\frac{\sin \theta }{n_0}\right)-\arcsin \left(\frac{R}{r}\frac{\sin \theta }{n}\right)\right)}$

R=1; %radio exterior
r=0.5; %radio interior
n0=1.5; %índice de refracción
n=1.33; %índice de refración del agua
th_lim=asin(n*r/R);
f=@(x) 2*(x-asin(sin(x)/n0))+2*(asin(R*sin(x)/(r*n0))-asin(R*sin(x)/(r*n)));
fplot(f,[0, th_lim])
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','15','30','45','60','75','90'})
set(gca,'YTick', -pi/24:pi/24:pi/25)
set(gca,'YTickLabel',{'-7.5','0','7.5'})
grid on
ylim([-0.15,0.15])
xlabel('\theta')
ylabel('\delta')
title('Angulo de desviación, rayo 3')

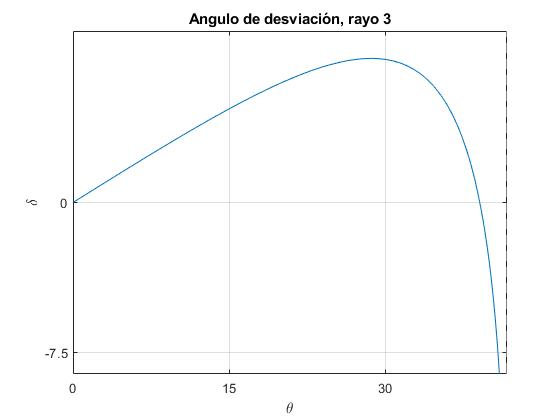
Vemos que es una función que tiene un máximo que se calcula

${\displaystyle \frac{d{\delta }_3}{d\theta }=2\left(1-\frac{\frac{\cos \theta }{n_0}}{\sqrt{1-\frac{{\sin }^2\theta }{n_0^2}}}+\frac{\frac{R}{r}\frac{\cos \theta }{n_0}}{\sqrt{1-\frac{R^2}{r^2}\frac{{\sin }^2\theta }{n_0^2}}}-\frac{\frac{R}{r}\frac{\cos \theta }{n}}{\sqrt{1-\frac{R^2}{r^2}\frac{{\sin }^2\theta }{n^2}}}\right)=0}$

Se trata de una ecuación transcendente con dos incógnitas: el ángulo de incidencia θ correspondiente al máximo de δ₃ y n (índice de refracción del líquido contenido en el tubo capilar)

Designamos por α₃ el ángulo de desviación, para este ángulo de incidencia

${\displaystyle {\alpha }_3=2\left({\theta }_m-\arcsin \left(\frac{\sin \theta }{n_0}\right)+\arcsin \left(\frac{R}{r}\frac{\sin \theta }{n_0}\right)-\arcsin \left(\frac{R}{r}\frac{\sin \theta }{n}\right)\right)}$

Conocida la medida del ángulo α₃ despejamos las dos incógnitas: θ y n, en el sistema de dos ecuaciones no lineales que se pueden resolver de forma gráfica o mediante el comando fsolve

Los ángulos de dispersión

Representamos con una línea gruesa de color rojo, el haz incidente sobre un tubo capilar de diámetro 1 mm. Se representan los rayos dispersados mediante líneas de color rojo en las tres direcciones estudiadas, marcándose en color azul los ángulos de desviación α₁, α₂ y α₃, que se miden en el sentido de las agujas del reloj. La pantalla cilíndrica representada por la circunferencia de color negro tiene un radio de 7.5 cm

R=1; %radio exterior
r=0.5; %radio interior
n0=1.5; %índice de refracción
n=1.33; %índice de refración del agua
Rp=75; %radio de la pantalla
fplot(@(x) Rp*cos(x), @(x) Rp*sin(x),[0,2*pi],'color','k')
th_lim=asin(n0*r/R);
d_lim=R*sin(th_lim);
for i=1:9
    d=d_lim+(R-d_lim)*i/10;
    th=asin(d/R);
    delta=2*(th-asin(sin(th)/n0));
    line([0,Rp*cos(delta)],[0,-Rp*sin(delta)],'color','r')
end
alfa=2*(asin(n0*r/R)-asin(r/R));
line([0,Rp*cos(alfa)],[0,-Rp*sin(alfa)],'color','b')

for i=1:9
    d=d_lim+(R-d_lim)*i/10;
    th=asin(d/R);
    delta=pi+2*th-4*asin(sin(th)/n0);
    line([0,Rp*cos(delta)],[0,-Rp*sin(delta)],'color','r')
end
th=asin(sqrt((4-n0^2)/3));
alfa=pi+2*th-4*asin(sin(th)/n0);
line([0,Rp*cos(alfa)],[0,-Rp*sin(alfa)],'color','b')

th_lim=asin(n*r/R);
d_lim=R*sin(th_lim);
for i=1:9
    d=d_lim*i/10;
    th=asin(d/R);
    delta=2*(th-asin(sin(th)/n0)+asin(R*sin(th)/(r*n0))-asin(R*sin(th)/(r*n)));
    line([0,Rp*cos(delta)],[0,-Rp*sin(delta)],'color','r')
end
f=@(x) 1-cos(x)/(n0*sqrt(1-(sin(x)/n0)^2))+R*cos(x)/(r*n0*sqrt(1-(R*sin(x)
/(r*n0))^2))-R*cos(x)/(r*n*sqrt(1-(R*sin(x)/(r*n))^2));
th=fzero(f,delta);
alfa=2*(th-asin(sin(th)/n0)+asin(R*sin(th)/(r*n0))-asin(R*sin(th)/(r*n)));
line([0,Rp*cos(alfa)],[0,-Rp*sin(alfa)],'color','b')

line([-Rp-10,0],[0,0],'color','r','lineWidth',2)
axis equal
axis off

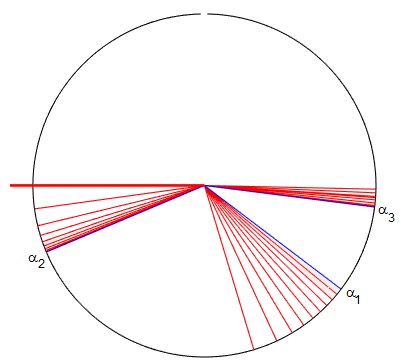
Medida del índice de refracción de un líquido

En el tubo capilar se ha introducido agua, alcohol y simeticona (un medicamento). Los ángulo medidos son

1. La medida de α₂ proporciona el índice de refracción del tubo, n₀

${\displaystyle {\alpha }_2=\pi +2\arcsin \left(\sqrt{\frac{4-n_0^2}{3}}\right)-4\arcsin \left(\frac{1}{n_0}\sqrt{\frac{4-n_0^2}{3}}\right)}$

alfa_2=(154+47/60)*pi/180;
f=@(x) pi+2*asin(sqrt((4-x.^2)/3))-4*asin(sqrt((4-x.^2)/3)./x)-alfa_2;
fplot(f,[1,1.7])
grid on
xlabel('f(n_0)')
xlabel('n_0')
grid on
title('Indice de refracción del tubo')



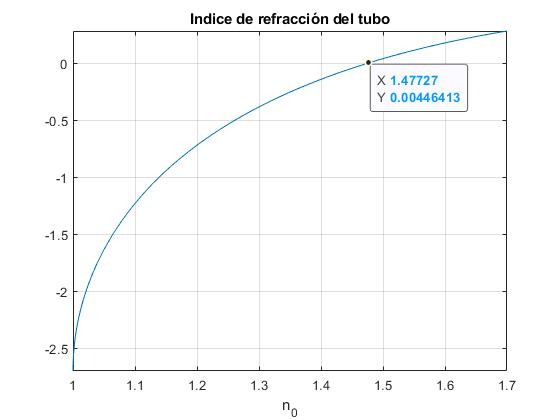
El resultado es n₀=1.477

2. La medida de α₁ nos proporciona el valor del cociente r/R, donde r es el radio interior del tubo y R el exterior

${\displaystyle {\alpha }_1=2\left(\arcsin \left(\frac{n_{0}r}{R}\right)-\arcsin \left(\frac{r}{R}\right)\right)}$

alfa_1=(37+33/60)*pi/180;
n0=1.477; %índice de refracción del tubo
f=@(x) 2*(asin(n0*x)-asin(x))-alfa_1;
fplot(f,[0,1])
grid on
xlabel('f(r/R)')
xlabel('r/R')
grid on
title('Cociente r/R de los radios del tubo')



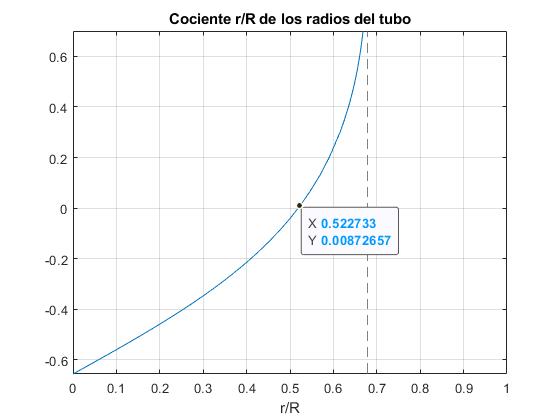
El resultado es r/R=0.5227

3. La medida de α₃ nos proporciona el valor del índice de refracción n del líquido contenido en el tubo capilar. Para ello hay que resolver el sistema no lineal de dos ecuaciones con dos incógnitas: θ y n

${\displaystyle \{\begin{array}{l}1-\frac{\cos \theta }{\sqrt{n_0^2-{\sin }^2\theta }}+\frac{R}{r}\frac{\cos \theta }{\sqrt{n_0^2-\frac{R^2}{r^2}{\sin }^2\theta }}-\frac{R}{r}\frac{\cos \theta }{\sqrt{n^2-\frac{R^2}{r^2}{\sin }^2\theta }}=0\\ 2\left(\theta -\arcsin \left(\frac{\sin \theta }{n_0}\right)+\arcsin \left(\frac{R}{r}\frac{\sin \theta }{n_0}\right)-\arcsin \left(\frac{R}{r}\frac{\sin \theta }{n}\right)\right)-{\alpha }_3=0\end{array}}$

Representamos gráficamente las funciones f(θ,n) y g(θ,n) y obtenemos la ordenada n del punto de intersección

alfa_3=(9+17/60)*pi/180;
n0=1.477; %índice de refracción del tubo
r_R=0.5227; %relación radios
f=@(x,y) 1-cos(x)./sqrt(n0^2-sin(x).^2)+cos(x)./(r_R*sqrt(n0^2-
(sin(x)/r_R).^2))
-cos(x)./(r_R.*sqrt(y.^2-(sin(x)/r_R).^2));
g=@(x,y) 2*(x-asin(sin(x)/n0)+asin(sin(x)/(r_R*n0))-asin(sin(x)./(r_R*y)))-
alfa_3;
hold on
fimplicit(f, [0,pi/4,1,n0])
fimplicit(g, [0,pi/4,1,n0])
hold off
xlabel('\theta')
ylabel('n')
grid on
title('Indice de refracción de un líquido')



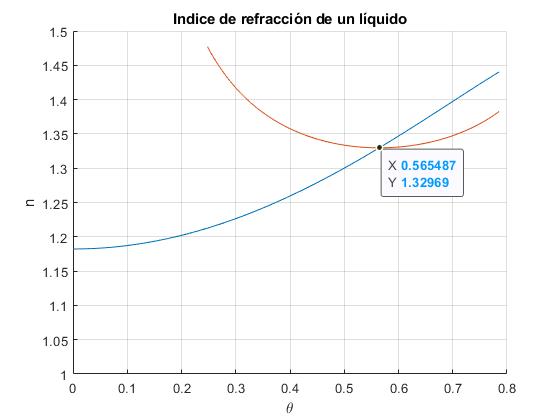
El resultado es n=1.3297

Se sugiere al lector probar con los otros dos líquidos. El índice de refracción del tubo no cambia n₀=1.477. El cociente de los dos radios tampoco cambia r/R=0.5227. El índice de refracción del alcohol es n=1.3609 y de la simeticona n=1.4056

Referencias

M. F. Duque D., S. Gómez P., C. C. Pinilla C. Refractómetro de cubeta de sección cuadrada. Revista Mexicana de Física E 52 (2) 177–181. Diciembre 2006

I E Santosa. Measuring refractive index of a liquid with a spherical shape flask and Tracker. Phys. Educ. 56 (2021) 065014

Zhihong You, Daya Jiang, Zhibo Hou, Jinghua Xiao. Analysis of light scattered by a capillary to measure a liquid’s index of refraction. Am. J. Phys. 80 (8), August 2012, pp. 688-693