Representamos la pecera por una esfera de plástico transparente o de vidrio de radio R, llena de agua. Supondremos que el recipiente está hecho de un material de pequeño espesor que no afecta a la marcha de los rayso de luz. El índice de refracción de la esfera es n₁ que es el del agua y el índice de refracción del aire es n₂

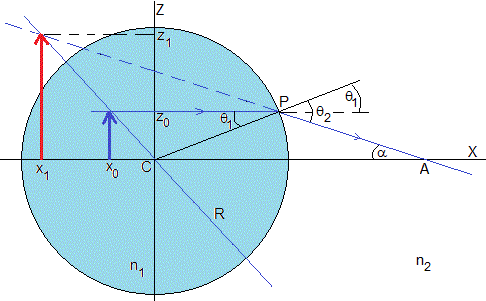
Situamos el origen en el centro C de la pecera y los ejes X (horizontal) y Z (vertical)

Vamos a determinar la posición x₁ y tamaño z₁ de la imagen (flecha de color rojo) del pez representado por una flecha vertical azul de altura z₀, situada en la posición x₀

Trazamos un rayo de luz que pasa por el origen C, que no se desvía al pasar del agua al aire.

Trazamos otro paralelo al eje X, que se refracta en el punto P. El ángulo del rayo incidente es θ₁ y el refractado es θ₂. La ley de Snell de la refracción es

${\displaystyle \[ n_1\sin {\theta }_1=n_2\sin {\theta }_2 \]}$

El ángulo incidente θ₁ tiene un valor límite que es aquél para el cual θ₂=π/2, reflexión total

${\displaystyle \sin {\theta }_c=\frac{n_2}{n_1}}$

Dado el valor del radio R de la pecera, la altura del objeto z₀<Rsinθ_c

La posición y tamaño de la imagen virtual se obtiene de la intersección del rayo que pasa por el centro de la esfera y de la prolongación del rayo refractado en el punto P

La ecuación de la recta z=mx+b que pasa por el centro C de la esfera y por el punto (x₀, z₀) es

${\displaystyle \begin{array}{l}b=0\\ z=mx\\ z_0=m{x}_0,m=\frac{z_0}{x_0}\\ z=\frac{z_0}{x_0}x\end{array}}$

Determinamos la ecuación de la recta que pasa por el punto P y forman un ángulo π-α con el eje X. La pendiente m es

${\displaystyle m=\tan \left(\pi -\alpha \right)=-\tan \left({\theta }_2-{\theta }_1\right)}$

La ordenada en el origen b se determina, sabiendo que pasa por el punto P $\left(\sqrt{R^2-z_0^2},z_0\right)$

${\displaystyle z_0=-\tan \left({\theta }_2-{\theta }_1\right)\sqrt{R^2-z_0^2}+b}$

La ecuación de la recta es

${\displaystyle \begin{array}{l}z=-\tan \left({\theta }_2-{\theta }_1\right)x+z_0+\tan \left({\theta }_2-{\theta }_1\right)\sqrt{R^2-z_0^2}\\ z=z_0-\tan \left({\theta }_2-{\theta }_1\right)\left(x-\sqrt{R^2-z_0^2}\right)\end{array}}$

La intersección de ambas rectas nos da la posición x₁ y la altura z₁ de la imagen

${\displaystyle \begin{array}{l}\{\begin{array}{l}z=z_0-\tan \left({\theta }_2-{\theta }_1\right)\left(x-\sqrt{R^2-z_0^2}\right)\\ z=\frac{z_0}{x_0}x\end{array}\\ x_1=\frac{z_0+\tan \left({\theta }_2-{\theta }_1\right)\sqrt{R^2-z_0^2}}{\frac{z_0}{x_0}+\tan \left({\theta }_2-{\theta }_1\right)}\\ z_1=\frac{z_0}{x_0}{x}_1\end{array}}$

Representamos la recta que pasa por el centro y la prolongación del rayo refractado. El objeto (en azul) y la imagen (en rojo)

n1=4/3; %agua
n2=1; %aire
z0=2/15; %tamaño del objeto
R=1; %radio de la esfera
x0=-0.5; %posición del obejto
hold on
th=linspace(0,360)*pi/180;
fill(cos(th),sin(th),'c')

fplot(@(t) cos(t), @(t) sin(t),[0,2*pi])
m=z0/x0;
line([-2,1],[-2*m,m])
th_1=asin(z0/R);
th_2=asin(n1*sin(th_1)/n2);
m=tan(th_2-th_1);
line([-2,2],[z0-m*(-2-sqrt(R^2-z0^2)),z0-m*(2-sqrt(R^2-z0^2))])
x1=(z0+m*sqrt(R^2-z0^2))/(z0/x0+m);
z1=z0*x1/x0;
line([x0,x0],[0,z0],'lineWidth',1.5,'color','b') %objeto
line([x1,x1],[0,z1],'lineWidth',1.5,'color','r') %imagen
hold off
grid on
axis equal
xlabel('x_0/R')
ylabel('M')
title('Objeto e imagen')

• La posición del objeto es x₀=-0.5



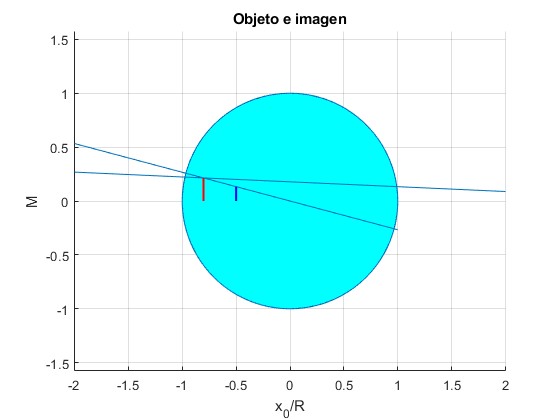
La posición de la imagen es x₁=-0.80 y su tamaño, z₁=0.21

>> x1,z1
x1 =   -0.8029
z1 =    0.2141

• La posición del objeto es x₀=0.4



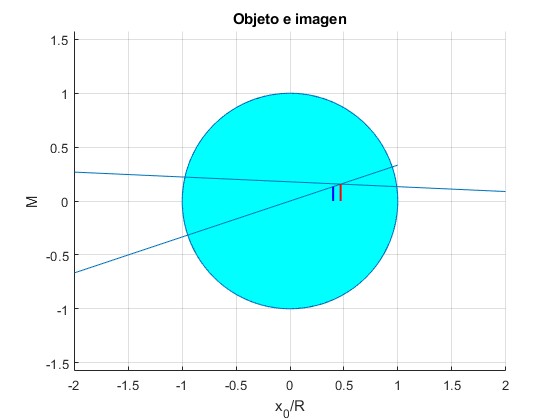
La posición de la imagen es x₁=0.47 y su tamaño, z₁=0.16

>> x1,z1
x1 =    0.4703
z1 =    0.1568

Posición de la imagen

Expresamos la posición x₁ y tamaño z₁ de la imagen en términos de la posición x₀/R y tamaño z₀/R del objeto y del cociente de los índices de refracción n₂/n₁ (aire y agua)

${\displaystyle \begin{array}{l}\sin {\theta }_1=\frac{z_0}{R},\tan {\theta }_1=\frac{\sin {\theta }_1}{\sqrt{1-{\sin }^2{\theta }_1}}=\frac{\frac{z_0}{R}}{\sqrt{1-{\left(\frac{z_0}{R}\right)}^2}}=\frac{z_0}{\sqrt{R^2-z_0^2}}\\ \tan {\theta }_2=\frac{\sin {\theta }_2}{\sqrt{1-{\sin }^2{\theta }_2}}=\frac{\frac{n_1}{n_2}\sin {\theta }_1}{\sqrt{1-\frac{n_1^2}{n_2^2}{\sin }^2{\theta }_1}}=\frac{\frac{n_1}{n_2}\frac{z_0}{R}}{\sqrt{1-\frac{n_1^2}{n_2^2}\frac{z_0^2}{R^2}}}=\frac{n_1{z}_0}{\sqrt{n_2^2{R}^2-n_1^2{z}_0^2}}\\ \tan \left({\theta }_2-{\theta }_1\right)=\frac{\tan {\theta }_2-\tan {\theta }_1}{1-\tan {\theta }_2\tan {\theta }_1}=\frac{\frac{n_1{z}_0}{\sqrt{n_2^2{R}^2-n_1^2{z}_0^2}}-\frac{z_0}{\sqrt{R^2-z_0^2}}}{1-\frac{n_1{z}_0}{\sqrt{n_2^2{R}^2-n_1^2{z}_0^2}}\frac{z_0}{\sqrt{R^2-z_0^2}}}=z_0\frac{n_1\sqrt{R^2-z_0^2}-\sqrt{n_2^2{R}^2-n_1^2{z}_0^2}}{\sqrt{n_2^2{R}^2-n_1^2{z}_0^2}\sqrt{R^2-z_0^2}-n_1{z}_0^2}\\ x_1=x_0\frac{z_0+\tan \left({\theta }_2-{\theta }_1\right)\sqrt{R^2-z_0^2}}{z_0+x_0\tan \left({\theta }_2-{\theta }_1\right)}=x_0\frac{z_0+z_0\frac{n_1\sqrt{R^2-z_0^2}-\sqrt{n_2^2{R}^2-n_1^2{z}_0^2}}{\sqrt{n_2^2{R}^2-n_1^2{z}_0^2}\sqrt{R^2-z_0^2}-n_1{z}_0^2}\sqrt{R^2-z_0^2}}{z_0+x_0{z}_0\frac{n_1\sqrt{R^2-z_0^2}-\sqrt{n_2^2{R}^2-n_1^2{z}_0^2}}{\sqrt{n_2^2{R}^2-n_1^2{z}_0^2}\sqrt{R^2-z_0^2}-n_1{z}_0^2}}\\ x_1=x_0\frac{\sqrt{n_2^2{R}^2-n_1^2{z}_0^2}\sqrt{R^2-z_0^2}-n_1{z}_0^2+\left(n_1\sqrt{R^2-z_0^2}-\sqrt{n_2^2{R}^2-n_1^2{z}_0^2}\right)\sqrt{R^2-z_0^2}}{\sqrt{n_2^2{R}^2-n_1^2{z}_0^2}\sqrt{R^2-z_0^2}-n_1{z}_0^2+x_0\left(n_1\sqrt{R^2-z_0^2}-\sqrt{n_2^2{R}^2-n_1^2{z}_0^2}\right)}=\\ \frac{x_1}{R}=\frac{x_0}{R}\frac{\sqrt{{\left(\frac{n_2}{n_1}\right)}^2-{\left(\frac{z_0}{R}\right)}^2}\sqrt{1-{\left(\frac{z_0}{R}\right)}^2}-{\left(\frac{z_0}{R}\right)}^2+\left(\sqrt{1-{\left(\frac{z_0}{R}\right)}^2}-\sqrt{{\left(\frac{n_2}{n_1}\right)}^2-{\left(\frac{z_0}{R}\right)}^2}\right)\sqrt{1-{\left(\frac{z_0}{R}\right)}^2}}{\sqrt{{\left(\frac{n_2}{n_1}\right)}^2-{\left(\frac{z_0}{R}\right)}^2}\sqrt{1-{\left(\frac{z_0}{R}\right)}^2}-{\left(\frac{z_0}{R}\right)}^2+\frac{x_0}{R}\left(\sqrt{1-{\left(\frac{z_0}{R}\right)}^2}-\sqrt{{\left(\frac{n_2}{n_1}\right)}^2-{\left(\frac{z_0}{R}\right)}^2}\right)}\end{array}}$

Representamos la posición x₁/R de la imagen de un objeto de altura z₀/R=2/15, en función de la posición del objeto en el intervalo $-\sqrt{1-z_0^2}<x_0<\sqrt{1-z_0^2}$. El cociente de los índices de refracción, n₂/n₁=3/4

n=3/4; %n2/n1=aire/agua
z0=2/15; %altura objeto
x1=@(x) x*(sqrt(n^2-z0^2)*sqrt(1-z0^2)-z0^2+(sqrt(1-z0^2)-sqrt(n^2-z0^2))*
sqrt(1-z0^2))./(sqrt(n^2-z0^2)*sqrt(1-z0^2)-z0^2+x*(sqrt(1-z0^2)-sqrt(n^2-z0^2)));
fplot(x1,[-sqrt(1-z0^2),sqrt(1-z0^2)])
line([-sqrt(1-z0^2),sqrt(1-z0^2)],[-sqrt(1-z0^2),sqrt(1-z0^2)],'color','k')
grid on
xlabel('x_0/R')
ylabel('x_1/R')
title('Posición x/R')

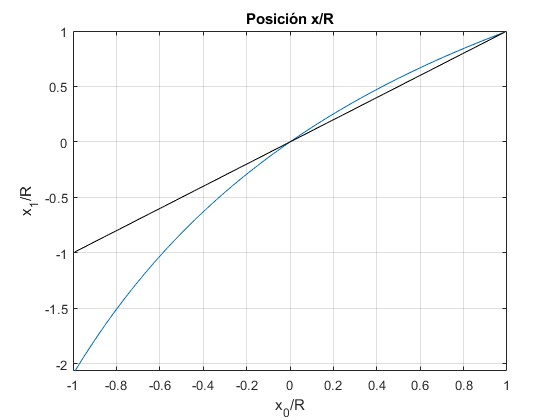
Comparando la representación de x₁/R en color azul, con la recta x₁/R=x₀/R, en color negro, apreciamos

• En el intervalo, $0<x_0<\sqrt{1-z_0^2}$, la imagen del pez aparece más cercana x₁>x₀ al observador A
• En el intervalo, $-\sqrt{1-z_0^2}<x<0$, la imagen del pez aparece más alejada x₁<x₀ del observador A
• En x₀=0, la posición de la imagen coincide con el objeto

Aumento

La altura z₁ de la imagen es $z_1=\frac{z_0}{x_0}{x}_1$

El aumento M

${\displaystyle M=\frac{z_1}{z_0}=\frac{x_1}{x_0}}$

Representamos el aumento M en función de la posición x₀ del objeto

n=3/4; %n2/n1
z0=2/15;
M=@(x) (sqrt(n^2-z0^2)*sqrt(1-z0^2)-z0^2+(sqrt(1-z0^2)-sqrt(n^2-z0^2))*
sqrt(1-z0^2))./(sqrt(n^2-z0^2)*sqrt(1-z0^2)-z0^2+x*(sqrt(1-z0^2)-sqrt(n^2-z0^2)));
fplot(M,[-sqrt(1-z0^2),sqrt(1-z0^2)])
grid on
xlabel('x_0/R')
ylabel('M')
title('Aumento')

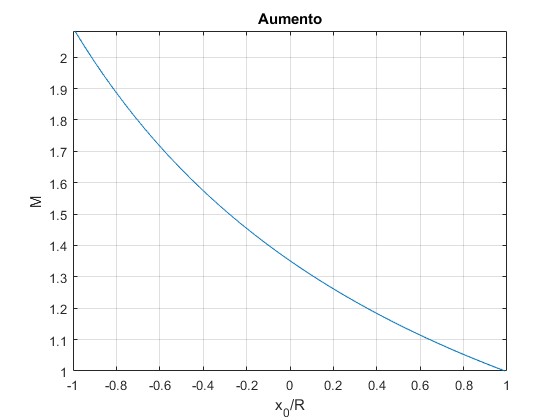
El tamaño de la imagen se incrementa con x₀, a medida que el pez se aleja del observador A

Referencias

R De Luca. Watching a goldfish swimming in a fishbowl. Phys. Educ. 60 (2025) 055005