Propagación en un medio no homogéneo (III)
El índice de refracción varía con y
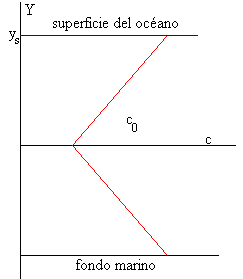
En la figura, se muestra la variación de la velocidad del sonido c con la profundidad y para el caso en que el mínimo c0 de velocidad se encuentre a medio camino entre la superficie del océano y el fondo marino. Situamos el origen de coordenadas en dicha posición, de modo que la superficie se encuentra a +ys y el fondo a –ys.
La velocidad del sonido para y>0 es c=c0+by donde b es la pendiente de la recta o gradiente de la velocidad del sonido con la profundidad y.
En un medio estratificado verticalmente la ley de Snell se expresa
n0·sinθ0= n1·sinθ1
n1·sinθ1= n2·sinθ2
n2·sinθ2=n3·sinθ3
En general
n0·sinθ0=n(y)sinθ
donde n0 es el índice de refracción para y=0, y n(y) es el índice de refracción a la altura y. θ es el ángulo que forma el rayo incidente con la normal tal como se aprecia en la figura
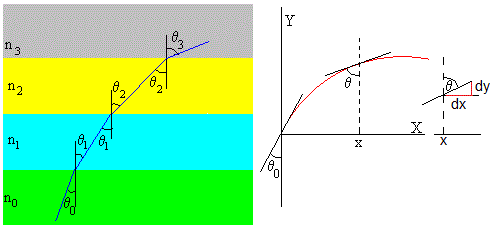
La ley de Snell se expresa en términos de las velocidades de propagación del sonido
Ecuación de la trayectoria
En la parte derecha de la figura, vemos
Integramos
donde C es una constante de integración que se determina a partir de las condiciones iniciales, para x=0, y=0, el rayo parte del origen.
Elevando al cuadrado
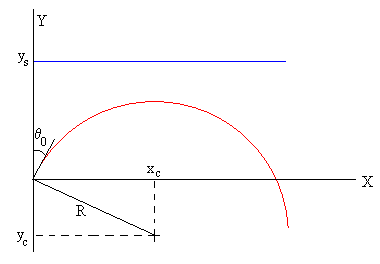
Que es la ecuación de una circunferencia centrada en el punto xc, yc y de radio R
Variando el ángulo inicial θ0 obtenemos distintas trayectorias.
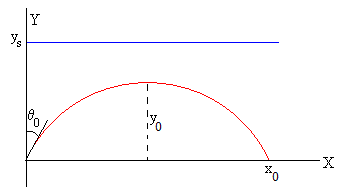
El arco de circunferencia corta al eje X en el punto y=0, cuya abscisa es
La altura máxima del rayo se produce para x0/2
El rayo alcanza la superficie del agua ys para el ángulo θ0 tal que y0=ys
Trayectorias
Para que un rayo llegue a la posición (x0, 0) sobre el eje X hay varias posibilidades
Un arco de semicircunferenciaEn la figura de la izquierda, se muestra la trayectoria que une el origen y el punto (x0, 0) mediante un arco de semicircunferencia. Calculamos el ángulo θ0
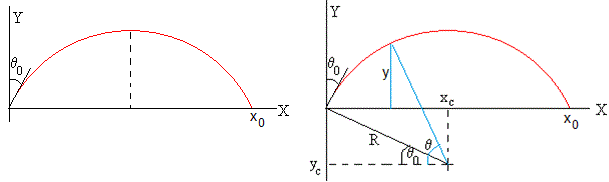
El tiempo que tarda el sonido en propagarse desde el origen hasta el punto (x0, 0), es el doble del tiempo que tarda en ir desde el origen hasta el máximo (x0/2, y0). Si c es la velocidad del sonido. El tiempo que tarda en recorrer el arco de circunferencia ds=R·dθ es ds/c, el tiempo total es
Como c=c0+by. En la figura de la derecha, y-yc=R·sinθ, por lo que y+c0/b=R·sinθ
Para resolver esta integral se hace el cambio de variable x=tan(θ/2)
Ejemplo: x0=10000 m, c0=1500 m/s, b=0.02 s-1. Obtenemos θ0=86.19°, t=6.662 s
n arcos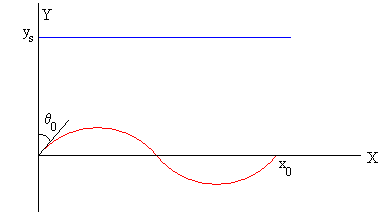
La segunda posibilidad es describir dos arcos de circunferencia, uno por encima y otro por debajo del eje X.
En esta ocasión xmáx=x0/2 y el ángulo θ0 es
Tres arcos de semicircunferencia, cuatro, …n arcos
Ejemplo
Sea c0=1500 m/s la velocidad del sonido en la posición del eje X, a medio camino entre la superficie y el fondo del océano
Sea el gradiente de velocidad con la altura b=0.2 s-1, se el ángulo θ0=60º que forma el rayo incidente con el eje Y. El fondo del océano se encuentra a 10000 m de profundidad o bien, 5000 m por debajo del eje X.
La altura máxima del rayo es
La primera intersección con el eje X se produce a la distancia
Las otras son múltiplos de esta cantidad
El mínimo ángulo θ0 por debajo del cual el rayo ya no describe arcos de circunferencia sino que es absorbido por el fondo del océano.
Nota: El rayo no se dirige hacia la superficie del océano para evitar tratar con la refracción de dicho rayo en la superficie de separación entre el aire y el agua. Unos rayos se refractarán y otros experimentarán reflexión total hacia el interior del océano.
Dirigiéndolos hacia abajo, supondremos que el sonido es absorbido al llegar al fondo del océano.
Actividades
Se introduce
- El gradiente b de incremento de la velocidad del sonido en el agua con la altura y, en el control titulado Gradiente b.
- El ángulo θ0 que forma el rayo con el eje Y, cuando pasa por el origen, en el control titulado Ángulo
- Se ha fijado la posición del fondo del océano en ys=-5000 m
Se pulsa el botón titulado Nuevo.
La intensidad de color azul señala la magnitud de la velocidad de propagación: mínima en el eje X, aumentando hacia la superficie del océano y hacia el fondo. El índice de refracción, que es inversamente proporcional a la velocidad de propagación, es máximo a lo largo del eje X y disminuye hacia la superficie del océano y hacia el fondo.
Vemos que el efecto de dicho gradiente es que el sonido se propague a lo largo de arcos de circunferencia a través de una especie de canal.
La velocidad del sonido cambia con la altura
En la parte inferior de la atmósfera, la temperatura decrece con la altura. Supondremos que decrecimiento es lineal
Donde T0 es la temperatura al nivel del mar, y=0 y b=0.023·10-3 m-1
La velocidad del sonido es
Sabiendo que T0=293 K (20 °C), índice adiabático, γ=1.4, constante de los gases, R=8.314 J/(K·mol) y masa molecular del aire, M=28.95·10-3 kg/mol. La velocidad del sonido a nivel del mar es c=343.2 m/s
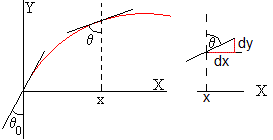
El índice de refracción de un medio es inversamente proporcional a la velocidad de propagación en dicho medio. La ley de la refracción se espresa
Despejamos la altura y y derivamos dy
La ecuación diferencial de la trayectoria (véase la parte derecha de la figura)
donde C es una constante de integración que se determina a partir de las condiciones iniciales. En este caso son, x=0, θ=θ0=π/2. Por tanto, C=π/(2b)
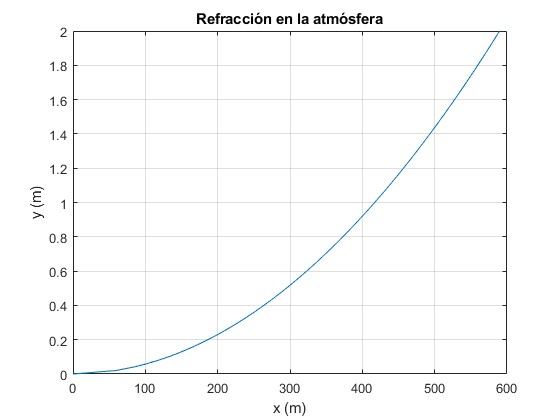
Por ejemplo, para y=2 m, calculamos el ángulo θ=89.6° y después, x=589.76 m
b=0.023e-3;
y=linspace(0,2,100);
th=acos(sqrt(b*y));
x=pi/(2*b)-(th-sin(2*th)/2)/b;
plot(x,y)
grid on
xlabel('x (m)')
ylabel('y (m)')
title('Refracción en la atmósfera')
El índice de refracción varía con x
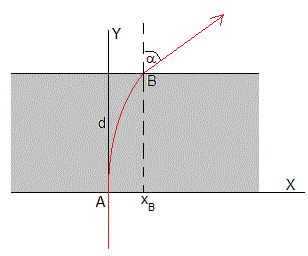
Consideremos una placa plana-paralela transparente de espesor d, cuyo índice de refracción n varía con la abscisa x de la forma
Un haz de luz incide en A, (xA=0) y emerge en el punto B (xB) haciendo un ángulo α. Calcular
- el índice de refracción nB de la placa en la posición xB
- La posición xB del rayo emergente
- El espesor d de la placa.
Datos: n0=1.2, R=13 y α=30°
Medio estratificado
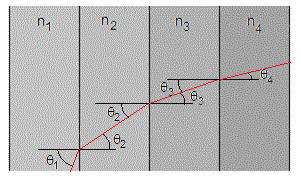
En un medio estratificado se cumple que
n1sinθ1=n2sinθ2=n3sinθ3=n4sinθ4
En general, nsinθ=n0sin90°
n y θ son funciones de la abscisa x. n0 es el índice de refracción en A, (x=0). En esta posición, el rayo incide perpendicularmente a la placa, θ=90°
Rayo emergente
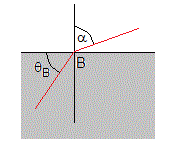
El rayo emerge en el punto B, en la superficie de separación entre la placa y el aire (indice de refracción 1) se cumple, nBsin(90-θB)=1·sinα
Despejamos nB
Con los datos del problema nB=1.3
Calculamos xB a partir de nB
Con los datos del problema xB=1 cm
Ecuación de la trayectoria
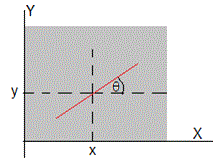
La ley de la refracción se escribe, nsinθ=n0 en este medio estratificado. Donde n y θ son funciones de x
La pendiente θ de la trayectoria del rayo de luz en el punto (x,y) es
Expresamos la pendiente dy/dx en una función de x
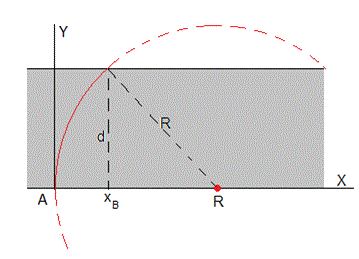
Integramos para obtener la ecuación de la trayectoria y=f(x), sabiendo que el rayo pasa por el origen, x=0, y=0
La ecuación de la trayectoria seguida por el rayo de luz es un arco de circunferencia centrada en x=R, y=0.
El espesor d de la placa es lado del triángulo rectángulo de la figura
Con los datos del problema, d=4.8 cm
Referencias
Problema de la VII Olimpiada Internacional de Física. Varsovia, 1974
Solutions of Indian National Physics Olympiad – 2019. Problem 1, pp. 1-2
Problema de la XXVI Olimpiada Internacional de Física. Canberra, 1995

