Optica paraxial
Espejo esférico cóncavo
Vamos a calcular la posición s’ y tamaño h’ de la imagen producida por un espejo esférico cóncavo de radio r, de un objeto de altura h situado a una distancia s del origen.
La imagen se produce en la intersección del rayo reflejado y del rayo que pasa por el centro del espejo. Se trata de la intersección de dos rectas cuyas ecuaciones vamos a calcular seguidamente.
En primer lugar, establecemos el origen en O y tomamos como positivo el eje X hacia la izquierda.
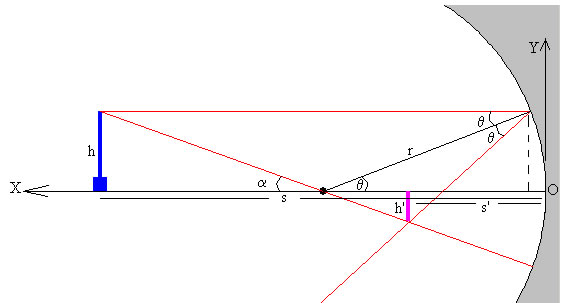
Como vemos en la figura, el rayo incidente y el rayo reflejado forman un ángulo θ con la dirección radial (normal a la superficie).
-
El rayo reflejado parte del punto x1=r(1-cosθ), y1=r·sinθ, y forma un ángulo con el eje X de 180-2·θ.
La ecuación de la recta es, y=ax+b, donde a es la pendiente (tangente del ángulo que forma con el eje X) y b la ordenada en el origen.
y=-tan(2θ)·x+b, el parámetro b se determina de la condición de que la recta pasa por el punto (x1, y1), y1=-tan(2θ)·x1+b
y=-tan(2θ)·x+ r·sinθ+r·tan(2θ)·(1-cosθ). El valor del ángulo θ es sinθ=h/r
El segundo rayo corresponde a una recta que pasa por el centro de coordenadas x1=r, y1=0 y que forma un ángulo α con el eje X.
La ecuación de esta recta es y=tanα·x-r·tanα
El valor del ángulo α es tanα=h/(s-r)
Despejamos x en el sistema de ecuaciones
Esta es la posición s’ de la imagen y su tamaño h’ se calcula tomado cualquiera de las ecuaciones de las dos rectas h’=tanα·s’-r·tanα
Objeto: Posición, s=20, tamaño, h=2
Radio del espejo esférico, r=10
Calculamos los ángulos
Imagen: Posición, s’=6.52, tamaño, h’=0.7
Utilizamos MATLAB para hacer los cálculos
s=20; %posición del objeto
h=2; %altura del objeto
r=10; %radio del espejo
theta=asin(h/r);
alfa=atan(h/(s-r));
%posición de la imagen
sp=r*(tan(alfa)+sin(theta)+tan(2*theta)*(1-cos(theta)))
/(tan(alfa)+tan(2*theta));
%altura de la imagen
hp=(sp-r)*tan(alfa);
fprintf('Posición %2.2f y altura %2.2f de la imagen\n',sp,hp)
Posición 6.53 y altura -0.69 de la imagen
No se forma imagen cuando el objeto se encuentra en el centro del espejo
Aproximación paraxial
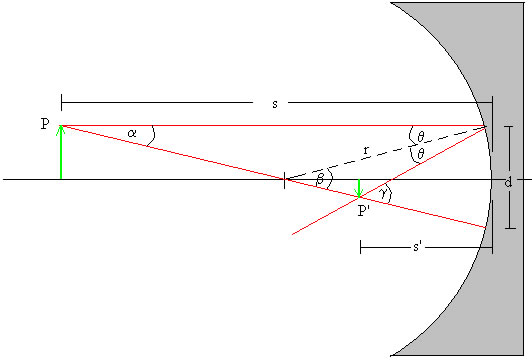
La figura muestra la trayectoria de dos rayos de luz que parten del punto P (objeto) y después de reflejarse en el espejo esférico de radio r, convergen en el punto P’ (imagen). Uno de los rayos es paralelo al eje horizontal y el otro rayo pasa por el centro del espejo, es normal a su superficie.
Queremos obtener una ecuación que relacione la posición del punto imagen s’ con la del punto objeto s.
En la figura vemos que β=α+θ y que γ=α+2θ
Eliminando el ángulo θ en las dos ecuaciones, tenemos γ=2β-α
Con las aproximaciones
Supondremos que el segmento d es un arco de radio r y ángulo de apertura β, por lo que d=r·β
Esta es la ecuación que relaciona las distancias del objeto y la imagen con el radio de curvatura del espejo esférico.
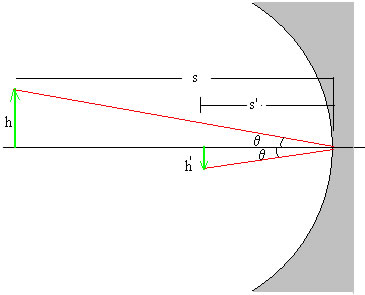
Se define aumento m como el cociente entre el tamaño de la imagen y’ y la del objeto y. m=h’/h. Utilizando la relación de semejanza entre los dos triángulos
El signo negativo indica que P y P’ están en lados opuestos al eje X
Superficie esférica convexa
Vamos a calcular la posición s’ y tamaño h’ de la imagen producida por una superficie esférica convexa de radio r que separa dos medios de distinto índice de refracción n1 y n2, de un objeto de altura h situado a una distancia s del origen.
La imagen se produce en la intersección del rayo refractado y del rayo que pasa por el centro de la superficie esférica. Es la intersección de dos rectas cuyas ecuaciones vamos a calcular seguidamente.
En primer lugar, establecemos el origen en O y tomamos como positivo el eje X hacia la derecha.
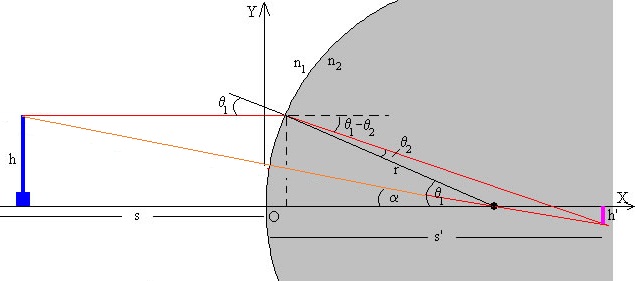
Como vemos en la figura, el rayo incidente forma un ángulo θ1 y el ángulo reflejado forma un ángulo θ2 con la dirección radial (normal a la superficie). De acuerdo con la ley de Snell de la refracción, n1·sin θ1 =n2·sinθ2
-
El rayo refractado parte del punto x1=r(1-cosθ1), y1=r·sinθ1, y forma un ángulo con el eje X de 180-(θ1- θ2)
La ecuación de la recta es, y=-tan(θ1- θ2)·x+b, el parámetro b se determina de la condición de que la recta pasa por el punto (x1, y1) y1=-tan(θ1- θ2)·x1+b
y=-tan(θ1- θ2)·x+ r·sinθ1+r·tan(θ1- θ2)·(1-cosθ1)
El valor del ángulo θ1 es sinθ1=h/r El segundo rayo corresponde a una recta que pasa por el centro de coordenadas x1=r, y1=0 y que forma un ángulo 180-α con el eje X.
La ecuación de esta recta es y=-tanα·x+r·tanα
El valor del ángulo α es tanα=h/(-s+r), el signo de s es negativo ya que está a la izquierda del origen.Despejamos x en el sistema de ecuaciones
Esta es la posición s’ de la imagen y su tamaño h’ se calcula tomado cualquiera de las ecuaciones de las dos rectas
h’=-tanα·s’+r·tanα
Se obtiene una imagen virtual, prolongación de los rayos cuando θ1 -θ2≤α
Objeto: Posición, s=-10, tamaño, h=2
Radio del dioptrio, r=5
Índices de refracción, n1=1 (aire) n2=2.4 (dioptrio)
Aplicamos la ley de Snell: 1·sin θ1=2.4·sin θ2
Calculamos los ángulos
Imagen: Posición, s’=12.42, tamaño, h’=1.0
Utilizamos MATLAB para hacer los cálculos
s=-10; %posición del objeto
h=2; %tamaño del objeto
r=5; %radio del dioptrio
n1=1; %índice de refracción de aire
n2=2.4; %índice de refracción del dióptrio
alfa=atan(h/(-s+r));
theta_1=asin(h/r);
theta_2=asin(n1*sin(theta_1)/n2);
if (theta_1-theta_2)>alfa
sp=r*(-tan(alfa)+sin(theta_1)+tan(theta_1-theta_2)*(1-cos(theta_1)))
/(tan(theta_1-theta_2)-tan(alfa));
hp=(-sp+r)*tan(alfa);
fprintf('Posición %2.2f y altura %2.2f de la imagen\n',sp,hp)
else
disp('Imagen virtual')
end
Posición 12.42 y altura -0.99 de la imagen
Aproximación paraxial
Hemos estudiado la refracción de los rayos cuando inciden en una superficie de separación plana que separa dos medios de índices de refracción n1 y n2.
Supongamos ahora que la superficie de separación entre los dos medios es esférica de radio r, tal como se muestra en la figura.
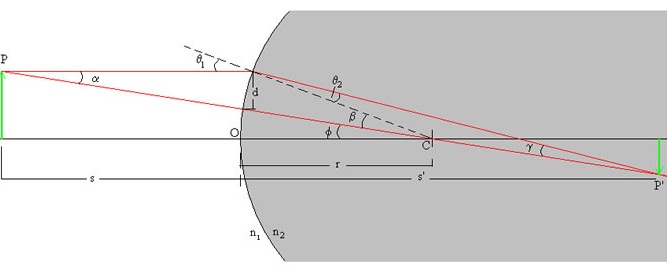
Del punto objeto P salen dos rayos de luz (en color rojo), uno paralelo al eje y otro que pasa por el centro C de la superficie esférica. La intersección de dichos rayos da lugar al punto P’ imagen de P.
Sea s la distancia de P a la superficie de separación, vamos a calcular la posición s’ de la imagen P’
Para el rayo paralelo al eje. Aplicamos la ley de Snell
Utilizando la aproximación de ángulos pequeños
En la figura vemos que:
β=γ+θ2= γ+(n1/n2) θ1
θ1=α+β
Despejando θ1 en la primera ecuación y sustituyéndola en la segunda, obtenemos
n1·α+ n2·γ=( n2- n1)·β
Utilizando las aproximaciones
Consideramos d un pequeño arco de radio r y ángulo de apertura β, por lo que, d=r·β. Llegamos a la ecuación
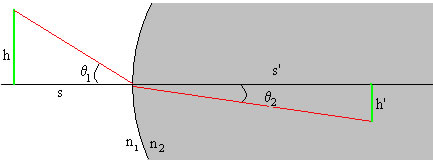
Se define aumento m como el cociente entre el tamaño de la imagen h’ y la del objeto h.
m=h’/h
Aplicando la ley de Snell
Utilizando la aproximación de ángulos pequeños
Llegamos a la expresión para el aumento m
Lentes delgadas
Aplicamos la ecuación de la aproximación paraxial de una superficie convexa a una lente delgada de índice de refracción n formada por dos superficies esféricas de radios r1 y r2, y de centros C1 y C2, tal como se muestra en la figura.
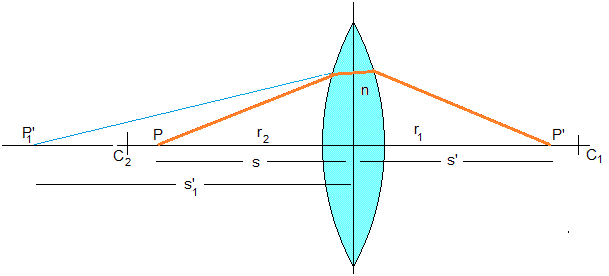
Si un objeto P está a una distancia s de la primera superficie de radio r1 y centro C1, determinamos la distancia s'1 de la imagen debida a la refracción al atravesar esta superficie.
El primer medio es el aire n1=1 y el segundo es el vidrio n2=n
Esta imagen no llega a formarse por que la luz se refracta en la segunda superficie esférica de centro C2 y radio r2. La imagen P´1 del primer dióptrio es el objeto del segundo. La distancia de este objeto para el segundo dióptrio es s2=-s'1. La imagen P’ de este objeto es
El primer medio es el vidrio n1=n y el segundo es el aire n2=1. Sumando ambas ecuaciones:
Se denomina distancia focal f de una lente delgada a la distancia imagen s' que corresponde a una distancia objeto infinita s=∞
Denominada ecuación del constructor de lentes.
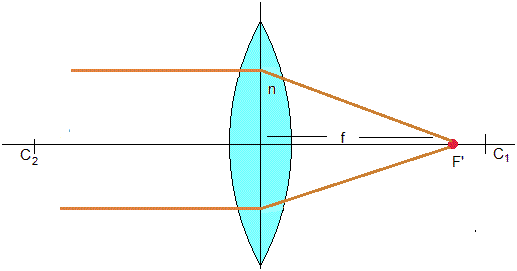
Una lente biconvexa de vidrio de n=1.46 tiene sus radios de curvatura de r1=10 cm y r2=12 cm. Hallar su distancia focal f
El radio r1 es positivo ya que el centro C1 está a la derecha de la lente. Sin embargo, el radio r2 es negativo ya que el centro del segundo dióptrio C2 está a la izquierda
f=11.86 cm
Práctica de laboratorio
El propósito de este experimento es determinar la distancia focal f de una lente delgada. En la figura se muestra cómo se forma la imagen hi de un objeto h0, mediante la intersección de dos rayos uno que pasa por el centro de la lente (no se desvía) y otro parelelo al eje que pasa por el foco F
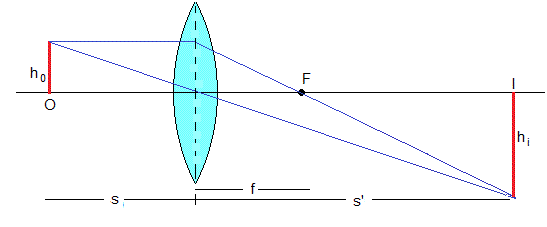
Donde f es la distancia focal, s es la distancia entre el objeto y la lente y s' es la distancia entre la imagen y la lente. Midiendo s y s' se puede determinar la distancia focal f.
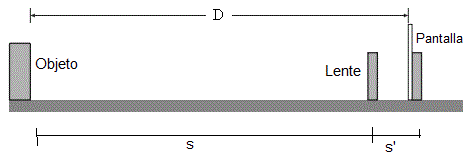
- Se coloca la fuente de luz y la pantalla tal como se muestra en la figura a una distancia D una de la otra
- Se mueve la lente hasta que se vea una imagen nítida en la pantalla. Se anota s y s'
- Sin cambiar la posición de la fuente de luz o de la pantalla, se mueve la lente a otra posición hasta conseguir una imagen nítida en la pantalla. Se anonota s y s'
| Separación, D | Distancia objeto-lente, s | Distancia lente-pantalla, s' |
|---|---|---|
| 100 | 12.3 | 87.7 |
| 100 | 87.7 | 12.3 |
| 90 | 12.6 | 77.4 |
| 90 | 77.4 | 12.6 |
| 80 | 13 | 67 |
| 80 | 67 | 13 |
| 70 | 13.5 | 56.5 |
| 70 | 56.5 | 13.5 |
| 60 | 14.3 | 45.7 |
| 60 | 45.7 | 14.3 |
| 50 | 15.8 | 34.2 |
| 50 | 34.2 | 15.8 |
x=[12.3,12.6,13,13.5,14.3,15.8];
y=[87.7,77.4,67,56.5,45.7,34.2];
xx=1./[x,y];
yy=1./[y,x];
plot(xx,yy,'ro','markersize',4,'markerfacecolor','r')
grid on
xlim([0,0.1])
ylim([0,0.1])
xlabel('1/d_0')
ylabel('1/d_i')
title('Distancia focal')
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste. El coeficiente p1=-09992.
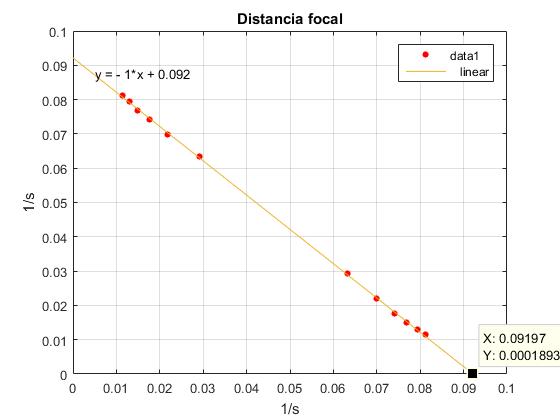
Como cabía esperar una recta de pendiente -1. Medimos la intersección de la recta con el eje X o con el eje Y, que nos da la inversa de la distancia focal f=1/0.09197=10.87 cm. El fabricante PASCO ha marcado la lente con una distancia focal f=10 cm
Distancia focal efectiva de un sistema de dos lentes
En la figura, se muestra dos lentes L1 de distancia focal f1 y L2 de distancia focal f2, separadas por una distancia d. Un rayo paralelo al eje X converge en I2 a una distancia x de la lente L2
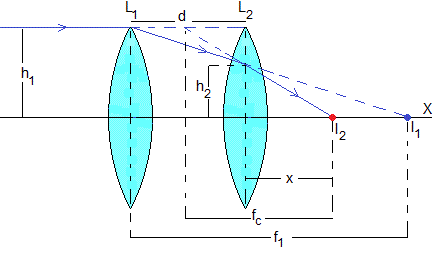
Sin la lente L2 los rayos convergerían en I1 a una distancia f1 de la primera lente.
Cuando la lente L2 está presente, I1 es el objeto para dicha la lente a una distancia s=-(f1-d), el signo - indica que I1 está detrás de L2, I2 es la imagen situada a s'=x. La ecuación de la lente delgada es
x es la distancia entre la segunda lente L2 y el foco del sistema de dos lentes
En los dos triángulos que forman los rayos y sus prolongaciones establecemos las siguientes relaciones
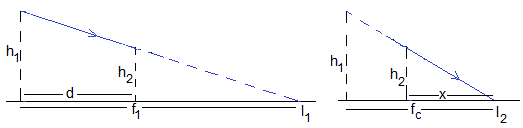
Eliminando h1/h2
Sustituyendo x
Ejemplo
Sean dos lentes: L1 cuya distancia focal es f1=0.5 m, y L2 con f2=1.00 m. La distancia entre las dos lentes d se puede modificar de 0.05 a 0.45 m. Medimos los valores de la distancia x entre la segunda lente y el foco del sistema y calculamos los valores de la distancia focal fc mediante la relación
Representamos 1/fc en función de d. La recta que mejor ajusta tendrá una pendiente próxima a -1/(f1·f2)=-2 y una ordenada en el origen, 1/f1+1/f2=3
| Separación, d | Distancia lente-foco, x |
|---|---|
| 0.050 | 0.309 |
| 0.100 | 0.284 |
| 0.150 | 0.258 |
| 0.200 | 0.229 |
| 0.250 | 0.197 |
| 0.300 | 0.164 |
| 0.350 | 0.128 |
| 0.400 | 0.093 |
| 0.450 | 0.048 |
f1=0.5;
f2=1.00;
d=0.050:0.050:0.450;
x=[0.309,0.284,0.258,0.229,0.197,0.164,0.128,0.093,0.048];
fc=f1*x./(f1-d);
plot(d,1./fc,'ro','markersize',4,'markerfacecolor','r')
grid on
xlabel('d (m)')
ylabel('1/f_c (m^-1)')
tile('Distancia focal f_c')
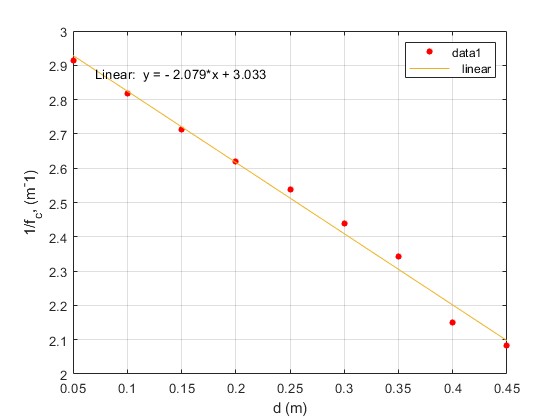
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Types of fit.
La pendiente de la recta que mejor ajusta es -2.079 y la ordenada en el origen 3.033
Referencias
Pattarapon Tanalikhit. Effective Focal Length of a Two-Lens System. The Physics Teacher, Vol. 63, October 2025, pp. 602-603

