El prisma de vidrio

El siguiente programa simula un prisma. Se puede cambiar el ángulo del prisma en el control titulado Angulo prisma y el ángulo incidente en el control Angulo incidente a continuación, se pulsa el botón titulado Nuevo
Geometría del prisma
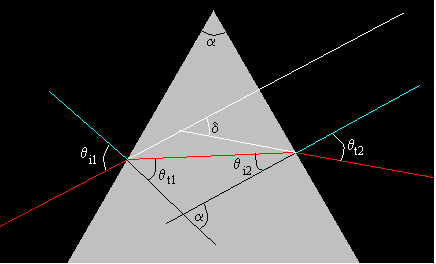
En al figura, se muestra un prisma de ángulo α hecho de un vidrio que tiene un índice de refracción n. Un rayo de luz de color rojo incide sobre la cara izquierda del prisma. El ángulo que forma el rayo incidente con la normal es θi1. Aplicamos la ley de Snell para trazar el rayo refractado
sinθi1=n·sin θt1.
θt1 es el ángulo que forma el rayo refractado con la normal a la cara izquierda del prisma. El rayo se ha desviado (θi1- θt1)
El rayo refractado llega a la cara derecha del prisma formado un ángulo θi2 con la normal. Aplicamos la ley de Snell para obtener la dirección del rayo refractado
n·sinθi2=sin θt2.
El rayo se ha desviado (θt2- θi2)
El ángulo que forma la prolongación del rayo incidente con el rayo que sale del prisma se denomina ángulo de desviación.
δ=(θi1- θt1)+ (θt2- θi2)= θi1+ θt2-α
ya que α= θt1+ θi2
Ejemplo
Sea el ángulo del prisma α=60°, y el color de la luz roja λ=640 nm o bien, el índice de refracción del prisma n=1.509 (véase en la parte superior del programa interactivo, más abajo).
El ángulo incidente θi1=30°
Aplicamos la ley de Snell en la primera superficie
Aplicamos la ley de Snell en esta superficie
Cambiamos el ángulo incidente, θi1=20°
Aplicamos la ley de Snell en la primera superficie
Aplicamos la ley de Snell en esta superficie
1·sinθi1=n·sinθt1. El ángulo de refracción es θt1=19.35°.
El rayo incide en la segunda superficie con un ángulo θi2=α-θt1=60-19.35=40.65°.
n·sinθi2=1·sinθt2. El ángulo de refracción es θt2=79.42°
El ángulo de desviación es δ= θi1+ θt2-α=30+79.42-60=49.42°, tal como comprobamos en el programa interactivo más abajo
1·sinθi1=n·sinθt1. El ángulo de refracción es θt1=13.10°.
El rayo incide en la segunda superficie con un ángulo θi2=α-θt1=60-13.10=46.90°.
n·sinθi2=1·sinθt2. El primer miembro es mayor que la unidad, por lo que no hay rayo refractado, se produce una reflexión en dicha superficie, tal como podemos apreciar en el programa interactivo
El ángulo de incidencia es igual al ángulo del prisma
Cuando el ángulo de incidencia θi1 es igual al ángulo del prisma α
Aplicamos la ley de Snell en esta superficie
Aplicamos la ley de Snell en esta superficie
1·sinα=n·sinθt1
El rayo incide en la segunda superficie con un ángulo θi2=α-θt1.
n·sinθi2=1·sinθt2.
El ángulo de desviación es δ=α+θt2-α=θt2
El en sistema de ecuaciones
eliminamos θi2 y despejamos el índice de refracción n
Ejemplo
Un recipiente en forma de prisma de ángulo α=60°, se llena de líquido de índice de refracción n desconocido. Un haz de luz proveniente de una lámpara de sodio incide con ángulo θ1i=α, se mide al ángulo de desviación δ. Los resultados son
| Líquido | Desviación, δ | Indice de refracción, n |
|---|---|---|
| Glicerina | 37° | 1.47 |
| Agua | 27° | 1.34 |
| Alcohol etílico | 28° | 1.35 |
| Benceno | 39° | 1.50 |
alfa=pi/3; %ángulo del prisma, ángulo incidente, 60º for delta=[37, 27, 28, 39]*pi/180 n=sqrt(1+sin(delta)^2/sin(alfa)^2+2*sin(delta)/tan(alfa)); disp(n) end
1.4757
1.3413
1.3550
1.5016
Reflexión total
Calculamos el ángulo de incidencia θi1 en la primera superficie, que hace que al ángulo de refracción en la segunda, θt2=π/2 (90°)
Despejamos el ángulo de incidencia, θi1
Por ejemplo, para un prisma de ángulo α=60°, e índice de refracción n=1.509, obtenemos, θi1=28.6°. Comprobamos en el programa interactivo, más abajo, que para un ángulo menor que 28.6°, se produce reflexión total para un rayo de luz de color rojo
En una experiencia de laboratorio, se puede medir el ángulo de iniciencia θi1 para obtener el índice de refracción n del prisma de ángulo α
Mínima desviación
Escribimos el ángulo de desviación δ en términos del ángulo de incidencia θi1, del índice de refracción n y del ángulo del prisma α. Después de hacer algunas operaciones llegamos a la expresión
En la figura, se representa el ángulo de desviación δ en función del ángulo de incidencia θi1.
alfa=60*pi/180; %ángulo del prisma
n=1.5; %indice de refracción
theta=(30:80)*pi/180; %ángulos de incidencia
delta=theta+asin(sin(alfa)*sqrt(n^2-sin(theta).^2)
-sin(theta)*cos(alfa))-alfa;
plot(theta*180/pi,delta*180/pi)
xlabel('\theta')
ylabel('\delta')
title('ángulo de desviación')
grid on
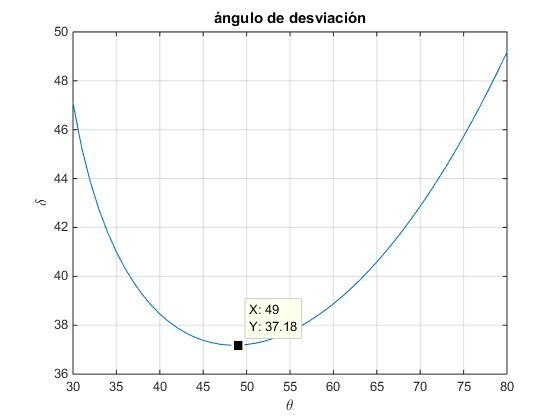
El ángulo de desviación presenta un mínimo δm para un cierto valor del ángulo de incidencia θi1. El mínimo se calcula igualando la derivada de δ respecto de θi1, a cero
Derivando la expresión anterior obtenemos una expresión muy larga, difícil de simplificar. Vamos a calcular la desviación mínima de otra forma, tal como se describe en el libro citado en las referencias. Como
De la aplicación de la ley de Snell a ambas caras del prisma tenemos las siguientes relaciones:
sinθi1=n·sin θt1.
cosθi1·dθi1=n·cos θt1·dθt1
n·sinθi2=sin θt2.
n·cosθi2·dθi2=cos θt2·dθt2
Como α= θt1+ θi2
dθt1=- dθi2
Combinando estas expresiones, obtenemos
Finalmente, de la condición de mínimo
Aplicando la ley de Snell
Como n≠1, la relación anterior es cierta para θi1=θt2 por lo que θi2=θt1
Cuando la desviación δ es mínima, el rayo atraviesa el prisma horizontalmente, tal como se muestra en la figura.
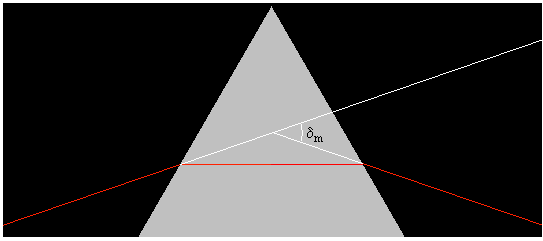
Como α= θt1+ θi2 y δ=θi1+ θt2-α
Aplicando la ley de Snell
El ángulo de incidencia θi1 para el cual se produce la desviación mínima es
Midiendo el ángulo de desviación mínima δm obtenemos el índice de refracción de la sustancia transparente. Para medir el índice de refracción de líquidos o gases se construye un prisma hueco cuyos lados son vidrios planos-paralelos, el hueco se llena con el líquido o con el gas a presión.
Ejemplo:
- Medimos el ángulo de desviación δ para calcular el índice de refracción del prisma n.
- Angulo del prisma, α=60º
- Angulo de incidencia, θi1=40º
Ángulo de desviación para la luz roja λ=640 nm, δ=39.44º
- Medimos el ángulo de desviación mínima δm para calcular el índice de refracción del prisma n.
- Angulo de incidencia, θi1=49º.
Ángulo de desviación mínima, δm=37.98º
Cambiamos el ángulo de incidencia grado a grado hasta encontrar la desviación mínima.
Comprobamos que el programa interactivo proporciona un valor correcto de la desviación mínima
Calculamos el índice de refracción
Actividades
Se introduce
- El ángulo del prisma α, en el control titulado Angulo prisma.
- El ángulo incidente θi1, en el control titulado Angulo incidente.
- Se selecciona la longitud de onda de la luz en el control titulado Longitud onda.
Se pulsa el botón titulado Nuevo
Se proporciona el dato del índice de refracción n para cada longitud de onda λ (véase el apartado titulado 'Indice de refracción') y el programa dibuja y calcula la desviación δ del rayo incidente al refractarse en la segunda superficie del prisma. Se dibujan con líneas a trazos de color azul claro, las normales a las dos superficies del prisma
Indice de refracción
El índice de refracción n no es constante, sino que depende de la longitud de onda o de la frecuencia de la luz con la que se ilumina el prisma.
Por ejemplo, el índice de refracción del vidrio denominado Borosilicate Crown para las longitudes de onda del espectro visible, se proporcionan en la siguiente tabla.
| Color | Longitud de onda nm | Indice de refracción |
|---|---|---|
| Rojo | 640 | 1.50917 |
| Amarillo | 589 | 1.51124 |
| Verde | 509 | 1.51534 |
| Azul | 486 | 1.51690 |
| Violeta | 434 | 1.52136 |
Fuente: hypertextbook.com/facts/2005/JustinChe.shtml (junio 2008)
Ajuste a un polinomio de grado m
Para calcular el índice de refracción para cualquier otra longitud de onda del espectro visible se ajusta los datos de la tabla mediante el procedimiento de los mínimos cuadrados a un polinomio de grado m.
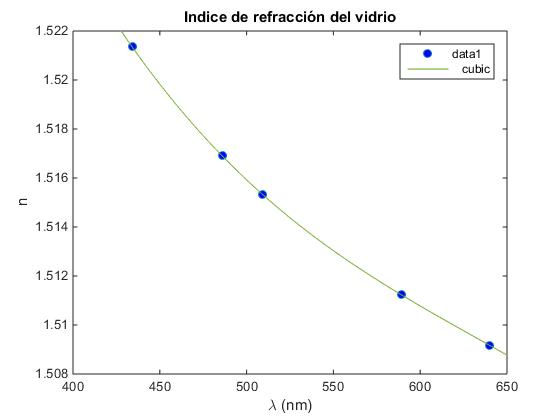
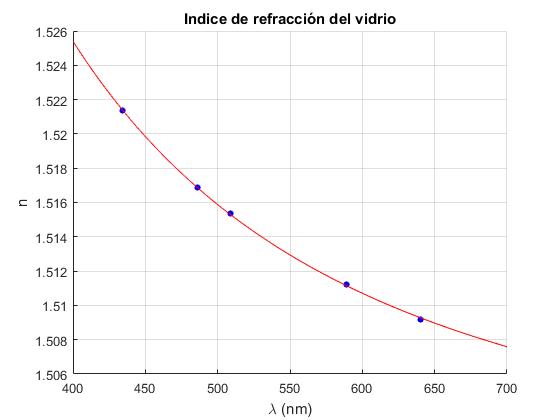
Creamos un script para representar mediante puntos la tabla de datos, en el eje X la longitud de onda en nm, en el eje Y el índice de refracción del vidrio
x=[640,589,509,486,434]; %longitud de onda en nm
y=[1.50917,1.51124,1.51534,1.51690,1.52136]; %índice de refracción
plot(x,y,'o','markersize',6,'markerfacecolor','b')
xlabel('\lambda (nm)')
ylabel('n')
title('Indice de refracción del vidrio')
Seleccionamos en el menú de la ventana gráfica que aparece Tools/Basic fitting. Probamos primero el ajuste lineal (linear), luego el ajuste a un polinomio de grado dos (quadratic), a un polinomio de grado tres (cubic). Observamos que este último ajuste parece el más conveniente. Anotamos los coeficientes del polinomio y=p1x3+p2x2+p3x+p4
p1=-5.1283·10-10, p2=9.7277·10-7, p3=-0.00065484, p4=1.6643
Ajuste no lineal
Tomando como modelo la fórmula de Cauchy para los índices de refracción del agua en la región visible del espectro, probamos un ajuste no lineal a la función
x=[640,589,509,486,434]; %longitud de onda en nm
%índice de refracción del vidrio
y=[1.50917,1.51124,1.51534,1.51690,1.52136];
hold on
plot(x,y,'bo','markersize',4,'markerfacecolor','b')
f_ajuste =@(a,x) a(1)+a(2)./x.^2;
a0=[1.3 3000]; %valor inicial de los parámetros
af=nlinfit(x,y,f_ajuste,a0);
%representa la función
g=@(x) f_ajuste(af,x);
fplot(g,[400,700],'r')
hold off
xlabel('\lambda (nm)')
ylabel('n')
title('Indice de refracción del vidrio')
>> af= 1.4990 4.2318e+03
Dos prismas pegados
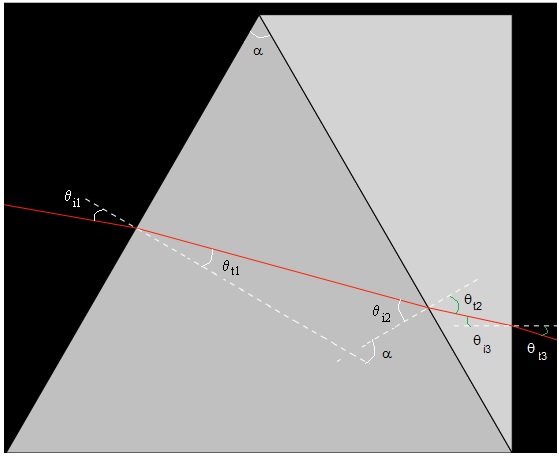
Consideremos un prisma de ángulo α pegado a medio prisma invertido tal como se muestra en la figura.
El índice de refracción del primer prisma es
El índice de refracción del segundo prisma es
con a1=1.1 y b1=1·105 nm2, la longitud de onda λ se expresa en 10-9 m
con a2=1.3 y b2=5·104 nm2
Para una determinada longitud de onda λ0 los índices de refracción de los prismas son iguales n1=n2. Un rayo pasa de un prisma al otro sin desviarse, cualquiera que sea el ángulo de incidencia θi1.
Con los datos de a1, b1, a2 y b2, λ0=500 nm. Los índice de refracción de ambos prismas valen, n1=1.5 y n2=1.5.
Trazado de los rayos
Consideremos un prisma de α=60° sobre el que incide un rayo con un ángulo θi1=40°.
Seleccionamos el color de la luz, la longitud de onda es λ=640 nm, (rojo)
Seleccionamos el color de la luz, la longitud de onda es λ=434 nm, (violeta)
Seleccionamos el color de la luz, la longitud de onda es λ=500 nm, (verde)
Los índices de refracción valen: n1=1.344, y n2=1.422.
Aplicamos la ley de Snell en la primera superficie, 1·sinθi1=n1·sinθt1. El ángulo de refracción es θt1=28.57°.
El rayo incide en la superficie de separación con un ángulo θi2=α-θt1=60-28.57=31.43°. Aplicamos la ley de Snell en esta superficie, n1·sinθi2=n2·sinθt2. El ángulo de refracción es θt2=29.53°
El ángulo de incidencia en la superficie vertical, es θi3=α/2-θt2=0.47°. Aplicamos la ley de Snell en esta superficie, n2·sinθi3=1·sinθt3, se obtiene θt3=0.67°, que es el valor que nos proporciona el programa interactivo en la esquina superior derecha.
Los índices de refracción valen: n1=1.631, y n2=1.565.
Aplicamos la ley de Snell en la primera superficie, 1·sinθi1=n1·sinθt1. El ángulo de refracción es θt1=23.21°.
El rayo incide en la superficie de separación con un ángulo θi2=α-θt1=60-23.21=36.79°. Aplicamos la ley de Snell en esta superficie, n1·sinθi2=n2·sinθt2. El ángulo de refracción es θt2=38.60°
El ángulo de incidencia en la superficie vertical, es θi3=α/2-θt2=-8.60°. Aplicamos la ley de Snell en esta superficie, n2·sinθi3=1·sinθt3, se obtiene θt3=-13.54°, que es el valor que nos proporciona el programa interactivo en la esquina superior derecha.
Los índices de refracción valen: n1=1.5, y n2=1.5.
Aplicamos la ley de Snell en la primera superficie, 1·sinθi1=n1·sinθt1. El ángulo de refracción es θt1=25.37°.
El rayo se propaga sin desviación hasta la superficie vertical
El ángulo de incidencia en la superficie vertical, es θi3=α/2-θt1=4.63°. Aplicamos la ley de Snell en esta superficie, n2·sinθi3=1·sinθt3, se obtiene θt3=6.95°, que es el valor que nos proporciona el programa interactivo en la esquina superior derecha.
Un rayo incidente horizontal produce un rayo emergente horizontal
Para que el rayo incidente sea horizontal, el ángulo de incidencia en la primera superficie será θi1=α/2. Para que el rayo emergente del prisma que incide sobre la superficie vertical sea horizontal θt2=α/2.
Aplicamos la ley de Snell en la primera superficie, 1·sinθi1=n1·sinθt1
Aplicamos la ley de Snell en la superficie de separación, n1·sinθi2=n2·sinθt2
Tenemos un sistema de dos ecuaciones
Eliminamos la incógnita θt1
Obtenemos la ecuación bicuadrada, en λ
Sea el ángulo del prisma, α=60°, la ecuación que tenemos que resolver es
Con los datos dados al principio de este apartado, obtenemos, λ=1178.3 nm. Un rayo que incide con ángulo 30°, sale horizontal del prisma, el ángulo θt3=0°, que es el valor que nos proporciona el programa interactivo en la esquina superior derecha.
Actividades
Se introduce
- El ángulo del prisma α, en el control titulado Angulo prisma.
- El ángulo incidente θi1, en el control titulado Angulo incidente.
- Se selecciona la longitud de onda de la luz en el control titulado Longitud onda.
Se pulsa el botón titulado Nuevo
Fijamos la longitud de onda y cambiamos el ángulo de incidencia, hasta encontrar el valor de la desviación mínima. A partir de este dato, calculamos el índice de refracción.
Referencias
Hetch-Zajac. Optica. Addison-Wesley Iberoamericana (1986), págs. 138-139
B. P. Chandra, S. C. Bhaiya. A simple, accurrate alternative to the minimum deviation method of determining the refactive index of liquids. Am. J. Phys. 51 (2) February 1983, pp. 160-161
Edward Richard Van Keuren. Refractive index measurement using total internal reflection. Am. J. Phys. 73 (7) July 2005, pp. 611-614
International Physics Olympiad. Theoretical Question III. Romania, 1983

