En la figura vemos el observador a la derecha, el objeto a la izquierda y su imagen invertida

Variación del índice de refracción con la altura

El índice de refracción de aire depende de su densidad, la densidad depende de la temperatura y la presión que podemos considerar constante hasta una altura considerable.

A alta temperatura, cerca de la superficie caliente, el aire es menos denso y el índice de refracción es más pequeño.

La temperatura por encima del suelo caliente disminuye rápidamente con la altura hasta que se estabiliza a una altura del orden de un metro. Se considera que el índice de refracción sigue un comportamiento descrito por la función

${\displaystyle n^2(y)=n_0^2+n_1^2\left(1-\exp (-\alpha y)\right)}$

donde y es la altura por encima del suelo y n₀, n₁ y α son constantes que describen un determinado perfil del índice de refracción del aire por encima de la superficie caliente.

En la figura, se representa esta función para n₀=1.000233, n₁=0.4584, α=2.3003 m^-1, (véase el artículo citado en las referencias)

n0=1.000233;
n1=0.4584;
alfa=2.3003;
f=@(y) sqrt(n0^2+n1^2*(1-exp(-alfa*y)));
fplot(f,[0.01,3])
grid on
%ylim([1,1.15])
xlabel('y')
ylabel('n')
title('Indice de refracción')

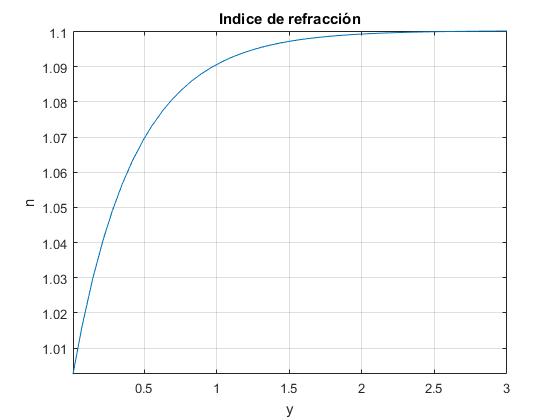
El índice de refracción tiende hacia un valor constante, cuando y se hace grande

>> sqrt(n0^2+n1^2)
ans =    1.1003

Ecuación del camino que sigue la luz

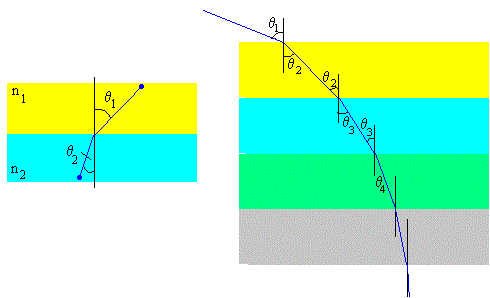
Cuando un rayo de luz atraviesa la superficie de separación de dos medios de distinto índice de refracción se cumple la ley de Snell de la refracción

n₁·sinθ₁=n₂·sinθ₂

siendo n₁ y n₂ los índices de refracción de los dos medios, θ₁ es el ángulo de incidencia y θ₂ el ángulo de refracción.

Cuando un rayo de luz atraviesa un medio estratificado consistente en capas de índices de refracción n₁, n₂, n₃…. se cumple que n₁·sinθ₁=n₂·sinθ₂
n₂·sinθ₂=n₃·sinθ₃
n₃·sinθ₃=n₄·sinθ₄
……

Si el índice de refracción n varía de forma continua con la altura y, tendremos que

n(y)·sinθ=c

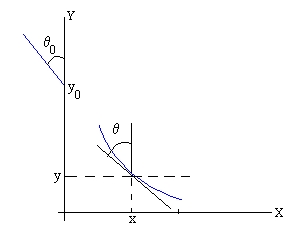
donde c es una constante que se determina a partir de los datos del índice de refracción a la altura y₀, y el ángulo θ₀ que forma el rayo con el eje vertical Y.

n(y₀)·sinθ₀=c

Al variar el índice de refracción el rayo de luz describe una curva, la pendiente de la recta tangente dy/dx a dicha curva en el punto (x, y) es

${\displaystyle \frac{dy}{dx}=-\frac{1}{\tan \theta }}$

Como vemos en la figura, el ángulo que forma la tangente al rayo de luz en el punto (x, y) es 90+θ

${\displaystyle \frac{dy}{dx}=-\frac{\sqrt{1-{\sin }^2\theta }}{\text{sin}\theta }=-\frac{\sqrt{1-c^2/n^2(y)}}{c/n(y)}=-\sqrt{\frac{n^2(y)}{n^2(y_0){\sin }^2{\theta }_0}-1}}$

Integramos esta ecuación diferencial sabiendo que el rayo de luz tiene su origen en el objeto situado en el punto P (0, y₀)

${\displaystyle \frac{dy}{dx}=-\sqrt{\frac{n_0^2+n_1^2-n_1^2\exp (-\alpha y)-n_P^2{\sin }^2{\theta }_0}{n_P^2{\sin }^2{\theta }_0}}}$

Se definen las constantes

${\displaystyle \begin{array}{l}{n}_P^2=n^2(y_0)=n_0^2+n_1^2\left(1-\exp (-\alpha y_0)\right)\\ k^2=\frac{n_0^2+n_1^2-n_P^2{\sin }^2{\theta }_0}{n_1^2}\\ \frac{dy}{dx}=-\frac{n_1}{n_P\sin {\theta }_0}\sqrt{k^2-\exp (-\alpha y)}\end{array}}$

Separamos variables para integrar

${\displaystyle {\displaystyle \underset{y_0}{\overset{y}{\int }}\frac{dy}{\sqrt{k^2-\exp (-\alpha y)}}}=-{\displaystyle \underset{0}{\overset{x}{\int }}\frac{n_1}{n_P\sin {\theta }_0}dx}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}{t}^2=k^2-\exp (-\alpha y)\\ y=-\frac{1}{\alpha }\ln (k^2-t^2)\\ {\displaystyle \underset{t_0}{\overset{t}{\int }}\frac{dt}{k^2-t^2}=-\frac{n_1\alpha }{2n_P\sin {\theta }_0}}x\\ \frac{1}{2k}\ln \left|\frac{k+t}{k-t}\right|-\frac{1}{2k}\ln \left|\frac{k+t_0}{k-t_0}\right|=-\frac{n_1\alpha }{2n_P\sin {\theta }_0}x\end{array}}$

Deshacemos el cambio de variable

$$\begin{gathered} {\displaystyle \begin{array}{l}\ln \left|\frac{k+\sqrt{k^2-\exp (-\alpha y)}}{k-\sqrt{k^2-\exp (-\alpha y)}}\right|=-\frac{n_{1}k\alpha }{n_P\sin {\theta }_0}x+\ln \left|\frac{k+\sqrt{k^2-\exp (-\alpha y_0)}}{k-\sqrt{k^2-\exp (-\alpha y_0)}}\right|\\ \ln \left|\frac{\exp (-\alpha y)}{{\left(k-\sqrt{k^2-\exp (-\alpha y)}\right)}^2}\right|=-\frac{n_{1}k\alpha }{n_P\sin {\theta }_0}x+\ln \left|\frac{\exp (-\alpha y_0)}{{\left(k-\sqrt{k^2-\exp (-\alpha y_0)}\right)}^2}\right|\\ \ln \left|\frac{1}{{\left(k\exp \left(\frac{1}{2}\alpha y\right)-\sqrt{{\left(k\exp \left(\frac{1}{2}\alpha y\right)\right)}^2-1}\right)}^2}\right|=-\frac{n_{1}k\alpha }{n_P\sin {\theta }_0}x+\ln \left|\frac{1}{{\left(k\exp \left(\frac{1}{2}\alpha y_0\right)-\sqrt{{\left(k\exp \left(\frac{1}{2}\alpha y_0\right)\right)}^2-1}\right)}^2}\right|\\ -2\ln \left\{k\exp \left(\frac{1}{2}\alpha y\right)-\sqrt{{\left(k\exp \left(\frac{1}{2}\alpha y\right)\right)}^2-1}\right\}= \\ -\frac{n_{1}k\alpha }{n_P\sin {\theta }_0}x-2\ln \left\{k\exp \left(\frac{1}{2}\alpha y_0\right)-\sqrt{{\left(k\exp \left(\frac{1}{2}\alpha y_0\right)\right)}^2-1}\right\}\end{array}} \end{gathered}$$

Conocida la definición de la función recíproca del coseno hiperbólico (más abajo), finalmente, la ecuación del rayo de luz queda de la siguiente forma.

${\displaystyle {\cosh }^{-1}\left(k\exp \left(\frac{\alpha y}{2}\right)\right)=-\frac{n_{1}k\alpha }{2n_P\sin {\theta }_0}x+{\cosh }^{-1}\left(k\exp \left(\frac{\alpha y_0}{2}\right)\right)}$

Para trazar el rayo de luz se da valores a x y se despeja y del siguiente modo:

${\displaystyle \begin{array}{l}{\cosh }^{-1}\left(k\exp \left(\frac{\alpha y}{2}\right)\right)=f(x)\\ k\exp \left(\frac{\alpha y}{2}\right)=\cosh \left(f(x)\right)\\ y=\frac{2}{\alpha }\ln \left\{\frac{\cosh \left(f(x)\right)}{k}\right\}\end{array}}$

Mínimo

El rayo de luz tiene un mínimo, igualando a cero la pendiente de la recta tangente dy/dx=0

${\displaystyle \begin{array}{l}\frac{dy}{dx}=-\frac{n_1}{n_P\sin {\theta }_0}\sqrt{k^2-\exp (-\alpha y)}=0\\ \exp (-\alpha y_m/2)=k\\ y_m=-\frac{2}{\alpha }\ln k\end{array}}$

La abscisa x_m vale

${\displaystyle \begin{array}{l}{\cosh }^{-1}\left(k\exp \left(\frac{\alpha y_m}{2}\right)\right)=-\frac{n_1\alpha k}{2n_P\sin {\theta }_0}{x}_m+{\cosh }^{-1}\left(k\exp \left(\frac{\alpha y_0}{2}\right)\right)\\ {\cosh }^{-1}(1)=-\frac{n_1\alpha k}{2n_P\sin {\theta }_0}{x}_m+{\cosh }^{-1}\left(k\exp \left(\frac{\alpha y_0}{2}\right)\right)\\ x_m=\frac{2n_P\sin {\theta }_0}{n_1\alpha k}{\cosh }^{-1}\left(k\exp \left(\frac{\alpha y_0}{2}\right)\right)\end{array}}$

La trayectoria que sigue la luz es simétrica respecto del mínimo

Trazamos la trayectoria que sigue la luz para y₀=3, y θ₀=80° (ángulo del rayo con la vertical)

n0=1.000233;
n1=0.4584;
alfa=2.3003;
%rayo de luz
y0=3;
angulo=80*pi/180;

np=sqrt(n0^2+n1^2*(1-exp(-alfa*y0)));
k=sqrt(n0^2+n1^2-np^2*sin(angulo)^2)/n1;
f=@(x) 2*log(cosh(-n1*alfa*k*x/(2*np*sin(angulo))+
acosh(k*exp(alfa*y0/2)))/k)/alfa;
fplot(f,[0,33])
grid on
xlabel('x')
ylabel('y')
title('Espejismo')

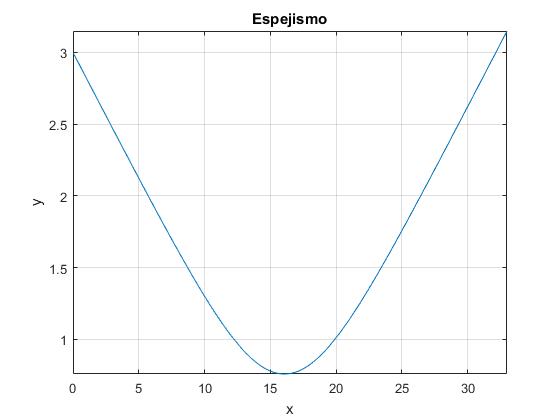
El mínimo de la trayectoria se encuentra en

>> xm=2*np*sin(angulo)*acosh(k*exp(alfa*y0/2))/(n1*alfa*k)
xm =   16.0766
>> f(xm)
ans =    0.7585

Trazamos varias trayectorias de un haz de luz, que parte de y₀=3. Las unidades en el eje X e Y ahora son iguales

n0=1.000233;
n1=0.4584;
alfa=2.3003;
%rayo de luz
y0=3;
hold on
for angulo=(80:2:90)*pi/180
    np=sqrt(n0^2+n1^2*(1-exp(-alfa*y0)));
    k=sqrt(n0^2+n1^2-np^2*sin(angulo)^2)/n1;
    f=@(x) 2*log(cosh(-n1*alfa*k*x/(2*np*sin(angulo))+
acosh(k*exp(alfa*y0/2)))/k)/alfa;
    fplot(f,[0,30])
end
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Espejismo')

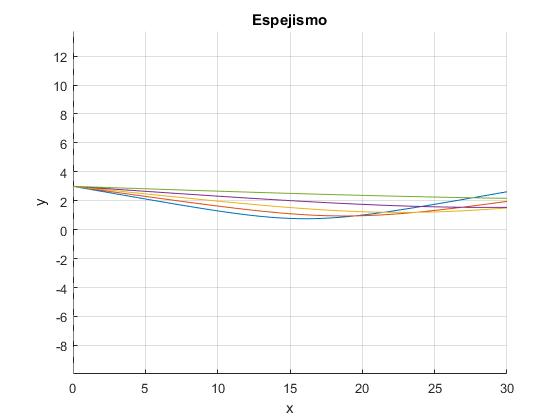
Ecuación diferencial de la trayectoria

Al final de la página titulada Propagación en un medio no homogéneo en el apartado 'El índice de refracción n varía con la altura y', obtuvimos la ecuación diferencial de la trayectoria seguida por el rayo de luz

${\displaystyle n\frac{d^{2}y}{d{x}^2}=\left(1+{\left(\frac{dy}{dx}\right)}^2\right)\frac{dn}{dy}}$

En este ejemplo, el índice de refración n depende de y de la forma

${\displaystyle n^2(y)=n_0^2+n_1^2\left(1-\exp (-\alpha y)\right)}$

La ecuación diferencial se escribe

${\displaystyle \frac{d^{2}y}{d{x}^2}=\frac{n_1^2\alpha \exp (-\alpha y)}{2\left(n_0^2+n_1^2\left(1-\exp (-\alpha y)\right)\right)}\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}$

Resolvemos la ecuación diferencial con las siguientes condiciones iniciales, para x=0, y=y₀ y (dy/dx)₀=-tan(π/2-θ₀). Fijarse que θ₀ es el ángulo que forma el rayo con la vertical, -(π/2-θ₀) es el ángulo que forma con el eje X

n0=1.000233;
n1=0.4584;
alfa=2.3003;
%rayo de luz
y0=3;
angulo=-(90-80)*pi/180;
%t es x y x es y
f=@(t,x) [x(2);n1^2*alfa*exp(-alfa*x(1))*(1+x(2)^2)/
(2*(n0^2+n1^2*(1-exp(-alfa*x(1)))))];
[t,x]=ode45(f,[0,30],[y0,tan(angulo)]); 
plot(t,x(:,1))
grid on
xlabel('x')
ylabel('y')
title('Espejismo')

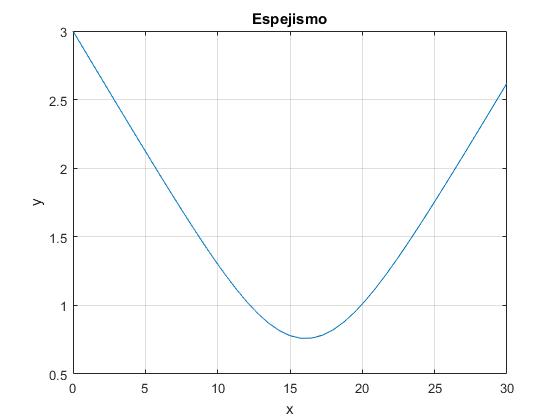
Como podemos apreciar, la integración numérica conduce a resultados similares a los de la solución analítica

Imagen virtual. Espejismo

Cuando el observador se encuentra en una posición tal como A, recibirá la luz directamente del objeto y también de los rayos que se han refractado hacia arriba debido a cambio brusco del índice de refracción cerca de la superficie caliente. El observador verá una imagen virtual P’ del objeto P y también verá el objeto P.  La imagen virtual aparecerá distorsionada ya que la prolongación de los rayos no converge en un punto.

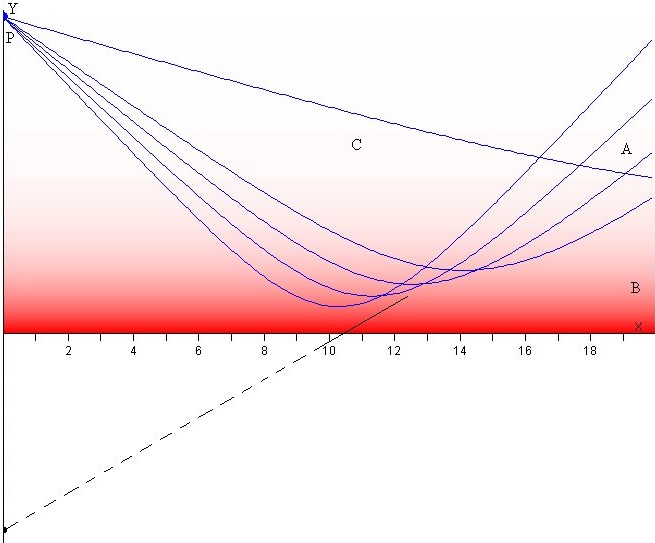
Dependiendo de la altura del objeto, el observador no verá la imagen virtual, el espejismo, si está a cierta distancia del objeto, por ejemplo en C, pero podrá ver el objeto directamente.

A partir de cierta distancia, el observador no verá ni el objeto ni su imagen virtual, por ejemplo en B.

Actividades

Se introduce

• La altura y₀ del objeto en cm, en el control titulado Altura

• El ángulo θ₀ que forma el rayo incidente con el eje Y, en la posición y₀ del objeto, en el control titulado Ángulo.

Se pulsa el botón titulado Nuevo.

Se representa el gradiente de temperaturas en tonalidades rojas. Rojo intenso cerca de la superficie que rápidamente tiende hacia el blanco. La densidad y

Se cambia el ángulo θ₀ y se vuelve a pulsar el botón titulado Ángulo

Se traza otro rayo

Cuando se hayan trazado varios rayos, se cambia la altura y₀ del objeto y el ángulo θ₀ y se pulsa el botón titulado Nuevo.

Se sugiere al lector, que para una altura y₀ del objeto, identifique de forma cualitativa las posiciones del observador en las que puede ver:

• El objeto directamente y su imagen virtual
• Solamente la imagen virtual
• Solamente el objeto
• Ni el objeto ni la imagen virtual (región de sombra)

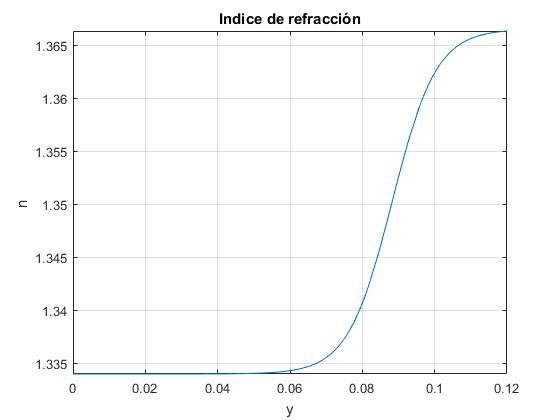
Soluciones acuosas

En una mezcla de azucar y agua el índice de refracción n varía con la altura y de la forma

${\displaystyle n=n_0+\frac{c}{1+d\exp (\alpha y)}}$

Los valores de los parámetros de ajuste a los datos experimentales son: n₀=1.334, c=0.03650, d=1.964·10⁶, α=-164.2

n0=1.334;
c=0.03250;
d=1.964e6;
alfa=-164.2;
f=@(y) n0+c./(1+d*exp(alfa*y));
fplot(f,[0,0.12])
grid on
xlabel('y')
ylabel('n')
title('Indice de refracción')

Trazamos rayos con ángulo -5° desde las posiciones y₀ comprendidas entre; 0.06 y 0.12.

n0=1.334;
c=0.03250;
d=1.964e6;
alfa=-164.2;
%rayo de luz
f=@(t,x) [x(2); -c*alfa*d*exp(alfa*x(1))*(1+x(2)^2)/((n0*(1+d*exp(alfa*x(1)))+c)*
(1+d*exp(alfa*x(1))))];
hold on
angulo=-5*pi/180;
for y0=0.06:0.005:0.12
%t es x y x es y
    [t,x]=ode45(f,[0,0.5],[y0,tan(angulo)]); 
    plot(t,x(:,1))
end
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('Espejismo')

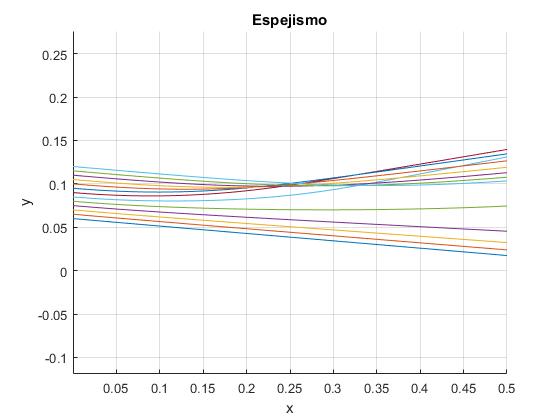
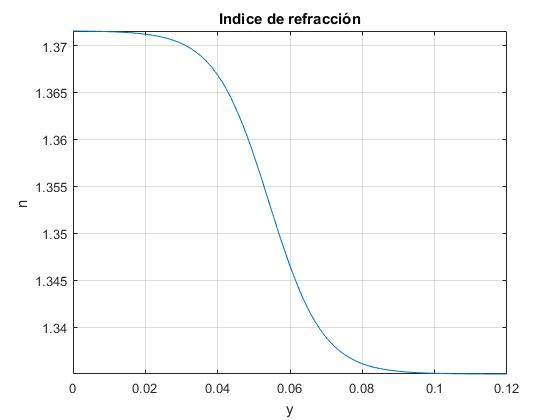
En una mezcla de alcohol y agua el índice de refracción n varía con la altura y de la misma forma funcional. Los valores de los parámetros de ajuste a los datos experimentales son: n₀=1.335, c=0.03657, d=6.778·10^-4, α=134.6

n0=1.335;
c=0.03657;
d=6.778e-4;
alfa=134.6;
f=@(y) n0+c./(1+d*exp(alfa*y));
fplot(f,[0,0.12])
grid on
xlabel('y')
ylabel('n')
title('Indice de refracción')

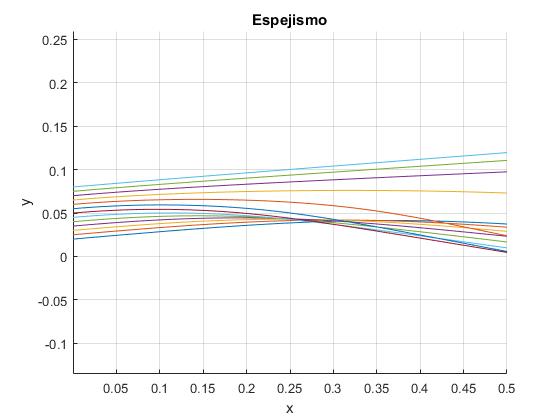
Trazamos rayos con un ángulo de 5° desde las posiciones y₀ comprendidas entre; 0.02 y 0.08.

n0=1.335;
c=0.03657;
d=6.778e-4;
alfa=134.6;
%rayo de luz
f=@(t,x) [x(2); -c*alfa*d*exp(alfa*x(1))*(1+x(2)^2)/((n0*(1+d*exp(alfa*x(1)))+c)
*(1+d*exp(alfa*x(1))))];
hold on
angulo=5*pi/180;
for y0=0.02:0.005:0.08
%t es x y x es y
    [t,x]=ode45(f,[0,0.5],[y0,tan(angulo)]); 
    plot(t,x(:,1))
end
hold off
grid on
axis equal
xlabel('x')
ylabel('y')
title('Espejismo')

En el segundo artículo citado en las referencias, se compara la imagen real y la que ve el observador

Referencias

Khular E., Thyagarajan K., Ghatak A. K., A note on mirage formation. Am. J. Phys. 45 (1) January 1977, pp. 90-92

T López-Arias, G Calzá, L M Gratton, S Oss. Mirages in a bottle. Physics Education, 44 (6) 2009, pp 582-588