El arco iris

El arco iris único y brillante que se ve después de un chubasco o en una cascada es el arco iris primario. Su característica principal son las bandas de colores, desde el violeta en el interior, pasando por el azul, verde, amarillo, naranja, hasta el rojo en el exterior.

Por encima del arco primario se encuentra el arco secundario, en el que los colores aparecen en orden inverso, el rojo en el interior y el violeta en el exterior. En medio de los dos arcos hay una región bastante más oscura que el cielo circundante denominada banda de Alejandro, en honor al filósofo griego Alejandro de Afrodisias, quien la describió por primera vez hacia el año 200 A. C.

Muy pocas veces son visibles los denominados arcos supernumerarios una serie de bandas débiles en las que suelen alternar el rosa y el verde, hacia la parte interna del arco primario, o en la parte exterior del arco secundario.

Vista de los arcos primario y secundario, en Durango (Vizcaya). Al fondo el monte Oiz.

Roger Bacon en 1266 midió el ángulo que forman los rayos del arco iris con la luz solar incidente. Descartes demostró que el arco iris primario está formado por los rayos que penetran en una gota refractándose, se reflejan una vez en su superficie interna y salen de la gota refractándose de nuevo. El arco iris secundario está formado por los rayos que penetran en la gota y se reflejan dos veces en su superficie interna. La figura de abajo, es la explicación de Descartes a la formación del arco primario y secundario.

En la figura de abajo, se muestra el arco primario y secundario producidos en una simulación con ordenador, no se ha tenido en cuenta que el arco iris secundario es menos intenso que el primario.

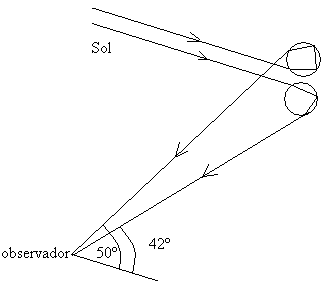
El arco primario se forma un ángulo de aproximadamente 42º y se produce después de una reflexión de los rayos de luz en el interior de la gota. En el interior del arco observamos el color violeta y en el exterior el rojo.
El arco secundario se forma un ángulo de aproximadamente 50º y se produce después de dos reflexiones de los rayos de luz en el interior de la gota. En el interior del arco observamos el color rojo y en el exterior el violeta.

Observamos también que el arco secundario tiene una anchura angular mayor que el primario. Los ángulos de desviación de la luz monocromática se calculan en los siguientes apartados

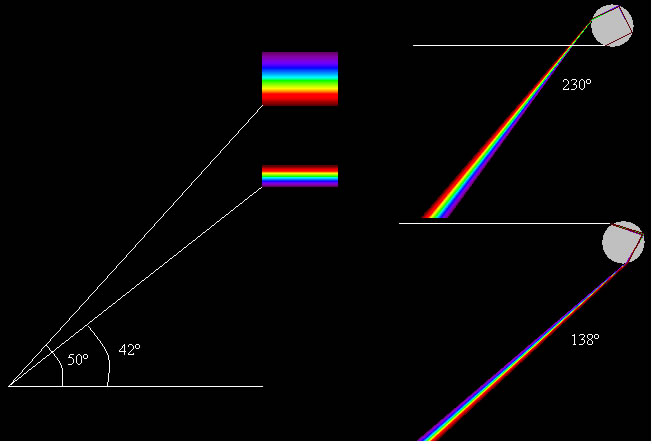
Indice de refracción

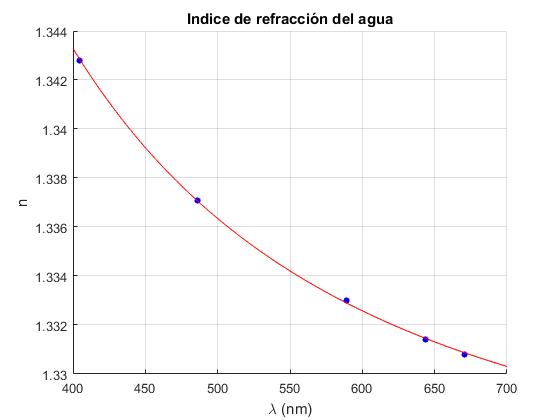
La refracción, como observó Newton con el prisma, depende del color. La luz de longitudes de onda diferentes se desvían según ángulos ligeramente distintos, esta dependencia entre el índice de refracción y la frecuencia de la luz se denomina dispersión.

Longitud de onda, nm	Indice de refracción del agua a 20º C
670.8	1.3308
643.8	1.3314
589.3	1.3330
486.4	1.3371
404.7	1.3428

Fuente: Koshkin N. I., Shirkévich M. G.. Manual de Física Elemental. Editorial Mir 1975. pág. 210

Tomando como modelo la fórmula de Cauchy para los índices de refracción del agua en la región visible del espectro, ajustamos los datos de la tabla a la función no lineal

$y = a + \frac{b}{x^{2}}$

x=[670.8,643.8,589.3,486.4,404.7];  %longitud de onda en nm
y=[1.3308,1.3314,1.3330,1.3371,1.3428]; %índice de refracción del agua
hold on
plot(x,y,'bo','markersize',4,'markerfacecolor','b')
f_ajuste =@(a,x) a(1)+a(2)./x.^2;          
a0=[1.3 3000];  %valor inicial de los parámetros
af=nlinfit(x,y,f_ajuste,a0);
%representa la función 
g=@(x) f_ajuste(af,x);
fplot(g,[400,700],'r')
hold off
xlabel('\lambda (nm)')
ylabel('n')
grid on
title('Indice de refracción del agua')

>> af =   1.0e+03 *    0.0013    3.0843

$n = 1.324 + \frac{3084.3}{λ^{2}} λ en nm$

Trayectoria de un rayo de luz monocromático

Cuando un rayo de luz incide en la superficie de una gota de forma esférica, una parte del rayo se refleja y la otra parte se transmite (1). La luz transmitida pasa al interior de la gota donde cambia de dirección debido a la refracción. Cuando llega a la superficie interna de la gota (2), una parte se refleja en su superficie y la otra parte se transmite al exterior cambiando de dirección debido a la refracción y así, sucesivamente.

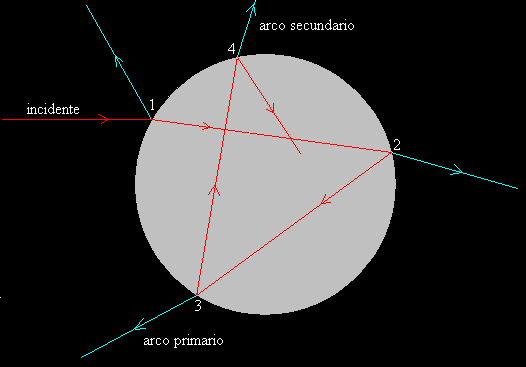
El rayo incidente forma un ángulo i con la dirección radial, se refracta acercándose a la normal, formando un ángulo r, con la dirección radial tal que

sini=n·sinr

El rayo cambia de dirección un ángulo (i-r)

Se refleja k veces en la superficie de la gota, cambiando de dirección (π-2r) en cada reflexión

Se transmite al exterior de la gota. El ángulo incidente es ahora r y el ángulo refractado forma un ángulo i con la dirección radial. El rayo cambia de dirección un ángulo (i-r)

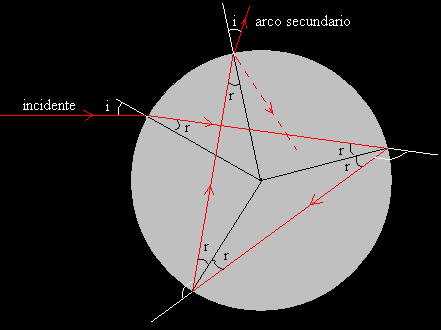
La desviación total del rayo, es

D=(i-r)+k(π-2r)+ (i-r)=kπ+2i-2(k+1)r

Donde k es el número de veces que el rayo se refleja en el interior de la gota

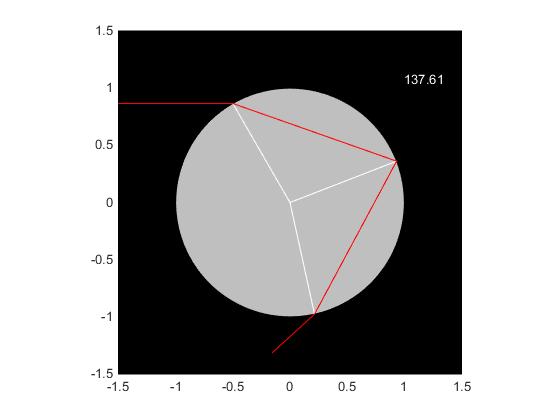
Creamos un script de MATLAB, para tazar la trayectoria de un rayo de luz de una determinada longitud de onda. Se introduce el ángulo incidente en grados, la longitud de onda en nanómetros y el número de reflexiones internas (una o dos). El programa nos proporciona el ángulo de desviación en grados en la esquina superior derecha

angulo=60;  %angulo incidente en grados
lonOnda=671; % en nm=10^-9 m
k=1; % número de reflexiones

%cálculo
n=1.324+3084.3/lonOnda^2; %índice de refracción
%dibuja la gota
R=1; % radio de la gota
ang=0:360;
x=R*sind(ang);
y=R*cosd(ang);
hold on
%marco
xx=[-3*R/2,3*R/2,3*R/2,-3*R/2];
yy=[3*R/2,3*R/2,-3*R/2,-3*R/2];
fill(xx,yy,'k')
fill(x,y,[0.75 0.75 0.75]) %gota de color gris claro, silver

%trazado de rayos
angIncidente=angulo*pi/180;
y1=R*sin(angIncidente);
x1=-R*cos(angIncidente);
line([-3*R/2,x1],[y1,y1],'color',[1 0 0]);
angRefractado=asin(sin(angIncidente)/n); %ángulo refractado
line([0 x1],[0,y1],'color','w')
for i=0:k
    m=-tan(angIncidente-angRefractado+i*(pi-2*angRefractado));
    b=y1-m*x1;
    x2=-x1-2*m*b/(m^2+1);
    y2=m*x2+b;
    line([0 x2],[0,y2],'color','w');
    line([x1,x2],[y1,y2],'color',[1 0 0]);
    x1=x2; y1=y2;
end
delta=-k*pi-2*angIncidente+2*(k+1)*angRefractado;
m=tan(delta);
b=y2-m*x2;
x2=x1+R*cos(delta)/2;
y2=y1+R*sin(delta)/2;
line([x1,x2],[y1,y2],'color',[1 0 0]);	
texto=sprintf('%3.2f\n',-delta*180/pi);
text(R,R,texto,'color','w')

axis equal
xlim([-3*R/2,3*R/2])
ylim([-3*R/2,3*R/2])
hold off

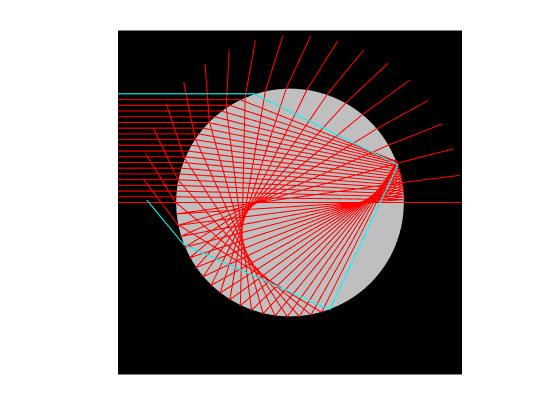
Modificamos el código del script para trazar un haz de rayos paralelos al eje horizontal de la gota. Cambiando el valor del número de reflexiones internas k=2, trazamos la trayectoria que sigue la luz de una determinada longitud de onda para formar el arco secundario

lonOnda=671; % en nm=10^-9 m
k=1; % número de reflexiones

%cálculo
n=1.324+3084.3/lonOnda^2; %índice de refracción
%dibuja la gota
R=1; % radio de la gota
ang=0:360;
x=R*sind(ang);
y=R*cosd(ang);
hold on
%marco
xx=[-3*R/2,3*R/2,3*R/2,-3*R/2];
yy=[3*R/2,3*R/2,-3*R/2,-3*R/2];
fill(xx,yy,'k')
fill(x,y,[0.75 0.75 0.75]) %gota de color gris claro, silver

%trazado de rayos paralelos al eje horizontal
for y1=0:0.05:0.95
    angIncidente=asin(y1/R);
    x1=-R*cos(angIncidente);
    line([-3*R/2,x1],[y1,y1],'color',[1 0 0]);
    angRefractado=asin(sin(angIncidente)/n); %ángulo refractado
         for i=0:k
            m=-tan(angIncidente-angRefractado+i*(pi-2*angRefractado));
            b=y1-m*x1;
            x2=-x1-2*m*b/(m^2+1);
            y2=m*x2+b;
            line([x1,x2],[y1,y2],'color',[1 0 0]);
            x1=x2; y1=y2;
        end
    delta=-k*pi-2*angIncidente+2*(k+1)*angRefractado;
    m=tan(delta);
    b=y2-m*x2;
    x2=x1+R*cos(delta)/2;
    y2=y1+R*sin(delta)/2;
    line([x1,x2],[y1,y2],'color',[1 0 0]);	
end
axis equal
axis off   %elimina los ejes
xlim([-3*R/2,3*R/2])
ylim([-3*R/2,3*R/2])
hold off

Rayo cartesiano

Fijando el número k de veces que el rayo se refleja internamente. Para distintos valores del ángulo de incidencia i obtenemos distintos valores del ángulo de desviación D.

Los arcos se forman para un ángulo de incidencia θ_c tal que el ángulo de desviación D alcanza el valor mínimo. Entonces la densidad de los rayos que dejan la gota es máxima.

$\begin{array}{l} \frac{d D}{d i} = 2 - 2 (k + 1) \frac{d r}{d i} \\ \cos i = n \cos r \frac{d r}{d i} \\ \cos r = \sqrt{1 - \sin^{2} r} = \sqrt{1 - \frac{1}{n^{2}} \sin^{2} i} = \sqrt{1 - \frac{1}{n^{2}} + \frac{1}{n^{2}} \cos^{2} i} \\ \frac{d D}{d i} = 2 - 2 (k + 1) \frac{\cos i}{\sqrt{n^{2} - 1 + \cos^{2} i}} \end{array}$

Poniendo dD/di=0, se despeja el ángulo de incidencia i.

$\cos^{2} i = \frac{n^{2} - 1}{k (k + 2)}$

Este es el ángulo de incidencia del denominado rayo cartesiano

Para determinar si las direcciones de los arcos corresponden a un máximo o a un mínimo, volvemos a derivar el ángulo de desviación D, respecto del ángulo de incidencia i.

$\frac{d^{2} D}{d i^{2}} = 2 (k + 1) \frac{(n^{2} - 1) \sin i}{{(n^{2} - 1 + \cos^{2} i)}^{3 / 2}}$

La derivada segunda es positiva ya que n>1.

Arco primario

El arco primario se forma cuando k=1, hay una sola reflexión interna.

En color azul claro, el rayo cuyo ángulo de incidencia da lugar a una desviación mínima.

Creamos un script para representar el ángulo de desviación D en función del ángulo de incidencia i. Fijamos el número de reflexiones internas k=1 (arco primario) y la longitud de onda λ en nanómetros

k=1;  %número de reflexiones internas
lonOnda=671;  %longitud de onda en nm
n=1.324+3084.3/lonOnda^2; % índice de refracción
x=55:0.1:65;
%x es el ángulo incidente, 
%el ángulo refractado, sin(x)=n·sin(r), r=asin(sin(x)/n)
D=(k*pi+2*(x*pi/180)-2*(k+1)*asin(sin(x*pi/180)/n))*180/pi;
plot(x,D)
xlabel('i')
ylabel('D')
title('Angulo de desviación')
grid on
[xmin,nmin]=min(D);
fprintf('El mínimo de desviación se produce para el 
ángulo %2.2f y vale %3.2f\n',x(nmin), xmin)

El mínimo de desviación se produce para el 
        ángulo 59.50 y vale 137.61

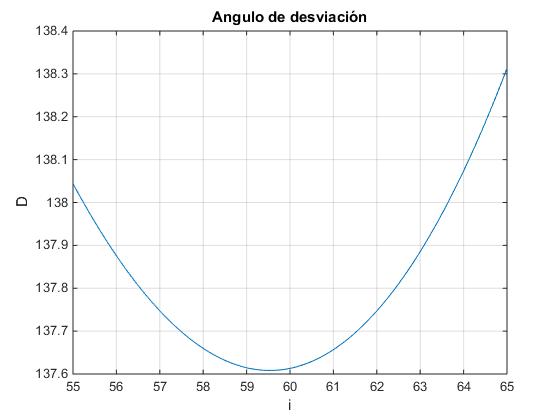
En la figura, se muestra la desviación D en función de ángulo de incidencia, para la luz de color rojo, λ=671 nm, el valor mínimo se obtiene para i=59.5º, el ángulo de desviación vale D_m=137.6º

Arco secundario

El arco primario se forma cuando k=2, hay dos reflexiones internas.

En color azul claro, el rayo cuyo ángulo de incidencia da lugar a una desviación mínima.

Modificamos el script anterior, para mostrar el ángulo de desviación D en función del ángulo incidente i cuando el número de reflexiones internas k=2

k=2;  %número de reflexiones internas
lonOnda=671;  %longitud de onda en nm
n=1.324+3084.3/lonOnda^2; % índice de refracción
x=65:0.1:75;
%x es el ángulo incidente, 
%el ángulo refractado, sin(x)=n·sin(r), r=asin(sin(x)/n)
D=(k*pi+2*(x*pi/180)-2*(k+1)*asin(sin(x*pi/180)/n))*180/pi;
plot(x,D)
xlabel('i')
ylabel('D')
title('Angulo de desviación')
grid on
[xmin,nmin]=min(D);
fprintf('El mínimo de desviación se produce para el 
ángulo %2.2f y vale %3.2f\n',x(nmin), xmin)

El mínimo de desviación se produce para el 
        ángulo 71.90 y vale 230.33

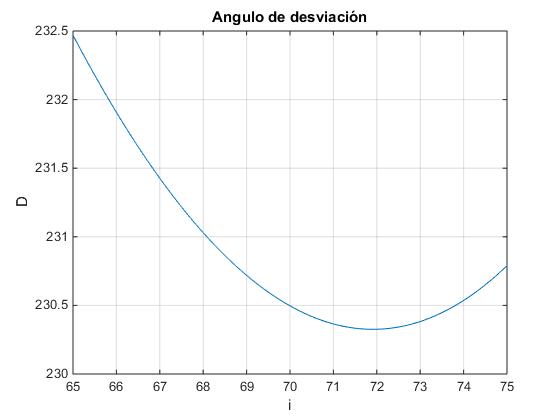
En la figura, se muestra la desviación D en función de ángulo de incidencia, para la luz de color rojo, λ=671 nm, el valor mínimo se obtiene para i=71.9º, el ángulo de desviación vale D_m=230.3º

Angulo de desviación mínima

Las fórmulas que precisamos para calcular el ángulo de desviación mínimo son las siguientes:

Indice de refracción n en función de la longitud de onda λ en nm

n=1.324+3084.3/λ²

Ley de Snell

sini=n·sinr

Ángulo incidente i que da lugar a la mínima desviación y desviación mínima D_m.

$\cos i = \sqrt{\frac{n^{2} - 1}{k (k + 2)}} D = k \cdot 180 + 2 i - 2 (k + 1) r$

Arco, k	Rojo, λ=671 nm,		Violeta, λ=404 nm,		ΔD
Arco, k	i	D_m	i	D_m	ΔD
1	59.5º	137.6º	58.8º	139.3º	1.7º
2	71.9º	230.3º	71.5º	233.4º	3.1º

En la última columna, tenemos la anchura angular ΔD de los arcos primario y secundario. El arco secundario es casi el doble de ancho que el primario.
El ángulo de la zona oscura de Alejandro Δφ es la diferencia entre el ángulo del rojo en el arco primario visto por el observador terrestre φ₁=180-137.6=42.4º y el rojo del arco secundario visto por el mismo observador φ₂=230.3-180=50.3º. Δφ=φ₂-φ₁=7.9º. Véase la tercera figura de esta página.

Intensidad y polarización de la luz

Las ecuaciones de Fresnel nos dan los coeficientes de reflexión y de transmisión de las ondas electromagnéticas en la separación entre dos medios no conductores.

$\begin{array}{l} R_{N} = {(\frac{n_{1} \cos θ_{i} - n_{2} \cos θ_{t}}{n_{1} \cos θ_{i} + n_{2} \cos θ_{t}})}^{2} T_{N} = \frac{4 n_{1} n_{2} \cos θ_{i} \cos θ_{t}}{{(n_{1} \cos θ_{i} + n_{2} \cos θ_{t})}^{2}} \\ R_{P} = {(\frac{- n_{2} \cos θ_{i} + n_{1} \cos θ_{t}}{n_{2} \cos θ_{i} + n_{1} \cos θ_{t}})}^{2} T_{P} = \frac{4 n_{1} n_{2} \cos θ_{i} \cos θ_{t}}{{(n_{2} \cos θ_{i} + n_{1} \cos θ_{t})}^{2}} \end{array}$

Fuente: Lorrain P. Corson D. L. Campos y Ondas Electromagnéticas. Selecciones Científicas (1972) pág. 554

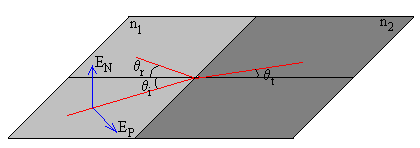
En el primer caso, el campo eléctrico E_N es perpendicular al plano de incidencia
En el segundo caso, el campo eléctrico E_P está contenido en el plano de incidencia

Vamos a calcular las intensidades relativas de los rayos que dan lugar al arco primario y secundario.

Un rayo de luz no polarizada de longitud de onda λ, incide sobre una gota de agua de índice de refracción n₂=n, que a su vez depende de la longitud de onda. El índice de refracción del aire es constante e igual a n₁=1. Parte de la luz incidente se refleja y otra parte se refracta. Si el ángulo de incidencia es θ_i=i y el ángulo que forma la luz refractada con la normal es θ_t=r. Los coeficientes se expresan

$\begin{array}{l} R_{N} = {(\frac{\cos i - n \cos r}{\cos i + n \cos r})}^{2} T_{N} = 1 - R_{N} \\ R_{P} = {(\frac{- n \cos i + \cos r}{n \cos i + \cos r})}^{2} T_{P} = 1 - R_{P} \end{array}$

Vamos a calcular los coeficientes para la luz de color rojo, λ=671 nm, n=1.331

Arco primario (k=1)

El ángulo de incidencia que corresponde a la desviación mínima es i=59.54º

El ángulo r se calcula aplicando la ley de Snell, sini=n·sinr

En (1) tenemos que una parte de la luz se transmite y otra parte se refleja.

Proporción de luz transmitida polarizada N, T_1N=0.88880
Proporción de luz transmitida polarizada P, T_1P=0.99631

La luz atraviesa la gota y en (2) tenemos que una parte se refleja en su superficie interior y otra se transmite.

Los datos ahora son: n₂=1, n₁=n. El ángulo de incidencia es θ_i=r y el ángulo que forma la luz refractada con la normal es θ_t=i.

$\begin{array}{l} R'_{N} = {(\frac{n \cos r - \cos i}{n \cos r + \cos i})}^{2} = R_{N} \\ R'_{P} = {(\frac{- \cos r + n \cos i}{\cos r + n \cos i})}^{2} = R_{P} \end{array}$

que son las mismas fórmulas que hemos obtenido anteriormente

Proporción de luz reflejada polarizada N, R_2N=T_N·R_N=0.09883
Proporción de luz reflejada polarizada P, R_2P=T_P·R_P=0.00367

La luz atraviesa la gota y en (3) tenemos que una parte se refleja en su superficie interior y otra se transmite.

Los datos ahora son: n₂=1, n₁=n. El ángulo de incidencia es θ_i=r y el ángulo que forma la luz refractada con la normal es θ_t=i.

Proporción de luz trasmitida polarizada N, T_3N=T_N·R_N T_N·=0.08784
Proporción de luz trasmitida polarizada P, T_3P=T_P·R_P T_P=0.00366

La relación T_3N/T_3P=24

Total, I=T_3N+T_3P=915·10^-4

Arco secundario (k=2)

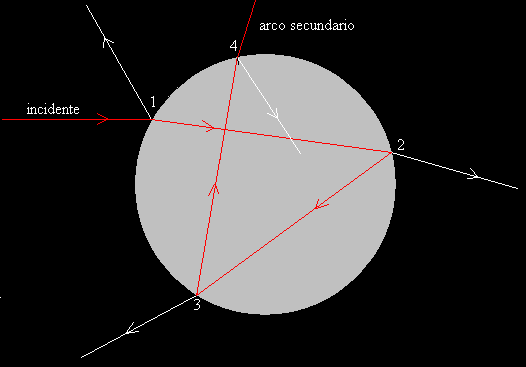
El ángulo de incidencia que corresponde a la desviación mínima es i=71.92º

El ángulo r se calcula aplicando la ley de Snell, sini=n·sinr,

En (1) tenemos que una parte de la luz se transmite y otra parte se refleja.

Proporción de luz transmitida polarizada N, T_1N=0.74977
Proporción de luz transmitida polarizada P, T_1P=0.93357

La luz atraviesa la gota y en (2) tenemos que una parte se refleja en su superficie interior y otra se transmite.

Proporción de luz reflejada polarizada N, R_2N=T_N·R_N=0.18761
Proporción de luz reflejada polarizada P, R_2P=T_P·R_P=0.06201

La luz atraviesa la gota y en (3) tenemos que una parte se refleja en su superficie interior y otra se transmite.

Proporción de luz reflejada polarizada N, R_3N=T_N·R_N R_N·=0.04695
Proporción de luz reflejada polarizada P, R_3P=T_P·R_P R_P=0.00412

La luz atraviesa la gota en (4) tenemos que una parte se refleja en su superficie interior y otra se transmite.

Proporción de luz transmitida polarizada N, T_4N=T_N·R_N R_N·T_N =0.03520
Proporción de luz transmitida polarizada P, T_4P=T_P·R_P R_P·T_P =0.00384

La relación T_4N/T_4P=9

Total, I=T_4N+T_4P=390.4·10^-4

La luz proveniente del arco iris primario está mucho más polarizada que la proveniente del arco secundario.

En general, después de k reflexiones internas la intensidad del rayo trasmitido es

$\begin{array}{l} T_{N} = {(1 - R_{N})}^{2} R_{N}^{k} = {(1 - {(\frac{\cos i - n \cos r}{\cos i + n \cos r})}^{2})}^{2} {(\frac{\cos i - n \cos r}{\cos i + n \cos r})}^{2 k} \\ T_{P} = {(1 - R_{P})}^{2} R_{P}^{k} = {(1 - {(\frac{- n \cos i + \cos r}{n \cos i + \cos r})}^{2})}^{2} {(\frac{- n \cos i + \cos r}{n \cos i + \cos r})}^{2 k} \\ T = T_{N} + T_{P} \end{array}$

Los valores de T_N y T_P para los arcos supernumerarios (k>2) son muy pequeños.

Actividades

Se introduce

El orden del arco k, en el control titulado Reflexiones internas.
El ángulo de incidencia i, en el control titulado Angulo incidente
La longitud de onda de la radiación monocromática, dentro del espectro visible en el control titulado Longitud onda

Se pulsa el botón titulado Nuevo

El programa interactivo calcula el ángulo de desviaciación D, y los coeficientes I_P e I_N que hay que multiplicar por 10^-4. La magnitud relativa de estos coeficientes nos da una idea acerca de la polarización de la luz y su suma de la reducción de la intensidad de la luz.

Se sugiere al lector que para el color violeta λ=404 nm, calcule

El índice de refracción n.
El ángulo de incidencia que da lugar a la desviación mínima para el arco primario (k=1) y para el secundario (k=2)
La desviación mínima en ambos casos.
Los valores de T_3N y T_3P para el arco primario
Los valores de T_4N y T_4P para el arco secundario

Reflexiones internas:
Angulo incidente:
Longitud onda (380-780 nm):

En el siguiente programa, se muestra las trayectorias de todos los rayos monocromáticos, para sus ángulos de desviación mínima, respectivos. Se muestran los valores numéricos de las desviaciones mínimas de los rayos cuya longitud de onda corresponde a los extremos del espectro visible: rojo 780 nm, violeta 380 nm.

Reflexiones internas:

Interferencia. Arcos supernumerarios.

Cuando una gota se ilumina con luz monocromática, en vez de una estrecha banda de luz para el ángulo de desviación mínima D_m correspondiente a dicho color, se observa un diagrama de interferencia en la que el máximo principal de intensidad no se corresponde exactamente con el ángulo de desviación mínima, sino que está ligeramente desplazado. Se observan también máximos secundarios de intensidad incluso a ángulos más grandes que D_m.

Airy en 1838 estudió la interferencia de los rayos de longitud de onda λ cercanos al rayo cartesiano que se reflejan y refractan en una gota de radio a. La intensidad I para un ángulo de desviación D se obtiene (véase el artículo de Berry y Klein citado en las referencias)

$\begin{array}{l} I (z) = K {Ai}^{2} (- z) \\ z = (D - D_{m}) \frac{{(n^{2} - 1)}^{1 / 2}}{{(4 - n^{2})}^{1 / 6}} (\frac{4 π a}{3 λ}) \end{array}$

Las funciones de Airy se describen en la página titulada Potencial en forma de V

Angulo de desviación

Calculamos el ángulo de desviación mínima correspondientes al color verde, λ=530 nm, para k=1 y para k=2 (reflexiones internas)

lonOnda=530;  %longitud de onda en nm
n=1.324+3084.3/lonOnda^2; % índice de refracción

k=1;  %número de reflexiones internas
x=55:0.1:65;
%x es el ángulo incidente, 
%el ángulo refractado, sin(x)=n sin(r), r=asin(sin(x)/n)
D=(k*pi+2*(x*pi/180)-2*(k+1)*asin(sin(x*pi/180)/n))*180/pi;
subplot(2,1,1)
plot(x,D)
[xmin,nmin]=min(D);
texto=sprintf(' %2.2f --> %3.2f\n',x(nmin), xmin);
text(60,138.8, texto)
xlabel('i')
ylabel('D')
title('Angulo de desviación, k=1')
grid on

k=2;  %número de reflexiones internas
x=65:0.1:75;
%x es el ángulo incidente, 
%el ángulo refractado, sin(x)=n sin(r), r=asin(sin(x)/n)
D=(k*pi+2*(x*pi/180)-2*(k+1)*asin(sin(x*pi/180)/n))*180/pi;
subplot(2,1,2)
plot(x,D)
[xmin,nmin]=min(D);
texto=sprintf(' %2.2f --> %3.2f\n',x(nmin), xmin);
text(70,233, texto)
xlabel('i')
ylabel('D')
title('Angulo de desviación, k=2')
grid on

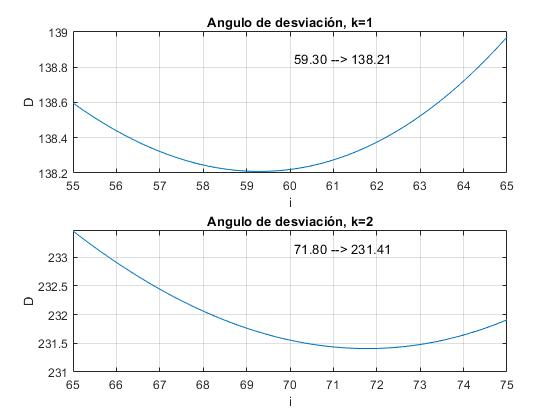
Arco secundario (k=2)

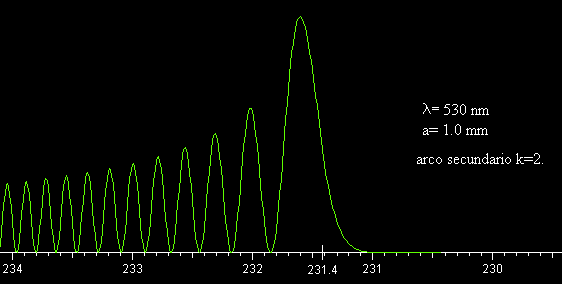
En la figura, se representa la intensidad I(D), en las proximidades del ángulo de desviación mínima D_m correspondiente al color verde λ=530 nm. La gota tiene un radio de a=1.0 mm. El ángulo de desviación mínima es de D_m=231.4º y está señalado en el eje horizontal. El máximo principal de intensidad se obtiene para un ángulo ligeramente mayor. Para ángulos un poco menores que D_m la intensidad es prácticamente nula (zona oscura de Alejandro). Para ángulos mayores que D_m la intensidad oscila entre valores máximos y mínimos dando lugar a franjas de interferencia.

Arco primario (k=1)

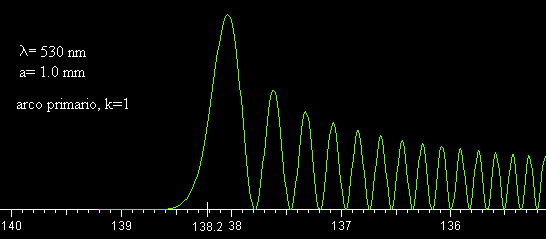
En la figura, se representa la intensidad I(D), para la misma gota y radiación monocromática. El ángulo de desviación mínima es de D_m=138.2º y está señalado en el eje horizontal. El máximo principal de intensidad se obtiene para un ángulo ligeramente menor. Para ángulos un poco mayores que D_m la intensidad es prácticamente nula (zona oscura de Alejandro). Para ángulos menores que D_m la intensidad oscila entre valores máximos y mínimos dando lugar a franjas de interferencia, que se denominan arcos supernumerarios dentro del arco primario.

Lo que realmente vemos en un arco iris es la suma de las franjas de interferencia para todos los colores del espectro visible. Algunos arcos supernumerarios son a veces visibles en el interior del arco primario, coloreados alternativamente rosa y verde, pero son difícilmente visibles fuera del arco secundario.

Actividades

Se introduce

El radio de la gota a en mm, en el control titulado Radio gota
La longitud de onda de la luz monocromática que ilumina la gota, en el control titulado Longitud onda

Se pulsa el botón titulado Nuevo

Se representa en el eje horizontal el ángulo del arco primario (180-138.2=41.8) y secundario (231.4-180=51.4) visto por el observador terrestre y en el eje vertical la intensidad de la radiación monocromática seleccionada. En medio, la zona obscura de Alejandro. Los arcos supernumerarios representados por las oscilaciones de la intensidad o en la parte central, por la sucesión de franjas de color gris claro y oscuro.

Longitud onda (380-780 nm):
Radio gota:

Referencias.

Whitaker R. J. Physics of the rainbow. The Physics Teacher. Vol 12, May 1974, pp. 283-286.

Hendry A. W. A tripe rainbow?. The Physics Teacher Vol 41, November 2003, pp. 460-463.

Nussenzveig H. M. Teoría del arco iris. Investigación y Ciencia, nº 9, Junio 1977, págs. 82-94.

Walker J. D., Multiple rainbows from single drops of water and other liquids. Am. J. Phys. Vol. 44 nº 5, May 1976, pp. 421-433

M. V. Berry, S Klein. Diffraction near fake caustics. Eur. J. Phys. 18 (1997) pp. 303-306

La función de Ai(x) ha sido adaptada al lenguaje JavaScript desde su versión en lenguaje Java