Posición aparente de un objeto debajo del agua

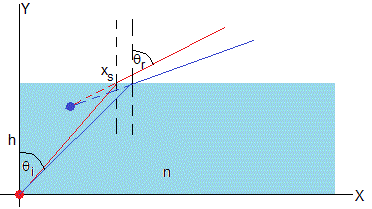
Primero, vamos a resolver una situación más simple. Dado el ángulo de incidencia, determinaremos la posición aparente de un objeto vista por un nadador que se encuentra en la dirección del rayo refractado

El objeto está situado en el origen a una profundidad h. Del objeto parte un rayo (color rojo) que forma un ángulo de incidencia θ_i. El rayo refractado forma un ángulo θ_r con la normal. De acuerdo con la ley de la refracción

nsinθ_i=sinθ_r

siendo n=1.33 el índice de refracción del agua y 1 el índice de refracción del aire. El ángulo de refracción θ_r es mayor que el incidente θ_i.

La dirección del rayo refractado y su prolongación pasa por el punto (x_s,h) y su pendiente es 1/tanθ_r. Sabiendo que x_s=htanθ_i. La ecuación de esta recta es

$y - h = \frac{x - x_{s}}{\tan θ_{r}}$

Del objeto parte un rayo (color azul) que forma un ángulo de incidencia θ'_i. El rayo refractado forma un ángulo θ'_r con la normal.

La dirección del rayo refractado y su prolongación pasa por el punto (x'_s,h) y su pendiente es 1/tanθ'_r. Sabiendo que x'_s=htanθ'_i. La ecuación de esta recta es

$y - h = \frac{x - x_{s}^{'}}{\tan θ_{r}^{'}}$

Las prolongaciones de los rayos refractados se cortan el en punto señalado en color azul de coordenadas

$\begin{array}{l} x_{a} = \frac{\tan θ_{i} \tan θ_{r}^{'} - \tan θ_{r} \tan θ_{i}^{'}}{\tan θ_{r}^{'} - \tan θ_{r}} h \\ y_{a} = (1 - \frac{\tan θ_{i}^{'} - \tan θ_{i}}{\tan θ_{r}^{'} - \tan θ_{r}}) h \end{array}$

Esta es la posición (x_a, y_a) aparente del objeto visto por un observador que se encuentra en la dirección del rayo refractado. Donde θ'_i=θ_i+δ, siendo δ un incremento de ángulo pequeño.

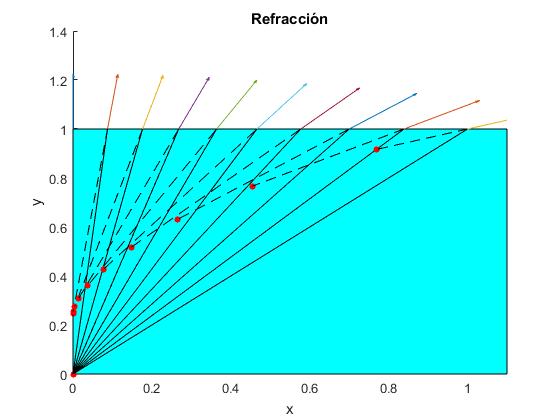
Representamos la posición aparente (x_a, y_a) de un objeto situado en el origen, para varios ángulos de incidencia

La profundidad del objeto es h=1 m, el incremento de ángulo δ=0.01 grados. Las flechas indican la dirección del rayo refractado, la dirección de observación del objeto

n=1.33; %índice de refracción del agua
delta=0.01*pi/180; %0.01 grado
h=1; %profundidad
hold on
%piscina
x=[0,0,1.1,1.1];
y=[0,1,1,0];
fill(x,y,'c')
plot(0,0,'ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
for aIn=(0:5:45)*pi/180
    aRe=asin(n*sin(aIn)); %ángulo de refracción
    aRe_p=asin(n*sin(aIn+delta)); %ángulo de refracción
    xa=sin(aIn)^3*(n^2-1)*h/cos(aIn)^3;
    ya=(1-(1-n^2*sin(aIn)^2)^(3/2)*h/(n*cos(aIn)^3));
    plot(xa,ya,'ro','markersize',4,'markeredgecolor','r','markerfacecolor','r')
    xs=h*tan(aIn);
    line([0,xs],[0,h],'color','k')
    line([xs,xa],[h,ya],'lineStyle','--','color','k')
    quiver(xs,h,0.25*sin(aRe),0.25*cos(aRe));
end
hold off
xlim([0,1.1])
xlabel('x')
ylabel('y')
title('Refracción')

Se fija la posición del observador

En esta sección vamos a describir la posición aparente de los objetos sumergidos en una piscina respecto de un nadador situado en el borde

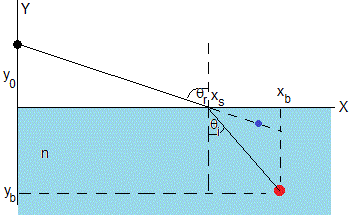
El eje Y coincide con la posición del nadador y el eje X con la superficie del agua. La posición de los ojos del nadador es (0,y₀) y la posición del objeto sumergido (punto de color rojo) en el agua es (x_b, y_b), la posición aparente del objeto (punto de color azul) es (x_a, y_a)

Un rayo incidente procedente del objeto, se refracta en un punto de la superficie de separación de los dos medios situado a x_s, formando un ángulo θ_i con la normal. El rayo refractado llega a los ojos del observador formando un ángulo θ_r con la normal.

Conocida la posición del objeto (x_b, y_b) y la de los ojos del nadador (0,y₀), a partir de la ley de la refracción, nsinθ_i=sinθ_r, vamos a calcular la posición x_s donde se refracta el rayo de luz procedente del objeto y los ángulo de incidencia θ_i y el refractado θ_r. En la figura vemos que

$\tan θ_{i} = \frac{x_{b} - x_{s}}{- y_{b}} \tan θ_{r} = \frac{x_{s}}{y_{0}}$

Eliminado x_s y utilizando la ley de la refracción

$\begin{array}{l} x_{b} - y_{0} \tan θ_{r} + y_{b} \frac{\sin θ_{i}}{\sqrt{1 - \sin^{2} θ_{i}}} = 0 \\ x_{b} - y_{0} \frac{\sin θ_{r}}{\sqrt{1 - \sin^{2} θ_{r}}} + y_{b} \frac{\sin θ_{r}}{\sqrt{n^{2} - \sin^{2} θ_{r}}} = 0 \end{array}$

Resolvemos esta ecuación transcendente, para calcular θ_r, después x_s y θ_i

La ecuación de la dirección del rayo refractado y su prolongación es

$\begin{array}{l} y = - \frac{x - x_{s}}{\tan θ_{r}} \\ x_{b} - x = y \tan θ_{r} - y_{b} \tan θ_{i} \end{array}$

Para determinar la posición aparente del objeto, precisamos trazar un rayo más de ángulo de refracción θ'_r= θ_r+δ, (siendo δ un ángulo muy pequeño, infinitesimal) y hallar la intersección de la prolongación de los dos rayos refractados, tal como se muestra exageradamente en la figura. Las ecuaciones de las rectas de color rojo y azul son, respectivamente

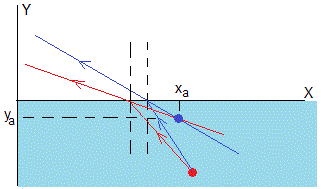
${\begin{cases} x_{b} - x = y \tan θ_{r} - y_{b} \tan θ_{i} \\ x_{b} - x = y \tan θ_{r}^{'} - y_{b} \tan θ_{i}^{'} \end{cases}$

Despejamos la posición aparente x_a e y_a que es el punto de intersección de las dos rectas

${\begin{cases} x_{a} = x_{b} - y_{b} \frac{\tan θ_{i}^{'} \tan θ_{r} - \tan θ_{r}^{'} \tan θ_{i}}{\tan θ_{r}^{'} - \tan θ_{r}} \\ y_{a} = y_{b} \frac{\tan θ_{i}^{'} - \tan θ_{i}}{\tan θ_{r}^{'} - \tan θ_{r}} \end{cases}$

Calculamos la ordenada y_a

$\begin{array}{l} \frac{\tan θ_{i}^{'} - \tan θ_{i}}{\tan θ_{r}^{'} - \tan θ_{r}} = \frac{\frac{\sin θ_{r}^{'}}{\sqrt{n^{2} - \sin^{2} θ_{r}^{'}}} - \frac{\sin θ_{r}}{\sqrt{n^{2} - \sin^{2} θ_{r}}}}{\tan θ_{r}^{'} - \tan θ_{r}} = \\ \frac{\frac{\sin (θ_{r} + δ)}{\sqrt{n^{2} - \sin^{2} (θ_{r} + δ)}} - \frac{\sin θ_{r}}{\sqrt{n^{2} - \sin^{2} θ_{r}}}}{\tan (θ_{r} + δ) - \tan θ_{r}} \end{array}$

Hacemos la aproximación

$\begin{array}{l} f (θ_{r} + δ) \approx f (θ_{r}) + \frac{d f}{d θ_{r}} δ \\ \tan (θ_{r} + δ) \approx \tan θ_{r} + \frac{δ}{\cos^{2} θ_{r}} \\ \frac{\sin (θ_{r} + δ)}{\sqrt{n^{2} - \sin^{2} (θ_{r} + δ)}} \approx \frac{\sin θ_{r}}{\sqrt{n^{2} - \sin^{2} θ_{r}}} + \frac{n^{2} \cos θ_{r}}{{(n^{2} - \sin^{2} θ_{r})}^{3 / 2}} δ \end{array}$

El resultado final es

$\begin{array}{l} y_{a} = y_{b} \frac{{\frac{\sin θ_{r}}{\sqrt{n^{2} - \sin^{2} θ_{r}}} + \frac{n^{2} \cos θ_{r}}{{(n^{2} - \sin^{2} θ_{r})}^{3 / 2}} δ} - \frac{\sin θ_{r}}{\sqrt{n^{2} - \sin^{2} θ_{r}}}}{{\tan θ_{r} + \frac{δ}{\cos^{2} θ_{r}}} - \tan θ_{r}} \\ = y_{b} \frac{n^{2} \cos^{3} θ_{r}}{{(n^{2} - \sin^{2} θ_{r})}^{3 / 2}} \end{array}$

Calculamos la abscisa x_a

$\begin{array}{l} \frac{\tan θ_{i}^{'} \tan θ_{r} - \tan θ_{r}^{'} \tan θ_{i}}{\tan θ_{r}^{'} - \tan θ_{r}} = \frac{\frac{\sin θ_{i}^{'}}{\sqrt{1 - \sin^{2} θ_{i}^{'}}} \tan θ_{r} - \tan θ_{r}^{'} \frac{\sin θ_{i}}{\sqrt{1 - \sin^{2} θ_{i}}}}{\tan θ_{r}^{'} - \tan θ_{r}} = \\ \frac{\frac{\sin θ_{r}^{'}}{\sqrt{n^{2} - \sin^{2} θ_{r}^{'}}} \tan θ_{r} - \tan θ_{r}^{'} \frac{\sin θ_{r}}{\sqrt{n^{2} - \sin^{2} θ_{r}}}}{\tan θ_{r}^{'} - \tan θ_{r}} = \\ \frac{\frac{\sin (θ_{r} + δ)}{\sqrt{n^{2} - \sin^{2} (θ_{r} + δ)}} \tan θ_{r} - \tan (θ_{r} + δ) \frac{\sin θ_{r}}{\sqrt{n^{2} - \sin^{2} θ_{r}}}}{\tan (θ_{r} + δ) - \tan θ_{r}} \approx \\ \frac{{\frac{\sin θ_{r}}{\sqrt{n^{2} - \sin^{2} θ_{r}}} + \frac{n^{2} \cos θ_{r}}{{(n^{2} - \sin^{2} θ_{r})}^{3 / 2}} δ} \tan θ_{r} - {\tan θ_{r} + \frac{δ}{\cos^{2} θ_{r}}} \frac{\sin θ_{r}}{\sqrt{n^{2} - \sin^{2} θ_{r}}}}{{\tan θ_{r} + \frac{δ}{\cos^{2} θ_{r}}} - \tan θ_{r}} \end{array}$

El resultado final es

$x_{a} = x_{b} + y_{b} \frac{(n^{2} - 1) \sin^{3} θ_{r}}{{(n^{2} - \sin^{2} θ_{r})}^{3 / 2}}$

Cálculo de la posición aparente de un objeto sumergido

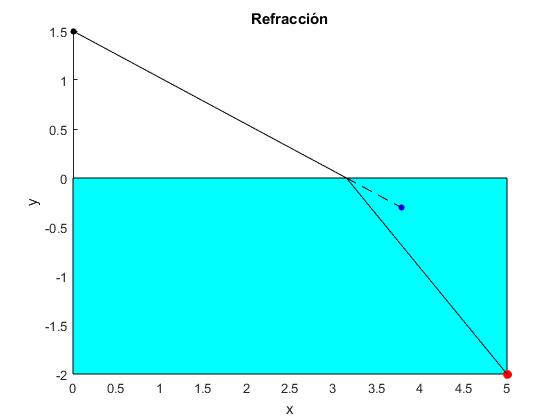
Sea y₀=1.5 la altura de los ojos de nadador, la posición del objeto (x_b, y_b) es (5,-2)m

Resolvemos la ecuación transcendente para calcular el ángulo del rayo refractado θ_r y la posición x_s en la superficie del agua donde se refracta el rayo incidente

$x_{b} - y_{0} \frac{\sin θ_{r}}{\sqrt{1 - \sin^{2} θ_{r}}} + y_{b} \frac{\sin θ_{r}}{\sqrt{n^{2} - \sin^{2} θ_{r}}} = 0$

y posteriormente, las posición aparente (x_a, y_a) de un objeto situado en la posición (x_b, y_b)

${\begin{cases} x_{a} = x_{b} + y_{b} \frac{(n^{2} - 1) \sin^{3} θ_{r}}{{(n^{2} - \sin^{2} θ_{r})}^{3 / 2}} \\ y_{a} = y_{b} \frac{n^{2} \cos^{3} θ_{r}}{{(n^{2} - \sin^{2} θ_{r})}^{3 / 2}} \end{cases}$

Trazamos el rayo incidente, el refractado y su prolongación hasta la posición aparente del objeto

n=1.33; %índice de refracción del agua
xb=5; %distancia al objeto
yb=-2; %profundidad
y0=1.5; %observador
f=@(x) xb-y0*x/sqrt(1-x^2)+yb*x/sqrt(n^2-x^2); % x es sin(th)
th_r=asin(fzero(f,[0,0.99]));
hold on
%piscina
x=[0,5,5,0];
y=[0,0,-2,-2];
hold on
fill(x,y,'c')
plot(xb,yb,'ro','markersize',6,'markeredgecolor','r','markerfacecolor','r')
plot(0,y0,'ko','markersize',4,'markeredgecolor','k','markerfacecolor','k')
xa=xb+yb*(n^2-1)*sin(th_r)^3/(n^2-sin(th_r)^2)^(3/2);
ya=yb*n^2*cos(th_r)^3/(n^2-sin(th_r)^2)^(3/2);
plot(xa,ya,'bo','markersize',4,'markeredgecolor','b','markerfacecolor','b')
xs=y0*tan(th_r);
line([xb,xs],[yb,0],'color','k')
line([0,xs],[y0,0],'color','k')
line([xs,xa],[0,ya],'lineStyle','--','color','k')
hold off
xlabel('x')
ylabel('y')
title('Refracción')

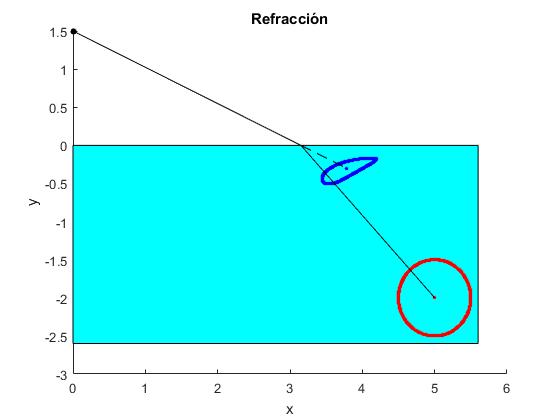
Elaboramos un script para dibujar la apariencia de un objeto de forma circular de radio 0.5 situado en el fondo de una piscina. La posición del centro del objeto es (5,-2) m y el observador está en el borde de la piscina a y₀=1.5

n=1.33; %índice de refracción del agua
y0=1.5; %observador
%objeto
t=(1:360)*pi/180;
Xb=[0.5*cos(t),0]+5;
Yb=[0.5*sin(t),0]-2;
%piscina
x=[0,5.6,5.6,0];
y=[0,0,-2.6,-2.6];
hold on
fill(x,y,'c')
%observador
plot(0,y0,'ko','markersize',4,'markeredgecolor','k','markerfacecolor','k')
for i=1:length(Xb)
    xb=Xb(i);
    yb=Yb(i);
    f=@(x) xb-y0*x/sqrt(1-x^2)+yb*x/sqrt(n^2-x^2);
    th_r=asin(fzero(f,[0,0.99]));
    plot(xb,yb,'ro','markersize',2,'markeredgecolor','r','markerfacecolor','r')
    xa=xb+yb*(n^2-1)*sin(th_r)^3/(n^2-sin(th_r)^2)^(3/2);
    ya=yb*n^2*cos(th_r)^3/(n^2-sin(th_r)^2)^(3/2);
    plot(xa,ya,'bo','markersize',2,'markeredgecolor','b','markerfacecolor','b')
end
xs=y0*tan(th_r);
line([xb,xs],[yb,0],'color','k')
line([0,xs],[y0,0],'color','k')
line([xs,xa],[0,ya],'lineStyle','--','color','k')
hold off
xlabel('x')
ylabel('y')
title('Refracción')

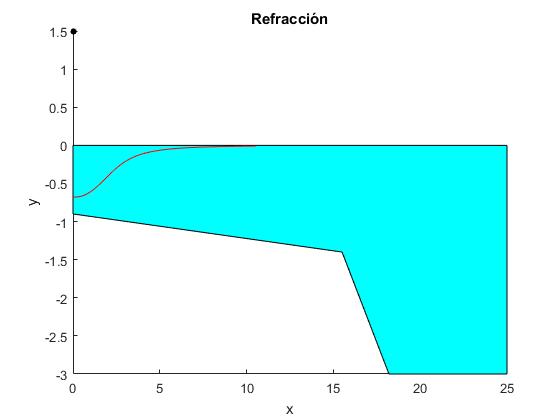
Finalmente, dibujamos la forma aparente del fondo de una piscina vista por el nadador situado en el borde. La forma real está descrita por la función

$y_{b} = {\begin{cases} - 0.9 - \frac{0.5 x_{b}}{15.5} 0 \leq x_{b} < 15.5 \\ \frac{- 1.6 x_{b} + 21.02}{2.7} 15.5 \leq x_{b} < 18.2 \\ - 3 18.2 \leq x_{b} \leq 25 \end{cases}$

n=1.33; %índice de refracción del agua
y0=1.5; %observador
g=@(x) (-0.9-0.5*x/15.5).*(x<15.5)+(-1.6*x+21.02).*(x>=15.5 && x<18.2)/2.7
-3*(x>=18.2 && x<=25);
xb=0:0.1:25;
yb=zeros(1,length(xb));
xa=zeros(1,length(xb));
ya=zeros(1,length(xb));
for i=1:length(xb)
    yb(i)=g(xb(i));
end
%yb=fliplr(yb);
for i=1:length(xb)
    f=@(x) xb(i)-y0*x/sqrt(1-x^2)+yb(i)*x/sqrt(n^2-x^2);
    if sign(f(0))==sign(f(0.99))
        break;
    else
        th_r=asin(fzero(f,[0,0.99]));
    end
    xa(i)=xb(i)+yb(i)*(n^2-1)*sin(th_r)^3/(n^2-sin(th_r)^2)^(3/2);
    ya(i)=yb(i)*n^2*cos(th_r)^3/(n^2-sin(th_r)^2)^(3/2);
end
hold on
%observador
plot(0,y0,'ko','markersize',4,'markeredgecolor','k','markerfacecolor','k')
fill([25,0,xb],[0,0,yb],'c')
plot(xa(1:i-1),ya(1:i-1),'r')
hold off
xlabel('x')
ylabel('y')
title('Refracción')

Invertimos el perfil de la piscina, de modo que la parte más profunda esté más cerca del observador

Utilizamos la función fliplr de MATLAB para invertir el orden de los elementos del vector y_b. Basta por tanto, añadir al script la sentencia

...
for i=1:length(xb)
    yb(i)=g(xb(i));
end
yb=fliplr(yb);
for i=1:length(xb)
...

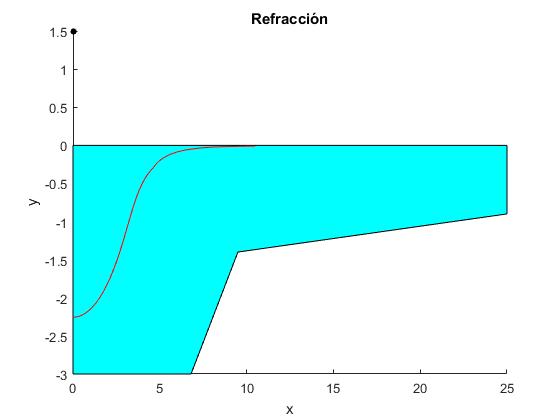
El nadador no aprecia el fondo de la piscina a partir de cierta distancia x_b de alrededor 6 m, para la cual y_a se hace casi cero

Referencias

Kenneth S. Mendelson. Apparent shape of a swimming pool. Am. J. Phys. 78 (12). December 2010, pp.1254-1257

R Arizaga, N Cap, H Rabal, M Trivi. Image distortion due to refraction by planar surfaces. Eur. J. Phys. 31 (2010) pp. 115-127