Observación de un objeto cercano

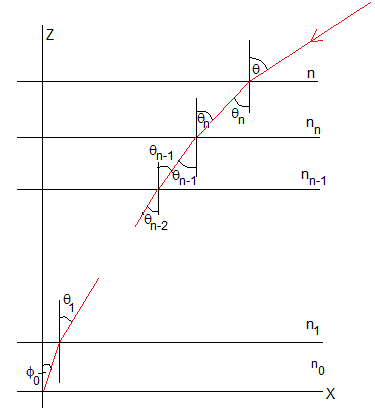
Cuando observamos un objeto cercano a la superficie de la Tierra, comparado con su radio, consideramos la Tierra como plana.

Supongamos que la atmósfera está formada por capas con índices de refracción n₀ (en la superficie), n₁, n₂...n_n-1, n_n, y n (por encima de la atmósfera). Sea θ el ángulo que forma el rayo incidente con el eje vertical Z al entrar en la atmósfera, este se propaga por las distintas capas, siguiendo la ley de la refracción

nsinθ=n_nsinθ_n
n_nsinθ_n=n_n-1sinθ_n-1
n_n-1sinθ_n-1=n_n-2sinθ_n-2
.........
n₁sinθ₁= n₀sinϕ₀

ϕ₀ es el ángulo de observación en la superficie de la Tierra (posición aparente del objeto observado).

La secuencia de igualdades lleva a, nsinθ=n₀sinϕ₀

Dado que el índice de refracción disminuye con la altura, los ángulos θ, θ_n, θ_n-1, ... θ₁ y ϕ₀ forman una serie decreciente. Por lo que ϕ₀ es más pequeño que θ, el objeto observado se ve más cerca del eje Z que si no hubiera atmósfera.

Se denomina ángulo de refracción a la diferencia, ΔR=θ-ϕ₀

${\displaystyle \begin{array}{l}n\sin \left({\varphi }_0+\Delta R\right)=n_0\sin {\varphi }_0\\ n\sin {\varphi }_0\cos \Delta R+n\cos {\varphi }_0\sin \Delta R=n_0\sin {\varphi }_0\\ n\sin {\varphi }_0+n\cos {\varphi }_0·\Delta R=n_0\sin {\varphi }_0\\ \Delta R=\left(\frac{n_0}{n}-1\right)\tan {\varphi }_0\end{array}}$

Como ΔR es un ángulo pequeño cosΔR≈1, y sinΔR≈ΔR

El ángulo de refracción ΔR es proporcional a la tangente del ángulo de observación ϕ₀

El índice de refracción de la parte superior de la atmósfera es n=1, el índice de refracción n₀ en la superficie de la Tierra dependerán de la densidad y la temperatura del aire. En condiciones estándar, n₀-1=0.00029.

Modelos simples de atmósfera

Cuando la distancia del objeto que observamos es muy grande, la Tierra y la atmósfera que la rodea no se pueden considerar planas.

En este apartado, vamos a familiarizarnos con la aplicación de la ley de la refracción a un problema con geometría esférica en vez de la plana a la que estamos acostumbrados. Supondremos que la atmósfera es una capa homogénea que rodea a la Tierra y a continuación, supondremos que está fomada for dos capas. En el siguiente apartado, analizaremos el problema de la variación continua del índice de refracción con la altura.

La atmósfera es una capa uniforme

La geometría esférica, complica la aplicación de la ley de la refracción, en comparación del caso plano estudiado en el apartado anterior. Empecemos por el caso más sencillo considerando que la atmósfera es una capa uniforme de altura h cuyo índice de refracción n

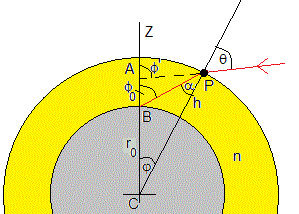
Sea θ, el ángulo de incidencia medido desde la dirección radial. La prolongación del rayo corta el eje Z en el punto A, formando un ángulo ϕ'

El rayo de luz se refracta formando un ángulo α con la dirección radial. Llega a la superficie de la Tierra, en B, formando un ángulo ϕ₀ con el eje Z, que es su posición aparente

El ángulo de refración es ΔR=ϕ'-ϕ₀

Calcularemos el ángulo de refración es ΔR a partir de la ley de la refracción y de la geometría del problema

Ley de la refracción, 1·sinθ=n·sinα

Triángulo PBC, ϕ₀=α+φ

${\displaystyle \frac{r_0}{\sin \alpha }=\frac{r}{\sin (180-{\varphi }_0)}}$

Triángulo PAC, ϕ'=θ+φ

De modo que ΔR=ϕ'-ϕ₀=θ-α, que como cabía esperar, es la desviación que experimenta el rayo del luz al refractarse

${\displaystyle \Delta R=\theta -\alpha =\arcsin \left(n\frac{r_0\sin {\varphi }_0}{r}\right)-\arcsin \left(\frac{r_0\sin {\varphi }_0}{r}\right)}$

Trazado de rayos

Establecemos el radio r de la capa en unidades del radio r₀ de la Tierra, el índice n de refracción de la capa.

Establecemos la posición del punto P sobre la capa mediante el ángulo φ que hace la dirección radial con el eje Z y el ángulo del rayo incidente θ respecto de dicha dirección radial. El rayo incidente es el segmento de la recta que pasa por el punto P y forma un ángulo ϕ=φ+θ con el eje Z.

Dado el ángulo de incidencia θ, se calcula el ángulo α de la refracción. El rayo refractado es el segmento de la recta que pasa por el punto P y forma un ángulo ϕ₀=φ+α con el eje Z

Se calcula la intersección del rayo refractado con la superficie de la Tierra (no siempre hay intersección).

${\displaystyle \begin{array}{l}{x}^2+y^2=r^2\\ y=mx+b\end{array}\}{x}_p=\frac{-mb+\sqrt{{\left(mb\right)}^2-\left(m^2+1\right)\left(b^2-r^2\right)}}{m^2+1}}$

El ángulo de refracción ΔR=ϕ-ϕ₀=θ-α como puede comprobarse al correr el código

R=1; %radio de la Tierra
r=1.5; %radio de la capa
n=1.7; %índice de refracción

phi=pi/6; %punto  P, ángulo respecto al eje vertical
th=pi/3; %dirección del rayo de luz,respecto de la dirección radial

%la Tierra y la capa atmosférica
hold on
t=linspace(0,pi,100);
fill(r*cos(t), r*sin(t),'y')
fill(R*cos(t), R*sin(t),[0.7,0.7,0.7]) %color gris claro


x1=r*sin(phi); %punto P en la capa, rayo incidente
y1=r*cos(phi);
plot(x1,y1,'ko','linewidth',1,'markersize',3,'markeredgecolor',
'k','markerfacecolor','k')
cPen_1=phi+th; %ángulo con el eje Z
m=tan(pi/2-cPen_1); % pendiente de la recta
b=y1-m*x1;
fplot(@(x) m*x+b,[x1,x1+2*sin(phi)],'color','r') %rayo incidente
fplot(@(x) m*x+b,[x1-0.5*sin(phi),x1],'color','r','linestyle','--')
fplot(@(x) y1*x/x1,[0,x1+0.5*cos(atan(y1/x1))],'color','k','linestyle','--')

%rayo refractado
alfa=asin(sin(th)/n);
cPen_0=phi+alfa; %ángulo con el eje Z
m=tan(pi/2-cPen_0); %pendiente de la recta
b=y1-m*x1;

%calcula P1 (intersección recta circunferencia de radio R)
x2=(-2*m*b+sqrt((2*m*b)^2-4*(m^2+1)*(b^2-R^2)))/(2*(m^2+1));
x21=(-2*m*b-sqrt((2*m*b)^2-4*(m^2+1)*(b^2-R^2)))/(2*(m^2+1));
y2=m*x2+b;
plot(x2,y2,'ko','linewidth',1,'markersize',3,'markeredgecolor',
'k','markerfacecolor','k')
fplot(@(x) m*x+y1-m*x1,[x2,x1],'color','r')
fplot(@(x) y2*x/x2,[0,x2+0.5*cos(atan(y2/x2))],'color','k','linestyle','--')

hold off
axis equal
axis off
disp('Angulo de refracción')
disp(cPen_1-cPen_0);
disp(th-alfa);

Angulo de refracción
    0.5127
    0.5127

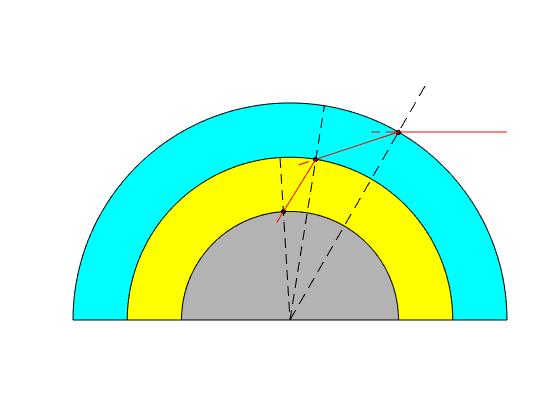
Una atmósfera formada por dos capas

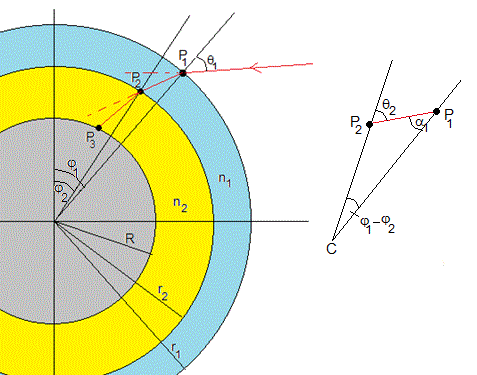
Supongamos que la atmósfera de la Tierra está fomada por dos capas de radios r₁, la exterior, y r₂, la interior. Sus índices de refracción son n₁ y n₂, respectivamente.

Establecemos la posición del punto P₁ sobre la capa externa mediante el ángulo φ₁ que hace la dirección radial con el eje Z y el ángulo del rayo incidente θ₁ respecto de dicha dirección radial. El rayo incidente es el segmento de la recta que pasa por el punto P₁ y forma un ángulo ϕ₁=φ₁+θ₁ con el eje Z.

Dado el ángulo de incidencia θ₁, se calcula el ángulo α₁ de la refracción. El rayo refractado es el segmento de la recta que pasa por el punto P₁ y forma un ángulo ϕ₂=φ₁+α₁ con el eje Z

Se calcula la intersección P₂ del rayo refractado con segunda capa (no siempre hay intersección).

Se calcula el ángulo de incidencia θ₂ que forma el rayo refractado con la dirección radial que pasa por P₂, de acuerdo con los ángulos del triángulo P₁CP₂ a la derecha de la figura θ₂=α₁+(φ₁-φ₂)

Se calcula el ángulo α₂ de la refracción. El rayo refractado es el segmento de la recta que pasa por el punto P₂ y forma un ángulo ϕ₃=φ₂+α₂ con el eje Z

Se calcula la intersección del rayo refractado con la superficie de la Tierra (no siempre hay intersección).

El ángulo de refracción ΔR=ϕ₁-ϕ₃=(θ₁-α₁)+(θ₂-α₂) como puede comprobarse al correr el código

Finalmente, comprobamos que los productos r₁·n₁·sinα₁=r₂·n₂·sinα₂. Una propiedad importante de la trayectoria que sigue el rayo de luz al atravesar la atmósfera, que demostraremos más adelante.

R=1;
r2=1.5; %capa interior
r1=2; %capa exterior
n1=1.3; %índices de refracción
n2=3;

phi_1=pi/6; %punto P1, ángulo con el eje Z
th_1=pi/3; %dirección del rayo de luz, respecto de la dirección radial

%la tierra y las capas 
hold on
t=linspace(0,pi,100);
fill(r1*cos(t), r1*sin(t),'c')
fill(r2*cos(t), r2*sin(t),'y')
fill(R*cos(t), R*sin(t),[0.7,0.7,0.7])

x1=r1*sin(phi_1); %punto P1 en la capa externa
y1=r1*cos(phi_1);
plot(x1,y1,'ko','linewidth',1,'markersize',3,'markeredgecolor',
'k','markerfacecolor','k')
cPen_1=phi_1+th_1; %ángulo con el eje Z
m=tan(pi/2-cPen_1);
b=y1-m*x1;
fplot(@(x) m*x+b,[x1,x1+2*sin(phi_1)],'color','r') %rayo incidente
fplot(@(x) m*x+b,[x1-0.5*sin(phi_1),x1],'color','r','linestyle','--')
fplot(@(x) y1*x/x1,[0,x1+0.5*cos(atan(y1/x1))],'color','k','linestyle','--')

%rayo refractado
alfa_1=asin(sin(th_1)/n1);
cPen_2=phi_1+alfa_1; %ángulo con el eje Z
m=tan(pi/2-cPen_2);
b=y1-m*x1;

%calcula P2 (intersección recta, circunferencia de radio r2)
x2=(-m*b+sqrt((m*b)^2-(m^2+1)*(b^2-r2^2)))/(m^2+1);
x21=(-m*b-sqrt((m*b)^2-(m^2+1)*(b^2-r2^2)))/(m^2+1);
y2=m*x2+b;
phi_2=atan(x2/y2);
plot(x2,y2,'ko','linewidth',1,'markersize',3,'markeredgecolor',
'k','markerfacecolor','k')
fplot(@(x) m*x+y1-m*x1,[x2,x1],'color','r')
fplot(@(x) m*x+y1-m*x1,[x2-1*cos(atan(y2/x2)),x1],'color','r', 'linestyle','--')
fplot(@(x) y2*x/x2,[0,x2+0.5*cos(atan(y2/x2))],'color','k','linestyle','--')

%rayo refractado en P2
th_2=phi_1-phi_2+alfa_1;
alfa_2=asin(n1*sin(th_2)/n2);
cPen_3=phi_2+alfa_2; %ángulo con el eje Z
m=tan(pi/2-cPen_3);
b=y2-m*x2;

%calcula P3 (intersección recta con la circunferencia de radio R, la Tierra)
x3=(-2*m*b+sqrt((2*m*b)^2-4*(m^2+1)*(b^2-R^2)))/(2*(m^2+1));
y3=m*x3+b;
plot(x3,y3,'ko','linewidth',1,'markersize',3,'markeredgecolor',
'k','markerfacecolor','k')
fplot(@(x) m*x+y2-m*x2,[x3,x2],'color','r')
fplot(@(x) m*x+y2-m*x2,[x3-1*cos(atan(y3/x3)),x2],'color','r', 'linestyle','--')
fplot(@(x) y3*x/x3,[x3-0.5*cos(atan(y3/x3)),0],'color','k','linestyle','--')

hold off
axis equal
axis off
disp('Angulo de refracción')
disp(cPen_1-cPen_3)
disp(th_1-alfa_1+th_2-alfa_2)

Angulo de refracción
    1.0165
    1.0165
>> r1*n1*sin(alfa_1)
ans =    1.7321
>> r2*n2*sin(alfa_2)
ans =    1.7321

Observación de un objeto lejano

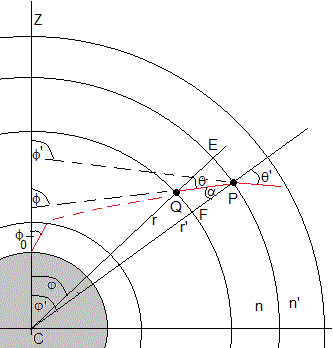
Supongamos que la atmósfera que rodea a la Tierra está formada por capas de índice de refracción n decreciente con la altura. La luz procedente del objeto distante, se propaga por las distintas capas curvándose y llega a la superficie de la Tierra formando la recta tangente a su trayectoria, un ángulo ϕ₀ con el eje vertical Z, ésta es la posición aparente del objeto celeste.

Consideremos dos capas adyacentes de índices de refracción n y n', el rayo que incide en el punto P que forma un ángulo θ' con la dirección radial, se refracta formando un ángulo más pequeño α con dicha dirección radial. La ley de la refracción se escribe, n'sinθ'=nsinα

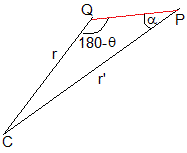
Queremos calcular el ángulo θ del rayo incidente que se refracta en Q. Consideremos el triángulo CPQ, con los radios CP=r' y CQ=r

${\displaystyle \begin{array}{l}\frac{r}{\sin \alpha }=\frac{r\text{'}}{\sin (180-\theta )}\\ r\text{'}\sin \alpha =r\sin \theta \end{array}}$

Eliminamos el ángulo α entre esta ecuación y la de la ley de la refracción, obteniendo una importante relación, n'·r'·sinθ'=n·r·sinθ

El producto de tres términos: el radio r, el índice de refracción n y el seno del ángulo del rayo inicidente θ, es constante a lo largo de la trayectoria que sigue la luz en un medio estratificado formado por capas esféricas.

En la superficie de la Tierra se cumplirá que, n·r·sinθ=n₀·r₀·sinϕ₀. Siendo ϕ₀ el ángulo de observación

El ángulo de refracción

Cuando el rayo se refracta en P el ángulo que forma su prolongación con el eje Z cambia de ϕ' a ϕ, tal como vemos en la figura. El ángulo correspondiente a una única refracción será ΔR=ϕ'-ϕ

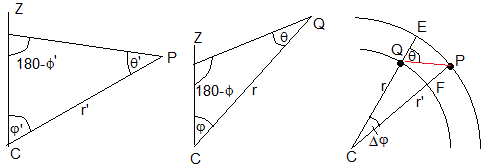
Como vemos en los dos triángulos de la figura, se cumple que ϕ'=φ'+θ' y ϕ=φ+θ. El ángulo de refracción será, ΔR=ϕ'-ϕ=(θ'-θ)+(φ'-φ)=Δθ+Δφ.

Sea Δφ=φ'-φ el ángulo QCF comprendido entre los radios r y r', el arco QF es igual a r·Δφ y el arco EP es igual a r'·Δφ. Llamamos r'=r+Δr, Δr es QE

${\displaystyle \tan \theta =\frac{EP}{QE}=\frac{r\Delta \phi }{\Delta r}}$

Llamando n'=n+Δn (ya que el índice de refracción decrece al incrementarse r) y θ'=θ+Δθ. Como hemos demostrado

${\displaystyle \begin{array}{l}r\text{'}·n\text{'}·\sin \theta \text{'}=n·r·\sin \theta \\ (r+\Delta r)(n-\Delta n)\sin (\theta +\Delta \theta )=n·r·\sin \theta \end{array}}$

Teniendo en cuenta que Δθ es un ángulo pequeño, sin(Δθ)≈Δθ, cos(Δθ)≈1. Como Δr y Δn son también cantidades pequeñas, despreciamos los productos Δn·Δr, Δr·Δθ y Δn·Δθ

${\displaystyle \begin{array}{l}\left(rn+n\Delta r-r\Delta n\right)\left(\sin \theta +\Delta \theta \cos \theta \right)=n·r·\sin \theta \\ rn\sin \theta +rn\cos \theta ·\Delta \theta +n\Delta r\sin \theta -r\Delta n\sin \theta =n·r·\sin \theta \\ rn\cos \theta ·\Delta \theta +n\Delta r\sin \theta -r\Delta n\sin \theta =0\\ \frac{\Delta r}{r}-\frac{\Delta n}{n}+\frac{\Delta \theta }{\tan \theta }=0\end{array}}$

Teniendo en cuenta que tanθ=r·Δφ/Δr o bien, Δr/r=Δφ/tanθ

${\displaystyle \begin{array}{l}\frac{\Delta \phi }{\tan \theta }-\frac{\Delta n}{n}+\frac{\Delta \theta }{\tan \theta }=0\\ \frac{\Delta \phi +\Delta \theta }{\tan \theta }=\frac{\Delta n}{n}\\ \Delta R=\frac{\Delta n}{n}\tan \theta \end{array}}$

Hemos demostrado, n·r·sinθ=n₀·r₀·sinϕ₀

${\displaystyle \begin{array}{l}\Delta R=\frac{\Delta n}{n}\frac{\sin \theta }{\sqrt{1-{\sin }^2\theta }}\\ \Delta R=\frac{\Delta n}{n}\frac{r_0{n}_0\sin {\varphi }_0}{\sqrt{r^2{n}^2-r_0^2{n}_0^2{\sin }^2{\varphi }_0}}\end{array}}$

Esta ecuación determina el ángulo de refracción ΔR experimentado por un rayo de luz cuando pasa de una capa de índice de refracción n-Δn a la siguiente de índice n. El ángulo de refracción R debido a todas las capas de la atmósfera está dado por

${\displaystyle R=r_0{n}_0\sin {\varphi }_0{\displaystyle \underset{1}{\overset{n_0}{\int }}\frac{dn}{n\sqrt{r^2{n}^2-r_0^2{n}_0^2{\sin }^2{\varphi }_0}}}}$

Los límites de integración son, n₀ en la superficie de la Tierra y 1 cuando los gases enrarecidos de la atmósfera no producen efectos ópticos. Para calcular la integral precisamos la relación del índice de refracción n con la distancia r al centro de la Tierra.

En la práctica, se realizan aproximaciones, para obtener una fórmula manejable del ángulo de refracción R en términos del ángulo de observación ϕ₀. La primera aproximación sería la de considerar la altura de la atmósfera pequeña frente al radio r₀ de la Tierra, r=r₀(1+s). Donde s es una cantidad pequeña y se desprecian los términos en s², s³...

Indice de refracción de la atmósfera

Ya hemos estudiado un modelo de atmósfera consistente en una sola capa homogénea de índice de refracción constante, denomominada modelo de Cassini

Newton supuso una atmósfera isotérmica en la que la densidad del aire ρ(r) disminuye exponencialmente con la altura r-r₀. El índice de refracción n(r) del aire sería

${\displaystyle \begin{array}{l}\rho (r)=\rho (r_0)\exp \left(-\frac{r-r_0}{H}\right)\\ n(r)=1+k\frac{\rho (r)}{\rho (r_0)}=1+k\exp \left(-\frac{r-r_0}{H}\right)\end{array}}$

donde k es una constante que determina su valor a nivel del mar r=r₀. Teniendo en cuenta que dn=(dn/dr)dr y llamando x=(r-r₀)/H, la integral se convierte en,

${\displaystyle R=k\sin {\varphi }_0{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{1}{1+k{e}^{-x}}\frac{e^{-x}}{\sqrt{{\left(\frac{\left(1+k{e}^{-x}\right)\left(1+Hx/r_0\right)}{(1+k)}\right)}^2-{\sin }^2{\varphi }_0}}dx}}$

Dibujamos la función integrando, para establecer un límite superior adecuado. Tomamos los valors de k, H y r₀ del segundo artículo citado en las referencias

k=0.000263462;
H=8.59735; %km
r0=6366; % radio dela Tierra, km
phi=(90-3)*pi/180; %ángulo
f=@(x) exp(-x)./((1+k*exp(-x)).*sqrt(((1+k*exp(-x)).*(1+H*x/r0)/(1+k)).^2-
sin(phi)^2));
fplot(f,[0,H])
grid on
xlabel('x')
ylabel('f(x)')
title('Integrando')

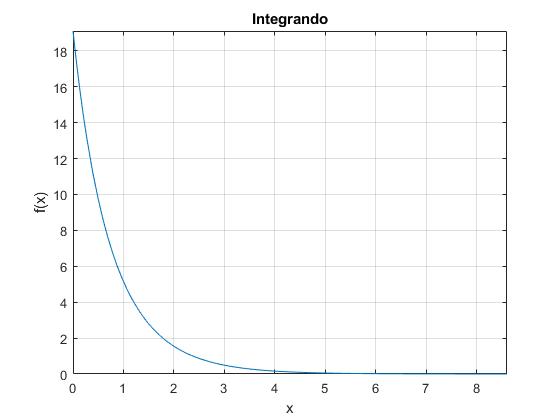
Consideramos que a partir de x=H la función f(x)≈0, se hace casi cero. Tomaremos H=8.6 km como límite superior

Creamos una tabla de ángulos 90°-ϕ₀ (entre 0.5 y 10°) en la primera columna, y de ángulos de refracción R en minutos (segunda columna) y segundos (tercera columna), similar a la de Newton. Véase la tabla I del segundo artículo citado en las referencias

k=0.000263462;
H=8.59735; %km
r0=6366; %km

th=0.5:0.5:10;
disp('ángulo  minutos  segundos')
for phi=(90-th)*pi/180
    f=@(x) exp(-x)./((1+k*exp(-x)).*sqrt(((1+k*exp(-x)).*(1+H*x/r0)/(1+k)).^2
-sin(phi)^2));
    R=k*sin(phi)*integral(f,0,H);
    minutos=floor(R*180*60/pi);
    segundos=round((R*180*60/pi-minutos)*60);
    fprintf('%2.1f       %i        %i\n',(pi/2-phi)*180/pi, minutos, segundos) 
end

ángulo  minutos  segundos
0.5       27        35
1.0       23        7
1.5       19        44
2.0       17        8
2.5       15        5
3.0       13        25
3.5       12        4
4.0       10        56
4.5       9        59
5.0       9        11
5.5       8        29
6.0       7        53
6.5       7        21
7.0       6        53
7.5       6        28
8.0       6        6
8.5       5        46
9.0       5        28
9.5       5        12
10.0      4        57

Principio de Fermat

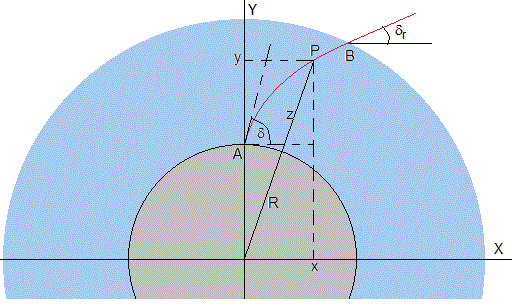
La luz emitida por un objeto S alejado de la Tierra se propaga a lo largo de la recta que forma un ángulo δ_r con la horizontal, penetra en la atmósfera en B donde se refracta y llega a la posición del observador A(0,R) sobre su superficie y forma un ángulo δ con la horizontal.

El dibujo es una exageración de la situación real, en la que el radio de la Tierra supuesta esférica es de 6378 km (radio ecuatorial) y la atmósfera tiene una altura aproximada de 50 km.

El problema que se plantea es la propagación del un rayo de luz por un medio no homogéneo cuyo índice de refracción varía con la altura z del punto P de coordenadas (x,y) sobre la superficie de la Tierra

${\displaystyle z=\sqrt{x^2+y^2}-R}$

El principio de Fermat del tiempo mínimo afirma que

${\displaystyle I={\displaystyle \underset{A}{\overset{B}{\int }}n(z)\sqrt{d{x}^2+d{y}^2}}={\displaystyle \underset{A}{\overset{B}{\int }}n(z)\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}={\displaystyle \underset{A}{\overset{B}{\int }}n(z)\sqrt{1+{\dot{y}}^2}dx}}$

Donde A es el punto de observación (0, R) y B es el punto de intersección de rayo de luz con superficie esférica (circunferencia en el dibujo) de radio R+50 km que señala el límite exterior de la atmósfera. Supondremos que fuera de la atmósfera el rayo de luz se propaga de forma rectilínea, su índice de refracción es constante e igual a la unidad, n=1.

Para que el tiempo sea mínimo, tenemos que calcular el extremo de la funcional

${\displaystyle \begin{array}{l}f(x,y,\dot{y})=n(z)\sqrt{1+{\dot{y}}^2}\\ \frac{\partial f}{\partial y}-\frac{d}{dx}\left(\frac{\partial f}{\partial \dot{y}}\right)=0\end{array}}$

para obtener la ecuación diferencial de la trayectoria

${\displaystyle \begin{array}{l}\frac{\partial f}{\partial y}=\frac{dn}{dz}\frac{\partial z}{dy}\sqrt{1+{\dot{y}}^2}=\frac{dn}{dz}\frac{y}{\sqrt{x^2+y^2}}\sqrt{1+{\dot{y}}^2}\\ \frac{\partial f}{\partial \dot{y}}=n(z)\frac{\dot{y}}{\sqrt{1+{\dot{y}}^2}}\\ \frac{d}{dx}\left(\frac{\partial f}{\partial \dot{y}}\right)=\frac{dn(z)}{dx}\frac{\dot{y}}{\sqrt{1+{\dot{y}}^2}}+n(z)\frac{\ddot{y}}{{\left(1+{\dot{y}}^2\right)}^{3/2}}=\\ \frac{dn}{dz}\frac{dz}{dx}\frac{\dot{y}}{\sqrt{1+{\dot{y}}^2}}+n(z)\frac{\ddot{y}}{{\left(1+{\dot{y}}^2\right)}^{3/2}}=\\ \frac{dn}{dz}\frac{x+y\dot{y}}{\sqrt{x^2+y^2}}\frac{\dot{y}}{\sqrt{1+{\dot{y}}^2}}+n(z)\frac{\ddot{y}}{{\left(1+{\dot{y}}^2\right)}^{3/2}}\end{array}}$

Despejamos d²y/dx²

${\displaystyle \begin{array}{l}\frac{dn}{dz}\frac{y}{\sqrt{x^2+y^2}}\sqrt{1+{\dot{y}}^2}-\frac{dn}{dz}\frac{x+y\dot{y}}{\sqrt{x^2+y^2}}\frac{\dot{y}}{\sqrt{1+{\dot{y}}^2}}-n(z)\frac{\ddot{y}}{{\left(1+{\dot{y}}^2\right)}^{3/2}}=0\\ \{\begin{array}{l}\frac{d^{2}y}{d{x}^2}=\frac{\frac{dn}{dz}}{n(z)}\frac{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}{\sqrt{x^2+y^2}}\left\{y\left(1+{\left(\frac{dy}{dx}\right)}^2\right)-\frac{dy}{dx}\left(x+y\frac{dy}{dx}\right)\right\}\\ z=\sqrt{x^2+y^2}-R\end{array}\end{array}}$

Esta es la ecuación diferencial de la trayectoria

Indice de refracción de la atmósfera

En la página titulada Modelos simples de atmósfera se estudia los modelos de atmósfera isotermos y aquellos en los que la temperatura disminuye linealmente con la altura.

En la página web de la NASA (National Aeronautics and Space Administration) titulada Earth Atmosphere model se describe un modelo de atmósfera que consta de tres capas. La altura z se da en metros, la temperatura T en gardos centígrados y la presión p en kPa

• Por debajo de 11000 m de altura. La temperatura disminuye linealmente y la presión disminuye

T=15.04-0.00649·z
p=101.29·[(T+273.1)/288.08]^5.256

• De 11000 m a 25000 m de altura. La temperatura es constante y la presión disminuye exponencialmente

T=-56.46
p=22.65·exp(1.73-0.000157·z)

• Por encima 25000 m de altura. La temperatura aumenta ligeramente y la presión disminuye

T=-131.21+0.00299 ·z
p=2.488·[(T+273.1)/216.6]^-11.388

Buscamos una expresión sencilla del índice de refración n del aire en términos de la presión p y la temperatura T

${\displaystyle n=1+7.93643·{10}^{-4}\frac{p}{T}}$

donde p se mide en kPa y T en K.

Representamos el índice de refracción n en función de la altura z en km

z=0:100:50000; %altura hasta 50 km
zona1=z<
zona2=z>=11000 & z<25000;
zona3=z>=25000;

T=zona1.*(15.04-0.00649*z)+zona2.*(-56.46)+zona3.*(-131.21+0.00299*z);
p=zona1.*(101.29*((T.*zona1+273.1)/288.08).^5.256)+zona2.*
(22.65*exp(1.73-.000157*z.*zona2))+zona3.*(2.488*((T.*zona3+273.1)/216.6).^-11.388);
n=1+7.9364e-04*p./(T+273.1);
plot(z/1000,n)
grid on
xlabel('z (km)')
ylabel('n')
title('Indice de refracción')

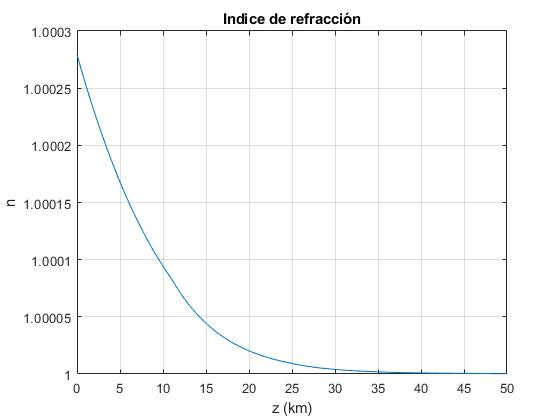
El índice de refracción n cambia muy poco con la altura z

Trayectoria y ángulos de desviación

Integramos la ecuación diferencial con las siguientes condiciones iniciales, en la posición del observador, x=0, y=R, la luz parte con un ángulo δ respecto de la horizontal, dy/dx=tanδ y sale de la atmósfera formando un ángulo δ_r, moviénde después en una trayectoria rectilínea. Vamos a representar la trayectoria de un rayo de luz en la atmósfera y a calcular la diferencia δ-δ_r en función de δ

Definimos una función que interrumpe el proceso de integración cuando el rayo de luz sale de la atmósfera.

function [value,isterminal,direction]=stop_atmosfera(t,x)
    z=sqrt(x(1)^2+t^2)-6370;  %y es x(1), x es t, z es la distancia radial
    value=z-50;
    isterminal=1; %1 detiene la integración cuando la velocidad se hace cero   
    direction=0; % 1 crece, -1 decrece, 0 no importa
end

Definimos la función a integrar de acuerdo con el modelo de atmósfera y la relación entre el índice de refracción n con la presión p y la temperatura T. Conocida la expresión de n(z), también tenemos que calcular la derivada, dn/dz

function dr = refraccion_atm(t,x)
  z=sqrt(x(1)^2+t^2)*1000-6370*1000;  %y es x(1), x es t, z es la distancia radial
  if z<11000
        T=15.04-0.00649*z+273.1;
        p=101.29*(T/288.08)^5.256;
        dp=-0.006497*101.29*5.256*T^4.256/288.08^5.256; %derivada dp/dz
        dT=-0.00649; %derivada dT/dz
  elseif z>11000 && z<25000   
       T=-56.46+273.1;
       p=22.65*exp(1.73-0.000157*z);
       dT=0; %derivada dT/dz
       dp=-25.65*0.000157*exp(1.73-0.000157*z); %derivada dp/dz
  else
       T=-131.21+0.00299*z+273.1;
       p=2.488*(T/216.6)^-11.388;
       dT=0.00299; %derivada dT/dz
       dp=-0.00299*2.488*11.388*T^-12.388/216.6^-11.388; %derivada dp/dz
    end
    n=1+7.9364e-04*p/T; %n(z)
    dn=(dp*T-p*dT)/T^2; % derivada dn/dz
    dr=zeros(2,1);
    dr(1)=x(2);
    dr(2)=dn*(1+x(2)^2)*(x(1)*(1+x(2)^2)-x(2)*(x(1)*x(2)+t))/(n*sqrt(x(1)^2+t^2));
end

Representamos la trayectoria del rayo de luz en la atmósfera, hasta 50 km de altura

th=10; %ángulo, grados
opts=odeset('events',@stop_atmosfera);
[t,x]=ode45(@refraccion_atm,[0,1000],[6378, tan(th*pi/180)], opts);
plot(t,x(:,1))
grid on
xlabel('x (km)')
ylabel('y (km)');
title('Trayectoria')

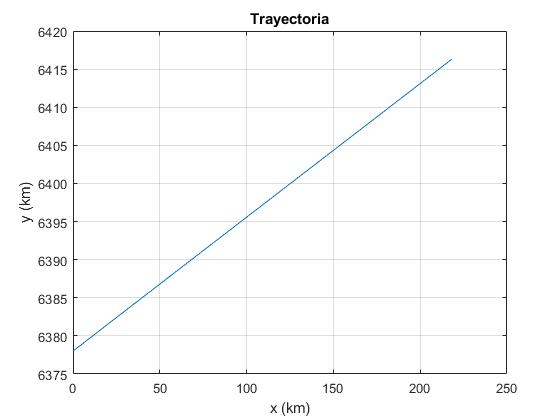
Vemos que la trayectoria es casi rectilínea, que la diferencia entre el ángulo inicial δ y el ángulo final δ_r es muy pequeña, 0.0531 grados ó 3.2 min de arco. El procedimiento numérico debe ser muy estable para que las diferencias sean tan pequeñas a tan grandes distancias. Por lo que no podemos estar seguros de que los resultados sean correctos

>>  th-atan(x(end,2))*180/pi
ans =    0.0531
>> ans*60
ans =    3.1861

Representamos la diferencia δ-δ_r en función de δ

ang=linspace(0,20,100);
ang_r=zeros(1,length(ang));
i=1;
opts=odeset('events',@stop_atmosfera);
for th=ang
    [t,x]=ode45(@refraccion_atm, [0,1000],[6378,tan(th*pi/180)], opts);
    ang_r(i)=(th-atan(x(end,2))*180/pi)*60; %en minutos
    i=i+1;
end
plot(ang,ang_r)
grid on
xlabel('\delta (grad)')
ylabel('\delta-\delta_r (min)');
title('Refracción atmosférica')

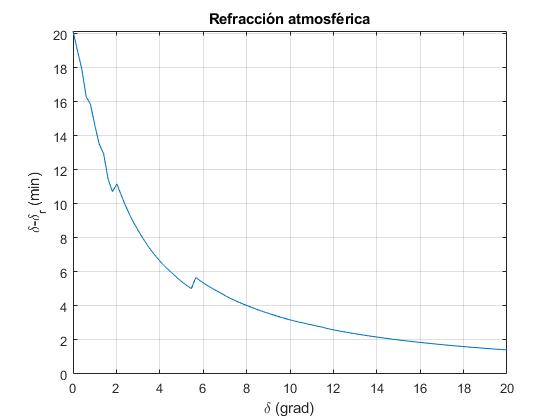
Esta diferencia de ángulos explica la forma ovalada del Sol o de la Luna cuando están cercanos al horizonte. Su diámetro vertical disminuye por efecto de la refracción atmosférica.

Obtenemos una representación gráfica, similar a la figura 6, del tercer artículo mencionado a las referencias, ese artículo utiliza un modelo distinto de atmósfera (dos capas). Las líneas quebradas para ángulos δ pequeños indican que el procedimiento numérico podría fallar para ciertos ángulos. Así pues, hemos probado el procedimiento ode45 de MATLAB en una situación límite.

Referencias

W. M. Smart, R. M. Green. Textbook on Spherical Astronomy, 6th edition. Cambridge University Press (1977), chapter III, Refraction. 58-65

Michael Nauenberg. Newton's theory of the atmospheric refraction of light. Am. J. Phys. 85 (12) December 2017, 921-925

Z. Néda, S. Volkán. Flatness of the setting Sun. https://arxiv.org/abs/physics/0204060v1. Submitted on 19 Apr 2002