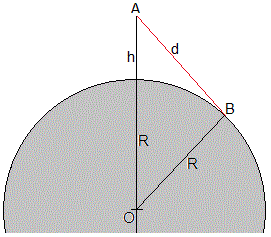
Supongamos que la Tierra no tiene atmósfera, la luz se propaga a lo largo de una línea recta. El observador está en A a una altura h sobre la superficie de la Tierra. Trazamos la línea AB tangente a la superficie terrestre en B y que pasa por A. En el triángulo rectángulo OBA

${\displaystyle \begin{array}{l}{\left(R+h\right)}^2=R^2+d^2\\ d^2=h\left(2R+h\right)\\ d\approx \sqrt{2Rh},h\ll R\end{array}}$

Sabiendo que el radio de la Tierra R=6371 km.

• una persona que está de pié en la playa, sus ojos a h=2 m del suelo, la distancia al horizonte d=5.05 km
• una persona situada en la cima de una montaña cercana al mar de altura h=1000 m, la distancia al horizonte d=112.88 km

Corrección debido a la refracción de la atmósfera

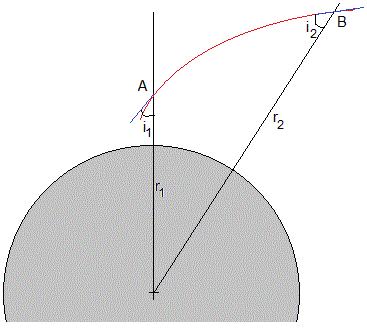
El problema no es sencillo si se tiene en cuenta el hecho de que la atmósfera es un medio cuyo índice de refracción disminuye con la altura. La trayectoria del rayo de luz ya no es rectilínea sino una curva cóncava hacia la superficie de la Tierra.

En la página titulada 'Refracción en la atmósfera', demostramos una importante relación de la óptica atmosférica

n₁r₁·sini₁=n₂r₂·sini₂=constante

La línea de color rojo, es la trayectoria seguida por el rayo de luz. Los ángulos que forman las tangentes a dicha trayectoria en A y B con la dirección radial son los ángulos de incidencia i₁ e i₂. Los índices de refracción de la atmósfera en las posiciones A y B son n₁ y n₂, respectivamente

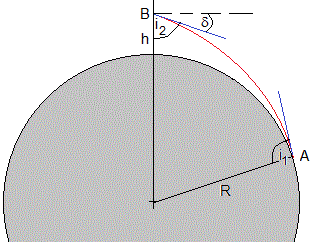
En la situación que estudiamos, el rayo de luz parte de un punto A en la superficie de la Tierra y llega al observador situado en B a una altura h

Como apreciamos en la figura

• En el punto A, r₁=R y i₁=90°. El índice de refracción es n₀ a nivel del mar
• En el punto B, r₂=R+h. El índice de refracción es n=n₀+Δn

Utilizamos la aproximación (1+x)^-1≈1-x, para x<<1.

>> syms x;
>> taylor(1/(1+x),x) 
ans =- x^5 + x^4 - x^3 + x^2 - x + 1 

${\displaystyle \begin{array}{l}n(R+h)\sin i_2=n_{0}R\sin i_1\\ \sin i_2=\frac{n_{0}R}{\left(n_0+\Delta n\right)\left(R+h\right)}={\left(1+\frac{\Delta n}{n_0}\right)}^{-1}{\left(1+\frac{h}{R}\right)}^{-1}\\ \sin i_2\simeq 1-\frac{\Delta n}{n_0}-\frac{h}{R}\end{array}}$

Los ángulo i₂ y δ son complementarios, sinδ=cosi₂. Teniendo en cuenta que el ángulo δ es pequeño, sinδ≈δ

${\displaystyle \delta \simeq \sqrt{1-{\sin }^2{i}_2}\simeq \sqrt{2\frac{\Delta n}{n_0}+2\frac{h}{R}}=\sqrt{2\frac{h}{R}}\sqrt{1+\frac{R}{h}\frac{\Delta n}{n_0}}\simeq \sqrt{2\frac{h}{R}}\left(1+\frac{R}{2h}\frac{\Delta n}{n_0}\right)}$

Utilizamos la aproximación (1+x)^1/2≈1+x/2, para x<<1.

>> syms x;
>> taylor(sqrt(1+x),x)
ans =(7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + x/2 + 1

Cuando el efecto de la atmósfera es despreciable

${\displaystyle \delta \simeq \sqrt{2\frac{h}{R}}}$

tal como puede deducirse a partir de la primera figura, suponiendo que h<<R

Indice de refracción

En la página titulada 'Refracción en la atmósfera', proporcionamos una expresión para el valor del índice de refracción n(r) con la distancia radial

${\displaystyle \begin{array}{l}n(r)=1+k\exp \left(-\frac{r-R}{H}\right)\\ n(z)=1+k\exp \left(-\alpha z\right)\end{array}}$

donde z es la altura sobre el nivel del mar

Los valores de los parámetros α y k que proporciona el artículo que se menciona en las referencias son k=2.77·10^-4, α=0.105 km^-1

${\displaystyle \Delta n(z)=n(z)-n_0=1+k\exp \left(-\alpha z\right)-(1+k)=-k\left(1-\exp \left(-\alpha z\right)\right)}$

Para alturas z<1 km, αz es pequeño, utilizamos la aproximación, 1-exp(-x)≈x, para x<<1

>> syms x;
>> taylor(1-exp(-x),x)
ans =x^5/120 - x^4/24 + x^3/6 - x^2/2 + x

${\displaystyle \begin{array}{l}\delta \simeq \sqrt{2\frac{h}{R}}\left(1-\frac{R}{2h}\frac{k\left(1-\exp \left(-\alpha h\right)\right)}{1+k}\right)\simeq \sqrt{2\frac{h}{R}}\left(1-\frac{R}{2}k\alpha \right)\\ \delta \simeq (1-0.092)\sqrt{2\frac{h}{R}}\end{array}}$

El factor de corrección para el ángulo δ es 1-0.092 cuando tenemos en cuenta la influencia de la atmósfera

Distancia al horizonte

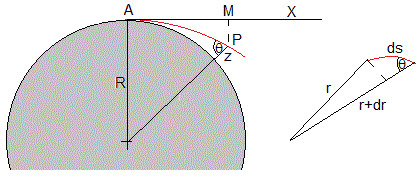
Consideremos el rayo de luz que parte de A. En el punto P de su trayectoria de altura z se cumple que

• En el punto A, el índice de refracción es n₀ a nivel del mar
• En el punto P, r=R+z, la tengente a la trayectoria hace un ángulo θ con la dirección radial. El índice de refracción es n=n₀+Δn

A la derecha, en la figura

${\displaystyle \cos \theta =\frac{dr}{ds}\simeq \frac{dz}{dx}}$

dr=dz, y dx≈ds, ya que la distancia AP es aproximadamente igual a AM.

Hacemos las mismas aproximaciones que en el apartado anterior, sustituyendo la altura final h del punto B por la altura z del punto genérico P.

${\displaystyle \begin{array}{l}\sin \theta =\frac{n_{0}R}{\left(n_0+\Delta n\right)\left(R+z\right)}={\left(1+\frac{\Delta n}{n_0}\right)}^{-1}{\left(1+\frac{z}{R}\right)}^{-1}\simeq 1-\frac{\Delta n}{n_0}-\frac{z}{R}\\ \cos \theta =\sqrt{1-{\sin }^2\theta }\simeq \sqrt{2\frac{\Delta n}{n_0}+2\frac{z}{R}}\end{array}}$

La distancia al horizonte d(h) es

${\displaystyle \begin{array}{l}\frac{dz}{dx}=\sqrt{2\frac{z}{R}}\sqrt{1+\frac{R}{z}\frac{\Delta n}{n_0}}\\ dx=\sqrt{\frac{R}{2z}}{\left(1+\frac{R}{z}\frac{n(z)-n_0}{n_0}\right)}^{-1/2}dz\\ d(h)=\sqrt{\frac{R}{2}}{\displaystyle \underset{0}{\overset{h}{\int }}{\left\{z\left(1+\frac{R}{z}\frac{n(z)-n_0}{n_0}\right)\right\}}^{-1/2}dz}\\ d(h)=\sqrt{\frac{R}{2}}{\displaystyle \underset{0}{\overset{h}{\int }}{\left(z-R\frac{k}{1+k}\left(1-\exp \left(-\alpha z\right)\right)\right)}^{-1/2}dz}\end{array}}$

Esta integral se puede resolver de forma numérica, empleando la función integral de MATLAB

Otras aproximaciones

La raíz cuadrada se aproxima (véase el apartado anterior)

${\displaystyle \begin{array}{l}dx\simeq \sqrt{\frac{R}{2z}}\left(1-\frac{R}{2z}\frac{\Delta n}{n_0}\right)dz\\ d(h)\simeq \sqrt{\frac{R}{2}}{\displaystyle \underset{0}{\overset{h}{\int }}{z}^{-1/2}\left(1-\frac{R}{2z}\frac{n(z)-n_0}{n_0}\right)dz}\end{array}}$

El índice de refracción también se puede aproximar

${\displaystyle n(z)-n_0=1+k\exp \left(-\alpha z\right)-(1+k)=-k\left(1-\exp \left(-\alpha z\right)\right)\simeq -k\alpha z}$

Con esta aproximación, la integral es inmediata

${\displaystyle \begin{array}{l}d(h)\simeq \sqrt{\frac{R}{2}}\left(1+\frac{R}{2}k\alpha \right){\displaystyle \underset{0}{\overset{h}{\int }}{z}^{-1/2}dz}\\ d(h)\simeq \sqrt{2Rh}\left(1+\frac{R}{2}k\alpha \right)=\sqrt{2Rh}\left(1+0.092\right)=123.34\sqrt{h}\end{array}}$

donde la altura h y la distancia al horizonte d (h) se miden en km.

Esta aproximación es válida cuando la altura del observador es menor que 1 km por encima del nivel del mar. Para otras alturas, el error no es muy grande.

La mayor incentidumbre proviene de los valores de los parámetros k y α que dependen de la temperatura y otros factores

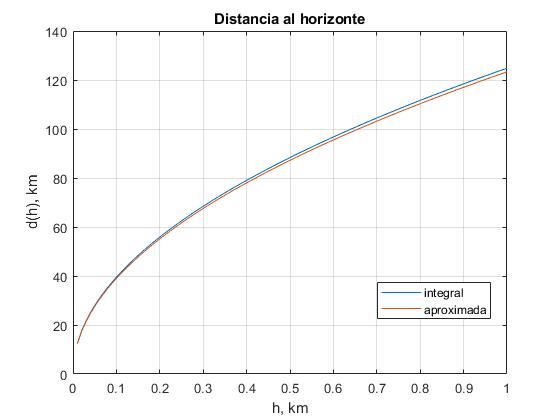
Comparamos la solución más exacta y la aproximada hasta la altura de 1 km, apreciamos que son casi indistinguibles

R=6371; %radio de la Tierra, en km
alfa=0.105; %en km^-1
k=2.77e-4; %parámetro
f=@(x) 1./sqrt(x-R*k*(1-exp(-alfa*x))/(1+k));
hh=(10:10:1000)/1000;
dist=zeros(1,length(hh));
i=1;
for h=hh
    dist(i)=integral(f,0,h)*sqrt(R/2); %más exacta
    i=i+1;
end
dist_a=sqrt(2*R)*(1+R*k*alfa/2)*sqrt(hh); %aproximada
plot(hh,dist, hh,dist_a)
grid on
legend('integral','aproximada','location','best')
xlabel('h, km')
ylabel('d(h), km')
title('Distancia al horizonte')

Referencias

A. P. French. How far is the horizon?. Am. J. Phys. 50 (9) Sept. 1982, pp. 795-799