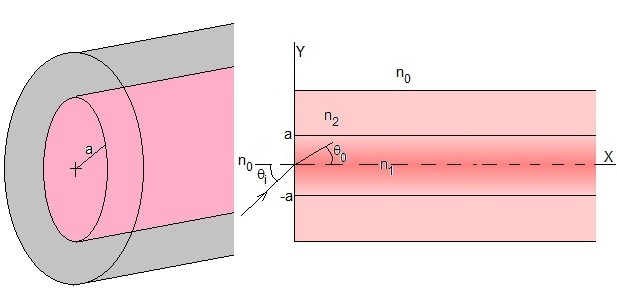
Una fibra óptica consta de un cilindro de radio a hecho de un material transparente cuyo índice de refracción varía radialmente de n₁ en el eje a n₂ a una distancia a del eje, es el núcleo de la fibra. El cilindro está recubierto por una capa cilíndrica de índice de refracción constante n₂. El índice de refracción del aire es n₀≈1

Un rayo de luz incide en el origen formando un ángulo θ_i con el eje X de la fibra. El rayo se refracta y forma un ángulo θ₀ con el eje de la fibra.

${\displaystyle n_0\sin {\theta }_i=n_1\sin {\theta }_0}$

A partir de esta posición (el origen) vamos a determinar el camino que sigue el rayo de luz en el núcleo de la fibra (cilindro de radio a) sabiendo que el índice de refracción varía radialmente, de la forma

${\displaystyle n(y)=n_1\sqrt{1-{\alpha }^2{y}^2},n_1>n_2>1}$

donde y es la distancia desde el eje y α es una constante tal que, el índice de refracción es n₂ para y=a

${\displaystyle \begin{array}{l}{n}_2=n_1\sqrt{1-{\alpha }^2{a}^2}\\ \alpha =\frac{1}{n_{1}a}\sqrt{n_1^2-n_2^2}\end{array}}$

El camino que sigue la luz

En la página titulada 'Propagación en un medio no homogéneo' obtuvimos la ecuación diferencial del camino de la luz cuando el índice de refracción varía con y.

${\displaystyle {\left(\frac{dy}{dx}\right)}^2=\frac{n^2}{n_1^2}\left(1+{\left(\frac{dy}{dx}\right)}_0^2\right)-1}$

La derivada en el origen

${\displaystyle {\left(\frac{dy}{dx}\right)}_0=\tan {\theta }_0}$

El ángulo θ₀ es conocido por la aplicación de la ley de la refracción en el origen

${\displaystyle \begin{array}{l}{\left(\frac{dy}{dx}\right)}^2=\left(1-{\alpha }^2{y}^2\right)\left(1+{\tan }^2{\theta }_0\right)-1\\ {\left(\frac{dy}{dx}\right)}^2=\left(1-{\alpha }^2{y}^2\right)\frac{1}{{\cos }^2{\theta }_0}-1\\ {\left(\frac{dy}{dx}\right)}^2={\tan }^2{\theta }_0-\frac{{\alpha }^2}{{\cos }^2{\theta }_0}{y}^2\end{array}}$

Integramos la ecuación diferencial sabiendo que el camino de la luz pasa por el origen x=0, y=0

${\displaystyle {\displaystyle \underset{0}{\overset{y}{\int }}\frac{dy}{\sqrt{{\tan }^2{\theta }_0-\frac{{\alpha }^2}{{\cos }^2{\theta }_0}{y}^2}}}={\displaystyle \underset{0}{\overset{x}{\int }}dx}}$

El resultado es

${\displaystyle \begin{array}{l}\frac{\cos {\theta }_0}{\alpha }\arcsin \left(\frac{\alpha y}{\sin {\theta }_0}\right)=x\\ y=\frac{\sin {\theta }_0}{\alpha }\sin \left(\frac{\alpha }{\cos {\theta }_0}x\right)\end{array}}$

Introduciendo las expresiones de α y θ₀ (ley de la refracción)

${\displaystyle \begin{array}{l}\frac{y}{a}=\frac{n_0\sin {\theta }_i}{\sqrt{n_1^2-n_2^2}}\sin \left(\sqrt{\frac{n_1^2-n_2^2}{n_1^2-n_0^2{\sin }^2{\theta }_i}}\frac{x}{a}\right)\\ y=A\sin \left(kx\right),A=\frac{n_0\sin {\theta }_i}{\sqrt{n_1^2-n_2^2}}a=\frac{n_1\sin {\theta }_0}{\sqrt{n_1^2-n_2^2}}a,k=\frac{1}{a}\sqrt{\frac{n_1^2-n_2^2}{n_1^2-n_0^2{\sin }^2{\theta }_i}}\end{array}}$

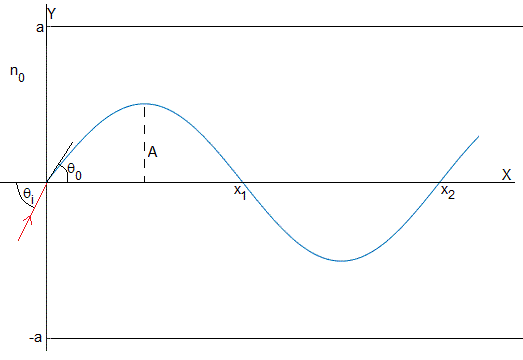
Para que la luz se propague a lo largo del núcleo de la fibra, se tiene que cumplir que y<a, A<a . El ángulo de incidencia máximo, con A=a es

${\displaystyle \sin {\theta }_{im}=\frac{1}{n_0}\sqrt{n_1^2-n_2^2}}$

Con los datos, n₀=1, n₁=1.5 y n₂=1.46

θ_im=20.13°, por tanto, el ángulo de incidencia ha de cumplir θ_i<θ_im

Las posiciones x para las cuales y=0, son

${\displaystyle \begin{array}{l}kx=m\pi ,,m=\mathrm{1,2,3...}\\ x_1=\pi a\sqrt{\frac{n_1^2-n_0^2{\sin }^2{\theta }_i}{n_1^2-n_2^2}},x_2=2x_1,x_3=3x_1\mathrm{,...}\end{array}}$

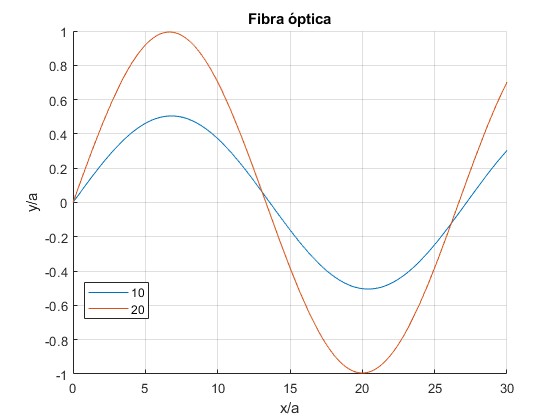
Para θ_i=20°, y es nulo, para x/a= 13.33, 26,67, 40.00, 53.33

Representamos y/a en función de x/a para dos ángulos θ_i, 10° y 20°, tomando n₀=1, n₁=1.5 y n₂=1.46

n0=1;
n1=1.5;
n2=1.46;
hold on
for th=[10,20]*pi/180
    A=n0*sin(th)/sqrt(n1^2-n2^2);
    k=sqrt((n1^2-n2^2)/(n1^2-n0^2*sin(th)^2));
    fplot(@(x) A*sin(k*x),[0,30])
end
hold off
grid on
xlabel('x/a')
legend('10','20','location','best')
ylabel('y/a')
title('Fibra óptica')

Velocidad de propagación

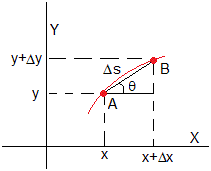
El tiempo dt que tarda la luz en desplazarse desde A hasta B es

${\displaystyle dt=\frac{ds}{v}=\frac{c}{v}\frac{ds}{c}=\frac{n}{c}ds}$

Como apreciamos en la figura

${\displaystyle \Delta s=\sqrt{{\left(\Delta x\right)}^2+{\left(\Delta y\right)}^2}=\sqrt{1+\frac{1}{{\left(\frac{\Delta y}{\Delta x}\right)}^2}}\Delta y}$

En el límite cuando Δx→0

${\displaystyle ds=\sqrt{1+\frac{1}{{\left(\frac{dy}{dx}\right)}^2}}dy}$

El tiempo que tarda la luz en desplazarse ds, es

${\displaystyle \begin{array}{l}dt=\frac{n}{c}ds=\frac{n}{c}\sqrt{1+\frac{1}{{\left(\frac{dy}{dx}\right)}^2}}dy\\ \{\begin{array}{l}n=n_1\sqrt{1-{\alpha }^2{y}^2}\\ {\left(\frac{dy}{dx}\right)}^2=\frac{1-{\alpha }^2{y}^2}{{\cos }^2{\theta }_0}-1\end{array}\\ dt=\frac{n_1}{c}\frac{1-{\alpha }^2{y}^2}{\sqrt{{\sin }^2{\theta }_0-{\alpha }^2{y}^2}}dy\end{array}}$

El tiempo que tarda desde que sale (en el origen) hasta que cruza el eje X (posición x₁), es el doble del tiempo que tarda en desplzarse desde el origen hasta el punto (x₁/2,A). Integramos

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{P/2}{\int }}dt}=\frac{n_1}{c}{\displaystyle \underset{0}{\overset{A}{\int }}\frac{1-{\alpha }^2{y}^2}{\sqrt{{\sin }^2{\theta }_0-{\alpha }^2{y}^2}}dy}\\ \frac{P}{2}=\frac{n_1}{c}\left\{\frac{1}{\alpha }{\displaystyle \underset{0}{\overset{A}{\int }}\frac{1}{\sqrt{\frac{{\sin }^2{\theta }_0}{{\alpha }^2}-y^2}}dy}-\alpha {\displaystyle \underset{0}{\overset{A}{\int }}\frac{y^2}{\sqrt{\frac{{\sin }^2{\theta }_0}{{\alpha }^2}-y^2}}dy}\right\}\end{array}}$

La primera integral es inmediata

${\displaystyle \frac{1}{\alpha }{\displaystyle \int \frac{1}{\sqrt{\frac{{\sin }^2{\theta }_0}{{\alpha }^2}-y^2}}dy}=\frac{1}{\alpha }\arcsin \left(\frac{\alpha y}{\sin {\theta }_0}\right)}$

Integramos par partes la segunda integral

${\displaystyle \begin{array}{l}\alpha {\displaystyle \int \frac{y^2}{\sqrt{\frac{{\sin }^2{\theta }_0}{{\alpha }^2}-y^2}}dy},\{\begin{array}{l}u=y,du=dy\\ dv=-\frac{1}{2}\frac{-2ydy}{\sqrt{\frac{{\sin }^2{\theta }_0}{{\alpha }^2}-y^2}},v=-\end{array}\sqrt{\frac{{\sin }^2{\theta }_0}{{\alpha }^2}-y^2}\\ \alpha \left\{-y\sqrt{\frac{{\sin }^2{\theta }_0}{{\alpha }^2}-y^2}+{\displaystyle \int \sqrt{\frac{{\sin }^2{\theta }_0}{{\alpha }^2}-y^2}dy}\right\}\end{array}}$

Para resolver la inetgral, hacemos un cambio de variable

${\displaystyle \begin{array}{l}y=\frac{\sin {\theta }_0}{\alpha }\sin t,dy=\frac{\sin {\theta }_0}{\alpha }\cos t·dt\\ {\displaystyle \int \sqrt{\frac{{\sin }^2{\theta }_0}{{\alpha }^2}-y^2}dy}=\frac{{\sin }^2{\theta }_0}{{\alpha }^2}{\displaystyle \int {\cos }^{2}t·dt=}\frac{{\sin }^2{\theta }_0}{2{\alpha }^2}{\displaystyle \int \left(1+\cos (2t)\right)·dt=}\frac{{\sin }^2{\theta }_0}{2{\alpha }^2}\left(t+\frac{1}{2}\sin (2t)\right)=\\ \frac{{\sin }^2{\theta }_0}{2{\alpha }^2}\left\{\arcsin \left(\frac{\alpha y}{\sin {\theta }_0}\right)+\frac{\alpha y}{\sin {\theta }_0}\sqrt{1-{\left(\frac{\alpha y}{\sin {\theta }_0}\right)}^2}\right\}\end{array}}$

Evaluamos el integrando entre los límites 0 y A y teniendo en cuenta que αA/sinθ₀=1, el resultado final se simplifica notablemente

${\displaystyle \begin{array}{l}\frac{1}{\alpha }\arcsin \left(\frac{\alpha y}{\sin {\theta }_0}\right)-\alpha {\left\{-y\sqrt{\frac{{\sin }^2{\theta }_0}{{\alpha }^2}-y^2}+\frac{{\sin }^2{\theta }_0}{2{\alpha }^2}\left\{\arcsin \left(\frac{\alpha y}{\sin {\theta }_0}\right)+\frac{\alpha y}{\sin {\theta }_0}\sqrt{1-{\left(\frac{\alpha y}{\sin {\theta }_0}\right)}^2}\right\}\right\}}_0^A\\ =\frac{1}{\alpha }\arcsin \left(\frac{\alpha A}{\sin {\theta }_0}\right)-\alpha \left\{-A\sqrt{\frac{{\sin }^2{\theta }_0}{{\alpha }^2}-A^2}+\frac{{\sin }^2{\theta }_0}{2{\alpha }^2}\left\{\arcsin \left(\frac{\alpha A}{\sin {\theta }_0}\right)+\frac{\alpha A}{\sin {\theta }_0}\sqrt{1-{\left(\frac{\alpha A}{\sin {\theta }_0}\right)}^2}\right\}\right\}=\\ \frac{1}{\alpha }\frac{\pi }{2}-\alpha \left\{\frac{{\sin }^2{\theta }_0}{2{\alpha }^2}\frac{\pi }{2}\right\}=\frac{1}{\alpha }\frac{\pi }{2}-\frac{{\sin }^2{\theta }_0}{2\alpha }\frac{\pi }{2}\end{array}}$

El resultado final es

${\displaystyle \begin{array}{l}\frac{P}{2}=\frac{n_1}{c}\frac{1}{\alpha }\frac{\pi }{2}\left\{1-\frac{{\sin }^2{\theta }_0}{2}\right\}\\ P=\frac{\pi n_1^{2}a}{c\sqrt{n_1^2-n_2^2}}\left\{1-\frac{{\sin }^2{\theta }_i}{2n_1^2}\right\}\end{array}}$

La velocidad de la luz a lo largo la fibra es el cociente entre el desplazamiento horizontal x₁ y el tiempo P que tarda en desplazarse

${\displaystyle v=\frac{x_1}{P}=\frac{\pi a\sqrt{\frac{n_1^2-n_0^2{\sin }^2{\theta }_i}{n_1^2-n_2^2}}}{\frac{\pi n_1^{2}a}{c\sqrt{n_1^2-n_2^2}}\left\{1-\frac{{\sin }^2{\theta }_i}{2n_1^2}\right\}}=\frac{c\sqrt{n_1^2-n_0^2{\sin }^2{\theta }_i}}{n_1^2\left\{1-\frac{{\sin }^2{\theta }_i}{2n_1^2}\right\}}}$

• Para el ángulo de incidencia máximo, θ_im

${\displaystyle v_m=\frac{c\sqrt{n_1^2-\left(n_1^2-n_2^2\right)}}{n_1^2\left\{1-\frac{n_1^2-n_2^2}{2n_1^2{n}_0^2}\right\}}=\frac{2c{n}_2{n}_0^2}{2n_1^2{n}_0^2-n_1^2+n_2^2}=\frac{2c{n}_2}{n_1^2+n_2^2}}$

donde n₀=1, es el índice de refracción del aire

Sabiendo que la velocidad de la luz en el vacío es c=2.9979·10⁸ m/s, con los datos de n₀=1, n₁=1.5 y n₂=1.46, obtenemos v_m=1.9979·10⁸ m/s

• Velocidad de propagación a lo largo del eje del cilindro, eje X, angulo de incidencia θ_i=0

v₀=c/n₁=1.9986·10⁸ m/s

Los rayos con diferentes ángulos de incidencia θ_i tienen distintas velocidades de propagación. Llegan a una posición x en el eje de la fibra en distintos tiempos

Por ejemplo, los rayos cuyo ángulo de incidencia es θ_i=0 y θ_i=θ_im llegan a x con una diferencia de tiempos

${\displaystyle \Delta t=\frac{x}{v_m}-\frac{x}{v_0}=\frac{x}{c}\left(\frac{n_1^2+n_2^2}{2n_2}-n_1\right)=\frac{x}{c}\frac{{\left(n_1-n_2\right)}^2}{2n_2}}$

Un pulso de duración muy pequeña se convierte en un pulso de anchura finita Δt. Si dos pulsos consecutivos entran en la fibra óptica con una separación mayor que Δt entonces se podrán detectar al final de la fibra de forma separada

Para una fibra de longitud x=1000 m

Δt=1.8278·10^-9 s, o una frecuencia límite 1/Δt= 547.1 MHz

Referencias

Asian Physics. (1st – 8th). Olympiad. Problems and Solutions. Editor Zheng Yongling. World Scientific (2010), pp. 129-136