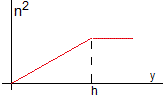
El índice de refracción se incrementa con la altura

En este modelo simple, consideramos que el índice de refracción se incrementa con la altura y hasta una altura h y luego, permenece constante. Corresponde al aire que está sobre una superficie caliente. En la página titulada Espejismos (II) estudiaremos un modelo más complicado

${\displaystyle n^2(y)=\{\begin{array}{l}{n}_0^2+ky,0\le y<h\\ n_0^2+kh,y\ge h\end{array}}$

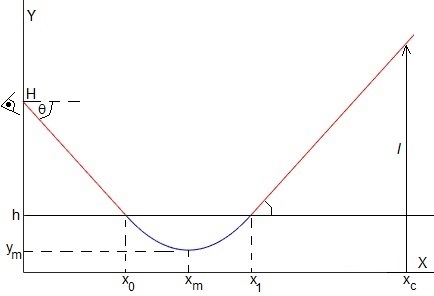
En la figura representamos el camino seguido por la luz desde el extermo del objeto situado en (x_c , l), flecha a la derecha, hasta el observador situado en (0, H). Demostraremos que el camino se compone de una recta, una parábola y otra recta, de la misma pendiente cambiada de signo

La luz procedente del extremo del objeto, le llega al observador haciendo un ángulo -θ con la horizontal.

• y>h. Camino rectilíneo

Como el índice de refracción es constante para y>h, el camino que sigue la luz es una línea recta desde el observador hasta el punto (x₀,h)

${\displaystyle x_0=\frac{H-h}{\tan \theta }}$

• 0≤y≤h. Camino parabólico

Vamos a determinar el camino que sigue la luz en la región y<h en la que el índice de refracción cambia con la altura y. El punto de partida es, (x₀,y₀=h) y su pendiente (dy/dx)_x0=-tanθ

Cuando el índice de refracción depende de la altura y, n(y), la ecuación del camino seguido por la luz es

${\displaystyle \begin{array}{l}{\left(\frac{dy}{dx}\right)}^2=\frac{n^2(y)}{n_0^2(y_0)}\left(1+{\left(\frac{dy}{dx}\right)}_{x_0}^2\right)-1\\ {\left(\frac{dy}{dx}\right)}^2=\frac{n_0^2+ky}{n_0^2+kh}\left(1+{\tan }^2\theta \right)-1\\ \frac{dy}{dx}=\sqrt{\beta y+\gamma },\{\begin{array}{l}\beta =\frac{k}{n^2(h)}\frac{1}{{\cos }^2\theta }\\ \gamma =\frac{n_0^2}{n^2(h)}\frac{1}{{\cos }^2\theta }-1\end{array}\end{array}}$

Integramos

${\displaystyle \begin{array}{l}{\displaystyle \underset{x_0}{\overset{x}{\int }}dx}={\displaystyle \underset{h}{\overset{y}{\int }}\frac{dy}{\sqrt{\beta y+\gamma }}}\\ x-x_0=\frac{2}{\beta }\left(\sqrt{\beta y+\gamma }-\sqrt{\beta h+\gamma }\right)\\ \sqrt{\beta y+\gamma }=\frac{\beta }{2}\left(x-x_0\right)+\sqrt{\beta h+\gamma }\\ \beta y+\gamma =\frac{{\beta }^2}{4}{\left(x-x_0\right)}^2+\beta h+\gamma +\beta \left(x-x_0\right)\sqrt{\beta h+\gamma }\\ y=\frac{\beta }{4}{\left(x-x_0\right)}^2+x\sqrt{\beta h+\gamma }+h-x_0\sqrt{\beta h+\gamma }\end{array}}$

Se trata de la ecuación de una parábola. Teniendo en cuenta que

${\displaystyle \sqrt{\beta h+\gamma }=\sqrt{\frac{1}{{\cos }^2\theta }-1}=\pm \tan \theta }$

El signo deberá ser negativo, para que la pendiente en x₀ sea (dy/dx)_x0=-tanθ

La ecuación del camino que sigue la luz para y<h, es la parábola

${\displaystyle y=\frac{k}{4n^2(h)}\frac{1}{{\cos }^2\theta }{\left(x-x_0\right)}^2-\left(x-x_0\right)\tan \theta +h}$

El mínimo de la parábola se encuentra en x_m, tal que

${\displaystyle \begin{array}{l}\frac{dy}{dx}=\frac{k}{2n^2(h)}\frac{1}{{\cos }^2\theta }\left(x-x_0\right)-\tan \theta =0\\ x_m-x_0=\frac{n^2(h)}{k}\sin \left(2\theta \right)\\ y_m=h-\frac{n^2(h)}{k}{\sin }^2\theta \end{array}}$

Para que el camino que sigue el rayo de luz no toque el suelo, y=0, se tiene que cumplir que y_m≥0, lo que limita los posibles valores del ángulo θ

${\displaystyle \begin{array}{l}\frac{n^2(h)}{k}{\sin }^2\theta \le h\\ \sin \theta \le \frac{\sqrt{kh}}{n(h)}\end{array}}$

La intersección x₁ del camino con la recta y=h es

${\displaystyle \begin{array}{l}h=\frac{k}{4n^2(h)}\frac{1}{{\cos }^2\theta }{\left(x-x_0\right)}^2-\left(x-x_0\right)\tan \theta +h\\ x_1=x_0+\frac{2n^2(h)}{k}\sin \left(2\theta \right)\end{array}}$

La pendiente de la parábola en x₁ es

${\displaystyle {\left(\frac{dy}{dx}\right)}_{x_1}=\frac{k}{2n^2(h)}\frac{1}{{\cos }^2\theta }\left(x_1-x_0\right)-\tan \theta =\tan \theta }$

Es la misma pendiente pero de signo contrario. La parábola es simétrica respecto de la recta x=x_m

• y>h. Camino rectilíneo

A partir de x₁, el índice de refracción es constante, el camino de la luz es una recta de ecuación

${\displaystyle y=\left(x-x_1\right)\tan \theta +h}$

Resumiendo el camino de la luz (véase la figura al principio de este apartado)

${\displaystyle \begin{array}{l}y=\{\begin{array}{l}H-x\tan \theta ,x<x_0\\ \frac{k}{4n^2(h)}\frac{1}{{\cos }^2\theta }{\left(x-x_0\right)}^2-\left(x-x_0\right)\tan \theta +h,x_0\le x\le x_1\\ \left(x-x_1\right)\tan \theta +h,x>x_1\end{array}\\ \sin \theta \le \frac{\sqrt{kh}}{n(h)}\end{array}}$

Representamos el camino seguido por la luz para varios ángulos θ≤θ_m

${\displaystyle {\theta }_m=\arcsin \left(\frac{\sqrt{kh}}{n(h)}\right)}$

con los siguientes datos

• Altura de los ojos del observador, H=1.5 m
• El indice de refracción cambia con la altura, hasta h=0.5 m, luego, se mantiene constante
• El parámetro, k=3·10^-5 m^-1
• El parámetro, n₀=1

k=3.0e-5;
n0=1;
h=0.5; 
H=1.5; %altura de los ojos del observador
th_m=asin(sqrt(k*h)/sqrt(n0^2+k*h));
hold on
thh=linspace(0,th_m,4);
for th=thh(2:end)
    x0=(H-h)/tan(th);
    x1=x0+2*(n0^2+k*h)*sin(2*th)/k;
    line([0,x0],[H,h],'color','r')
    f=@(x) k*(x-x0).^2/(4*(n0^2+k*h)*cos(th)^2)-(x-x0)*tan(th)+h;
    fplot(f,[x0,x1],'color','b')
    line([x1,1200],[h,h+(1200-x1)*tan(th)],'color','r')
end
hold off
ylim([0,2.5])
grid on
xlabel('x')
ylabel('y')
title('Espejismo')

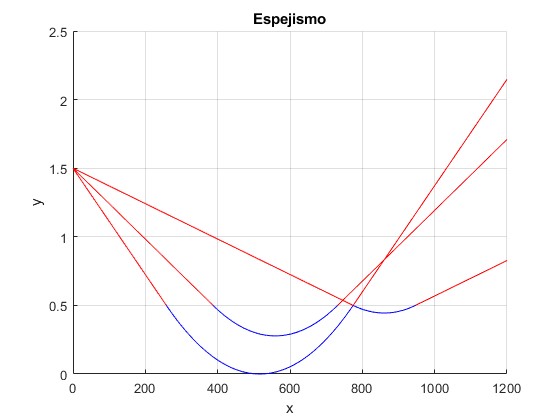
Observamos que para θ=θ_m, la parábola es tangente al eje X, este es el ángulo máximo posible

Para que se vea el extremo de un objeto de altura l, situado en x_c

${\displaystyle \begin{array}{l}l=\left(x_c-x_1\right)\tan \theta +h\\ x_c=x_1+\frac{l-h}{\tan \theta }=x_0+\frac{2n^2(h)}{k}\sin \left(2\theta \right)+\frac{l-h}{\tan \theta }\\ x_c=\frac{H-h}{\tan \theta }+\frac{2n^2(h)}{k}\sin \left(2\theta \right)+\frac{l-h}{\tan \theta }=\frac{2n^2(h)}{k}\sin \left(2\theta \right)+\frac{H+l-2h}{\tan \theta }\end{array}}$

Representamos x_c en función de θ hasta el ángulo límite θ_m, sabiendo que la altura del objeto l=2.2 m

k=3.0e-5;
n0=1;
h=0.5; 
H=1.5; %altura de los ojos del observador
l=2.2; %altura del camello
th_m=asin(sqrt(k*h)/sqrt(n0^2+k*h)); %ángulo límite
f=@(x) 2*(n0^2+k*h)*sin(2*x)/k+(H+l-2*h)./tan(x);
fplot(f,[0.001,th_m])
grid on
ylabel('x_c')
xlabel('\theta')
title('Espejismo')

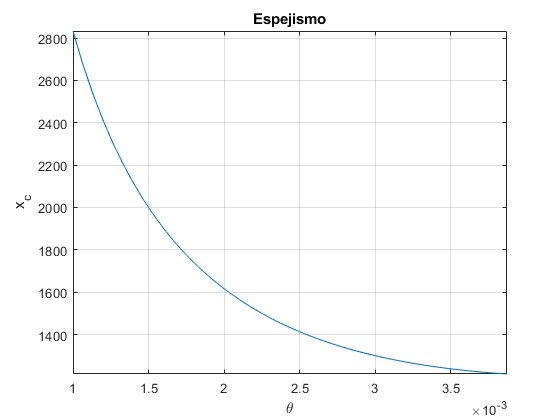
Vemos que x_c es una función decreciente con θ. La posición x_c mínima del objeto para θ_m es

${\displaystyle x_c=\frac{2n^2(h)}{k}\sin \left(2{\theta }_m\right)+\frac{H+l-2h}{\tan {\theta }_m}}$

>> f(th_m)
ans =   1.2135e+03

La distancia mínima al objeto es x_c=1 213 m

En general, dada la posición x_c del objeto, calculamos θ, resolviendo la ecuación transcendente

${\displaystyle x_c=\frac{2n^2(h)}{k}\sin \left(2\theta \right)+\frac{H+l-2h}{\tan \theta }}$

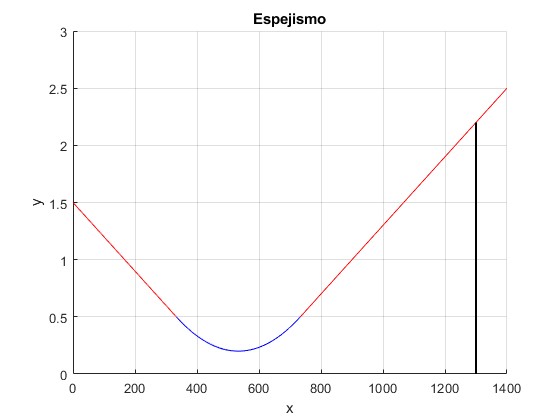
Sea la posición del objeto x_c=1300 m, mayor que la mínima. Representamos el camino que sigue la luz desde el extremo del objeto hasta el observador

k=3.0e-5;
n0=1;
h=0.5; 
H=1.5; %altura de los ojos del observador
l=2.2; %altura del camello
th_m=asin(sqrt(k*h)/sqrt(n0^2+k*h));
xc=1300; %posición del objeto
g=@(x) 2*(n0^2+k*h)*sin(2*x)/k+(H+l-2*h)/tan(x)-xc;
th=fzero(g,[0.001,th_m]); %ángulo
x0=(H-h)/tan(th);
x1=x0+2*(n0^2+k*h)*sin(2*th)/k;
hold on
line([0,x0],[H,h],'color','r')
f=@(x) k*(x-x0).^2/(4*(n0^2+k*h)*cos(th)^2)-(x-x0)*tan(th)+h;
fplot(f,[x0,x1],'color','b')
line([x1,1400],[h,h+(1400-x1)*tan(th)],'color','r')
line([xc,xc],[0,l],'lineWidth',1.5,'color','k')
hold off
grid on
xlabel('x')
ylabel('y')
title('Espejismo')

El índice de refracción disminuye con la altura

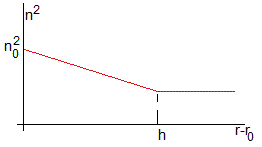
El índice de refracción varía con la distancia radial r de la forma

${\displaystyle n^2(r)=\{\begin{array}{l}{n}_0^2\left(1-k\left(r-R\right)\right),R\le r\le R+h\\ n_0^2\left(1-kh\right),r>R+h\end{array}}$

donde R es el radio de la Tierra y la altura h<<R

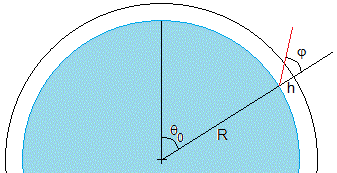
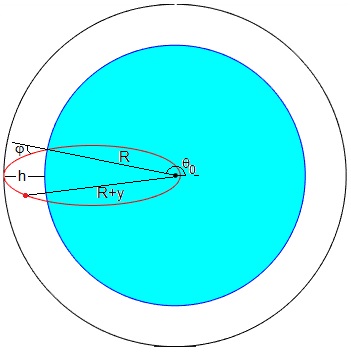
El observador está situado a nivel del mar r=R en la posición θ₀, y recibe un rayo de luz de inclinación φ con la dirección radial.

En la página dedicada al estudio a la propagación de la luz en un medio no homogéneo, en el apartado titulado el 'Ojo de pez de Maxwell', se deduce la ecuación diferencial del camino que sigue la luz en un medio cuyo indice de refracción n(r) varía con la distancia radial

${\displaystyle \frac{d\theta }{dr}=\frac{c}{r\sqrt{r^2{n}^2-c^2}}}$

Donde c es una constante que se determina a partir de las condiciones iniciales, en la posición del observador, (R, θ₀) el rayo de luz hace un ángulo φ con la dirección radial

${\displaystyle \tan \phi \approx \frac{R\Delta \theta }{\Delta r}}$

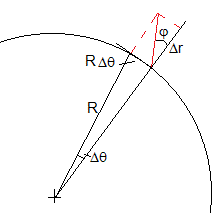
En el límite cuando Δθ→0

${\displaystyle {\left(\frac{d\theta }{dr}\right)}_{{\theta }_{{}_0}}=\frac{1}{R}\tan \phi }$

Por otra parte

${\displaystyle {\left(\frac{d\theta }{dr}\right)}_{{\theta }_{{}_0}}=\frac{c}{R\sqrt{R^2{n}_0^2-c^2}}}$

La constante c vale

${\displaystyle \begin{array}{l}{\tan }^2\phi =\frac{c^2}{R^2{n}_0^2-c^2}\\ c=n_{0}R\sin \phi \end{array}}$

Cuando h<<R podemos hacer la siguiente aproximación, r=R+h

${\displaystyle \frac{1}{R}-\frac{1}{r}\approx \frac{r-R}{R^2}}$

Para r-R<h, expresamos el índice de refracción de la forma aproximada

${\displaystyle n^2(r)=n_0^2\left(1-k{R}^2\left(\frac{1}{R}-\frac{1}{r}\right)\right)}$

La ecuación diferencial del camino que sigue la luz es

${\displaystyle \begin{array}{l}\frac{d\theta }{dr}=\frac{c}{r\sqrt{r^2{n}^2-c^2}}\\ \frac{d\theta }{dr}=\frac{n_{0}R\sin \phi }{r\sqrt{r^2{n}_0^2\left(1-k{R}^2\left(\frac{1}{R}-\frac{1}{r}\right)\right)-R^2{n}_0^2{\sin }^2\phi }}\\ d\theta =\frac{R\sin \phi }{r\sqrt{\left(1-kR\right)r^2+k{R}^{2}r-R^2{\sin }^2\phi }}dr\end{array}}$

Para integrar, dividimos numerador y denominador por r

${\displaystyle d\theta =\frac{\frac{R}{r^2}\sin \phi ·dr}{\sqrt{1-kR+k{R}^2\frac{1}{r}-R^2{\sin }^2\phi \frac{1}{r^2}}}}$

Hacemos el cambio u=1/r, du=-1/r²·dr

${\displaystyle d\theta =\frac{-\sin \phi ·du}{\sqrt{-{\sin }^2\phi ·u^2+ku+\frac{1-kR}{R^2}}}}$

Esta integral la hemos resuelto en la página del capítulo Dinámica celeste, titulado, Ecuación de la trayectoria

${\displaystyle \begin{array}{l}\begin{array}{l}{\displaystyle \int \frac{-du}{\sqrt{-a{u}^2+bu+c}}={\displaystyle \int \frac{-du}{\sqrt{a\left\{\frac{c}{a}+\frac{b^2}{4a^2}-{\left(u-\frac{b}{2a}\right)}^2\right\}}}=}}\hfill \\ a={\sin }^2\phi ,b=k,c=\frac{1-kR}{R^2}\hfill \end{array}\\ {\displaystyle \int \frac{-\sin \phi ·du}{\sqrt{-{\sin }^2\phi ·u^2+ku+\frac{1-kR}{R^2}}}}={\displaystyle \int \frac{-du}{\sqrt{\frac{1-kR}{R^2{\sin }^2\phi }+\frac{k^2}{4{\sin }^4\phi }-{\left(u-\frac{k}{2{\sin }^2\phi }\right)}^2}}}\end{array}}$

Hacemos un nuevo cambio de variable

${\displaystyle \begin{array}{l}u-\frac{k}{2{\sin }^2\phi }=\frac{1}{\sin \phi }\sqrt{\frac{1-kR}{R^2}+\frac{k^2}{4{\sin }^2\phi }}\cos \xi \\ du=-\frac{1}{\sin \phi }\sqrt{\frac{1-kR}{R^2}+\frac{k^2}{4{\sin }^2\phi }}\sin \xi ·d\xi \end{array}}$

La integral se reduce a

${\displaystyle \begin{array}{l}\theta ={\displaystyle \int d\xi }\\ \theta =\xi \end{array}}$

Deshacemos los cambios de variable

${\displaystyle \begin{array}{l}\cos \theta =\frac{\frac{1}{r}-\frac{k}{2{\sin }^2\phi }}{\frac{1}{\sin \phi }\sqrt{\frac{1-kR}{R^2}+\frac{k^2}{4{\sin }^2\phi }}}\\ r=\frac{1}{\frac{k}{2{\sin }^2\phi }+\frac{1}{\sin \phi }\sqrt{\frac{1-kR}{R^2}+\frac{k^2}{4{\sin }^2\phi }}\cos \theta }\\ r=\frac{\frac{2{\sin }^2\phi }{k}}{1+\sqrt{1-\frac{4{\sin }^2\phi }{k^2}\frac{kR-1}{R^2}}\cos \theta }\end{array}}$

El camino que sigue la luz es una porción de elipse

${\displaystyle r=\frac{p}{1+\epsilon \cos \theta },\{\begin{array}{l}p=\frac{2{\sin }^2\phi }{k}\\ \epsilon =\sqrt{1-\frac{4{\sin }^2\phi }{k^2}\frac{kR-1}{R^2}}\end{array}}$

Comprobamos que se cumplen las condiciones iniciales, punto de partida es (R, θ₀)

${\displaystyle R=\frac{p}{1+\epsilon \cos {\theta }_0},\cos {\theta }_0=\frac{1}{\epsilon }\left(\frac{p}{R}-1\right)}$

En cuanto a la pendiente en el punto de partida

${\displaystyle \begin{array}{l}{\left(\frac{dr}{d\theta }\right)}_{{\theta }_0}=\frac{p\epsilon \sin {\theta }_0}{{\left(1+\epsilon \cos {\theta }_0\right)}^2}\\ {\left(\frac{dr}{d\theta }\right)}_{{\theta }_0}=\frac{p\epsilon \sin {\theta }_0}{{\left(1+\epsilon \cos {\theta }_0\right)}^2}=\frac{R}{p}\sqrt{{\epsilon }^2{R}^2-p^2-R^2+2pR}\end{array}}$

Sustituimos el parámero p y la excentricidad ε, obteniendo la condición inicial que nos permitió calcular la constante c

${\displaystyle {\left(\frac{dr}{d\theta }\right)}_{{\theta }_0}=\frac{R}{\tan \phi }}$

Para apreciar la elipse, resolvemos un caso hipotético donde h=2000 km, 2·10⁶ m, que no cumple la condición h<<R. Los datos son

• Radio de la Tierra, R=6370 km,6.37·10⁶ m
• Parámetro, n₀=1
• Parámetro, k=6.0·10^-7 m^-1

El camino que sigue la luz es la porción de elipse, uno de cuyos focos está en el centro de la Tierra, que va desde la posición del emisor (R+y, θ) hasta el observador situado en la posición (R, θ₀) que recibe la luz formando un ángulo φ con la dirección radial

Se ha trazado el camino que sigue la luz para que esté dentro de la región r-R≤h donde hay un gradiente en el índice de refración

La posición más alejada del centro de la Tierra, se produce para θ=π y es r_m=R+h

${\displaystyle r_m=\frac{p}{1-\epsilon }}$

Calculamos el ángulo φ y lo denominamos φ_m

${\displaystyle \begin{array}{l}\epsilon =1-\frac{p}{r_m}\\ {\epsilon }^2=1+\frac{p^2}{r_m^2}-2\frac{p}{r_m}\\ 1-\frac{4{\sin }^2\phi }{k^2}\frac{kR-1}{R^2}=1+\frac{1}{r_m^2}\frac{4{\sin }^4\phi }{k^2}-\frac{1}{r_m}\frac{4{\sin }^2\phi }{k}\\ \frac{4{\sin }^2\phi }{k}\left\{\frac{{\sin }^2\phi }{k{r}_m^2}+\frac{kR-1}{k{R}^2}-\frac{1}{r_m}\right\}=0\\ \sin {\phi }_m=r_m\sqrt{k\left(\frac{1}{r_m}-\frac{kR-1}{k{R}^2}\right)}\end{array}}$

Si φ>φ_m, entonces, r_m<R+h

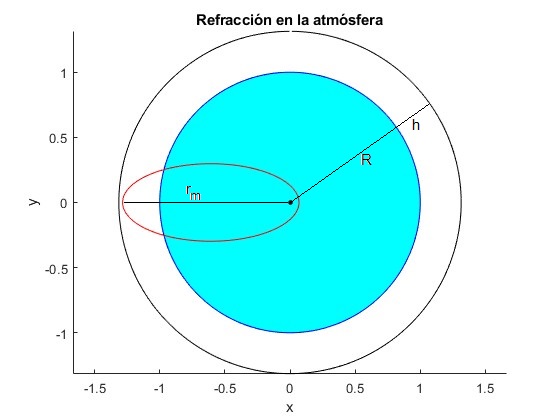
Para representar parte de las dos figuras se ha empleado el código

R=6.37e6; %radio Tierra
n0=1;
k=6.0e-7; 
h=2e6; %altura
rm=R+h;
phi_m=asin(sqrt(rm*(k-rm*(k*R-1)/R^2)));
% phi=phi_m; %ángulo de la tangente
phi=30*pi/180;
p=2*sin(phi)^2/k; 
ex=sqrt(1-4*sin(phi)^2*(k*R-1)/(k*R)^2);

hold on
t=(1:360)*pi/180; %Tierra
xx=cos(t);
yy=sin(t);
fill(xx,yy,'c')
fplot(@(t) cos(t), @(t) sin(t),[0,2*pi],'color','b')
fplot(@(t) (rm/R)*cos(t), @(t) (rm/R)*sin(t),[0,2*pi],'color','k')
plot(0,0,'ko','markersize',3,'markerfacecolor','k')
th=linspace(0,2*pi, 300); %elipse
r=(p/R)./(1+ex*cos(th));
x=r.*cos(th);
y=r.*sin(th);
plot(x,y,'r')
hold off
axis equal
xlabel('x')
ylabel('y')
title('Refracción en la atmósfera')

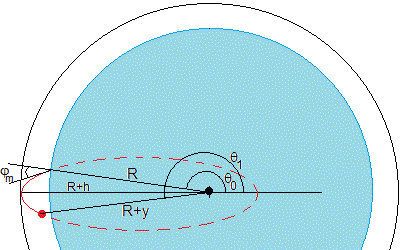
La situación real es aquella en la que el objeto está cerca de la superficie del mar. Los datos son

• Radio de la Tierra, R=6370 km,6.37·10⁶ m
• Parámetro, n₀=1
• Parámetro, k=6.0·10^-7 m^-1
• Altura h=100 m, de la región por encima de la superficie del mar donde hay gradiente en el índice de refracción
• Altura del objeto y=10 m sobre la superficie del mar

R=6.37e6; %radio Tierra
n0=1;
k=6.0e-7; 
h=100; %altura gradiente del índice de refracción
rm=R+h;
phi_m=asin(sqrt(rm*(k-rm*(k*R-1)/R^2)));
phi=phi_m;
p=2*sin(phi)^2/k; 
ex=sqrt(1-4*sin(phi)^2*(k*R-1)/(k*R)^2);
th_0=acos((p/R-1)/ex);

y=10; %altura objeto 10 m
r1=R+y;
%alcanza la altura
th_1=2*pi-acos((p/r1-1)/ex);
disp([th_0, th_1]*180/pi)
dist=R*(th_1-th_0)/1000; %distancia
disp(dist)

  179.6637  180.3191
  72.8697

Fijarse que hay dos ángulos cuyo coseno es el mismo θ y 2π-θ. La distancia al objeto es de 72.87 km

Este ejemplo, nos relaciona la dinámica celeste con la óptica geométrica. Quizás para la situación real (h≈100 m) sea más adecuado aproximar la superficie curva de la Tierra a una superficie plana, como en el primer apartado.

Referencias

WoPhO Problems and Solutions. 2011, Indonesia. Mirage

J. Blanco-García, B. V. Dorrío, F. A. Ribas-Pérez. Photographing mirages above the sea surface. 8 th International Conference on Hands-on Science. Focus on multimedia