Ecuaciones del movimiento

Las fuerzas que actúan sobre la partícula cuando se encuentra en la posición x, moviéndose hacia la derecha son:

• El peso, mg

• La reacción de la superficie, N

• La fuerza de rozamiento, F_r=μN, siendo μ el coeficiente de rozamiento

Cuando la partícula en el instante t, se encuentra en la posición x, el vector velocidad v (cuya dirección es tangente a la trayectoria) forma un ángulo θ con el eje X.

${\displaystyle y=\frac{a}{2}{x}^2\frac{dy}{dx}=\tan \theta =ax}$

Movimiento hacia la derecha

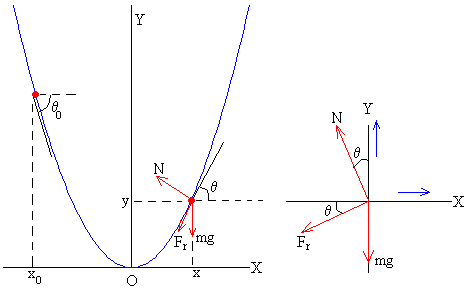
La partícula inicialmente en reposo, parte de la posición x₀ y se moverá hacia la derecha si la componente tangencial del peso es mayor que la fuerza de rozamiento

mgsin|θ₀|≥μ_smgcosθ₀     tan|θ₀|≥μ_s 

Siendo μ_s=μ el coeficiente de rozamiento estático

Descomponemos las fuerzas y escribimos las ecuaciones del movimiento a lo largo del eje X y del eje Y

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-N\sin \theta -F_r\cos \theta \\ m\frac{d^{2}y}{d{t}^2}=N\cos \theta -mg-F_r\sin \theta \end{array}}$

Relacionamos x e y y sus derivadas respecto del tiempo t

${\displaystyle y=\frac{a}{2}{x}^2\frac{dy}{dt}=ax\frac{dx}{dt}\frac{d^{2}y}{d{t}^2}=ax\frac{d^{2}x}{d{t}^2}+a{\left(\frac{dx}{dt}\right)}^2}$

Eliminando N de las dos ecuaciones del movimiento, nos queda la ecuación diferencial

${\displaystyle \left(\frac{1+a^2{x}^2}{ax+\mu }\right)\frac{d^{2}x}{d{t}^2}+a{\left(\frac{dx}{dt}\right)}^2=-g}$

Resolvemos la ecuación diferencial por procedimientos numéricos, con la condición inicial de que la partícula está en reposo v_x=dx/dt=0 en el instante t=0, cuando se encuentra en la posición x₀.

Posición de parada

La partícula se mueve hacia la derecha, hasta que se para momentáneamente en la posición x₁. Para calcular esta posición trasformamos la ecuación diferencial de segundo orden en una de primer orden.

${\displaystyle \begin{array}{l}{v}_x=\frac{dx}{dt}\frac{d^{2}x}{d{t}^2}=v_x\frac{d{v}_x}{dx}\\ \left(\frac{1+a^2{x}^2}{ax+\mu }\right)v_x\frac{d{v}_x}{dx}+a{v}_x=-g\\ -\frac{v_{x}d{v}_x}{g+a{v}_x^2}=\left(\frac{ax+\mu }{1+a^2{x}^2}\right)dx=\frac{1}{a}(\mu +\tan \theta )d\theta \end{array}}$

Integramos la ecuación diferencial entre x₀ ó θ₀ donde la velocidad es 0 y x ó θ donde la velocidad de la partícula es v_x.

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{v_x}{\int }}\frac{-v_{x}d{v}_x}{g+a{v}_x^2}}={\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}(\mu +\tan \theta )d\theta }\\ \ln \left(1+\frac{a{v}_x^2}{g}\right)=2\ln \left(\frac{\cos \theta }{\cos {\theta }_0}\right)-2\mu (\theta -{\theta }_0)\end{array}}$

En la posición θ=θ₁ la velocidad es cero, esta posición se calcula poniendo v_x=0 en la ecuación anterior y resolviendo la ecuación trascendente

${\displaystyle \ln \cos \theta -\mu \theta =\ln \cos {\theta }_0-\mu {\theta }_0}$

Una vez calculado la raíz θ₁,obtenemos la posición x₁ a partir de tanθ₁= a·x₁

Movimiento hacia la izquierda

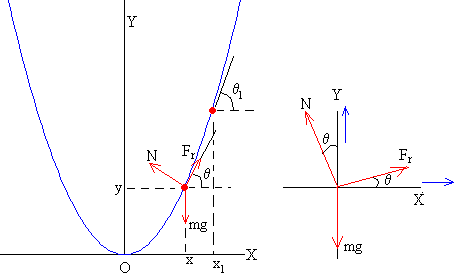
Cuando la partícula llega a la posición x₁, se para momentáneamente e inicia el camino de vuelta si la fuerza de rozamiento es menor que la componente tangencial del peso

mgsinθ₁≥μmgcosθ₁     tan θ₁≥μ 

La fuerza de rozamiento cambia de sentido y las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-N\sin \theta +F_r\cos \theta \\ m\frac{d^{2}y}{d{t}^2}=N\cos \theta -mg+F_r\sin \theta \end{array}}$

Eliminando N de las dos ecuaciones del movimiento nos queda la ecuación diferencial

${\displaystyle \left(\frac{1+a^2{x}^2}{ax-\mu }\right)\frac{d^{2}x}{d{t}^2}+a{\left(\frac{dx}{dt}\right)}^2=-g}$

Es la misma ecuación que hemos obtenido anteriormente cambiando μ→-μ

mu=0.1;  %coeficiente de rozamiento
a=1.9; %parámetro
x0=zeros(1,2);
x0(1)=-2.2;  %posición de partida
x0(2)=0;    %parte del reposo
f=@(t,x) [x(2);(-9.8-a*x(2)^2)*(a*x(1)+sign(x(2))*mu)/(1+a^2*x(1)^2)]; 
tspan=[0 10];
opts=odeset('events',@parabola_ode45);
[t,x,te,xe,ie]=ode45(f,tspan,x0,opts);

hold on
plot(t,x(:,1),'b')
plot(te(ie==1),xe(ie==1),'ro','markersize',4,'markerfacecolor','r')
hold off
grid on
xlabel('t')
ylabel('x');
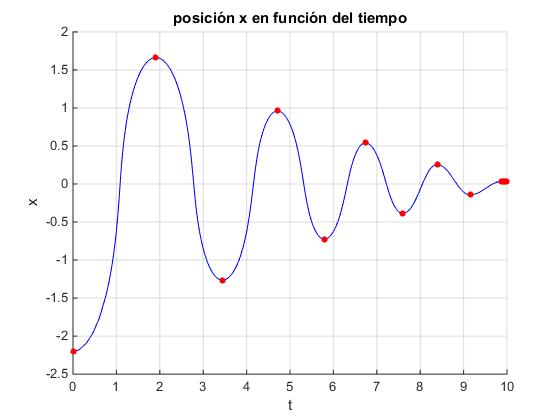
title('posición x en función del tiempo')

Definimos una función para que el procedimiento ode45de MATLAB detecte cuando la velocidad, x(2) en el código, se hace cero, cualquiera que sea la dirección del movimiento.

function [detect,stopin,direction]=parabola_ode45(t,x)
    detect=x(2); 
    stopin=0;
    direction=0; 
end

En la ventana de comandos mostramos estas posiciones, señaladas mediante un punto de color rojo en la ventana gráfica.

>> xe(:,1)
ans =
   -2.2000
    1.6652
   -1.2649
    0.9611
   -0.7250
    0.5405
   -0.3870
    0.2572
   -0.1424
    0.0352

Posición de parada

La partícula sale de la posición x₁ se mueve hacia la izquierda y se para en la posición x₂, que se obtiene resolviendo la ecuación trascendente en la que se ha efectuado el cambio  μ→-μ

${\displaystyle \ln \cos \theta +\mu \theta =\ln \cos {\theta }_1+\mu {\theta }_1}$

Una vez calculada la raíz θ₂, obtenemos la posición x₂, tal que tanθ₂= a·x₂

Y así sucesivamente, hasta que el ángulo tan|θ_n|<μ

Calculamos las sucesivas posiciones x de parada de la partícula, resolviendo la ecuación trascendente

a=1.9;
x0=atan(-2.2*a);  %ángulo de partida
mu=0.1;  %coeficiente de rozamiento

while tan(abs(x0))>abs(mu)
    f=@(x)  log(cos(x))-mu*x;
    g=@(x) f(x)-f(x0);
    x0=fzero(g,[0, -x0]); %ángulo de llegada
    disp(tan(x0)/a)
    mu=-mu;
end

 1.6628
 -1.2611
 0.9567
-0.7217
 0.5357
-0.3836
 0.2545
-0.1397
 0.0326

En el siguiente ejemplo, el programa produce un error

a=0.5;
x0=atan(-4.9*a);  %ángulo de partida
mu=0.2;  %coeficiente de rozamiento

while tan(abs(x0))>abs(mu)
    f=@(x)  log(cos(x))-mu*x;
    g=@(x) f(x)-f(x0);
    x0=fzero(g,[0, -x0]); %ángulo de llegada
    disp(tan(x0)/a)
    mu=-mu;
end

 2.8140
   -1.5114
    0.5784
Error using fzero (line 274)
The function values at the interval endpoints must differ in sign.

La razón, como puede apreciarse en la simulación más abajo, es que la última posición de parada x=0.225 está del mismo lado que la anterior x=0.578. El problema se soluciona con el siguiente código.

a=0.5;
x0=atan(-4.9*a);  %ángulo de partida
mu=0.2;  %coeficiente de rozamiento

while tan(abs(x0))>abs(mu)
    f=@(x)  log(cos(x))-mu*x;
    g=@(x) f(x)-f(x0);
    if sign(g(0))~=sign(g(-x0))
        x0=fzero(g,[0,-x0]); %ángulo de llegada
    else
        x0=fzero(g,0);  %última posición de parada
    end
    disp(tan(x0)/a)
    mu=-mu;
end

    2.8140
   -1.5114
    0.5784
    0.2256

Trabajo de la fuerza de rozamiento

${\displaystyle W=\underset{B}{\overset{A}{{{\displaystyle \int }}^{\text{}}}}\overrightarrow{F_r}·\overrightarrow{dr}=-\underset{B}{\overset{A}{{{\displaystyle \int }}^{\text{}}}}\mu N·ds}$

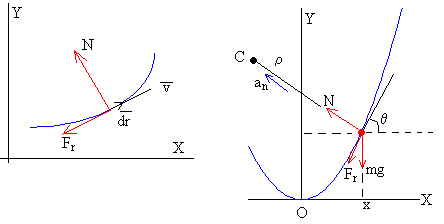
F_r=μN es la fuerza de rozamiento

$\overrightarrow{dr}$ es el vector desplazamiento cuyo módulo es ds.

Calculamos la reacción N de la superficie

La ecuación del movimiento en la dirección normal es

${\displaystyle m\frac{v^2}{\rho }=N-mg\cos \theta }$

donde ρ es el radio de curvatura y el punto C el centro de curvatura

La fórmula del radio de curvatura de una función y=f(x) en un punto de abscisa x, es.

${\displaystyle \rho =\frac{{\left(1+{\left(\frac{dy}{dt}\right)}^2\right)}^{3/2}}{\left|\frac{d^{2}y}{d{t}^2}\right|}}$

Para la parábola de ecuación

${\displaystyle \begin{array}{l}y=\frac{a}{2}{x}^2\frac{dy}{dx}=ax\frac{d^{2}y}{d{x}^2}=a\\ \rho =\frac{{\left(1+{\tan }^2\theta \right)}^{3/2}}{a}=\frac{1}{a{\cos }^3\theta }\end{array}}$

Sabiendo que la componente x de la velocidad de la partícula vale

${\displaystyle \left(1+\frac{a{v}_x^2}{g}\right)={\left(\frac{\cos \theta }{\cos {\theta }_0}\right)}^2\exp \left(-2\mu (\theta -{\theta }_0)\right)}$

La reacción de la superficie N es

${\displaystyle \begin{array}{l}N=mg\cos \theta +ma{v}_x^2\cos \theta =mg\cos \theta \left(1+\frac{a{v}_x^2}{g}\right)=\\ mg\cos \theta {\left(\frac{\cos \theta }{\cos {\theta }_0}\right)}^2\exp \left(-2\mu (\theta -{\theta }_0)\right)\end{array}}$

Calculamos el trabajo W

${\displaystyle \begin{array}{l}W=-{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\mu N·ds}=-\frac{\mu mg}{a{\cos }^2{\theta }_0}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\exp \left(-2\mu (\theta -{\theta }_0)\right)}d\theta =\\ -\frac{mg}{2a{\cos }^2{\theta }_0}\left(1-\exp \left(-2\mu (\theta -{\theta }_0)\right)\right)\end{array}}$

Balance energético

El trabajo W es la diferencia entre la energía final (cuando la partícula se encuentra en la posición x) y la energía inicial (cuando la partícula se encuentra en la posición x₀)

${\displaystyle W=\left(mgy+\frac{1}{2}m{v}^2\right)-mg{y}_0}$

Expresamos las variables y y v en función del ángulo θ de la tangente a la curva.

${\displaystyle y=\frac{a}{2}{x}^2\tan \theta =axv=\frac{v_x}{\cos \theta }}$

Sabiendo que la componente x de la velocidad de la partícula vale

${\displaystyle \left(1+\frac{a{v}_x^2}{g}\right)={\left(\frac{\cos \theta }{\cos {\theta }_0}\right)}^2\exp \left(-2\mu (\theta -{\theta }_0)\right)}$

Después de realizar algunas operaciones llegamos a la misma expresión para el trabajo W.

${\displaystyle W=-\frac{mg}{2a{\cos }^2{\theta }_0}\left(1-\exp \left(-2\mu (\theta -{\theta }_0)\right)\right)}$

Ejemplos

• Sea la parábola y=x², con a=2.0.

• El coeficiente de rozamiento vale μ=0.1

• La partícula sale de la posición x₀=-2.0.

1. Determinar la velocidad de la partícula cuando pasa por el punto más bajo de la trayectoria x=0.0

El ángulo que forma la recta tangente a la curva con el eje X en el punto x₀=-2.0 es

tanθ₀=ax₀, θ₀=-1.32 rad

El ángulo que forma la recta tangente a la curva con el eje X en el punto x=0.0 es θ=0.0 rad.

Calculamos la componente X de la velocidad v_x y a continuación, el módulo de la velocidad v.

$$\begin{gathered} {\displaystyle \left(1+\frac{2.0·v_x^2}{9.8}\right)={\left(\frac{\cos 0}{\cos (-1.32)}\right)}^2\exp \left(-2·0.1·1.32\right) \\ v=\frac{v_x}{\cos \theta }v=7.68\text{m/s}} \end{gathered}$$

2. Posiciones de pausa

La posición de pausa se calcula resolviendo la ecuación trascendente

$$\begin{gathered} {\displaystyle \ln \cos \theta -0.1·\theta =\ln \cos (-1.32)-0.1·(-1.32) \\ {\theta }_1=1.25\text{rad}x=\frac{\tan {\theta }_1}{a}=1.51\text{m}} \end{gathered}$$

como tanθ₁>μ la partícula desliza hacia la izquierda, hasta que se detiene momentáneamente en la posición que se calcula resolviendo la ecuación trascendente en la que se ha sustituido μ→-μ

$$\begin{gathered} {\displaystyle \ln \cos \theta +0.1·\theta =\ln \cos (1.25)+0.1·1.25 \\ {\theta }_2=-1.16\text{rad}x=\frac{\tan {\theta }_2}{a}=-1.15\text{m}} \end{gathered}$$

como tan|θ₂|>μ la partícula desliza hacia la derecha

y así sucesivamente, hasta que tan|θ_n|<0.1

3. Efectuamos el balance energético entre las posiciones inicial x=-2.0 y la posición x=0 .

Energía inicial cuando la partícula se encuentra en x₀=-2.0

${\displaystyle E_0=mg{y}_0=m·9.8·\frac{2.0}{2}{\left(-2.0\right)}^2=39.2·m}$

La energía final cuando la partícula se encuentra en x=0

${\displaystyle E=\frac{1}{2}m{v}^2=\frac{1}{2}m{7.68}^2=29.5m}$

Trabajo de la fuerza de rozamiento

${\displaystyle \begin{array}{l}W=-\frac{mg}{2a{\cos }^2{\theta }_0}\left(1-\exp \left(-2\mu (\theta -{\theta }_0)\right)\right)\\ W=-\frac{m·9.8}{2·2.0·{\cos }^2(-1.32)}\left(1-\exp (-2·0.1·1.32)\right)=-9.70m\end{array}}$

Comprobamos que W=E-E₀

Actividades

Se introduce

• El coeficiente de la fuerza de rozamiento en el control titulado Rozamiento

• El valor del parámetro a que describe la superficie parabólica, en el control titulado Parámetro

• La posición inicial de partida, en el control titulado Posición inicial

Se pulsa el botón titulado Nuevo

Se observa el movimiento de la partícula. Sobre el eje X aparecen señaladas las posiciones de paro momentáneo de la partícula.

También se representa de forma gráfica el balance energético

Referencias

Lapidus I R. Motion of a harmonic oscillator with variable sliding friction. Am. J. Phys. 52 (11) November 1984, pp. 1015-1016