Movimiento sobre una superficie semicircular cóncava
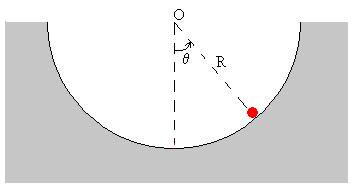
Movimiento sin rozamiento
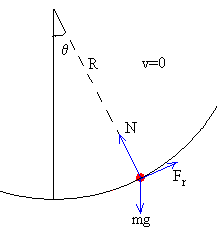
Las fuerzas sobre la partícula:
-
El peso, mg
- La reacción de la superficie circular sobre la que desliza, N
La ecuación del movimiento a lo largo de la dirección radial es
La ecuación del movimiento a lo largo de la dirección tangencial es
que se resuelve por procedimientos numéricos con las condiciones iniciales t=0, θ= -θ0, dθ/dt=0.
Principio de conservación de la energía
A medida que la partícula desliza por la superficie semicircular, va aumentando su velocidad. La energía potencial se va transformando en energía cinética.
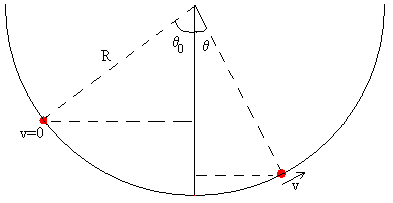
Si la partícula parte de la posición angular –θ0 con velocidad inicial cero. Aplicamos el principio de conservación de la energía para calcular la velocidad v de la partícula cuando se encuentra en la posición θ
Como v=Rdθ/dt, obtenemos la ecuación diferencial de primer orden.
Empleando la fórmula del coseno del ángulo doble cos2A=cos2A-sin2A, y la relación sin2A+cos2A=1.
Haciendo la sustitución
obtenemos
El tiempo que emplea la partícula en desplazarse desde θ=0, (φ=0) hasta θ0 (φ=π/2) es la integral elíptica completa de primera especie.
El tiempo que tarda la partícula desde que sale en la posición –θ0, con velocidad inicial cero, hasta que llega a la posición final θ0 es el doble del tiempo 2·t. El periodo de una oscilación completa de la partícula es P=4·t.
Ejemplo:
Para θ0=60º la integral elíptica vale 1.6858.
>> fi=60*pi/180; >> ellipke(sin(fi/2)^2) ans = 1.6858
El tiempo que tarda la partícula en deslizar sin rozamiento sobre la superficie semicircular de radio R=1 m desde la posición -60º hasta 60º es
Para θ0=15º la integral elíptica vale 1.5776.
>> fi=15*pi/180; >> ellipke(sin(fi/2)^2) ans = 1.5776
El tiempo que tarda la partícula en deslizar sin rozamiento sobre la superficie semicircular de radio R=1 m desde la posición -15º hasta 15º es
Movimiento con rozamiento
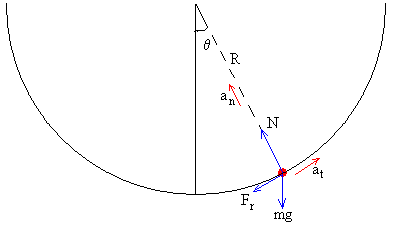
Las fuerzas sobre la partícula:
-
El peso, mg
-
La reacción de la superficie circular sobre la que desliza, N
- La fuerza de rozamiento que se opone al movimiento, Fr=μN
La ecuación del movimiento a lo largo de la dirección radial es
La ecuación del movimiento a lo largo de la dirección tangencial es
mat=-mg·sinθ-Fr
con Fr=μ·N, tenemos la ecuación
(1)
Llamando nos queda la ecuación diferencial
La solución de la ecuación diferencial se compone de dos términos:
La solución particular x1=Asinθ+Bcosθ
Introduciendo la solución particular en la ecuación diferencial, obtenemos los valores de los coeficientes A y B
Buscamos la solución de la ecuación diferencial homogénea
Integrando ambos miembros obtenemos lnx=-2μθ+cte, o bien, x2=C·exp(-2μθ)
La solución completa es x=x1+x2
La constante C se determina a partir de las condiciones iniciales, para θ=θ0, v=0
Comprobamos que cuando θ=θ0, v=0
En la figura, se representa v2/Rg en función del ángulo θ, cuando no hay rozamiento μ=0.0, y para varios valores del coeficiente de rozamiento μ=0.25, μ=0.5 y μ=0.75. La posición de partida es θ0=-60º. La posición de llegada θ se calcula resolviendo la ecuación trascendente con v=0
x0=-60*pi/180; %ángulo de partida
hold on
%sin rozamiento
f=@(x) 2*(cos(x)-cos(x0));
fplot(f,[x0,-x0])
%con rozamiento
for mu=0.25:0.25:0.75
f=@(x) (-exp(-2*mu*(x-x0))*((2-4*mu^2)*cos(x0)-6*mu*sin(x0))
+((2-4*mu^2)*cos(x)-6*mu*sin(x)))/(4*mu^2+1);
xf= fzero(f,0); %ángulo de llegada
fplot(f,[x0,xf])
end
hold off
xlim([-pi/2,pi/2])
set(gca,'XTick',-pi/2:pi/6:pi/2)
set(gca,'XTickLabel',{'-\pi/2','-\pi/3','-\pi/6','0'
,'\pi/6','\pi/3','\pi/2'})
grid on
xlabel('\theta')
ylabel('v^2/(R·g)')
title('Cuadrado de la velocidad en función del ángulo')
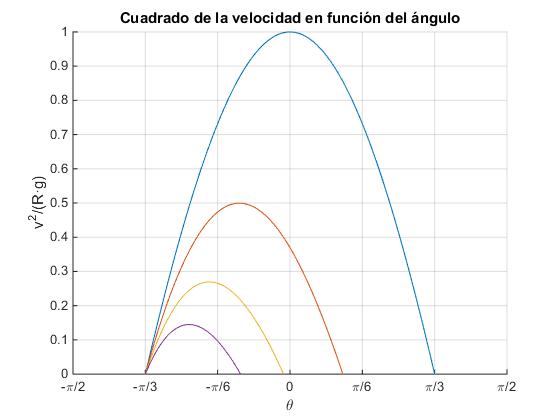
Cuando no hay rozamiento, la posición final cuando la partícula vuelve a pararse es θ=60º. Cuando hay rozamiento la posición final es θ<60º.
Ejemplo:
Sea coeficiente de rozamiento entre la superficie semiesférica y la partícula es μ=0.25. Si la partícula parte de la posición θ0=-60º=-π/3, calcular la velocidad de la partícula cuando pasa por la posición θ=0. El radio de la superficie semicircular es R=1 m.
Si la partícula parte de la posición inicial θ0=-90º=-π/2, la velocidad cuando pasa por la posición más baja θ=0 es
Por ejemplo, para μ=0.25, v2/(Rg)=0.853.
Sucesivas posiciones de parada
Cuando no hay rozamiento, una partícula que parte de la posición -θ0, alcanza su máxima velocidad cuando pasa por el punto más bajo de la trayectoria y se detiene momentáneamente en la posición θ0, inicia el camino de vuelta y se detiene en la posición de partida -θ0, y así, sucesivamente.
Cuando hay rozamiento, la partícula que parte de la posición -θ0, llega hasta la posición θ1, se cumple que θ0>|θ1|. Pueden ocurrir dos casos:
-
Que la componente del peso sea mayor que la fuerza de rozamiento (supondremos que μs= μk= μ)
-
Que tan|θ1|<μ
mgsin|θ1|≥μ·mgcosθ1, o bien que, tan|θ1|≥μ
La partícula inicia su camino de vuelta, llegando a una posición |θ2|<|θ1|
La partícula se para definitivamente
Supongamos que que la partícula prosigue el camino de vuelta hasta la posición θ2. Si se cumple que tan|θ2|≥μ, se inicia por segunda vez su camino de ida. En caso contrario, se detiene permanentemente.
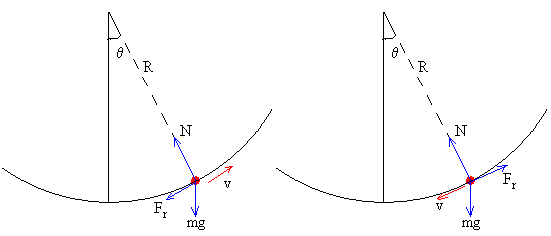
Supongamos que la partícula parte de la posición -θ0. Para calcular la posición de parada θ1 se pone v=0 y se simplifica la ecuación
Calculamos la posición angular θ en la que se detiene la partícula, resolviendo la ecuación trascendente
x0=-60*pi/180; %ángulo de partida mu=0.25; %coeficiente de rozamiento f=@(x) (-3*mu*sin(x)+(1-2*mu^2)*cos(x))*exp(2*mu*x); g=@(x) f(x)-f(x0); fzero(g,0)*180/pi %ángulo de llegada
ans = 21.9153
Si se cumple que tan|θ1|≥μ la partícula continúa moviéndose hacia la izquierda, en caso contrario, se detiene permanentemente.
Supongamos que la partícula realiza el camino de vuelta, la fuerza de rozamiento cambia de signo (véase la figura más arriba), por lo que en la ecuación anterior cambiamos +μ por – μ. La posición de de parada θ2, es la raíz de la ecuación trascendente
Si se cumple que tan|θ2|≥μ la partícula continúa moviéndose hacia la derecha, en caso contrario, se detiene permanentemente.
Supongamos que la partícula vuelve a realizar el camino de ida, la fuerza de rozamiento cambia de signo, por lo que en la ecuación anterior cambiamos +μ por – μ. La posición de parada θ3, es la raíz de la ecuación trascendente
y así, sucesivamente…
Ejemplo: Sea θ=-90º=-π/2, y μ=0.2.
La primera posición θ1 de parada v=0 se calcula resolviendo la ecuación trascendente
La raíz es θ1=44.54º,
Se cumple que tan|θ1|≥0.2, la partícula se mueve hacia la izquierda, la fuerza de rozamiento cambia de signo. Calculamos la posición de parada θ2, resolviendo la ecuación trascendente
La raíz es θ2=-17.38º,
Como tan|θ2|≥0.2 la partícula se mueve hacia la derecha, la fuerza de rozamiento cambia de signo. Calculamos la posición de parada θ3, resolviendo la ecuación trascendente
La raíz es θ3=-5.40º,
Como tan|θ3|<0.2, la partícula se para definitivamente.
x0=-90*pi/180; %ángulo de partida
mu=0.2; %coeficiente de rozamiento
while tan(abs(x0))>abs(mu)
f=@(x) (-3*mu*sin(x)+(1-2*mu^2)*cos(x))*exp(2*mu*x);
g=@(x) f(x)-f(x0);
x0=fzero(g,0); %ángulo de llegada
disp(x0*180/pi)
mu=-mu;
end
44.5603 -17.3993 -5.3886
Balance energético
El trabajo de la fuerza de rozamiento es igual a la energía final de la partícula menos la energía inicial. En la figura del primer apartado, tenemos que
Sustituyendo la larga expresión (2) de v2 en esta ecuación se calcula el trabajo de la fuerza de rozamiento cuando la partícula se encuentra en la posición θ.
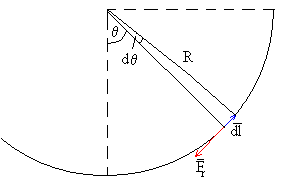
El trabajo de la fuerza de rozamiento se puede calcular también del siguiente modo
dWr=Fr·dl=-Fr·dl·cos180º=-Fr·dl=-μN·R·dθ
Despejamos v2 en la ecuación de la energía, y llegamos a la ecuación diferencial.
e integramos esta ecuación diferencial de modo similar a la de la velocidad.
Para el caso particular de que la partícula parte de la posición más alta θ=-π/2. La ecuación diferencial se hace más simple
Ensayamos una solución particular de la forma
W1=Asenθ+Bcosθ. Obtenemos los valores de los coeficientes A y B
Buscamos la solución de la ecuación diferencial homogénea
La solución completa es Wr=W1+W2
La constante C se determina sabiendo que el trabajo de la fuerza de rozamiento Wr cuando la partícula se encuentra en la posición inicial θ=-π/2 es cero
Ejemplo:
Si μ=0.25, y la partícula parte de la posición θ0=-π/2. La velocidad de la partícula cuando llega a la posición más baja θ=0, es v2/(Rg)=0.853 tal como hemos calculado anteriormente
Calculamos el trabajo de la fuerza de rozamiento Wr de forma indirecta
Calculamos el trabajo de la fuerza de rozamiento Wr de forma directa
Ecuación diferencial del movimiento
-
Movimiento hacia la derecha
-
Movimiento hacia la izquierda
Poniendo , en la ecuación (1), obtenemos la ecuación diferencial del movimiento
que se resuelve por procedimientos numéricos con las condiciones iniciales t=0, θ= -θ0, dθ/dt=0.
La fuerza de rozamiento cambia de signo, por lo que en la ecuación anterior cambiamos +μ por – μ.
mu=0.1; %coeficiente de rozamiento
R=1; %radio
x0=zeros(1,2);
x0(1)=-pi/3; %ángulo de partida
x0(2)=0; %parte del reposo
f=@(t,x) [x(2);-(9.8/R)*(sin(x(1))+sign(x(2))*mu*cos(x(1)))
-sign(x(2))*mu*x(2)^2];
tspan=[0 2.2];
[t,x]=ode45(f,tspan,x0);
plot(t,x(:,1))
set(gca,'YTick',-pi/2:pi/6:pi/2)
set(gca,'YTickLabel',{'-\pi/2','-\pi/3','-\pi/6',
'0','\pi/6','\pi/3','\pi/2'})
grid on
xlabel('t')
ylabel('\theta');
title('Posición angular en función del tiempo')
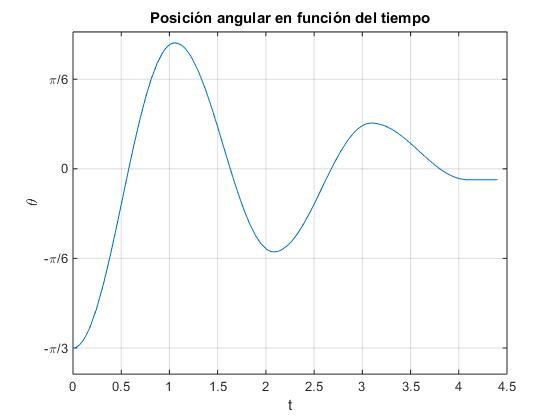
Caso particular:
Cuando no hay rozamiento
Si el ángulo θ es pequeño, aproximamos sinθ≈ θ. Obtenemos la ecuación de un Movimiento Armónico Simple
cuyo periodo es
Ejemplo:
El tiempo que tarda la partícula en deslizar sin rozamiento sobre la superficie semicircular de radio R=1 m, desde la posición - θ0, hasta θ0, cuando este ángulo es pequeño, es P/2
Actividades
Se introduce
-
El coeficiente de rozamiento μ, en el control titulado Rozamiento
-
El ángulo de partida -θ0, en el control titulado Ángulo.
-
El radio de la superficie circular se ha fijado en R=1 m.
Se pulsa el botón titulado Nuevo
Se dibujan las fuerzas sobre la partícula:
-
El peso, mg
-
La fuerza de rozamiento, Fr, cuya dirección es tangente a la trayectoria circular, y cuyo sentido es opuesto a la velocidad
-
La reacción N de la superficie curva, que tiene dirección radial.
En la parte central, se dibujan las energías en forma de diagrama de tarta
-
La energía potencial en color azul
-
La energía cinética en color rojo
-
El trabajo de la fuerza de rozamiento en color negro.
Las posiciones en las que la partícula se detiene momentáneamente v=0, se han marcado en color rojo en la superficie circular cóncava.
Medida del coeficiente cinético
La experiencia clásica de medida del coeficiente cinético, consiste en un bloque que desliza a lo largo de un plano inclinado. Vamos cambiando el ángulo θ que hace el plano inclinado con la horizontal, hasta conseguir que el bloque deslice con movimiento uniforme. El coeficiente de rozamiento vale μ=tanθ
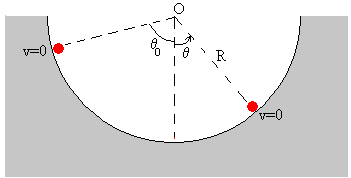
Construimos una la superficie semicircular de radio R. y situamos sobre ella una partícula en la posición inicial θ0. La partícula desliza hasta que se para en la posición final θ, tal como se muestra en la figura.
Para calcular el coeficiente de rozamiento cinético μ, tenemos que resolver por procedimiento numéricos, la ecuación trascendente con v=0.
El código que viene a continuación, calcula el coeficiente cinético μ, cuando se introduce el ángulo inicial de partida θ0 y el ángulo final de llegada θ.
x0=-60*pi/180; %ángulo de partida xf=21.92*pi/180; %ángulo de llegada f=@(mu,x) (-3*mu*sin(x)+(1-2*mu^2)*cos(x))*exp(2*mu*x); g=@(mu) f(mu,x0)-f(mu,xf); roza=fzero(g,0); disp(roza)
0.2500
Referencias
Franklin L. P., Kimmel P. I. Dynamics of circular motion with friction. Am. J. Phys. 48 83) March 1980, pp. 207-210

