Dos osciladores acoplados verticales

Dos partículas unidas a dos muelles en posición vertical con un extremo fijo

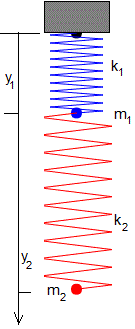
Consideremos dos muelles en posición vertical de constantes k₁ y k₂, unidos a dos partículas de masas m₁ y m₂ tal como se muestra en la figura. La longitud del primer muelle sin deformar es l₁ y la del segundo l₂. En un instante dado t, las posiciones de las partículas son y₁ e y₂ y sus velocidades son dy₁/dt y dy₂/dt

La energía cinética de las dos partículas es

$E_{k} = \frac{1}{2} m_{1} {(\frac{d y_{1}}{d t})}^{2} + \frac{1}{2} m_{2} {(\frac{d y_{2}}{d t})}^{2}$

La energía potencial es la suma de las energías potenciales gravitatorias y elásticas de los dos muelles deformados

$E_{p} = - m_{1} g y_{1} - m_{2} g y_{2} + \frac{1}{2} k_{1} {(y_{1} - l_{1})}^{2} + \frac{1}{2} k_{2} {(y_{2} - y_{1} - l_{2})}^{2}$

La lagrangiana L=E_k-E_p es

$L = \frac{1}{2} m_{1} {(\frac{d y_{1}}{d t})}^{2} + \frac{1}{2} m_{2} {(\frac{d y_{2}}{d t})}^{2} + m_{1} g y_{1} + m_{2} g y_{2} - \frac{1}{2} k_{1} {(y_{1} - l_{1})}^{2} - \frac{1}{2} k_{2} {(y_{2} - y_{1} - l_{2})}^{2}$

Las ecuaciones del movimiento son

$\begin{array}{l} \frac{d}{d t} (\frac{\partial L}{\partial {\dot{y}}_{1}}) - \frac{\partial L}{\partial y_{1}} = 0 \\ m_{1} \frac{d^{2} y_{1}}{d t^{2}} - m_{1} g + k_{1} (y_{1} - l_{1}) - k_{2} (y_{2} - y_{1} - l_{2}) = 0 \\ \frac{d}{d t} (\frac{\partial L}{\partial {\dot{y}}_{2}}) - \frac{\partial L}{\partial y_{2}} = 0 \\ m_{2} \frac{d^{2} y_{2}}{d t^{2}} - m_{2} g + k_{2} (y_{2} - y_{1} - l_{2}) = 0 \end{array}$

o bien

$\begin{array}{l} m_{1} \frac{d^{2} y_{1}}{d t^{2}} + (k_{1} + k_{2}) y_{1} - k_{2} y_{2} = m_{1} g + k_{1} l_{1} - k_{2} l_{2} \\ m_{2} \frac{d^{2} y_{2}}{d t^{2}} - k_{2} y_{1} + k_{2} y_{2} = m_{2} g + k_{2} l_{2} \end{array}$

Posiciones de equilibrio

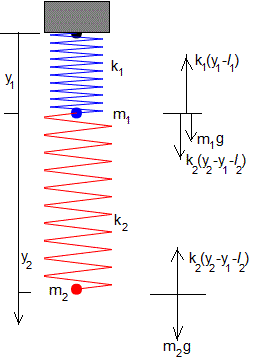
Las posiciones de equilibrio y_e1, y_e2, se calculan poniendo d²y₁/dt²=0, d²y₂/dt²=0 en las ecuaciones del movimiento

${\begin{cases} (k_{1} + k_{2}) y_{e 1} - k_{2} y_{e 2} = m_{1} g + k_{1} l_{1} - k_{2} l_{2} \\ - k_{2} y_{e 1} + k_{2} y_{e 2} = m_{2} g + k_{2} l_{2} \end{cases}$

Alternativamente, calculando las fuerzas que actúan sobre cada una de las dos partículas, tal como se ve en la figura. El muelle de color rojo, ejerce fuerzas iguales y de sentido contrario sobre cada una de las dos partículas, de acuerdo a la tercera ley de Newton

Despejamos en el sistema de dos ecuaciones las incógnitas y_e1, y_e2

$\begin{array}{l} y_{e 1} = \frac{(m_{1} + m_{2}) g}{k_{1}} + l_{1} \\ y_{e 2} = y_{e 1} + \frac{m_{2} g}{k_{2}} + l_{2} \end{array}$

Modos normales de vibración

Llamemos y₁=y_e1+x₁, e y₂=y_e2+x₁. Las ecuaciones del movimiento se simplifican en términos de la variable x

$\begin{array}{l} m_{1} \frac{d^{2} x_{1}}{d t^{2}} + (k_{1} + k_{2}) x_{1} - k_{2} x_{2} = 0 \\ m_{2} \frac{d^{2} x_{2}}{d t^{2}} - k_{2} x_{1} + k_{2} x_{2} = 0 \end{array}$

Buscamos una solución de la forma

x₁=X₁sin(ωt+φ), x₂=X₂sin(ωt+φ)

que representan Movimientos Armónicos Simples de amplitudes X₁, X₂ y frecuencia angular ω.

${\begin{cases} (k_{1} + k_{2} - m_{1} ω^{2}) X_{1} - k_{2} X_{2} = 0 \\ - k_{2} X_{1} + (k_{2} - m_{2} ω^{2}) X_{2} = 0 \end{cases}$

En forma matricial

$(\begin{matrix} \frac{k_{1} + k_{2}}{m_{1}} - ω^{2} & \frac{- k_{2}}{m_{1}} \\ \frac{- k_{2}}{m_{2}} & \frac{k_{2}}{m_{2}} - ω^{2} \end{matrix}) (\begin{matrix} X_{1} \\ X_{2} \end{matrix}) = 0$

Tenemos un sistema homogéneo, los cuadrados de las frecuencias de los modos normales de vibración se calculan haciendo que el determinante de los coeficientes sea igual a cero

$\begin{array}{l} | \begin{matrix} \frac{k_{1} + k_{2}}{m_{1}} - ω^{2} & \frac{- k_{2}}{m_{1}} \\ \frac{- k_{2}}{m_{2}} & \frac{k_{2}}{m_{2}} - ω^{2} \end{matrix} | = 0 \\ ω^{4} - (\frac{k_{2}}{m_{2}} + \frac{k_{1} + k_{2}}{m_{1}}) ω^{2} + \frac{k_{1} k_{2}}{m_{1} m_{2}} = 0 \end{array}$

Obtenemos una ecuación de segundo grado en ω² con dos raíces. Para cada una de las dos frecuencias angulares ω₁ y ω₂ el sistema homogéneo nos proporciona una relación entre X₁ y X₂ que denominaremos r₁ y r₂. Tomando la primera ecuación del sistema homogéneo

$\begin{array}{l} r_{1} = \frac{X_{2}^{(1)}}{X_{1}^{(1)}} = \frac{k_{1} + k_{2} - m_{1} ω_{1}^{2}}{k_{2}} \\ r_{2} = \frac{X_{2}^{(2)}}{X_{1}^{(2)}} = \frac{k_{1} + k_{2} - m_{1} ω_{2}^{2}}{k_{2}} \end{array}$

Movimiento de cada partícula

El movimiento resultante de cada una de las partículas x₁ y x₂ es la combinación lineal de los dos modos normales de vibración de frecuencias angulares ω₁ y ω₂

${\begin{cases} x_{1} = X_{1}^{(1)} \sin (ω_{1} t + φ_{1}) + X_{1}^{(2)} \sin (ω_{2} t + φ_{2}) \\ x_{2} = X_{2}^{(1)} \sin (ω_{1} t + φ_{1}) + X_{2}^{(2)} \sin (ω_{2} t + φ_{2}) = \\ r_{1} X_{1}^{(1)} \sin (ω_{1} t + φ_{1}) + r_{2} X_{1}^{(2)} \sin (ω_{2} t + φ_{2}) \end{cases}$

A partir de las condiciones iniciales

$t = 0 {\begin{cases} x_{1} = x_{01} \\ x_{2} = x_{02} \end{cases} {\begin{cases} \frac{d x_{1}}{d t} = v_{01} \\ \frac{d x_{2}}{d t} = v_{02} \end{cases}$

determinamos las constantes desconocidas: φ₁,φ₂, $X_{1}^{(1)}, X_{1}^{(2)}$

${\begin{cases} x_{01} = X_{1}^{(1)} \sin φ_{1} + X_{1}^{(2)} \sin φ_{2} \\ x_{02} = r_{1} X_{1}^{(1)} \sin φ_{1} + r_{2} X_{1}^{(2)} \sin φ_{2} \\ v_{01} = ω_{1} X_{1}^{(1)} \cos φ_{1} + ω_{2} X_{1}^{(2)} \cos φ_{2} \\ v_{02} = ω_{1} r_{1} X_{1}^{(1)} \cos φ_{1} + ω_{2} r_{2} X_{1}^{(2)} \cos φ_{2} \end{cases}$

El resultado es

$\begin{array}{l} X_{1}^{(1)} \sin φ_{1} = \frac{r_{2} x_{01} - x_{02}}{r_{2} - r_{1}} X_{1}^{(1)} \cos φ_{1} = \frac{r_{2} v_{01} - v_{02}}{ω_{1} (r_{2} - r_{1})} \\ X_{1}^{(2)} \sin φ_{2} = \frac{r_{1} x_{01} - x_{02}}{r_{1} - r_{2}} X_{1}^{(2)} \cos φ_{2} = \frac{r_{1} v_{01} - v_{02}}{ω_{2} (r_{1} - r_{2})} \end{array}$

Conocidos los desplazamientos de las partículas relativos a sus posiciones de equilibrio x₁ y x₂, calculamos los desplazamientos de las partículas y₁=y_e1+x₁, e y₂=y_e2+x₁.

${\begin{cases} y_{1} = X_{1}^{(1)} \sin (ω_{1} t + φ_{1}) + X_{1}^{(2)} \sin (ω_{2} t + φ_{2}) + y_{e 1} \\ y_{2} = r_{1} X_{1}^{(1)} \sin (ω_{1} t + φ_{1}) + r_{2} X_{1}^{(2)} \sin (ω_{2} t + φ_{2}) + y_{e 2} \end{cases}$

Habitualmente, las partículas se desplazan x₀₁ y x₀₂ de sus posiciones de equilibrio con velocidad inicial cero, v₀₁=0, v₀₂=0

Las fases iniciales valen, φ₁=π/2, φ₂=π/2

Las amplitudes valen

$X_{1}^{(1)} = \frac{r_{2} x_{01} - x_{02}}{r_{2} - r_{1}} X_{1}^{(2)} = \frac{r_{1} x_{01} - x_{02}}{r_{1} - r_{2}}$

El movimiento de las partículas para estas condiciones iniciales, se describe mediante las ecuaciones

${\begin{cases} y_{1} = \frac{r_{2} x_{01} - x_{02}}{r_{2} - r_{1}} \cos (ω_{1} t) - \frac{r_{1} x_{01} - x_{02}}{r_{2} - r_{1}} \cos (ω_{2} t) + y_{e 1} \\ y_{2} = r_{1} \frac{r_{2} x_{01} - x_{02}}{r_{2} - r_{1}} \cos (ω_{1} t) - r_{2} \frac{r_{1} x_{01} - x_{02}}{r_{2} - r_{1}} \cos (ω_{2} t) + y_{e 2} \end{cases}$

El primer modo de vibración con frecuencia angular ω₁ se obtiene cuando r₁x₀₁=x₀₂
El segundo modo de vibración con frecuencia angular ω₂ se obtiene cuando r₂x₀₁=x₀₂

Ejemplo

Estudiamos el caso particular, k₁=k₂=k, m₁=2m, m₂=m.

Las frecuencias angulares de los modos de vibración son

$\begin{array}{l} ω^{4} - (\frac{k_{2}}{m_{2}} + \frac{k_{1} + k_{2}}{m_{1}}) ω^{2} + \frac{k_{1} k_{2}}{m_{1} m_{2}} = 0 \\ ω^{4} - \frac{2 k}{m} ω^{2} + \frac{k^{2}}{2 m^{2}} = 0 \\ ω_{1} = \sqrt{\frac{k}{m} (1 + \frac{\sqrt{2}}{2})} ω_{2} = \sqrt{\frac{k}{m} (1 - \frac{\sqrt{2}}{2})} \end{array}$

Calculamos la relación entre amplitudes

$\begin{array}{l} r_{1} = \frac{X_{2}^{(1)}}{X_{1}^{(1)}} = \frac{k_{1} + k_{2} - m_{1} ω_{1}^{2}}{k_{2}} = - \sqrt{2} \\ r_{2} = \frac{X_{2}^{(2)}}{X_{1}^{(2)}} = \frac{k_{1} + k_{2} - m_{1} ω_{2}^{2}}{k_{2}} = \sqrt{2} \end{array}$

Supongamos que los dos partículas se desplazan d de sus posiciones de equilibrio y se sueltan: x₀₁=x₀₂=d, dx₁/dt=0, dx₂/dt=0. Los desplazamientos y de las partículas

${\begin{cases} y_{1} = \frac{d}{2} {(1 - \frac{1}{\sqrt{2}}) \cos (ω_{1} t) + (1 + \frac{1}{\sqrt{2}}) \cos (ω_{2} t)} + \frac{3 m}{k} g + l_{1} \\ y_{2} = \frac{d}{2} {(- \sqrt{2} + 1) \cos (ω_{1} t) + (\sqrt{2} + 1) \cos (ω_{2} t)} + \frac{4 m}{k} g + l_{1} + l_{2} \end{cases}$

Elaboramos un script para representar el movimiento de las partículas en los dos modos de vibración de frecuencias angulares ω₁ y ω₂

k1=20; k2=20; %constantes de los muelles
m1=2; m2=1; %masas de las partículas
l1=1; l2=1; %longitud de los muelles sin deformar

%posiciones de equilibrio
ye1=(m1+m2)*9.8/k1+l1;
ye2=ye1+m2*9.8/k2+l2;

%frecuencias de los modos de vibración
b=k2/m2+(k1+k2)/m1;
c=k1*k2/(m1*m2);
w1=sqrt((b+sqrt(b^2-4*c))/2);
w2=sqrt((b-sqrt(b^2-4*c))/2);

%relación entre amplitudes
r1=(k1+k2-m1*w1^2)/k2;
r2=(k1+k2-m1*w2^2)/k2;

%condiciones iniciales
x01=-0.1;
x02=r1*x01; %primer modo de oscilación
A=(r2*x01-x02)/(r2-r1);
B=(r1*x01-x02)/(r2-r1);

%movimiento de las partículas
y1=@(t) A*cos(w1*t)-B*cos(w2*t)+ye1;
y2=@(t) r1*A*cos(w1*t)-r2*B*cos(w2*t)+ye2;

hold on
fplot(y1,[0,10])
fplot(y2,[0,10])
text(5,3.2, num2str(w1))
line([0,10],[ye1, ye1],'lineStyle','--', 'color','k')
line([0,10],[ye2, ye2],'lineStyle','--', 'color','k')
hold off
grid on
xlabel('t')
ylabel('y_1, y_2')
legend('y_1', 'y_2')
title('Osciladores acoplados')

figure
x02=r2*x01; %segundo modo de oscilación
A=(r2*x01-x02)/(r2-r1);
B=(r1*x01-x02)/(r2-r1);

y1=@(t) A*cos(w1*t)-B*cos(w2*t)+ye1;
y2=@(t) r1*A*cos(w1*t)-r2*B*cos(w2*t)+ye2;

hold on
fplot(y1,[0,10])
fplot(y2,[0,10])
text(5,3.2, num2str(w2))
line([0,10],[ye1,ye1],'lineStyle','--', 'color','k')
line([0,10],[ye2,ye2],'lineStyle','--', 'color','k')
hold off
grid on
xlabel('t')
ylabel('y_1, y_2')
legend('y_1', 'y_2')
title('Osciladores acoplados')

Primer modo de vibración, frecuencia angular ω₂=2.4203

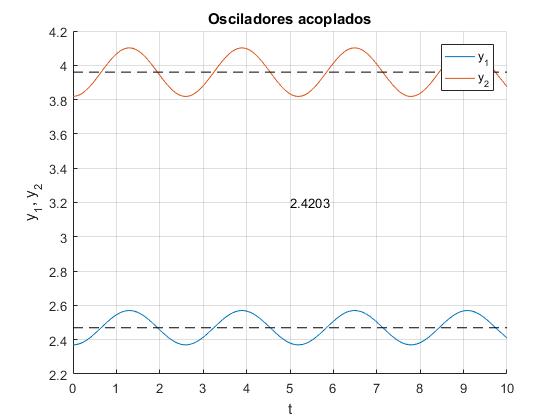
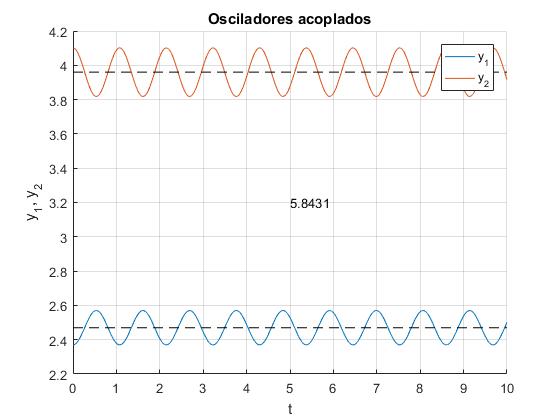
Segundo modo de vibración, frecuencia angular ω₁=5.8431

Actividades

Se introduce

La constante k₁ del primer muelle, en el control titulado k₁
La constante k₂ del segundo muelle, en el control titulado k₂
La masa m₁ de la primera partícula, en el control titulado m₁
La masa m₂ de la segunda partícula, en el control titulado m₂
El desplazamiento x₀₁ de la primera partícula de su posición de equilibrio, en el control titulado x₀₁
El desplazamiento x₀₂ de la segunda partícula de su posición de equilibrio, en el control titulado x₀₂
Las longitudes de los muelles si deformar se han fijado en l₁=1, y l₂=1

Se pulsa el botón titulado Nuevo

Observamos el movimiento de las dos partículas. Representamos la posición de cada una de las dos las partículas en función del tiempo. Una línea a trazos señala la posición de equilibrio de cada partícula

En la parte superior, se proporcionan los datos:

del tiempo t
las posiciones de las partículas y₁ e y₂
las frecuencias angulares de los dos modos de vibración ω₁ y ω₂
Los coeficientes r₁ e r₂

Estos dos datos son importantes para visualizar los modos normales de vibración:

Sea k₁=2, k₂=0.5, m₁=4, m₂=3, y x₀₁=10

Obtenemos r₁=-0.333. Para visualizar el primer modo de vibración de frecuencia angular ω₁=0.816, introducimos en el control titulado x₀₂ el valor r₁x₀₁=-3.333
Obtenemos r₂=4.000. Para visualizar el segundo modo de vibración de frecuencia angular ω₂=0.354, introducimos en el control titulado x₀₂ el valor r₂x₀₁=40

La partícula de color rojo se mantiene por debajo de la partícula de color azul. Podría darse el caso, para unas condiciones iniciales determinadas, que hagan que la partícula de color rojo esté por encima de la de color azul, en ese caso, la simulación se detiene e invita al usuario a probar otros valores de los parámetros

k₁: k₂:
m₁: m₂:
x₀₁: x₀₂:

Dos partículas unidas a tres muelles en posición vertical con los dos extremos fijos

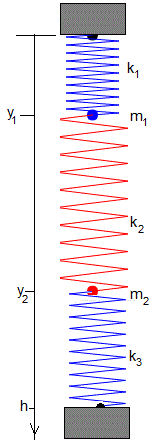
Consideremos tres muelles en posición vertical de constantes k₁, k₂ y k₃, unidos a dos partículas de masas m₁ y m₂ tal como se muestra en la figura. Los extremos del primer muelle y del tercer muelle están fijos y separados una distancia h. La longitud del primer muelle sin deformar es l₁, la del segundo l₂ y la del tercero l₃. En un instante dado t, las posiciones de las partículas son y₁ e y₂ y sus velocidades son dy₁/dt y dy₂/dt

La energía cinética de las dos partículas es

$E_{k} = \frac{1}{2} m_{1} {(\frac{d y_{1}}{d t})}^{2} + \frac{1}{2} m_{2} {(\frac{d y_{2}}{d t})}^{2}$

La energía potencial es la suma de las energías potenciales gravitatorias y elásticas de los tres muelles deformados

$\begin{array}{l} E_{p} = - m_{1} g y_{1} - m_{2} g y_{2} + \\ \frac{1}{2} k_{1} {(y_{1} - l_{1})}^{2} + \frac{1}{2} k_{2} {(y_{2} - y_{1} - l_{2})}^{2} + \frac{1}{2} k_{3} {(h - y_{2} - l_{3})}^{2} \end{array}$

La lagrangiana L=E_k-E_p es

$\begin{array}{l} L = \frac{1}{2} m_{1} {(\frac{d y_{1}}{d t})}^{2} + \frac{1}{2} m_{2} {(\frac{d y_{2}}{d t})}^{2} + m_{1} g y_{1} + m_{2} g y_{2} \\ - \frac{1}{2} k_{1} {(y_{1} - l_{1})}^{2} - \frac{1}{2} k_{2} {(y_{2} - y_{1} - l_{2})}^{2} - \frac{1}{2} k_{3} {(h - y_{2} - l_{3})}^{2} \end{array}$

Las ecuaciones del movimiento son

o bien

Posiciones de equilibrio

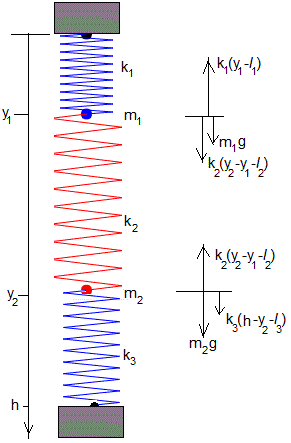
Las posiciones de equilibrio y_e1, y_e2, se calculan poniendo d²y₁/dt²=0, d²y₂/dt²=0 en las ecuaciones del movimiento

${\begin{cases} (k_{1} + k_{2}) y_{e 1} - k_{2} y_{e 2} = m_{1} g + k_{1} l_{1} - k_{2} l_{2} \\ - k_{2} y_{e 1} + (k_{2} + k_{3}) y_{e 2} = m_{2} g + k_{2} l_{2} + k_{3} h - k_{3} l_{3} \end{cases}$

Despejamos en el sistema de dos ecuaciones las incógnitas y_e1, y_e2

$\begin{array}{l} y_{e 1} = \frac{(k_{2} + k_{3}) (m_{1} g + k_{1} l_{1} - k_{2} l_{2}) + k_{2} (m_{2} g + k_{2} l_{2} + k_{3} h - k_{3} l_{3})}{k_{1} k_{2} + k_{1} k_{3} + k_{2} k_{3}} \\ y_{e 2} = \frac{k_{2} y_{e 1} + m_{2} g + k_{2} l_{2} + k_{3} h - k_{3} l_{3}}{k_{2} + k_{3}} \end{array}$

Modos normales de vibración

Llamemos y₁=y_e1+x₁, e y₂=y_e2+x₁. Las ecuaciones del movimiento se simplifican en términos de la variable x

$\begin{array}{l} m_{1} \frac{d^{2} x_{1}}{d t^{2}} + (k_{1} + k_{2}) x_{1} - k_{2} x_{2} = 0 \\ m_{2} \frac{d^{2} x_{2}}{d t^{2}} - k_{2} x_{1} + (k_{2} + k_{3}) x_{2} = 0 \end{array}$

Buscamos una solución de la forma

x₁=X₁sin(ωt+φ), x₂=X₂sin(ωt+φ)

que representan Movimientos Armónicos Simples de amplitudes X₁, X₂ y frecuencia angular ω.

${\begin{cases} (k_{1} + k_{2} - m_{1} ω^{2}) X_{1} - k_{2} X_{2} = 0 \\ - k_{2} X_{1} + (k_{2} + k_{3} - m_{2} ω^{2}) X_{2} = 0 \end{cases}$

En forma matricial

$(\begin{matrix} \frac{k_{1} + k_{2}}{m_{1}} - ω^{2} & \frac{- k_{2}}{m_{1}} \\ \frac{- k_{2}}{m_{2}} & \frac{k_{2} + k_{3}}{m_{2}} - ω^{2} \end{matrix}) (\begin{matrix} X_{1} \\ X_{2} \end{matrix}) = 0$

Tenemos un sistema homogéneo, los cuadrados de las frecuencias de los modos normales de vibración se calculan haciendo que el determinante de los coeficientes sea igual a cero

$\begin{array}{l} | \begin{matrix} \frac{k_{1} + k_{2}}{m_{1}} - ω^{2} & \frac{- k_{2}}{m_{1}} \\ \frac{- k_{2}}{m_{2}} & \frac{k_{2} + k_{3}}{m_{2}} - ω^{2} \end{matrix} | = 0 \\ ω^{4} - (\frac{k_{2} + k_{3}}{m_{2}} + \frac{k_{1} + k_{2}}{m_{1}}) ω^{2} + \frac{k_{1} k_{2} + k_{1} k_{3} + k_{2} k_{3}}{m_{1} m_{2}} = 0 \end{array}$

Movimiento de cada partícula

El movimiento resultante de cada una de las partículas x₁ y x₂ es la combinación lineal de los dos modos normales de vibración de frecuencias angulares ω₁ y ω₂

A partir de las condiciones iniciales

$t = 0 {\begin{cases} x_{1} = x_{01} \\ x_{2} = x_{02} \end{cases} {\begin{cases} \frac{d x_{1}}{d t} = v_{01} \\ \frac{d x_{2}}{d t} = v_{02} \end{cases}$

determinamos las constantes desconocidas: φ₁,φ₂, $X_{1}^{(1)}, X_{1}^{(2)}$

El resultado es

Conocidos los desplazamientos de las partículas relativos a sus posiciones de equilibrio x₁ y x₂, calculamos los desplazamientos de las partículas y₁=y_e1+x₁, e y₂=y_e2+x₁.

Habitualmente, las partículas se desplazan x₀₁ y x₀₂ de sus posiciones de equilibrio con velocidad inicial cero, v₀₁=0, v₀₂=0

Las fases iniciales valen, φ₁=π/2, φ₂=π/2

Las amplitudes valen

$X_{1}^{(1)} = \frac{r_{2} x_{01} - x_{02}}{r_{2} - r_{1}} X_{1}^{(2)} = \frac{r_{1} x_{01} - x_{02}}{r_{1} - r_{2}}$

El movimiento de las partículas para estas condiciones iniciales, se describe mediante las ecuaciones

El primer modo de vibración con frecuencia angular ω₁ se obtiene cuando r₁x₀₁=x₀₂
El segundo modo de vibración con frecuencia angular ω₂ se obtiene cuando r₂x₀₁=x₀₂

Ejemplo

Estudiamos el caso particular, k₁=k₂=k₃=k, m₁=2m, m₂=m.

Las frecuencias angulares de los modos de vibración son

$\begin{array}{l} ω^{4} - (\frac{k_{2} + k_{3}}{m_{2}} + \frac{k_{1} + k_{2}}{m_{1}}) ω^{2} + \frac{k_{1} k_{2} + k_{1} k_{3} + k_{2} k_{3}}{m_{1} m_{2}} = 0 \\ ω^{4} - \frac{3 k}{m} ω^{2} + \frac{3 k^{2}}{2 m^{2}} = 0 \\ ω_{1} = \sqrt{\frac{k}{m} (\frac{3 + \sqrt{3}}{2})} ω_{2} = \sqrt{\frac{k}{m} (\frac{3 - \sqrt{3}}{2})} \end{array}$

Calculamos la relación entre amplitudes

$\begin{array}{l} r_{1} = \frac{X_{2}^{(1)}}{X_{1}^{(1)}} = \frac{k_{1} + k_{2} - m_{1} ω_{1}^{2}}{k_{2}} = - 1 - \sqrt{3} \\ r_{2} = \frac{X_{2}^{(2)}}{X_{1}^{(2)}} = \frac{k_{1} + k_{2} - m_{1} ω_{2}^{2}}{k_{2}} = - 1 + \sqrt{3} \end{array}$

Supongamos que los dos partículas se desplazan d de sus posiciones de equilibrio y se sueltan: x₀₁=x₀₂=d, dx₁/dt=0, dx₂/dt=0. Los desplazamientos y de las partículas

${\begin{cases} y_{1} = \frac{d}{2 \sqrt{3}} {(- 2 + \sqrt{3}) \cos (ω_{1} t) + (2 + \sqrt{3}) \cos (ω_{2} t)} + y_{e 1} \\ y_{2} = \frac{d}{2 \sqrt{3}} {(- 1 + \sqrt{3}) \cos (ω_{1} t) + (1 + \sqrt{3}) \cos (ω_{2} t)} + y_{e 2} \end{cases}$

Elaboramos un script para representar el movimiento de las partículas en los dos modos de vibración de frecuencias angulares ω₁ y ω₂. Se deberá tener cuidado al elegir los valores de los parámetros de modo que y_e2 no sea mayor que h, distancia entre los extremos fijos del primer y íltimo muelle.

k1=20; k2=20; k3=20; %constantes de los muelles
m1=2; m2=1; %masas de las partículas
l1=1; l2=1; l3=1;%longitud de los muelles sin deformar
h=4; %distancia entre los extremos

%posiciones de equilibrio
ye1=((k2+k3)*(m1*9.8+k1*l1-k2*l2)+k2*(m2*9.8+k2*l2+k3*h-k3*l3))/(k1*k2+k1*k3+k2*k3);
ye2=(k2*ye1+m2*9.8+k2*l2+k3*h-k3*l3)/(k2+k3);
if(ye2>=h)
    disp('Modifique los datos')
end
%frecuencias de los modos de vibración
b=(k2+k3)/m2+(k1+k2)/m1;
c=(k1*k2+k1*k3+k2*k3)/(m1*m2);
w1=sqrt((b+sqrt(b^2-4*c))/2);
w2=sqrt((b-sqrt(b^2-4*c))/2);

%relación entre amplitudes
r1=(k1+k2-m1*w1^2)/k2;
r2=(k1+k2-m1*w2^2)/k2;

%condiciones iniciales
x01=-0.1;
x02=r1*x01; %primer modo de oscilación
A=(r2*x01-x02)/(r2-r1);
B=(r1*x01-x02)/(r2-r1);

%movimiento de las partículas
y1=@(t) A*cos(w1*t)-B*cos(w2*t)+ye1;
y2=@(t) r1*A*cos(w1*t)-r2*B*cos(w2*t)+ye2;

hold on
fplot(y1,[0,10])
fplot(y2,[0,10])
text(5,2.5, num2str(w1))
line([0,10],[ye1, ye1],'lineStyle','--', 'color','k')
line([0,10],[ye2, ye2],'lineStyle','--', 'color','k')
hold off
grid on
xlabel('t')
ylabel('y_1, y_2')
legend('y_1', 'y_2')
title('Osciladores acoplados')

figure
x02=r2*x01; %segundo modo de oscilación
A=(r2*x01-x02)/(r2-r1);
B=(r1*x01-x02)/(r2-r1);

y1=@(t) A*cos(w1*t)-B*cos(w2*t)+ye1;
y2=@(t) r1*A*cos(w1*t)-r2*B*cos(w2*t)+ye2;

hold on
fplot(y1,[0,10])
fplot(y2,[0,10])
text(5, 2.5, num2str(w2))
line([0,10],[ye1,ye1],'lineStyle','--', 'color','k')
line([0,10],[ye2,ye2],'lineStyle','--', 'color','k')
hold off
grid on
xlabel('t')
ylabel('y_1, y_2')
legend('y_1', 'y_2')
title('Osciladores acoplados')

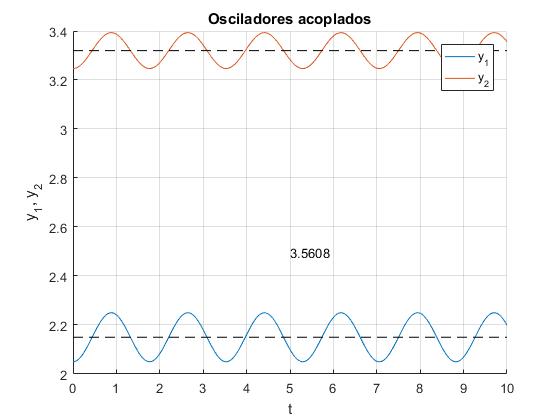
Primer modo de vibración, frecuencia angular ω₁=3.5608

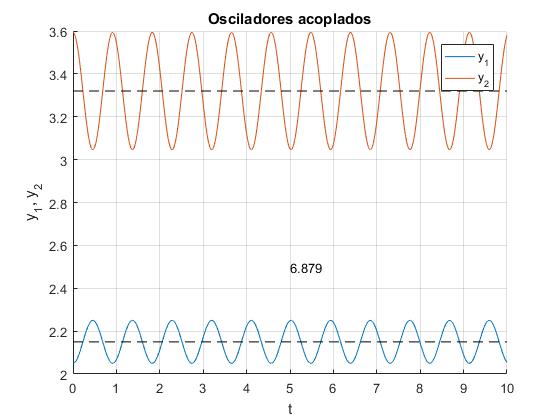
Segundo modo de vibración, frecuencia angular ω₂=6.879

Referencias

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 2052, pp. 579-581

Bernard J. Weigman, Helene F. Perry. Experimental determination of normal frequencies in coupled mechanical oscillator systems using fast Fourier transforms: An advanced undergraduate laboratory. Am. J. Phys. 61 (11) November 1993, pp. 1022-1027