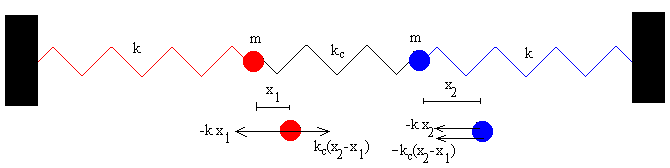
Para estudiar un sistema formado por dos osciladores acoplados, vamos a tomar como modelo el sistema formado por dos partículas iguales de masa m situadas en los extremos de dos muelles de idéntica constante elástica k. El acoplamiento se efectúa uniendo las dos partículas mediante un muelle de constante k_c, tal como se puede ver en la figura.

Oscilaciones libres

Llamemos x₁ y x₂ a los desplazamientos de cada una de las partículas a partir de su posición de equilibrio, medidos como positivos cuando están a la derecha. El muelle de la izquierda se ha estirado x₁, el de la derecha se ha comprimido x₂ y el central se ha deformado x₂-x₁. Las fuerzas sobre cada una de las partículas se indican en la parte inferior de la figura.

• Sobre la partícula de la izquierda, se ejerce una fuerza hacia la izquierda –kx₁, y una fuerza hacia la derecha debido a la deformación del muelle central k_c(x₂-x₁), suponemos que x₂ es mayor que x₁.

• Sobre la partícula derecha, se ejerce una fuerza hacia la izquierda –kx₂ y otra fuerza hacia la izquierda debido a la deformación del muelle central –k_c(x₂-x₁)

El muelle central ejerce fuerzas iguales y de sentido contrario sobre cada una de las partículas.

Aplicamos la segunda ley de Newton a cada una de las partículas, y escribimos las ecuaciones del movimiento en forma de ecuaciones diferenciales de segundo orden

${\displaystyle \begin{array}{l}m\frac{d^2{x}_1}{d{t}^2}=-k{x}_1+k_c(x_2-x_1)\\ m\frac{d^2{x}_2}{d{t}^2}=-k{x}_2-k_c(x_2-x_1)\end{array}}$

Sumando y restando las dos ecuaciones diferenciales tenemos, las ecuaciones diferenciales de un Movimiento Armónico Simple.

${\displaystyle \begin{array}{l}\frac{d^2(x_1+x_2)}{d{t}^2}+\frac{k}{m}(x_1+x_2)=0\\ \frac{d^2(x_1-x_2)}{d{t}^2}+\frac{k+2k_c}{m}(x_1-x_2)=0\end{array}}$

que representan dos movimientos armónicos simples de frecuencias

${\displaystyle {\omega }_a^2=\frac{k}{m}{\omega }_b^2=\frac{k+2k_c}{m}}$

Las soluciones de estas dos ecuaciones, son respectivamente

Ψ_a=x₁+x₂=Ψ_0a sin(ω_at+φ_a)

Ψ_b=x₁-x₂=Ψ_0b sin(ω_bt+φ_b)

Donde las amplitudes Ψ_0a y Ψ_0b y las fases iniciales φ_a y φ_b están determinadas por las condiciones iniciales: posición inicial y velocidad inicial de cada una de las partículas.

Despejando x₁ y x₂ de las dos ecuaciones anteriores tenemos

${\displaystyle \begin{array}{l}{x}_1=\left({\Psi }_{0a}\sin ({\omega }_{a}t+{\phi }_a)+{\Psi }_{0b}\sin ({\omega }_{b}t+{\phi }_b)\right)/2\\ x_2=\left({\Psi }_{0a}\sin ({\omega }_{a}t+{\phi }_a)-{\Psi }_{0b}\sin ({\omega }_{b}t+{\phi }_b)\right)/2\end{array}}$

El movimiento general de dos osciladores acoplados puede considerarse como la superposición de dos modos normales de oscilación de frecuencias angulares ω_a y ω_b.

En el instante t=0, las posiciones iniciales de las partículas son respectivamente x₀₁ y x₀₂. Las velocidades iniciales son cero.

Las ecuaciones se transforman después de algunas operaciones en

${\displaystyle \begin{array}{l}{x}_1=\frac{x_{01}+x_{02}}{2}\cos ({\omega }_{a}t)+\frac{x_{01}-x_{02}}{2}\cos ({\omega }_{b}t)\\ x_2=\frac{x_{01}+x_{02}}{2}\cos ({\omega }_{a}t)-\frac{x_{01}-x_{02}}{2}\cos ({\omega }_{b}t)\end{array}}$

Modos normales de vibración

El primer modo normal de vibración de frecuencia ω_a se obtiene cuando los dos osciladores se mueven en fase x₀₁ es igual a x₀₂. El muelle central no sufre ninguna deformación y por tanto, no ejerce ninguna fuerza sobre las partículas, las cuales se mueven como si no estuvieran acopladas.

${\displaystyle \begin{array}{l}{x}_1=x_{01}\cos ({\omega }_{a}t)\\ x_2=x_{01}\cos ({\omega }_{a}t)\end{array}}$

El segundo modo normal de frecuencia ω_b se obtiene cuando los dos osciladores se mueven en oposición de fase x₀₁ =- x₀₂. Las ecuaciones del movimiento de cada oscilador se reducen a las siguientes.

${\displaystyle \begin{array}{l}{x}_1=x_{01}\cos ({\omega }_{b}t)\\ x_2=-x_{01}\cos ({\omega }_{b}t)\end{array}}$

Experiencia en el aula

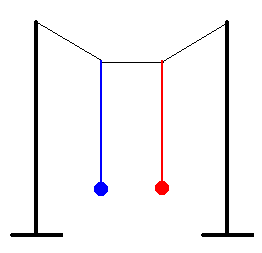
Una experiencia con osciladores acoplados que se realiza en el aula suele sorprender a los estudiantes. Consiste en una cuerda que se sujeta por sus extremos situados a la misma altura. Se atan dos péndulos iguales, a dos puntos simétricos de la cuerda, tal como se indica en la figura. Se desplaza uno de los péndulos, por ejemplo el de color rojo, de su posición de equilibrio y se suelta.

El péndulo empieza a oscilar pero su amplitud disminuye con el tiempo, el otro péndulo de color azul que estaba inicialmente en reposo, empieza a oscilar con una amplitud que aumenta.

Al cabo de un cierto tiempo, el péndulo rojo se para momentáneamente, y el péndulo azul oscila con la máxima amplitud. Luego, se cambian los papeles, el péndulo azul disminuye su amplitud con el tiempo, y el péndulo rojo va aumentando su amplitud.

Se analiza la situación desde el punto de vista energético, cómo la energía fluye de un péndulo al otro a través del acoplamiento. Si el acoplamiento es débil, como es éste el caso, la suma total de las energías de los dos péndulos debe ser constante.

En la experiencia en el aula, se desplaza x₀₁ la primera partícula y la segunda se se deja en la posición de equilibrio x₀₂ es cero. Las ecuaciones del movimiento de las partículas se pueden escribir de forma más simple usando las relaciones trigonométricas cosA+cosB y cosA-cosB.

${\displaystyle \begin{array}{l}{x}_1=x_{01}\cos \frac{{\omega }_a-{\omega }_b}{2}t\cos \frac{{\omega }_a+{\omega }_b}{2}t\\ x_2=x_{01}\sin \frac{{\omega }_a-{\omega }_b}{2}t\sin \frac{{\omega }_a+{\omega }_b}{2}t\end{array}}$

Cuando la amplitud de un oscilador varía con el tiempo, se denomina amplitud modulada. La amplitud del primer oscilador x₀₁cos(ω_a-ω_b)/2 es una función coseno que está adelantada π/2 respecto de la amplitud modulada del segundo oscilador, que es una función seno. Debido a la diferencia de fase entre las dos amplitudes modulantes hay un intercambio de energía entre los dos osciladores. Durante un cuarto de periodo modulante, la amplitud de un oscilador disminuye y la del otro aumenta, dando lugar a una transferencia de energía del primero al segundo. Durante el siguiente cuarto de periodo, la situación se invierte y la energía fluye en dirección opuesta. El proceso se repite continuamente.

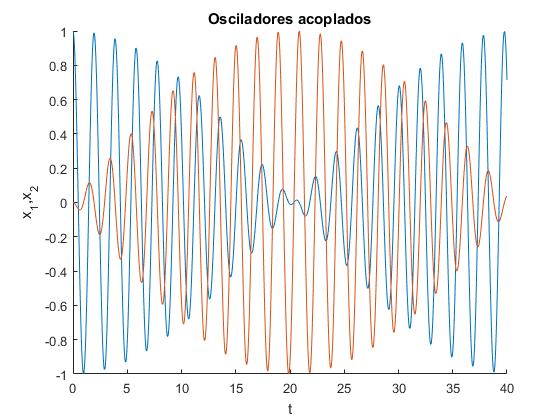
Tomemos un sistema formado por dos muelles de constante k=10, el muelle que une las dos partículas tiene una constante k_c=0.5. La masa de cada una de las partículas es m=1. Las condiciones iniciales se han fijado de modo que se desplaza la primera partícula de la posición de equilibrio y se suelta, x₀₁=1, v₀₁=0, x₀₂=0 y v₀₂=0. Las frecuencias angulares de los dos modos de vibración ω_a y ω_b, son cercanas, ya que la constante del muelle que une las dos partículas k_c es pequeño frente a k.

k=10; kc=0.5; %constantes de los muelles
m=1; %masa
%frecuencias de los modos de vibración
wa=sqrt(k/m);
wb=sqrt((k+2*kc)/m);
x01=1; %se desplaza la primera partícula

x1=@(t) x01*cos((wa-wb)*t/2).*cos((wa+wb)*t/2);
x2=@(t) x01*sin((wa-wb)*t/2).*sin((wa+wb)*t/2);
hold on
fplot(x1,[0,40]);
fplot(x2,[0,40]);
hold off
xlabel('t')
ylabel('x_1,x_2')
title('Osciladores acoplados')

Oscilaciones forzadas

Las fuerzas adicionales que actúan sobre la primera partícula son:

• La fuerza oscilante, F₀cos(ω_ft). Donde F₀ es la amplitud y ω_f la frecuencia angular
• La fuerza de rozamiento proporcional a la velocidad, λ·dx₁/dt

Las fuerza adicional que actúa sobre la segunda partícula es:

• La fuerza de rozamiento proporcional a la velocidad, λ·dx₂/dt

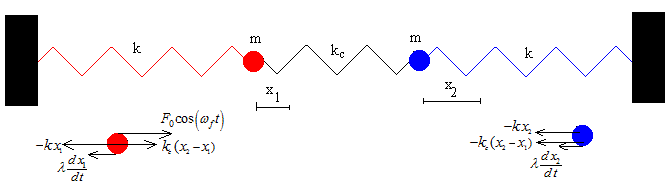
En la parte inferior de figura, se muestran las fuerzas que actúan sobre cada una de las partículas. Las ecuaciones del movimiento son:

${\displaystyle \begin{array}{l}m\frac{d^2{x}_1}{d{t}^2}=-k{x}_1+k_c(x_2-x_1)-\lambda \frac{d{x}_1}{dt}+F_0\cos \left({\omega }_{f}t\right)\hfill \\ m\frac{d^2{x}_2}{d{t}^2}=-k{x}_2-k_c(x_2-x_1)-\lambda \frac{d{x}_2}{dt}\hfill \end{array}}$

Sumanos y restamos miembro a miembro las dos ecuaciones

${\displaystyle \begin{array}{l}\frac{d^2\left(x_1+x_2\right)}{d{t}^2}+\frac{\lambda }{m}\frac{d\left(x_1+x_2\right)}{dt}+\frac{k}{m}\left(x_1+x_2\right)=\frac{F_0}{m}\cos \left({\omega }_{f}t\right)\hfill \\ \frac{d^2\left(x_1-x_2\right)}{d{t}^2}+\frac{\lambda }{m}\frac{d\left(x_1-x_2\right)}{dt}+\frac{k+2k_c}{m}\left(x_1-x_2\right)=\frac{F_0}{m}\cos \left({\omega }_{f}t\right)\hfill \end{array}}$

Llamamos Ψ_a=x₁+x₂, Ψ_b=x₁-x₂, y 2γ=λ/m

${\displaystyle \begin{array}{l}\frac{d^2{\Psi }_a}{d{t}^2}+2\gamma \frac{d{\Psi }_a}{dt}+{\omega }_a^2{\Psi }_a=\frac{F_0}{m}\cos \left({\omega }_{f}t\right)\hfill \\ \frac{d^2{\Psi }_b}{d{t}^2}+2\gamma \frac{d{\Psi }_b}{dt}+{\omega }_b^2{\Psi }_b=\frac{F_0}{m}\cos \left({\omega }_{f}t\right)\hfill \end{array}}$

Estas son las ecuaciones de dos osciladores forzados de frecuencias propias ω_a y ω_b, cuya solución hemos estudiado en dicha página. La solución completa de cada una de las ecuaciones diferenciales, se compone de dos términos, el término transitorio que depende de las condiciones iniciales y el estacionario que es el que permanece después de un tiempo teóricamente infinito

${\displaystyle \begin{array}{l}{\Psi }_a=\left(C_a\cos \left({\omega }_{1}t\right)+D_a\sin \left({\omega }_{1}t\right)\right)\exp \left(-\gamma t\right)+A_a\cos \left({\omega }_{f}t\right)+B_a\sin \left({\omega }_{f}t\right)\\ A_a=\frac{F_0}{m}\frac{{\omega }_a^2-{\omega }_f^2}{{\left({\omega }_a^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}{B}_a=\frac{F_0}{m}\frac{2\gamma {\omega }_f}{{\left({\omega }_a^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}{\omega }_1^2={\omega }_a^2-{\gamma }^2\\ {\Psi }_b=\left(C_b\cos \left({\omega }_{2}t\right)+D_b\sin \left({\omega }_{2}t\right)\right)\exp \left(-\gamma t\right)+A_b\cos \left({\omega }_{f}t\right)+B_b\sin \left({\omega }_{f}t\right)\\ A_b=\frac{F_0}{m}\frac{{\omega }_b^2-{\omega }_f^2}{{\left({\omega }_b^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}{B}_b=\frac{F_0}{m}\frac{2\gamma {\omega }_f}{{\left({\omega }_b^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2}{\omega }_2^2={\omega }_b^2-{\gamma }^2\end{array}}$

El desplazamiento x₁ y x₂ de cada una de las dos partículas es

${\displaystyle \begin{array}{l}{x}_1=\frac{{\Psi }_a+{\Psi }_b}{2}{x}_2=\frac{{\Psi }_a-{\Psi }_b}{2}\\ x_1=\frac{1}{2}\left(\begin{array}{l}{C}_a\cos \left({\omega }_{1}t\right)+D_a\sin \left({\omega }_{1}t\right)\\ +C_b\cos \left({\omega }_{2}t\right)+D_b\sin \left({\omega }_{2}t\right)\end{array}\right)\exp \left(-\gamma t\right)+\frac{A_a+A_b}{2}\cos \left({\omega }_{f}t\right)+\frac{B_a+B_b}{2}\sin \left({\omega }_{f}t\right)\\ x_2=\frac{1}{2}\left(\begin{array}{l}{C}_a\cos \left({\omega }_{1}t\right)+D_a\sin \left({\omega }_{1}t\right)\\ -C_b\cos \left({\omega }_{2}t\right)-D_b\sin \left({\omega }_{2}t\right)\end{array}\right)\exp \left(-\gamma t\right)+\frac{A_a-A_b}{2}\cos \left({\omega }_{f}t\right)+\frac{B_a-B_b}{2}\sin \left({\omega }_{f}t\right)\end{array}}$

Derivando con respecto al tiempo t, obtenemos la velocidad de cada una de las partículas

${\displaystyle \begin{array}{l}\frac{d{x}_1}{dt}=\frac{1}{2}\left(\left(\begin{array}{l}-{\omega }_1{C}_a\sin \left({\omega }_{1}t\right)+{\omega }_1{D}_a\cos \left({\omega }_{1}t\right)\\ -{\omega }_2{C}_b\sin \left({\omega }_{2}t\right)+{\omega }_2{D}_b\cos \left({\omega }_{2}t\right)\end{array}\right)-\gamma \left(\begin{array}{l}{C}_a\cos \left({\omega }_{1}t\right)+D_a\sin \left({\omega }_{1}t\right)\\ +C_b\cos \left({\omega }_{2}t\right)+D_b\sin \left({\omega }_{2}t\right)\end{array}\right)\right)\exp \left(-\gamma t\right)\\ -{\omega }_f\left(\frac{A_a+A_b}{2}\sin \left({\omega }_{f}t\right)-\frac{B_a+B_b}{2}\cos \left({\omega }_{f}t\right)\right)\\ \frac{d{x}_2}{dt}=\frac{1}{2}\left(\left(\begin{array}{l}-{\omega }_1{C}_a\sin \left({\omega }_{1}t\right)+{\omega }_1{D}_a\cos \left({\omega }_{1}t\right)\\ +{\omega }_2{C}_b\sin \left({\omega }_{2}t\right)-{\omega }_2{D}_b\cos \left({\omega }_{2}t\right)\end{array}\right)-\gamma \left(\begin{array}{l}{C}_a\cos \left({\omega }_{1}t\right)+D_a\sin \left({\omega }_{1}t\right)\\ -C_b\cos \left({\omega }_{2}t\right)-D_b\sin \left({\omega }_{2}t\right)\end{array}\right)\right)\exp \left(-\gamma t\right)\\ -{\omega }_f\left(\frac{A_a-A_b}{2}\sin \left({\omega }_{f}t\right)-\frac{B_a-B_b}{2}\cos \left({\omega }_{f}t\right)\right)\end{array}}$

Condiciones iniciales

En el instante t=0,los desplazamientos iniciales de las partículas son x₀₁ y x₀₂, sus velocidades iniciales son v₀₁ y v₀₂, respectivamente

${\displaystyle \begin{array}{l}{x}_{01}=\frac{1}{2}\left(C_a+C_b+A_a+A_b\right)\\ v_{01}=\frac{1}{2}\left({\omega }_1{D}_a+{\omega }_2{D}_b-\gamma C_a-\gamma C_b+{\omega }_f{B}_a+{\omega }_f{B}_b\right)\\ x_{02}=\frac{1}{2}\left(C_a-C_b+A_a-A_b\right)\\ v_{02}=\frac{1}{2}\left({\omega }_1{D}_a-{\omega }_2{D}_b-\gamma C_a+\gamma C_b+{\omega }_f{B}_a-{\omega }_f{B}_b\right)\end{array}}$

Despejamos los coeficientes C_a, C_b, D_a y D_b, que determinan el estado transitorio de cada una de las partículas

${\displaystyle \begin{array}{l}{C}_a=x_{01}+x_{02}-A_a\\ C_b=x_{01}-x_{02}-A_b\\ {\omega }_1{D}_a=v_{01}+v_{02}+\gamma C_a-{\omega }_f{B}_a\\ {\omega }_2{D}_b=v_{01}-v_{02}+\gamma C_b-{\omega }_f{B}_b\end{array}}$

Tomemos un sistema formado por dos muelles iguales cuya constante k=1, el muelle que une las dos partículas tiene una constante grande k_c=10, para que las dos frecuencias angulares de los modos de vibración ω_a y ω_b estén alejadas una de otra. La masa de cada una de las partículas es m=1. El factor de rozamiento γ=0.15, la amplitud de la fuerza oscilante F₀=1. Vamos cambiando la frecuencia de la fuerza oscilante ω_f. Las condiciones iniciales se han fijado de modo que se desplaza la primera partícula de la posción de equilibrio y se suelta, x₀₁=1, v₀₁=0, x₀₂=0 y v₀₂=0

k=1; kc=10; %constantes de los muelles
m=1; %masa
wa=sqrt(k/m); %primer modo  
wb=sqrt((k+2*kc)/m; %segundo modo

g=0.15; %coeficiente de rozamiento
F0=1; %amplitud de la fuerza oscilante F0/m
wf=sqrt(3); %frecuencia angular de la fuerza oscilante 
%condiciones iniciales
x01=1; x02=0; %posiciones iniciales
v01=0; v02=0; %velocidades iniciales

%frecuencias 
w1=sqrt(wa^2-g^2);
w2=sqrt(wb^2-g^2);

%amplitudes del estado estacionario
Aa=F0*(wa^2-wf^2)/((wa^2-wf^2)^2+4*g^2*wf^2);
Ab=F0*(wb^2-wf^2)/((wb^2-wf^2)^2+4*g^2*wf^2);
Ba=F0*(2*g*wf)/((wa^2-wf^2)^2+4*g^2*wf^2);
Bb=F0*(2*g*wf)/((wb^2-wf^2)^2+4*g^2*wf^2);

%coeficientes del estado transitorio
Ca=(x01+x02)-Aa;
Cb=(x01-x02)-Ab;
Da=((v01+v02)+g*Ca-wf*Ba)/w1;
Db=((v01-v02)+g*Cb-wf*Bb)/w2;

x1=@(t) (Ca*cos(w1*t)+Da*sin(w1*t)+Cb*cos(w2*t)+Db*sin(w2*t)).*exp(-g*t)/2+
(Aa+Ab)*cos(wf*t)/2+(Ba+Bb)*sin(wf*t)/2;
x2=@(t) (Ca*cos(w1*t)+Da*sin(w1*t)-Cb*cos(w2*t)-Db*sin(w2*t)).*exp(-g*t)/2+
(Aa-Ab)*cos(wf*t)/2+(Ba-Bb)*sin(wf*t)/2;

%representación gráfica
hold on
fplot(x1,[0,40]);
fplot(x2,[0,40]);
hold off
grid on
legend('x_1','x_2')
title('Dos osciladores acoplados, forzados')
ylabel('x_1,x_2')
xlabel('t')

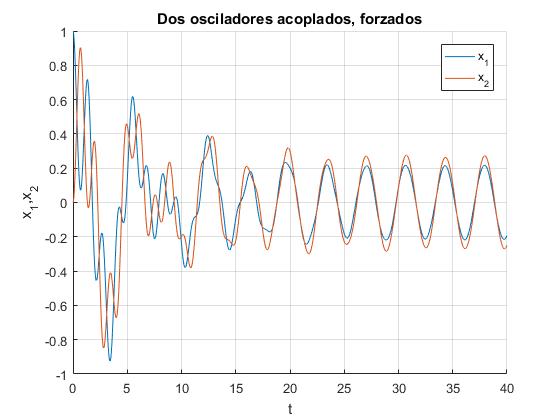
Observamos el estado transitorio y su evolución hacia el estado estacionario, donde las amplitudes de las oscilaciones son constantes

Amplitudes y fases en el estado estacionario

Después de un tiempo teóricamente infinito, el estado transitorio desaparece, se ha establecido el estado estacionario independiente de las condiciones iniciales. La posición de cada una de las partículas viene dada por

${\displaystyle \begin{array}{l}{x}_1=\frac{A_a+A_b}{2}\cos \left({\omega }_{f}t\right)+\frac{B_a+B_b}{2}\sin \left({\omega }_{f}t\right)\\ x_2=\frac{A_a-A_b}{2}\cos \left({\omega }_{f}t\right)+\frac{B_a-B_b}{2}\sin \left({\omega }_{f}t\right)\end{array}}$

Para calcular la amplitud A₁ y la fase φ₁ de la oscilación de la primera partícula y la amplitud A₂ y la fase φ₂ de la oscilación de la segunda partícula, resolvemos los sistema de dos ecuaciones

${\displaystyle \begin{array}{l}{x}_1=A_1\sin \left({\omega }_{f}t+{\phi }_1\right)=\left(A_1\sin {\phi }_1\right)\cos \left({\omega }_{f}t\right)+\left(A_1\cos {\phi }_1\right)\sin \left({\omega }_{f}t\right)\\ \{\begin{array}{l}{A}_1\sin {\phi }_1=\frac{A_a+A_b}{2}\\ A_1\cos {\phi }_1=\frac{B_a+B_b}{2}\end{array}\\ x_2=A_2\sin \left({\omega }_{f}t+{\phi }_2\right)=\left(A_2\sin {\phi }_2\right)\cos \left({\omega }_{f}t\right)+\left(A_2\cos {\phi }_2\right)\sin \left({\omega }_{f}t\right)\\ \{\begin{array}{l}{A}_2\sin {\phi }_2=\frac{A_a-A_b}{2}\\ A_2\cos {\phi }_2=\frac{B_a-B_b}{2}\end{array}\end{array}}$

Despejamos las aplitudes A₁ y A₂

${\displaystyle \begin{array}{l}{A}_1=\frac{1}{2}\frac{F_0}{m}\sqrt{\frac{{\omega }_a^4+{\omega }_b^4+4{\omega }_f^4-4{\omega }_a^2{\omega }_f^2-4{\omega }_b^2{\omega }_f^2+2{\omega }_a^2{\omega }_b^2+16{\gamma }^2{\omega }_f^2}{\left({\left({\omega }_a^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2\right)\left({\left({\omega }_b^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2\right)}}\\ A_2=\frac{1}{2}\frac{F_0}{m}\sqrt{\frac{{\left({\omega }_a^2-{\omega }_b^2\right)}^2}{\left({\left({\omega }_a^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2\right)\left({\left({\omega }_b^2-{\omega }_f^2\right)}^2+4{\gamma }^2{\omega }_f^2\right)}}\end{array}}$

k=1; kc=10; %constantes de los muelles
m=1; %masa
wa=sqrt(k/m); %primer modo  
wb=sqrt((k+2*kc)/m); %segundo modo
g=0.15; %coeficiente de rozamiento
F0=1; %amplitud de la fuerza oscilante F0/m

%amplitudes
wf=linspace(0,7,100); %frecuencia angular de la fuerza oscilante 
den=((wa^2-wf.^2).^2+4*g^2*wf.^2).*((wb^2-wf.^2).^2+4*g^2*wf.^2);
A1=sqrt((wa^4+wb^4+4*wf.^4-4*wa^2*wf.^2-4*wb^2*wf.^2+2*wa^2*wb^2+
16*g^2*wf.^2)./den)*F0/2;
A2=sqrt((wb^2-wa^2)^2./den)*F0/2;

%representación gráfica
hold on
plot(wf,A1);
plot(wf,A2);
line([wa,wa],[0,1.6], 'LineStyle','--');
line([wb,wb],[0,1.6], 'LineStyle','--');
title('Dos osciladores acoplados, forzados')
legend('A_1','A_2')
ylabel('A_1,A_2')
xlabel('w_f')
grid on
hold off

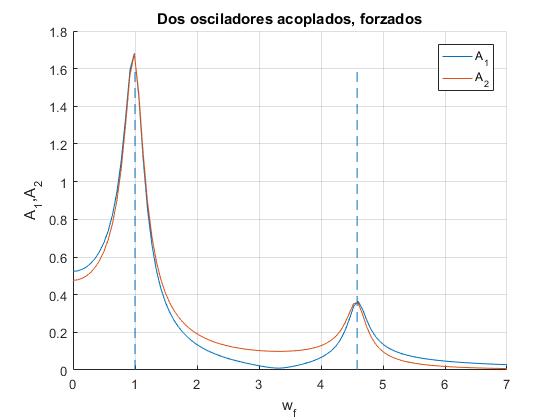
Las amplitudes A₁ y A₂ presentan un máximo para las frecuencias angulares próximas a ω_a y ω_b de los dos modos de vibración, representadas mediante líneas verticales a trazos

Despejamos las fases, φ₁ y φ₂

${\displaystyle \tan {\phi }_1=\frac{A_a+A_b}{B_a+B_b}\tan {\phi }_2=\frac{A_a-A_b}{B_a-B_b}}$

k=1; kc=10; %constantes de los muelles
m=1; %masa
wa=sqrt(k/m); %primer modo  
wb=sqrt((k+2*kc)/m); %segundo modo
g=0.15; %coeficiente de rozamiento
F0=1; %amplitud de la fuerza oscilante F0/m

wf=linspace(0,7,200); %frecuencia angular de la fuerza oscilante 

%coeficientes del estado estacionario
Aa=F0*(wa^2-wf.^2)./((wa^2-wf.^2).^2+4*g^2*wf.^2);
Ab=F0*(wb^2-wf.^2)./((wb^2-wf.^2).^2+4*g^2*wf.^2);
Ba=F0*(2*g*wf)./((wa^2-wf.^2).^2+4*g^2*wf.^2);
Bb=F0*(2*g*wf)./((wb^2-wf.^2).^2+4*g^2*wf.^2);

%fases
fi1=atan2((Aa+Ab),(Ba+Bb));
fi2=atan2((Aa-Ab),(Ba-Bb));

%representación gráfica
hold on
plot(wf,fi1);
plot(wf,fi2);
line([wa,wa],[-pi,pi], 'LineStyle','--');
line([wb,wb],[-pi,pi], 'LineStyle','--');
title('Dos osciladores acoplados, forzados')
ylabel('\phi_1,\phi_2')
xlabel('w_f')
set(gca,'YTick',-pi:pi/4:pi)
set(gca,'YTickLabel',{'-\pi','-3\pi/4','-\pi/2','-\pi/4','0',
'\pi/4','\pi/2','3\pi/4','\pi'})
legend('\phi_1','\phi_2', 'location','northwest')
grid on
hold off

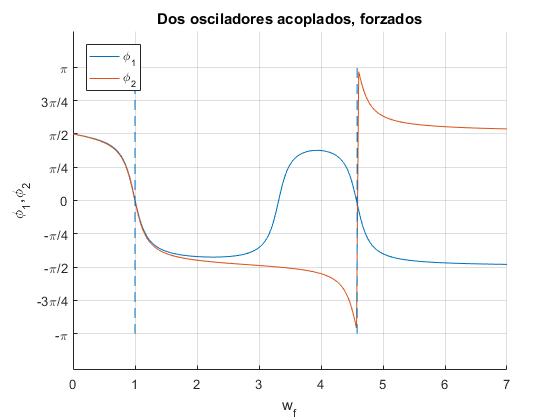
Las fases φ₁ y φ₂ presentan un comportamiento más complejo. Las líneas verticales a trazos, señalan las frecuencias de los dos modos de vibración ω_a y ω_b

Cuando no hay rozamiento γ=0

Poniendo γ=0, los coeficientes valen

${\displaystyle \begin{array}{l}{A}_a=\frac{F_0}{m}\frac{1}{{\omega }_a^2-{\omega }_f^2}{B}_a=0{\omega }_1={\omega }_a\\ A_b=\frac{F_0}{m}\frac{1}{{\omega }_b^2-{\omega }_f^2}{B}_b=0{\omega }_2={\omega }_b\\ C_a=x_{01}+x_{02}-A_a\\ C_b=x_{01}-x_{02}-A_b\\ {\omega }_a{D}_a=v_{01}+v_{02}\\ {\omega }_b{D}_b=v_{01}-v_{02}\end{array}}$

El desplazamiento x₁ y x₂ de las partículas en función del tiempo t es

${\displaystyle \begin{array}{l}{x}_1=\frac{1}{2}\left(\begin{array}{l}{C}_a\cos \left({\omega }_{a}t\right)+D_a\sin \left({\omega }_{a}t\right)\\ +C_b\cos \left({\omega }_{b}t\right)+D_b\sin \left({\omega }_{b}t\right)\end{array}\right)+\frac{A_a+A_b}{2}\cos \left({\omega }_{f}t\right)\\ x_2=\frac{1}{2}\left(\begin{array}{l}{C}_a\cos \left({\omega }_{a}t\right)+D_a\sin \left({\omega }_{a}t\right)\\ -C_b\cos \left({\omega }_{b}t\right)-D_b\sin \left({\omega }_{b}t\right)\end{array}\right)+\frac{A_a-A_b}{2}\cos \left({\omega }_{f}t\right)\end{array}}$

Parecería que cuando la frecuencia de la fuerza oscilante ω_f se hace igual a las frecuencias de los modos de vibración ω_a o ω_b, los coeficientes A_a o A_b tendieran a infinito. Sin embrago, el cociente

${\displaystyle \underset{{\omega }_f\to {\omega }_0}{\lim }\left(\frac{\cos ({\omega }_{f}t)-\cos ({\omega }_{0}t)}{{\omega }_0^2-{\omega }_f^2}\right)=\frac{t\sin ({\omega }_{0}t)}{2{\omega }_0}}$

donde el subíndice '0' representa 'a' o 'b', tal como hemos visto al estudiar el caso de las oscilaciones forzadas con rozamiento nulo γ=0

>> syms w0 wf t;
>> limit((cos(wf*t)-cos(w0*t))/(w0^2-wf^2),wf,w0)
ans =(t*sin(t*w0))/(2*w0)

Supongamos que desplazamos la primera partícula x₀₁ y la soltamos: x₀₂=0, v₀₁=0, v₀₂=0. Los desplazamientos x₁ y x₂ de las partículas en función del tiempo t son

${\displaystyle \begin{array}{l}{x}_1=\frac{1}{2}\left(\left(x_{01}-A_a\right)\cos \left({\omega }_{a}t\right)+\left(x_{01}-A_b\right)\cos \left({\omega }_{b}t\right)\right)+\frac{A_a+A_b}{2}\cos \left({\omega }_{f}t\right)\\ x_2=\frac{1}{2}\left(\left(x_{01}-A_a\right)\cos \left({\omega }_{a}t\right)-\left(x_{01}-A_b\right)\cos \left({\omega }_{b}t\right)\right)+\frac{A_a-A_b}{2}\cos \left({\omega }_{f}t\right)\\ x_1=\frac{1}{2}{x}_{01}\left(\cos \left({\omega }_{a}t\right)+\cos \left({\omega }_{b}t\right)\right)+\frac{F_0}{m}\left(\frac{\cos \left({\omega }_{f}t\right)-\cos \left({\omega }_{a}t\right)}{{\omega }_a^2-{\omega }_f^2}+\frac{\cos \left({\omega }_{f}t\right)-\cos \left({\omega }_{b}t\right)}{{\omega }_b^2-{\omega }_f^2}\right)\\ x_2=\frac{1}{2}{x}_{01}\left(\cos \left({\omega }_{a}t\right)-\cos \left({\omega }_{b}t\right)\right)+\frac{F_0}{m}\left(\frac{\cos \left({\omega }_{f}t\right)-\cos \left({\omega }_{a}t\right)}{{\omega }_a^2-{\omega }_f^2}-\frac{\cos \left({\omega }_{f}t\right)-\cos \left({\omega }_{b}t\right)}{{\omega }_b^2-{\omega }_f^2}\right)\end{array}}$

Oscilaciones amortiguadas

Las oscilaciones amortiguadas se producen cuando no se aplica una fuerza oscilante a la primera partícula, F₀=0, ω_f=0. No hay solución particular que describe el estado estacionario, los coeficientes A_a, A_b, B_a, B_b, son nulos. Los desplazamientos x₁ y x₂ de las partículas en función del tiempo t son

${\displaystyle \begin{array}{l}{x}_1=\frac{1}{2}\left(C_a\cos \left({\omega }_{1}t\right)+D_a\sin \left({\omega }_{1}t\right)+C_b\cos \left({\omega }_{2}t\right)+D_b\sin \left({\omega }_{2}t\right)\right)\exp \left(-\gamma t\right)\\ x_2=\frac{1}{2}\left(C_a\cos \left({\omega }_{1}t\right)+D_a\sin \left({\omega }_{1}t\right)-C_b\cos \left({\omega }_{2}t\right)-D_b\sin \left({\omega }_{2}t\right)\right)\exp \left(-\gamma t\right)\end{array}}$

Donde los coeficientes C_a, C_b, D_a, D_b, vienen determinados por las condiciones iniciales. Supongamos que desplazamos la primera partícula x₀₁ y la soltamos: x₀₂=0, v₀₁=0, v₀₂=0. Los desplazamientos x₁ y x₂ de las partículas en función del tiempo t son

${\displaystyle \begin{array}{l}{x}_1=\frac{1}{2}{x}_{01}\left(\cos \left({\omega }_{1}t\right)+\cos \left({\omega }_{2}t\right)+\gamma \left(\frac{\sin \left({\omega }_{1}t\right)}{{\omega }_1}+\frac{\sin \left({\omega }_{2}t\right)}{{\omega }_2}\right)\right)\exp \left(-\gamma t\right)\\ x_2=\frac{1}{2}{x}_{01}\left(\cos \left({\omega }_{1}t\right)-\cos \left({\omega }_{2}t\right)+\gamma \left(\frac{\sin \left({\omega }_{1}t\right)}{{\omega }_1}-\frac{\sin \left({\omega }_{2}t\right)}{{\omega }_2}\right)\right)\exp \left(-\gamma t\right)\end{array}}$

Tomemos de nuevo el sistema estudiado en las oscilaciones libres, formado por dos muelles de constante k=10, el muelle que une las dos partículas tiene una constante k_c=0.5. La masa de cada una de las partículas es m=1. Las condiciones iniciales se han fijado de modo que se desplaza la primera partícula de la posción de equilibrio y se suelta, x₀₁=1, v₀₁=0, x₀₂=0 y v₀₂=0. Las frecuencias angulares de los dos modos de vibración ω_a y ω_b, son cercanas, ya que la constante del muelle que une las dos partículas k_c es peueño frente a k.

k=10; kc=0.5; %constantes de los muelles
m=1; %masa
wa=sqrt(k/m); %frecuencias angulares de los modos de vibración
wb=sqrt((k+2*kc)/m);
g=0.15; %coeficiente de rozamiento

%frecuencias 
w1=sqrt(wa^2-g^2);
w2=sqrt(wb^2-g^2);
x01=1; %se desplaza la primera partícula

x1=@(t) x01*(cos(w1*t)+cos(w2*t)+g*(sin(w1*t)/w1+sin(w2*t)/w2))*exp(-g*t)/2;
x2=@(t) x01*(cos(w1*t)-cos(w2*t)+g*(sin(w1*t)/w1-sin(w2*t)/w2))*exp(-g*t)/2;
hold on
fplot(x1,[0,30]);
fplot(x2,[0,30]);
hold off
xlabel('t')
ylabel('x_1,x_2')
legend('x_1','x_2')
grid on
title('Osciladores acoplados')

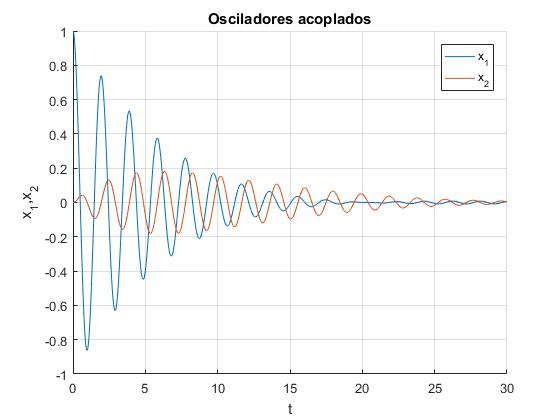
Actividades

Se introduce

• La constante k de los muelles, en el control titulado k muelles
• La constante del muelle k_c que une ambas partículas, en el control titulado k_c acoplamiento
• la masa de las dos partículas se ha fijado en m=1
• La posición inicial de la primera partícula x₀₁, en el control titulado Posición inicial 1.
• Se ha fijado la posición inicial de la segunda partícula x₀₂=0, así como las velocidades iniciales de ambas partículas, v₀₁=0, v₀₂=0

Oscilaciones forzadas

• La constante de amortiguamiento λ, en el control titulado Coeficiente de rozamiento γ
• La frecuencia ω_f de la fuerza oscilante, en el control titulado Frecuencia fuerza ω_f
• La amplitud de la fuerza oscilante se ha fijado en F₀=1

Nota: cuando se establece la constante de amortiguamiento γ=0 y se introduce una frecuencia ω_f de la fuerza oscilante igual a una de las frecuencias de los modos de vibración ω_a o ω_b, el programa genera un error.

Oscilaciones libres o amortiguadas

• Se desactiva la casilla titulada Fuerza oscilante
• Para las oscilaciones libres, la constante de amortiguamiento γ=0

La flecha de color negro debajo de la primera partícula (de color rojo) indica la fuerza oscilante F₀cos(ω_ft) que se aplica a esta partícula

Las flechas de color rojo y de color azul, debajo de las partículas inican la velocidad v₁ de la primera partícula y v₂ de la segunda. Se observará el sentido de las flechas, fuerza y de las velocidades de las partículas cuando la frecuencia ω_f de la fuerza oscilante sea igual a las frecuencias de los modos de vibración ω_a o ω_b,

Se representa, el desplazamiento x₁ de la primera partícula en función del tiempo t, en color rojo y de la segunda x₂ en color azul. Los datos del tiempo t, x₁ y x₂, se proporcionan en la parte superior izquierda

Referencias

M. Ebrahim Foulaadvand, Davoud Masoumi. Mechanical filtering in forced-oscillation of two coupled pendulums. Department of Physics. Shahid Beheshti University (2009)