Consideremos el siguiente sistema de partículas que consta de un muelle en posición horizontal que tiene una masa M en el extremo izquierdo (color azul) y una masa m en su extremo derecho (color rojo).

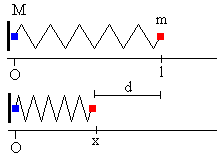
La partícula de masa M está apoyada en una pared vertical. El muelle de constante k y de longitud l sin deformar se comprime una longitud d, de modo que la longitud inicial del muelle es l-d.

Una vez que se suelta el muelle, después de haberse comprimido, observaremos el movimiento de cada partícula y el centro de masas (c.m.) del sistema de dos partículas, que consta de dos etapas:

1. Cuando la partícula de la izquierda de masa M está en contacto con la pared y por tanto, en reposo. El sistema no es aislado, ya que actúa una fuerza exterior, la fuerza N que ejerce la pared sobre dicha partícula.
2. Cuando la partícula de masa M deja de tener contacto con la pared, el sistema es aislado y el centro de masas se mueve con velocidad constante.

Primera etapa del movimiento

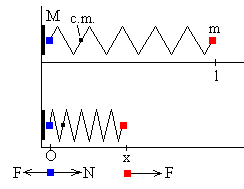
Sobre las partículas del sistema actúan:

• Una fuerza exterior N, la reacción de la pared sobre la cual se apoya la partícula de la derecha.
   
• Las fuerzas de interacción mutua F=k(l-x) iguales y de sentido contrario en cada una de las partículas tal como se muestra en la figura.

Partícula de la derecha (de masa m).

${\displaystyle m\frac{d^{2}x}{d{t}^2}=k(l-x)}$

Esta ecuación se puede escribir

${\displaystyle \frac{d^{2}x}{d{t}^2}+\frac{k}{m}x=\frac{k}{m}l}$

La solución de esta ecuación diferencial, como puede comprobarse por simple sustitución, es de la forma

${\displaystyle x=l+A\sin ({\omega }_{1}t)+B\cos ({\omega }_{1}t){\omega }_1=\sqrt{\frac{k}{m}}}$

Las constantes A y B se calculan a partir de las condiciones iniciales. En el instante t=0, el muelle se ha comprimido una longitud d, la posición de la partícula de la derecha (de masa m) es x=l-d, y su velocidad inicial es dx/dt=0. La posición de dicha partícula en función del tiempo es

x=l-d·cos(ω₁·t)

Derivando respecto del tiempo, obtenemos su velocidad

v_m= d·ω₁·sin(ω₁·t)

Partícula de la izquierda (de masa M)

La partícula de la izquierda está en equilibrio en el origen. La reacción de la pared tal como puede verse en la parte inferior de la figura es

N=k(l-x)=kd·cos(ω₁·t)

Centro de masa (c.m.)

La posición  y velocidad del c.m. son

${\displaystyle z=\frac{mx}{M+m}{v}_{cm}=\frac{m{v}_m}{m+M}}$

Se acaba la primera fase, cuando la partícula de la izquierda (de masa M) deja de tener contacto con la pared, la reacción N es cero. Esto ocurre en el instante t₀ tal que

${\displaystyle \cos ({\omega }_1{t}_0)=0t_0=\frac{\pi }{2{\omega }_1}}$

• La posición de la partícula de la derecha es x=l, su velocidad es v_m=dω₁
• La posición de la partícula de la izquierda es y=0, su velocidad es v_M=0
• La posición y velocidad del c.m. son, respectivamente,

${\displaystyle z_0=\frac{ml}{M+m}{v}_{cm}=\frac{m(d{\omega }_1)}{m+M}}$

Energías

La energía inicial del sistema cuando el muelle está comprimido una longitud d, es kd²/2.

En la situación final:

• el muelle está sin deformar x=l,
• la partícula de la izquierda está en reposo,
• la partícula de la derecha (de masa m) se mueve con velocidad v_m=dω₁

${\displaystyle \frac{1}{2}m{v}_m^2=\frac{1}{2}m{(d{\omega }_1)}^2=\frac{1}{2}m{d}^2\frac{k}{m}=\frac{1}{2}k{d}^2}$

La energía potencial elástica se ha transformado en energía cinética de la partícula de masa m.

Impulso y momento lineal

El momento lineal:

• inicial del sistema es cero
• final del sistema es m·v_m.

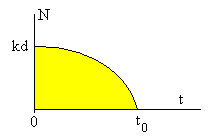
La fuerza exterior N, que ejerce la pared sobre el sistema, actúa durante un tiempo t₀. El impulso de la fuerza N produce un cambio en el momento lineal total del sistema m·v_m.

${\displaystyle {\displaystyle \underset{0}{\overset{t_0}{\int }}N·dt=}{\displaystyle \underset{0}{\overset{t_0}{\int }}kd\cos ({\omega }_{1}t)·dt=}\frac{kd}{{\omega }_1}=\frac{m·{\omega }_1^{2}d}{{\omega }_1}=m{v}_m}$

Segunda etapa del movimiento

En esta fase del movimiento, la fuerza exterior N es nula y sobre cada una de las partículas actúa una fuerza interna F=k(l-(x-y)). Donde (x-y) es la longitud del muelle deformado y l es la longitud del muelle sin deformar. Como no actúa ninguna fuerza exterior sobre el sistema de dos partículas, el sistema es aislado.

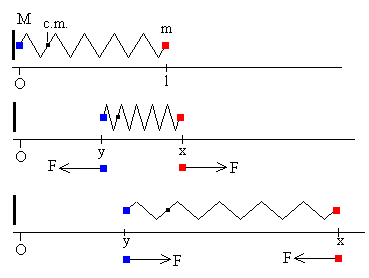
En la figura se muestra:

• en la parte superior, el muelle cuando está sin deformar.
• en la parte intermedia, cuando el muelle está comprimido. Como (x-y) es menor que l, la fuerza F es positiva para la partícula de la derecha (de masa m) y es negativa para la partícula de la izquierda (de masa M).
• en la parte inferior, cuando el muelle está estirado. Como (x-y) es mayor que l, la fuerza F es negativa para la partícula de la derecha (de masa m) y es positiva para la partícula de la izquierda (de masa M).

Las ecuaciones del movimiento para cada una de las dos partículas son,

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=k\left(l-(x-y)\right)\\ M\frac{d^{2}y}{d{t}^2}=-k\left(l-(x-y)\right)\end{array}}$

• Movimiento del centro de masa

Si sumamos las dos ecuaciones tenemos

${\displaystyle m\frac{d^{2}x}{d{t}^2}+M\frac{d^{2}y}{d{t}^2}=0}$

La aceleración del c.m. es cero, el centro de masa se mueve con velocidad constante. Como el sistema formado por las dos partículas es aislado, ya que la fuerza exterior N es nula, la aceleración del c.m. es nula, la velocidad del c.m. es constante e igual a la velocidad inicial en el instante t₀.

${\displaystyle v_{cm}=\frac{m(d{\omega }_1)}{m+M}}$

El movimiento del c.m. es uniforme, su posición es z=z₀+v_cm·(t-t₀), donde z₀ es la posición inicial en el instante t₀ que hemos calculado en el apartado anterior.

${\displaystyle z=\frac{ml}{M+m}+\frac{m(d{\omega }_1)}{m+M}(t-t_0)}$

• Movimiento relativo de las dos partículas

Multiplicando la primera ecuación diferencial por M y la segunda por m y restando ambas ecuaciones diferenciales obtenemos.

${\displaystyle mM\left(\frac{d^{2}x}{d{t}^2}-\frac{d^{2}y}{d{t}^2}\right)=(m+M)k\left(l-(x-y)\right)}$

o bien

${\displaystyle \frac{mM}{m+M}\frac{d^2\xi }{d{t}^2}=k(l-\xi )}$

donde ξ=x-y es la posición relativa de las dos partículas. Esta ecuación nos dice que el movimiento relativo de las dos partículas es equivalente al movimiento de una partícula de masa reducida μ=mM/(m+M) bajo la acción de la fuerza que describe la interacción mutua F=k(l-ξ).

${\displaystyle \frac{d^2\xi }{d{t}^2}+\frac{k}{\mu }\xi =\frac{k}{\mu }l}$

La solución de esta ecuación diferencial, como puede comprobarse por simple sustitución es

${\displaystyle \begin{array}{l}\xi =l+A\sin \left({\omega }_2(t-t_0)\right)+B\cos \left({\omega }_2(t-t_0)\right)\\ {\omega }_2=\sqrt{\frac{k}{\mu }}=\sqrt{\frac{k(m+M)}{mM}}\end{array}}$

Las constantes A y B se determinan a partir de las condiciones iniciales. En el instante t=t₀,

• la posición de las partículas es x=l, y=0, por lo que ξ=x-y=l.
• la velocidad inicial de las partículas es dx/dt=ω₁·d, dy/dt=0, por lo que dξ/dt=ω₁·d

Haciendo algunas operaciones llegamos a

${\displaystyle \xi =l+\frac{{\omega }_{1}d}{{\omega }_2}\sin \left({\omega }_2(t-t_0)\right)}$

Movimiento de cada una de las dos partículas

Conocemos la posición z=(mx+My)/(m+M) del c.m. y la posición relativa ξ=x-y de las partículas en función del tiempo τ=t-t₀.

${\displaystyle \begin{array}{l}z=\frac{mx+My}{m+M}=\frac{ml}{M+m}+\frac{m(d{\omega }_1)}{m+M}\tau \\ \xi =x-y=l+\frac{{\omega }_{1}d}{{\omega }_2}\sin \left({\omega }_2\tau \right)\end{array}}$

Despejamos x e y de este sistema de dos ecuaciones con dos incógnitas

${\displaystyle \begin{array}{l}x=l+\frac{d{\omega }_1}{m+M}\left(m\tau +M\frac{\sin ({\omega }_2\tau )}{{\omega }_2}\right)\\ y=\frac{d{\omega }_1}{m+M}\left(m\tau -m\frac{\sin ({\omega }_2\tau )}{{\omega }_2}\right)\end{array}}$

Comprobamos que en el instante τ=0, (t=t₀) las posiciones iniciales son x=l, y=0.

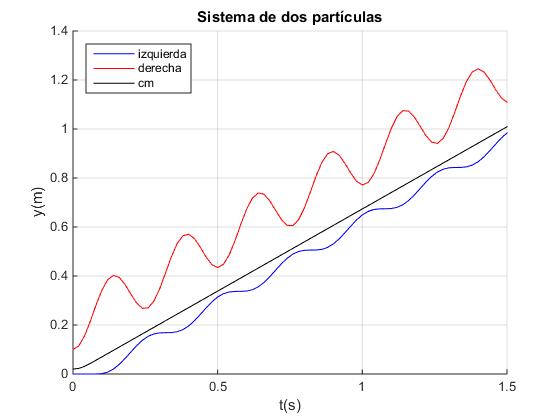
Creamos el siguiente script para representar la posiciones x e y de cada una de las dos partículas y del c.m. z en función del tiempo

k=500;    %constante elástica del muelle
M=4;  %masa izquierda
m=1; %masa derecha
lonMuelle=0.25; %longitud del muelle sin deformar
d=0.15;  %deformación del muelle
w2=sqrt(k*(m+M)/(m*M));
w1=sqrt(k/m);
t0=pi/(2*w1); % tiempo primera etapa

t=0:0.02:1.5;
 x=(lonMuelle-d*cos(w1*t)).*(t<t0)+(lonMuelle+d*w1*(m*(t-t0)+
M*sin(w2*(t-t0))/w2)/(m+M)).*(t0<=t);
 y=(m*d*w1*((t-t0)-sin(w2*(t-t0))/w2)/(m+M)).*(t0<=t);
 z=(m*x+M*y)/(m+M);  %centro de masa

hold on
plot(t,y,'blue')
plot(t,x,'red')
plot(t,z,'black')
hold off
legend('izquierda','derecha','cm','Location','northwest')
xlabel('t(s)')
ylabel('y(m)')
title('Sistema de dos partículas')
grid on

Las velocidades de las partículas en cualquier instante τ=t-t₀ son

${\displaystyle \begin{array}{l}\frac{dx}{d\tau }=\frac{d{\omega }_1}{m+M}\left(m+M\text{cos}({\omega }_2\tau )\right)\\ \frac{dy}{d\tau }=\frac{d{\omega }_1}{m+M}\left(m-m\text{cos}({\omega }_2\tau )\right)\end{array}}$

Comprobamos que en el instante τ=0, (t=t₀), las velocidades iniciales son  dx/dτ =ω₁·d, dy/dτ=0

Energías:

La energía cinética de las partículas es

${\displaystyle E_k=\frac{1}{2}m{\left(\frac{dx}{d\tau }\right)}^2+\frac{1}{2}M{\left(\frac{dy}{d\tau }\right)}^2=\frac{1}{2}\frac{{(d{\omega }_1)}^2}{m+M}\left(m^2+mM{\cos }^2({\omega }_2\tau )\right)}$

Como la deformación del muelle es l-(x-y). La energía potencial de interacción entre las dos partículas es

${\displaystyle E_p=\frac{1}{2}k{\left(l-(x-y)\right)}^2=\frac{1}{2}\frac{{(d{\omega }_1)}^2}{m+M}mM{\sin }^2({\omega }_2\tau )}$

La energía total U del sistema de partículas es la suma de ambas contribuciones

${\displaystyle U=E_k+E_p=\frac{1}{2}\frac{{(d{\omega }_1)}^2}{m+M}(m^2+mM)=\frac{1}{2}k{d}^2}$

que es la energía inicial del muelle comprimido una longitud d.

Como el trabajo de la fuerza exterior N es cero (ya que la partícula de masa M no se desplaza mientras N es distinto de cero), la energía U del sistema de dos partículas unidas por un muelle elástico permanece constante, e igual a la energía inicial.

La energía inicial del muelle comprimido una longitud d, se transforma en energía cinética de la partícula de masa m cuando finaliza la primera etapa del movimiento, y en energía cinética y potencial del sistema aislado formado por las dos partículas unidas por un muelle elástico.

Actividades

Se introduce

• La masa m de la partícula situada a la derecha (en color rojo) en el control titulado Masa derecha.
• La masa M de la partícula situada a la izquierda (en color azul), en el control titulado Masa izquierda.
• La constante k del muelle elástico, en el control titulado Cte. muelle.
• La longitud l del muelle sin deformar está fijada por el programa interactivo en l=0.25 m

Se pulsa el botón titulado Nuevo.

Actuando con el puntero del ratón sobre la partícula de color rojo, comprimimos el muelle una longitud d. (situación inicial)

Observamos el movimiento de las dos partículas (roja y azul) y la del centro de masa del sistema (en color negro). En la parte superior, se representa su posición de cada partícula y del c.m. en función del tiempo t.

Distinguimos las dos etapas del movimiento:

1. En la primera etapa, la partícula de la izquierda está en reposo en contacto con la pared vertical. Una flecha de color negro, señala la fuerza exterior N, que ejerce la pared sobre el sistema.
2. En la segunda etapa, el sistema es aislado, observamos el movimiento de las partículas bajo la acción de su interacción mutua.

Ejemplo:

• La masa de la partícula de la derecha m=1 kg
• la masa de la partícula de la izquierda M=4 kg
• la constante elástica del muelle k=500 N/m

Se comprime el muelle una distancia d=0.15 m, hasta que la posición de la partícula de la derecha x=0.1 m.

Al cabo de un tiempo t₀ la partícula de la derecha deja de tener contacto con la pared N=0.

${\displaystyle {\omega }_1=\sqrt{\frac{500}{1}}=22.36\text{rad/s}{t}_0=\frac{\pi }{2·22.36}=0.07\text{s}}$

En dicho instante, la posición:

• de la partícula de la derecha es x=0.25,
• la de la izquierda es y=0.0.
• del centro de masa es $z=\frac{1·0.25}{1+4}=0.05\text{m}$

La velocidad:

• de la partícula de la derecha es v_m=dω₁=0.15·22.36=3.35 m/s
• de la partícula de la izquierda es v_M=0
• del centro de masas es $v_{cm}=\frac{1·3.35}{1+4}=0.67\text{m/s}$

Esta es la velocidad constante del c.m. del sistema en la segunda etapa del movimiento.

La energía del sistema de partículas es $U=\frac{1}{2}k{d}^2=\frac{1}{2}500·{0.15}^2=5.63\text{J}$ que es constante.

Se pulsa el botón Nuevo, con el puntero del ratón se arrastra el pequeño cuadrado de color rojo para comprimir el muelle. Se suelta y se observa el movimiento del sistema de dos partículas unidas por el muelle.