El ojo de pez de Maxwell

En este caso, el índice de refracción n varía con la distancia radial r, n=n(r). Para que el tiempo sea mínimo, tenemos que calcular el extremo de la funcional

${\displaystyle \begin{array}{l}I={\displaystyle \underset{A}{\overset{B}{\int }}n(r)\sqrt{d{r}^2+r^{2}d{\theta }^2}}={\displaystyle \underset{A}{\overset{B}{\int }}n(r)\sqrt{1+r^2{\left(\frac{d\theta }{dr}\right)}^2}dr}\\ ={\displaystyle \underset{A}{\overset{B}{\int }}n(r)\sqrt{1+r^2{\dot{\theta }}^2}dr}\end{array}}$

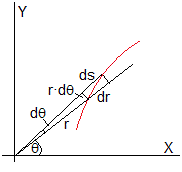
La función f es

${\displaystyle f(r)=n(r)\sqrt{1+r^2{\dot{\theta }}^2}}$

Aplicamos la ecuación de Euler-Lagrange

${\displaystyle \frac{\partial f}{\partial \theta }-\frac{d}{dr}\left(\frac{\partial f}{\partial \dot{\theta }}\right)=0}$

Como f no depende de θ, tenemos

${\displaystyle \begin{array}{l}\frac{\partial f}{\partial \dot{\theta }}=c\\ \frac{r^{2}n(r)\dot{\theta }}{\sqrt{1+r^2{\dot{\theta }}^2}}=c\\ \frac{d\theta }{dr}=\frac{c}{r\sqrt{r^2{n}^2-c^2}}\end{array}}$

Supongamos que el índice de refracción n(r) depende de la distancia radial r

${\displaystyle n(r)=\frac{n_0}{1+{\left(\frac{r}{a}\right)}^2}}$

Haciendo el cambio de variable

${\displaystyle \rho =\frac{r}{a},\alpha =\frac{c}{n_{0}a}}$

Obtenemos

${\displaystyle d\theta =\frac{\alpha \left(1+{\rho }^2\right)}{\rho \sqrt{{\rho }^2-{\alpha }^2{\left(1+{\rho }^2\right)}^2}}d\rho }$

Integramos para obtener la ecuación θ=θ(r) de los rayos dependiente de dos constantes de integración c o α y θ₁

${\displaystyle \begin{array}{l}\theta ={\displaystyle \int \frac{\alpha \left(1+{\rho }^2\right)}{\rho \sqrt{{\rho }^2-{\alpha }^2{\left(1+{\rho }^2\right)}^2}}d\rho +{\theta }_1}\\ \theta =\arcsin \left(\frac{\alpha }{\sqrt{1-4{\alpha }^2}}\frac{{\rho }^2-1}{\rho }\right)+{\theta }_1\\ \sin \left(\theta -{\theta }_1\right)=\frac{c}{\sqrt{n_0^2{a}^2-4c^2}}\frac{r^2-a^2}{ra}\end{array}}$

El resultado de la integral, que el lector puede verificar derivando el arcsin, se ha tomado del texto de Max Born y Emil Wolf, véase las Referencias

Se determina la constante c sabiendo que los rayos parten del punto de coordenadas polares (r₀, θ₀)

${\displaystyle \begin{array}{l}\sin \left({\theta }_0-{\theta }_1\right)=\frac{c}{\sqrt{n_0^2{a}^2-4c^2}}\frac{r_0^2-a^2}{r_{0}a}\\ c^2=\frac{n_0^2{a}^4{\sin }^2\left({\theta }_0-{\theta }_1\right)}{{\left(r_0^2-a^2\right)}^2+4r_0^2{a}^2{\sin }^2\left({\theta }_0-{\theta }_1\right)}\end{array}}$

La ecuación de los rayos que depende de la constante de integración θ₁ es

${\displaystyle \frac{r\sin \left(\theta -{\theta }_1\right)}{r^2-a^2}=\frac{r_0\sin \left({\theta }_0-{\theta }_1\right)}{r_0^2-a^2}}$

Volviendo a las coordenadas rectangulares, x=rcosθ, y=rsinθ, comprobamos se trata de la ecuación de una circunferencia, calculamos su centro y radio

${\displaystyle \begin{array}{l}r\sin \theta \cos {\theta }_1-r\cos \theta \sin {\theta }_1=\frac{r_0\sin \left({\theta }_0-{\theta }_1\right)}{r_0^2-a^2}\left(x^2+y^2-a^2\right)\\ x^2+y^2-\frac{1}{b}y\cos {\theta }_1+\frac{1}{b}x\sin {\theta }_1=a^2,b=\frac{r_0\sin \left({\theta }_0-{\theta }_1\right)}{r_0^2-a^2}\\ {\left(x+\beta \sin {\theta }_1\right)}^2+{\left(y-\beta \cos {\theta }_1\right)}^2=a^2+{\beta }^2,\beta =\frac{1}{2b}\\ {\left(x-x_c\right)}^2+{\left(y-y_c\right)}^2=R^2,\{\begin{array}{l}{x}_c=-\frac{\sin {\theta }_1}{2b}\\ y_c=\frac{\cos {\theta }_1}{2b}\\ R=\sqrt{a^2+\frac{1}{4b^2}}\end{array}\end{array}}$

Representamos la ecuación de los rayos que pasan por la posición r₀=0.5, y θ₀=π/6, para los siguientes valores de la constante θ₁=-0.1, 0, 0.1, 0.2. Se toma el parámetro a=1

a=1;
r0=0.5; %posición de partida
th_0=pi/6;
hold on
for th1=[-0.1, 0, 0.1, 0.2]
    b=r0*sin(th_0-th1)/(r0^2-a^2);
    R=sqrt(a^2+1/(4*b^2)); %radio
    xC=-sin(th1)/(2*b); %centro
    yC=cos(th1)/(2*b);
    fplot(@(t) xC+R*cos(t), @(t) yC+R*sin(t), [0,2*pi],'displayName',num2str(th1))
end
hold off
grid on
axis equal
legend('-DynamicLegend','location','best')
xlabel('x')
ylabel('y')
title('Ojo de pez de Maxwell')

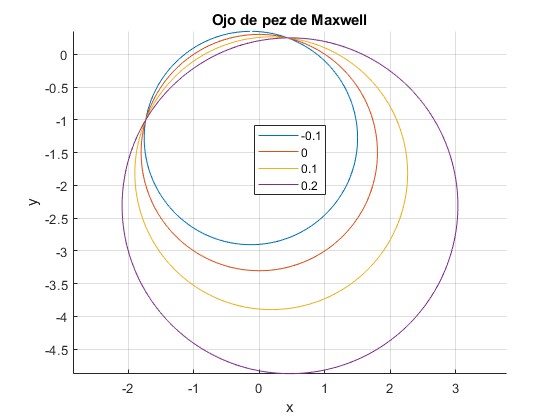
Actividades

Se introduce

• El valor de la constante θ₁ en el control titulado Constante
• Los rayos pasan por una posición que se ha fijado en r₀=0.5, y θ₀=π/6
• Se ha fijado el parámetro a=1

Se pulsa el botón titulado Nuevo

El fondo (en color que va de negro a gris claro) nos muestra el índice de refracción, que va disminuyendo a medida que nos alejamos radialmente del origen

Representamos la trayectoria circular de la luz que pasa por el punto r₀=0.5, y θ₀=π/6, señalado por un punto de color azul claro

Simulación de una lente gravitacional

En este caso, el índice de refracción n varía con la distancia de la forma

${\displaystyle n^2(r)=1+\frac{C^2}{r^2}}$

donde C es una constante

Para que el tiempo sea mínimo, tenemos que calcular el extremo de la funcional

${\displaystyle I={\displaystyle \underset{A}{\overset{B}{\int }}n(r)}\sqrt{d{r}^2+r^{2}d\theta }={\displaystyle \underset{A}{\overset{B}{\int }}n(r)\sqrt{{\left(\frac{dr}{d\theta }\right)}^2+r^2}·d\theta }={\displaystyle \underset{A}{\overset{B}{\int }}n(r)\sqrt{{\dot{r}}^2+r^2}·d\theta }}$

La función f es

${\displaystyle f(r,\dot{r},\theta )=n\sqrt{{\dot{r}}^2+r^2}}$

Aplicamos la ecuación de Euler-Lagrange

${\displaystyle \frac{\partial f}{\partial r}-\frac{d}{d\theta }\left(\frac{\partial f}{\partial \dot{r}}\right)=0}$

El resultado es

${\displaystyle \begin{array}{l}\frac{dn}{dr}\sqrt{{\dot{r}}^2+r^2}+\frac{nr}{\sqrt{{\dot{r}}^2+r^2}}-\frac{d}{d\theta }\left(\frac{n\dot{r}}{\sqrt{{\dot{r}}^2+r^2}}\right)=0\\ \frac{dn}{dr}\sqrt{{\dot{r}}^2+r^2}+\frac{nr}{\sqrt{{\dot{r}}^2+r^2}}-\left(\frac{dn}{dr}\frac{dr}{d\theta }\right)\frac{\dot{r}}{\sqrt{{\dot{r}}^2+r^2}}-n\frac{d^{2}r}{d{\theta }^2}\frac{1}{\sqrt{{\dot{r}}^2+r^2}}+n\dot{r}\frac{\dot{r}\frac{d^{2}r}{d{\theta }^2}+r\frac{dr}{d\theta }}{{\left({\dot{r}}^2+r^2\right)}^{3/2}}=0\\ \frac{dn}{dr}\left({\dot{r}}^2+r^2\right)+nr-\frac{dn}{dr}{\dot{r}}^2-n\ddot{r}+n\dot{r}\frac{\dot{r}\ddot{r}+r\dot{r}}{{\dot{r}}^2+r^2}=0\\ r^2\frac{dn}{dr}+n\left(r-\ddot{r}+\frac{{\dot{r}}^2\ddot{r}+r{\dot{r}}^2}{{\dot{r}}^2+r^2}\right)=0\\ r^2\frac{dn}{dr}+n\left(\frac{r^3+2r{\dot{r}}^2-r^2\ddot{r}}{{\dot{r}}^2+r^2}\right)=0\end{array}}$

Tenemos que resolver la ecuación diferencial

${\displaystyle \frac{n\text{'}(r)}{n(r)}+\frac{r^2+2{\dot{r}}^2-r\ddot{r}}{r\left({\dot{r}}^2+r^2\right)}=\mathrm{0,}n\text{'}=\frac{dn}{dr},\dot{r}=\frac{dr}{d\theta },\ddot{r}=\frac{d^{2}r}{d{\theta }^2}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}u(r)=\frac{\dot{r}}{r},\frac{dr}{d\theta }=r·u\\ \ddot{r}=\frac{d^{2}r}{d{\theta }^2}=\frac{d}{d\theta }\left(\frac{dr}{d\theta }\right)=\frac{d}{dr}\left(\frac{dr}{d\theta }\right)\frac{dr}{d\theta }=\dot{r}\frac{d\dot{r}}{dr}=\dot{r}\frac{d}{dr}\left(r·u\right)=ur\left(u+r\frac{du}{dr}\right)=u^{2}r+r^{2}uu\text{'}\\ \frac{n\text{'}}{n}+\frac{r^2+2{\dot{r}}^2-r\ddot{r}}{r\left({\dot{r}}^2+r^2\right)}=0\\ \frac{n\text{'}}{n}+\frac{r^2+2r^2{u}^2-r\left(u^{2}r+r^{2}uu\text{'}\right)}{r\left(r^2{u}^2+r^2\right)}=0\\ \frac{n\text{'}}{n}+\frac{1+u^2-ruu\text{'}}{r\left(u^2+1\right)}=0\\ \frac{n\text{'}}{n}+\frac{1}{r}-\frac{uu\text{'}}{u^2+1}=0\end{array}}$

Integramos con respecto de r

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{dn}{n}}+{\displaystyle \int \frac{dr}{r}}-{\displaystyle \int \frac{u}{u^2+1}du}=B\text{'}\\ \ln (n)+\ln (r)-\frac{1}{2}\ln \left(u^2+1\right)=B\text{'}\\ \frac{r·n}{\sqrt{1+u^2(r)}}=B\\ B\sqrt{1+\frac{1}{r^2}{\left(\frac{dr}{d\theta }\right)}^2}=r·n,B\sqrt{r^2+{\dot{r}}^2}=r^{2}n\\ 1+\frac{1}{r^2}{\left(\frac{dr}{d\theta }\right)}^2=\frac{r^2{n}^2}{B^2}\\ \frac{dr}{d\theta }=\frac{r}{B}\sqrt{r^2{n}^2-B^2}\\ B{\displaystyle \int \frac{dr}{r\sqrt{r^2{n}^2-B^2}}}=\theta -{\theta }_0\end{array}}$

donde θ₀ es una constante de integración

Para el índice de refracción

${\displaystyle \begin{array}{l}{n}^2(r)=1+\frac{C}{r^2}\\ B{\displaystyle \int \frac{dr}{r\sqrt{r^2\left(1+\frac{C^2}{r^2}\right)-B^2}}}=\theta -{\theta }_0\\ B{\displaystyle \int \frac{dr}{r\sqrt{r^2+C^2-B^2}}}=\theta -{\theta }_0\end{array}}$

La integral produce dos resultados distintos

• Si B>C tenemos una integral del tipo

${\displaystyle {\displaystyle \int \frac{dx}{x\sqrt{x^2-a^2}}}}$

con a²=B²-C². Haciendo el cambio de variable

${\displaystyle \begin{array}{l}t=\frac{1}{x},dt=\frac{-dx}{x^2},dx=-\frac{1}{t^2}dt\\ {\displaystyle \int \frac{dx}{x\sqrt{x^2-a^2}}}=-{\displaystyle \int \frac{\frac{1}{t^2}dt}{\frac{1}{t}\sqrt{\frac{1}{t^2}-a^2}}=-{\displaystyle \int \frac{dt}{\sqrt{1-t^2{a}^2}}}}\end{array}}$

Llamando u=at, du=a·dt

${\displaystyle {\displaystyle \int \frac{dx}{x\sqrt{x^2-a^2}}}=-\frac{1}{a}{\displaystyle \int \frac{du}{\sqrt{1-u^2}}}=-\frac{1}{a}\arcsin u=-\frac{1}{a}\arcsin \left(at\right)=-\frac{1}{a}\arcsin \left(\frac{a}{x}\right)}$

• Si C>B tenemos una integral del tipo

${\displaystyle {\displaystyle \int \frac{dx}{x\sqrt{x^2+a^2}}}}$

con a²=C²-B². Haciendo el cambio de variable

${\displaystyle \begin{array}{l}t=\frac{1}{x},dt=\frac{-dx}{x^2},dx=-\frac{1}{t^2}dt\\ {\displaystyle \int \frac{dx}{x\sqrt{x^2+a^2}}}=-{\displaystyle \int \frac{\frac{1}{t^2}dt}{\frac{1}{t}\sqrt{\frac{1}{t^2}+a^2}}=-{\displaystyle \int \frac{dt}{\sqrt{1+t^2{a}^2}}}}\end{array}}$

Llamando u=at, du=a·dt

${\displaystyle {\displaystyle \int \frac{dx}{x\sqrt{x^2+a^2}}}=-\frac{1}{a}{\displaystyle \int \frac{du}{\sqrt{1+u^2}}}=-\frac{1}{a}\text{arcsinh(}u)=-\frac{1}{a}\text{arcsinh}\left(at\right)=-\frac{1}{a}\text{arcsinh}\left(\frac{a}{x}\right)}$

Deshaciendo los cambios, el resultado es

• B>C

${\displaystyle \begin{array}{l}-\frac{B}{\sqrt{B^2-C^2}}\arcsin \left(\frac{\sqrt{B^2-C^2}}{r}\right)=\theta -{\theta }_0\\ r=-\frac{\sqrt{B^2-C^2}}{\sin \left(\frac{\sqrt{B^2-C^2}}{B}\left(\theta -{\theta }_0\right)\right)}\end{array}}$

• C>B

${\displaystyle \begin{array}{l}-\frac{B}{\sqrt{C^2-B^2}}\text{arcsinh}\left(\frac{\sqrt{C^2-B^2}}{r}\right)=\theta -{\theta }_0\\ r=-\frac{\sqrt{C^2-B^2}}{\sinh \left(\frac{\sqrt{C^2-B^2}}{B}\left(\theta -{\theta }_0\right)\right)}\end{array}}$

Tomamos C=1, θ₀=0 y representamos los caminos que sigue la luz para B=0.8, 1.5

C=1; %constante
hold on
 for B=[0.8,1.5]
    if B>C
       r=@(x) sqrt(B^2-C^2)./sin(sqrt(B^2-C^2)*x/B);
       fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x),[0.1,pi*(1-1/100)*B
/sqrt(B^2-C^2)])
    else
        r=@(x) sqrt(C^2-B^2)./sinh(sqrt(C^2-B^2)*x/B);
        fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x),[0.1,10*pi])
    end
end
hold off
xlim([-4,4])  
ylim([-4,4])
grid on
legend('0.8','1.5','location', 'best')
xlabel('x')
ylabel('y')
title('Lente gravitatoria')

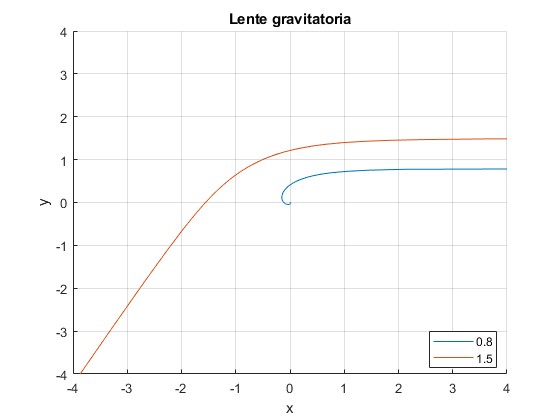
Para B<C la luz termina en el origen. Para B>C la luz cambia de dirección

Representamos los caminos que sigue la luz para varios valores de B

C=1; %constante
hold on
 for B=0.5:0.1:1.95
    if B>C
       r=@(x) sqrt(B^2-C^2)./sin(sqrt(B^2-C^2)*x/B);
      fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x),[0.1,pi*(1-1/100)*B
/sqrt(B^2-C^2)])
    else
        r=@(x) sqrt(C^2-B^2)./sinh(sqrt(C^2-B^2)*x/B);
        fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x),[0.1,10*pi])
    end
end
hold off
xlim([-4,4])  
ylim([-4,4])
grid on
xlabel('x')
ylabel('y')
title('Lente gravitatoria')

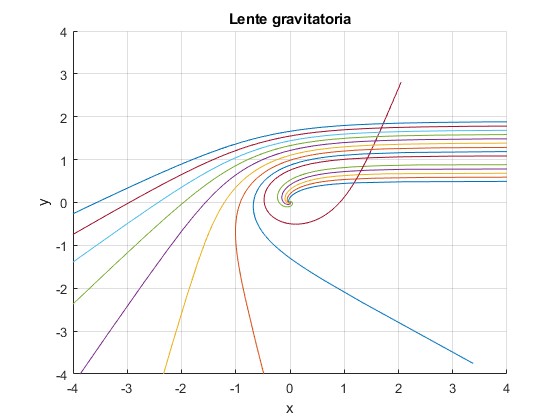
• Para B>C

La trayectoria se describe haciendo que el argumento de seno cambie de 0 a π. Para θ=0, r→∞ y cuando $\frac{\sqrt{B^2-C^2}}{B}\theta =\pi$, r→∞

θ₁=0, es el ángulo de entrada y ${\theta }_2=\frac{B}{\sqrt{B^2-C^2}}\pi$, es el ángulo de salida

La distancia d más próxima al origen se produce cuando el seno vale la unidad, $d=\sqrt{B^2-C^2}$

Las trayectorias más interesantes se obtienen para B≈C=1. Así, valores de B algo mayores que C producen trayectorias que dan vueltas alrededor del origen antes de alejarse al infinito

C=1; %constante
B=1.025;
r=@(x) sqrt(B^2-C^2)./sin(sqrt(B^2-C^2)*x/B);
fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x),[0.1,pi*(1-1/100)*B/
sqrt(B^2-C^2)])
xlim([-4,4])  
ylim([-4,4])
grid on
xlabel('x')
ylabel('y')
title('Lente gravitatoria')



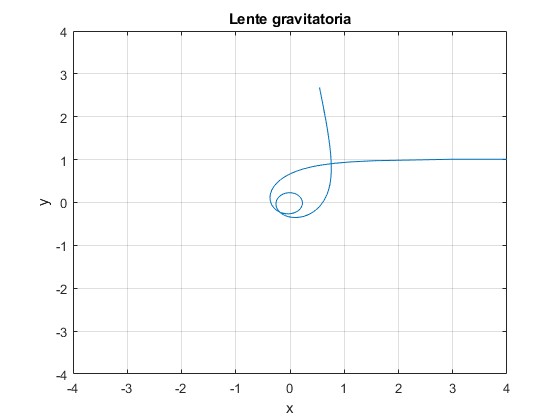
• Para B<C

La trayectoria viene descrita por la funcion seno hiperbólico cuyo argumento varía entre θ=0 (r→∞), entrada y θ→∞ (r→0), terminando en el origen

Tiempo que tarda la luz en recorrer una porción de camino

Una porción diferencial de camino de la luz es

${\displaystyle dL=n(r)\sqrt{r^2+{\dot{r}}^2}·d\theta }$

Teniendo en cuenta la relación deducida en el apartado anterior

${\displaystyle \begin{array}{l}B\sqrt{r^2+{\dot{r}}^2}=r^2·n\\ dL=\frac{1}{B}{n}^2{r}^{2}d\theta \end{array}}$

Si c es la velocidad de la luz en el vacío

${\displaystyle \begin{array}{l}c·dt=\frac{1}{B}{n}^2{r}^2\omega ·dt\\ Bc=n^2{r}^2\omega \end{array}}$

Anteriormente, hemos obtenido y representado la ecuación del camino que sigue la luz

${\displaystyle \begin{array}{l}B{\displaystyle \int \frac{dr}{r\sqrt{r^2{n}^2-B^2}}}=\theta -{\theta }_0,B\frac{dr}{r\sqrt{r^2{n}^2-B^2}}=d\theta ,\\ B\frac{dr}{r\sqrt{r^2{n}^2-B^2}}=\omega dt,B\frac{dr}{r\sqrt{r^2{n}^2-B^2}}=\frac{Bc}{n^2{r}^2}dt\\ dt=\frac{1}{c}\frac{r{n}^2}{\sqrt{r^2{n}^2-B^2}}dr\end{array}}$

Integrando para una expresión particular del índice de refracción, n(r), obtenemos el tiempo que tarda la luz en ir desde una posición a otra

Referencias

Max Born, Emil Wolf. Principles of Optics. Electromagnetic Theory of Propagation, Interference and Diffraction of Light. Cambridge University Press. Seventh edition. pp. 157-159

Bogdan Szafraniec, James F. Harford. A simple model of a gravitational lens from geometric optics. Am. J. Phys. 92 (11), November 2024. pp. 878-884