Péndulo cónico simple

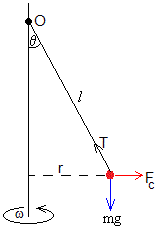
Supongamos una partícula de masa m que está conectada mediante una varilla rígida de longitud l y de masa despreciable al eje vertical de un motor en O. La varilla se desvía del eje vertical un ángulo θ cuando la velocidad angular del motor ω es mayor que un cierto valor crítico ω_c. La partícula describe entonces una circunferencia horizontal de radio l·sinθ.

En el Sistema de Referencia en rotación con velocidad angular ω, las fuerzas que actúan sobre la partícula son

• El peso, mg
• La fuerza centrífuga, mω²r
• La tensión de la varilla, T

Las ecuaciones del equilibrio de la partícula establecen la relación entre el ángulo θ y la velocidad angular de rotación ω

${\displaystyle \begin{array}{l}\{\begin{array}{l}T\sin \theta =m{\omega }^{2}r\\ T\cos \theta =mg\end{array}\\ T=m{\omega }^{2}l\\ \cos \theta =\frac{g}{{\omega }^{2}l}\end{array}}$

Para que cosθ≤1, ω²≥g/l. Donde g/l es el cuadrado de la velocidad angular crítica ω_c

El punto de sujección O dista d del eje de rotación

Primer modo de rotación, θ>0

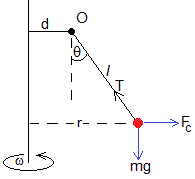
Las ecuaciones del equilibrio de la partícula establecen la relación entre el ángulo θ y la velocidad angular de rotación ω

${\displaystyle \begin{array}{l}\{\begin{array}{l}T\sin \theta =m{\omega }^{2}r\\ T\cos \theta =mg\end{array}\\ \tan \theta =\frac{{\omega }^{2}r}{g}\\ {\omega }^2=\frac{g\tan \theta }{l\sin \theta +d}=\frac{g}{l}\frac{\tan \theta }{\sin \theta +\frac{d}{l}}\\ \frac{{\omega }^2}{{\omega }_c^2}=\frac{\tan \theta }{\sin \theta +\frac{d}{l}}\end{array}}$

Segundo modo de rotación, θ<0

${\displaystyle \begin{array}{l}\{\begin{array}{l}T\sin \theta =m{\omega }^{2}r\\ T\cos \theta =mg\end{array}\\ \tan \theta =\frac{{\omega }^{2}r}{g}\\ {\omega }^2=\frac{g\tan \theta }{l\sin \theta -d}=\frac{g}{l}\frac{\tan \theta }{\sin \theta -\frac{d}{l}}\\ \frac{{\omega }^2}{{\omega }_c^2}=\frac{\tan \theta }{\sin \theta -\frac{d}{l}}\end{array}}$

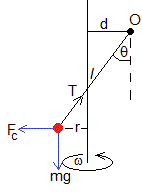
La misma fórmula vale para ambos modos de rotación

${\displaystyle \frac{{\omega }^2}{{\omega }_c^2}=\frac{\tan \theta }{\sin \theta +\frac{d}{l}},\{\begin{array}{l}\theta >\mathrm{0,}\text{primer modo}\\ \theta <\mathrm{0,}\text{segundo modo}\end{array}}$

Representamos la velocidad angular ω/ω_c en función del ángulo de desviación θ para varios valores de la distancia d=0, 0.01, 0.05, 0.1 m. La longitud del péndulo cónico es l=0.2 m

l=0.2; %longitud del péndulo
hold on
for d=[0,0.01,0.05,0.1] %th>0
    fplot(@(x) sqrt(tan(x)./(sin(x)+d/l)),[0,pi/3])
end
for d=[0.01,0.05,0.1] %th<0
    f=@(x) sqrt(tan(x)./(sin(x)+d/l));
    fplot(f,[-pi/3,0])
    th_m=-asin((d/l)^(1/3));
    plot(th_m,f(th_m), 'ko','markersize',3,'markerfacecolor','k')
end
hold off
set(gca,'XTick',-pi/3:pi/12:pi/3)
set(gca,'XTickLabel',{'-\pi/3','-\pi/4','-\pi/6', '-\pi/12', '0','\pi/12',
'\pi/6','\pi/4','\pi/3'})
grid on
ylim([0,3])
xlim([-pi/3,pi/3])
ylabel('\omega/\omega_c')
xlabel('\theta')
title('Péndulo cónico simple')

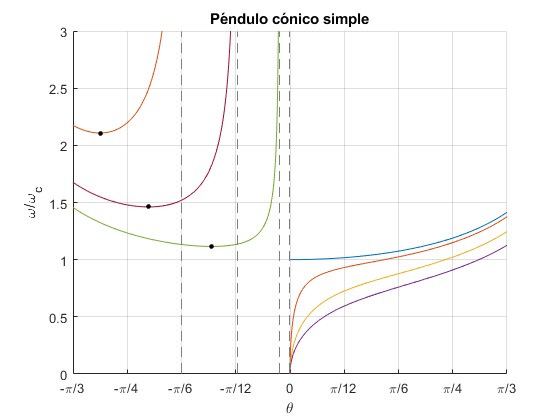
A la izquierda en la figura, θ<0, tenemos el segundo modo de rotación y a la derecha, θ>0, el primer modo de rotación, las velocidades angulares ω/ω_c del primer modo son menores que las del segundo

En la parte derecha, la curva de color azul corresponde a d=0, el punto de sujección O está en el eje de giro. El péndulo se desvía θ>0, para ω>ω_c, o bien, ω/ω_c>1. Cuando el punto O de sujección del péndulo está a una distancia d, la desviación del péndulo θ>0 se incrementa con la velocidad angular ω

Para el segundo modo, θ<0, la función ω(θ) presenta un mínimo señalado por un punto de color negro. Calculamos el ángulo θ_m derivando la función ω(θ) respecto de θ e igualando a cero.

${\displaystyle \begin{array}{l}\frac{d}{d\theta }\left(\frac{\tan \theta }{\sin \theta +\frac{d}{l}}\right)=0\\ \frac{1}{{\cos }^2\theta }\left(\sin \theta +\frac{d}{l}\right)-\tan \theta \cos \theta =0\\ {\sin }^3\theta =-\frac{d}{l},\theta <0\end{array}}$

Péndulo cónico doble

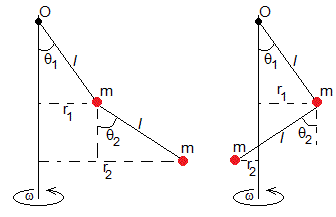
Un péndulo cónico doble, consta de una varilla rígida de longitud l y de masa despreciable sujeta por uno de sus extremos al eje de rotación, se fija al otro extremo una partícula de masa m. En esta partícula se fija el extremo del segundo péndulo cónico de las mismas dimensiones

En la figura, se muestra los dos modos de rotación.

• Primer modo, θ₂>0
• Segundo modo, θ₂<0

Las velocidades angulares ω del primer modo son menores que las del segundo, tal como veremos al final de este apartado

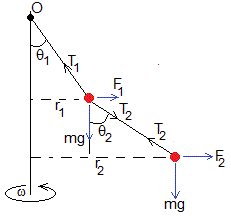
En la figura, se muestran las fuerzas sobre cada una de las dos partículas, T₁ y T₂ son las tensiones de las varillas y F₁=mω²r₁ y F₂=mω²r₂, las fuerzas centrífugas.

• Equilibrio de la segunda partícula

${\displaystyle \begin{array}{l}\{\begin{array}{l}{T}_2\sin {\theta }_2=m{\omega }^2{r}_2\\ T_2\cos {\theta }_2=mg\end{array}\\ \tan {\theta }_2=\frac{{\omega }^2{r}_2}{g}\\ {\omega }^2=\frac{g\tan {\theta }_2}{l\sin {\theta }_1+l\sin {\theta }_2}\\ \frac{{\omega }^2}{{\omega }_c^2}=\frac{\tan {\theta }_2}{\sin {\theta }_1+\sin {\theta }_2}\end{array}}$

• Equilibrio de la primera partícula

${\displaystyle \begin{array}{l}\{\begin{array}{l}{T}_1\sin {\theta }_1=m{\omega }^2{r}_1+T_2\sin {\theta }_2\\ T_1\cos {\theta }_1=mg+T_2\cos {\theta }_2\end{array}\\ \tan {\theta }_1=\frac{{\omega }^2\left(r_1+r_2\right)}{2g}\\ \frac{{\omega }^2}{{\omega }_c^2}=\frac{2\tan {\theta }_1}{2\sin {\theta }_1+\sin {\theta }_2}\end{array}}$

Dado θ₂ calculamos θ₁ resolviendo la ecuación trascendente

${\displaystyle \frac{\tan {\theta }_2}{\sin {\theta }_1+\sin {\theta }_2}=\frac{2\tan {\theta }_1}{2\sin {\theta }_1+\sin {\theta }_2}}$

Dado el ángulo θ₂ calculamos θ₁, utilizando la función fzero de MATLAB y con ambos ángulos, calculamos la velocidad angular de rotación ω/ω_c. Representamos la velocidad angular ω/ω_c en función del ángulo θ₂

hold on
ang_2=(0:80)*pi/180;
w=zeros(1,length(ang_2));
i=1;
for th_2=ang_2 %th_2>0
    f=@(x) tan(th_2)*(2*sin(x)+sin(th_2))-2*tan(x)*(sin(x)+sin(th_2));
    th_1=fzero(f,[0,pi/2]);
    w(i)=sqrt(tan(th_2)/(sin(th_1)+sin(th_2)));
    i=i+1;
end
plot(ang_2,w)
ang_2=-(0:80)*pi/180; %th_2<0
w=zeros(1,length(ang_2));
i=1;
for th_2=ang_2
    f=@(x) tan(th_2)*(2*sin(x)+sin(th_2))-2*tan(x)*(sin(x)+sin(th_2));
    th_1=fzero(f,[0, pi/2]);
    w(i)=sqrt(tan(th_2)/(sin(th_1)+sin(th_2)));
    i=i+1;
end
plot(ang_2,w)
hold off
set(gca,'XTick',-5*pi/12:pi/12:5*pi/12)
set(gca,'XTickLabel',{'-5\pi/12','-\pi/3','-\pi/4','-\pi/6', '-\pi/12', '0',
'\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12'})
grid on
ylim([0,4])
ylabel('\omega/\omega_c')
xlabel('\theta_2')
title('Péndulo cónico doble')

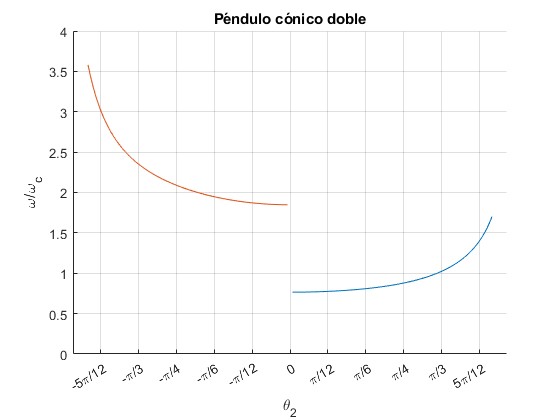
En la figura, apreciamos que la velocidad angular de rotación ω/ω_c es mayor para el segundo modo θ₂<0, que para el primero θ₂>0,

Dada la velocidad angular de rotación ω/ω_c, obtenemos θ₁ y θ₂ resolviendo el sistema de dos ecuaciones no lineales

${\displaystyle \{\begin{array}{l}\frac{{\omega }^2}{{\omega }_c^2}\left(\sin {\theta }_1+\sin {\theta }_2\right)-\tan {\theta }_2=0\\ \frac{{\omega }^2}{{\omega }_c^2}\left(2\sin {\theta }_1+\sin {\theta }_2\right)-2\tan {\theta }_1=0\end{array}}$

La solución gráfica para ω/ω_c=1 es

w2=1^2; %cuadrado de la velocidad angular de rotación
hold on
f=@(x,y) w2*(sin(x)+sin(y))-tan(y);
fimplicit(f,[-pi/3,pi/3, -pi/3, pi/3])
f=@(x,y) w2*(2*sin(x)+sin(y))-2*tan(x);
fimplicit(f,[-pi/3,pi/3, -pi/3, pi/3])
grid on
xlabel('x')
ylabel('y')
title('Solución gráfica')

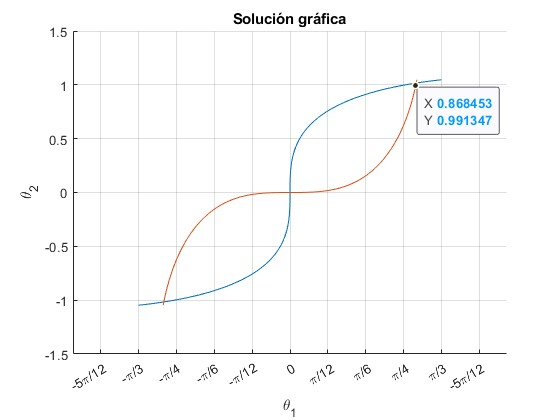
Utilizamos fsolve para obtener la solución numérica. Añadimos al script el código

...
F=@(x) [w2*(sin(x(1))+sin(x(2)))-tan(x(2)),  
w2*(2*sin(x(1))+sin(x(2)))-2*tan(x(1))];
th=fsolve(F,[pi/6,pi/3]);
disp(th)

El resultado es θ₁=0.8724 (50.0°), θ₂=1.0167 (58.2°) corresponde al primer modo

0.8724    1.0167

La solución gráfica para ω/ω_c=2 es

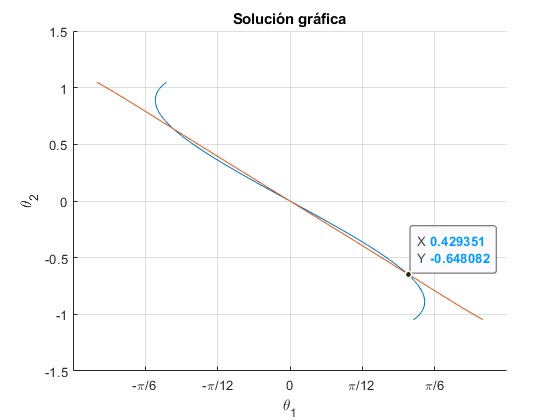
El resultado es θ₁=0.4226 (24.2°), θ₂=-0.6378 (-36.5°) corresponde al segundo modo

 0.4226    -0.6378

Aproximación

Si los ángulos de desviación son pequeños, aproximamos tanθ≈sinθ≈θ

${\displaystyle \begin{array}{l}\frac{{\theta }_2}{{\theta }_1+{\theta }_2}\approx \frac{2{\theta }_1}{2{\theta }_1+{\theta }_2}\\ {\theta }_2\approx \pm \sqrt{2}{\theta }_1\end{array}}$

Calculamos el cuadrado de la velocidad angular de rotación para cada una de las raíces

${\displaystyle \begin{array}{l}{\theta }_2\approx \sqrt{2}{\theta }_1\\ \frac{{\omega }^2}{{\omega }_c^2}\approx \frac{{\theta }_2}{{\theta }_1+{\theta }_2}=\frac{\sqrt{2}}{1+\sqrt{2}}=0.5858\\ {\theta }_2\approx -\sqrt{2}{\theta }_1\\ \frac{{\omega }^2}{{\omega }_c^2}\approx \frac{-\sqrt{2}}{1-\sqrt{2}}=\text{3}\text{.4142}\end{array}}$

El punto de sujección O dista d del eje de rotación

Las ecuaciones de equilibrio son similares, solamente cambia, r₁=d+lsinθ₁ y r₂=d+lsinθ₁+lsinθ₂, tal como se aprecia en la figura

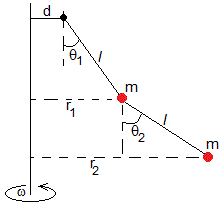
• Equilibrio de la segunda partícula

${\displaystyle \begin{array}{l}\{\begin{array}{l}{T}_2\sin {\theta }_2=m{\omega }^2{r}_2\\ T_2\cos {\theta }_2=mg\end{array}\\ \tan {\theta }_2=\frac{{\omega }^2{r}_2}{g}\\ {\omega }^2=\frac{g\tan {\theta }_2}{l\sin {\theta }_1+l\sin {\theta }_2+d}\\ \frac{{\omega }^2}{{\omega }_c^2}=\frac{\tan {\theta }_2}{\sin {\theta }_1+\sin {\theta }_2+\frac{d}{l}}\end{array}}$

• Equilibrio de la primera partícula

${\displaystyle \begin{array}{l}\{\begin{array}{l}{T}_1\sin {\theta }_1=m{\omega }^2{r}_1+T_2\sin {\theta }_2\\ T_1\cos {\theta }_1=mg+T_2\cos {\theta }_2\end{array}\\ \tan {\theta }_1=\frac{{\omega }^2\left(r_1+r_2\right)}{2g}\\ {\omega }^2=\frac{2g\tan {\theta }_1}{2l\sin {\theta }_1+l\sin {\theta }_2+2d}\\ \frac{{\omega }^2}{{\omega }_c^2}=\frac{2\tan {\theta }_1}{2\sin {\theta }_1+\sin {\theta }_2+2\frac{d}{l}}\end{array}}$

Dado θ₂ calculamos θ₁ resolviendo la ecuación trascendente

${\displaystyle \frac{\tan {\theta }_2}{\sin {\theta }_1+\sin {\theta }_2+\frac{d}{l}}=\frac{2\tan {\theta }_1}{2\sin {\theta }_1+\sin {\theta }_2+2\frac{d}{l}}}$

Representamos la función

${\displaystyle f\left({\theta }_1\right)=\tan {\theta }_2\left(2\sin {\theta }_1+\sin {\theta }_2+2\frac{d}{l}\right)-2\tan {\theta }_1\left(\sin {\theta }_1+\sin {\theta }_2+\frac{d}{l}\right)}$

l=0.2; %longitud del péndulo
d=0.02; %distancia al eje
th_2=15*pi/180;    
f=@(x) tan(th_2)*(2*sin(x)+sin(th_2)+2*d/l)-2*tan(x).*(d/l+sin(x)+sin(th_2));
fplot(f,[-pi/3,pi/3])
grid on
xlabel('\theta_1')
ylabel('f(\theta_1)')
title('Raíces')

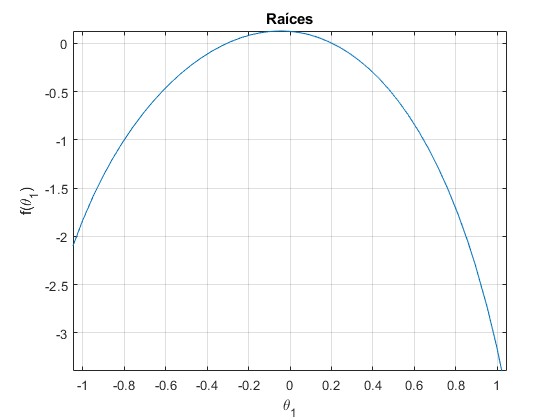
La ecuación trascendente f(θ₁)=0 tiene dos raíces una positiva y otra negativa. Para el ángulo θ₂=-12° la función es tangente al eje X. Para los ángulos -12° a 0° no corta al eje X, no hay raíces

Dado el ángulo θ₂ calculamos θ₁, utilizando la función punto_medio y con ambos ángulos, calculamos la velocidad angular de rotación ω/ω_c. Representamos la velocidad angular ω/ω_c en función del ángulo θ₂

function pendulo_rotacion_6   
    l=0.2; %longitud del péndulo
    d=0.02; %distancia al eje
    hold on
    ang_2=(1:80)*pi/180;
    w=zeros(1,length(ang_2));
    i=1;
    for th_2=ang_2 %th_2>0
        f=@(x) tan(th_2)*(2*sin(x)+sin(th_2)+2*d/l)-2*tan(x)*(d/l+sin(x)+
sin(th_2));
        th_1=punto_medio(f,0, pi/2);
        w(i)=sqrt(tan(th_2)/(d/l+sin(th_1)+sin(th_2)));
        i=i+1;
    end
    plot(ang_2,w)
    i=1;
    for th_2=ang_2 %th_2>0
        f=@(x) tan(th_2)*(2*sin(x)+sin(th_2)+2*d/l)-2*tan(x)*(d/l+sin(x)+
sin(th_2));
        th_1=punto_medio(f,0, -pi/2);
        w(i)=sqrt(tan(th_2)/(d/l+sin(th_1)+sin(th_2)));
        i=i+1;
    end
    plot(ang_2,w)
    
    ang_2=-(12:80)*pi/180; %th_2<0
    w=zeros(1,length(ang_2));
    i=1;
    for th_2=ang_2
        f=@(x) tan(th_2)*(2*sin(x)+sin(th_2)+2*d/l)-2*tan(x)*(d/l+sin(x)+
sin(th_2));
        th_1=punto_medio(f,0, -pi/2);
        w(i)=sqrt(tan(th_2)/(d/l+sin(th_1)+sin(th_2)));
        i=i+1;
    end
    plot(ang_2,w)
    i=1;
    for th_2=ang_2
        f=@(x) tan(th_2)*(2*sin(x)+sin(th_2)+2*d/l)-2*tan(x)*(d/l+sin(x)+
sin(th_2));
        th_1=punto_medio(f,0, pi/2);
        w(i)=sqrt(tan(th_2)/(d/l+sin(th_1)+sin(th_2)));
        i=i+1;
    end
    plot(ang_2,w)
    
    hold off
    set(gca,'XTick',-5*pi/12:pi/12:5*pi/12)
    set(gca,'XTickLabel',{'-5\pi/12','-\pi/3','-\pi/4','-\pi/6', '-\pi/12', 
'0','\pi/12','\pi/6','\pi/4','\pi/3','-5\pi/12'})
    grid on
    ylim([0,4])
    ylabel('\omega/\omega_c')
    xlabel('\theta_2')
    title('Péndulo cónico doble')

    function m=punto_medio(f, a, b)
        CERO=1e-10;
        ERROR=0.001;
        MAXITER=100;
        for k=1:MAXITER
            m=(a+b)/2;
            ym=f(m);
             if abs(ym)<CERO           
                break
             elseif abs((a-b)/m)<ERROR     
                break
             elseif (f(a)*ym)<0     
                b=m;
             else
                a=m;
             end
        end
        if(i==MAXITER) 
            error('no se ha encontrado la raiz')
        end
    end
end

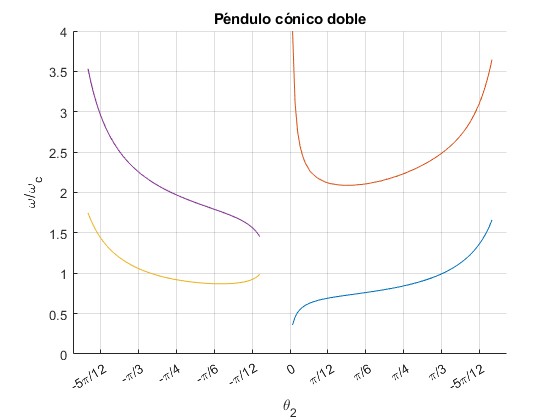
Para cada ángulo θ₂ hay dos posibles velocidades angulares ω/ω_c de rotación

Aproximación

Si los ángulos de desviación son pequeños, aproximamos tanθ≈sinθ≈θ

${\displaystyle \begin{array}{l}\frac{{\theta }_2}{{\theta }_1+{\theta }_2+\frac{d}{l}}\approx \frac{2{\theta }_1}{2{\theta }_1+{\theta }_2+2\frac{d}{l}}\\ {\theta }_1=\frac{1}{2}\left(-\frac{d}{l}\pm \sqrt{\frac{d^2}{l^2}+2{\theta }_2\frac{d}{l}+{\theta }_2^2}\right)\\ {\theta }_1=\{\begin{array}{l}\frac{{\theta }_2}{2}\\ -\frac{1}{2}\left(2\frac{d}{l}+{\theta }_2\right)\end{array}\end{array}}$

Péndulo cónico triple

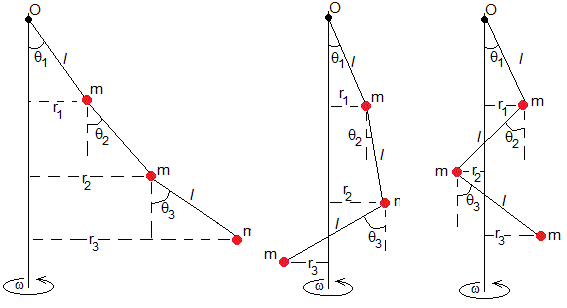
Un péndulo cónico triple, consta de una varilla rígida de longitud l y de masa despreciable sujeta por uno de sus extremos al eje de rotación, se fija al otro extremo una partícula de masa m. En esta partícula se fija el extremo del segundo péndulo cónico de las mismas dimensiones. En la segunda partícula se fija el extremos del tercer péndulo cónico de las mismas dimensiones

En la figura, se muestra los tres modos de rotación.

• Primer modo, θ₃>0
• Segundo modo, θ₃<0
• Tercer modo, θ₂<0

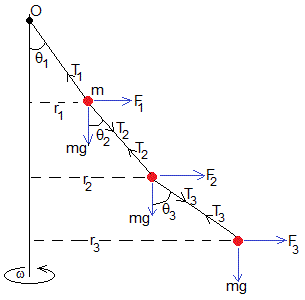
En la figura, se muestran las fuerzas sobre cada una de las dos partículas, T₁, T₂ y T₃ son las tensiones de las varillas y F₁=mω²r₁, F₂=mω²r₂ y F₃=mω²r₃ las fuerzas centrífugas.

• Equilibrio de la tercera partícula

${\displaystyle \begin{array}{l}\{\begin{array}{l}{T}_3\sin {\theta }_3=m{\omega }^2{r}_3\\ T_3\cos {\theta }_3=mg\end{array}\\ \tan {\theta }_3=\frac{{\omega }^2{r}_3}{g}\\ {\omega }^2=\frac{g\tan {\theta }_3}{l\sin {\theta }_1+l\sin {\theta }_2+l\sin {\theta }_3}\\ \frac{{\omega }^2}{{\omega }_c^2}=\frac{\tan {\theta }_3}{\sin {\theta }_1+\sin {\theta }_2+\sin {\theta }_3}\end{array}}$

• Equilibrio de la segunda partícula

${\displaystyle \begin{array}{l}\{\begin{array}{l}{T}_2\sin {\theta }_2=m{\omega }^2{r}_2+T_3\sin {\theta }_3\\ T_2\cos {\theta }_2=mg+T_3\cos {\theta }_3\end{array}\\ \tan {\theta }_2=\frac{{\omega }^2\left(r_2+r_3\right)}{2g}\\ \frac{{\omega }^2}{{\omega }_c^2}=\frac{2\tan {\theta }_2}{2\sin {\theta }_1+2\sin {\theta }_2+\sin {\theta }_3}\end{array}}$

• Equilibrio de la primera partícula

${\displaystyle \begin{array}{l}\{\begin{array}{l}{T}_1\sin {\theta }_2=m{\omega }^2{r}_1+T_2\sin {\theta }_2\\ T_1\cos {\theta }_1=mg+T_2\cos {\theta }_2\end{array}\\ \tan {\theta }_1=\frac{{\omega }^2\left(r_1+r_2+r_3\right)}{3g}\\ \frac{{\omega }^2}{{\omega }_c^2}=\frac{3\tan {\theta }_1}{3\sin {\theta }_1+2\sin {\theta }_2+\sin {\theta }_3}\end{array}}$

Dado θ₃, calculamos θ₂ y θ₁, resolviendo el sistema de dos ecuaciones trascendentes

${\displaystyle \frac{{\omega }^2}{{\omega }_c^2}=\frac{\tan {\theta }_3}{\sin {\theta }_1+\sin {\theta }_2+\sin {\theta }_3}=\frac{2\tan {\theta }_2}{2\sin {\theta }_1+2\sin {\theta }_2+\sin {\theta }_3}=\frac{3\tan {\theta }_1}{3\sin {\theta }_1+2\sin {\theta }_2+\sin {\theta }_3}}$

Aproximación

Si los ángulos de desviación son pequeños, aproximamos tanθ≈sinθ≈θ

${\displaystyle \frac{{\omega }^2}{{\omega }_c^2}\approx \frac{{\theta }_3}{{\theta }_1+{\theta }_2+{\theta }_3}\approx \frac{2{\theta }_2}{2{\theta }_1+2{\theta }_2+{\theta }_3}\approx \frac{3{\theta }_1}{3{\theta }_1+2{\theta }_2+{\theta }_3}}$

Llamamos x=θ₂/θ₁, y=θ₃/θ₁. Tenemos que resolver el sistema de dos ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{y}{1+x+y}=\frac{2x}{2+2x+y},\\ \frac{y}{1+x+y}=\frac{3}{3+2x+y}\end{array}\\ \{\begin{array}{l}2y+y^2=2x+2x^2\\ y^2+2xy=3+3x\end{array}\\ y=\frac{2x^2-x-3}{2\left(1-x\right)}\\ 2\left(\frac{2x^2-x-3}{2\left(1-x\right)}\right)+{\left(\frac{2x^2-x-3}{2\left(1-x\right)}\right)}^2=2x+2x^2\\ 4x^4+4x^3-9x^2-6x+3=0\end{array}}$

Una raíz es x=-1.

${\displaystyle 4x^4+4x^3-9x^2-6x+3=\left(x+1\right)\left(4x^3-9x+3\right)}$

Buscamos las tres raíces de la ecuación, 4x³-9x+3=0, con la función roots de MATLAB, o con la función raices_3

x=roots([4,0,-9,3]);
y=(2*x.^2-x-3)./(2*(1-x));
frec=sqrt(y./(1+x+y));
disp([x,y,frec])

   -1.6450    0.7669    2.5080
    1.2921    1.6312    0.6448
    0.3529   -2.3981    1.5147

El estudio de tres o más péndulos se complica debido a que las ecuaciones que tenemos que resolver son no lineales

Referencias

Rod Cross. A conical pendulum model of a rotating chain. Eur. J. Phys. 42 (2021) 035007

Rod Cross. Rotational modes of a double conical pendulum. Eur. J. Phys. 44 (2023) 025004