Partícula unida a un muelle no ideal
El movimiento armónico simple describe una gran variedad de situaciones físicas. En general, la energía potencial Ep(x) se puede desarrollar en serie alrededor de su posición de equilibrio estable, que tomaremos como x=0.
El término constante Ep(0) puede eliminarse ya que la energía potencial está definida salvo una constante aditiva.
El segundo término es cero, ya que en la posición de equilibrio x=0, la energía potencial presenta un mínimo y como consecuencia, el tercer término tiene que ser positivo.
El desarrollo en serie de la energía potencial Ep(x) es
Un oscilador es lineal (armónico simple) si todos los coeficientes a partir del tercero son nulos, por lo que expresamos la energía potencial en la forma
-
En un gran número de situaciones físicas, la amplitud de las oscilaciones es lo suficientemente pequeña de modo, que el término cuadrático es el único relevante.
-
Hay otros casos, en los que la energía potencial Ep(x) no se puede desarrollar en serie alrededor de la posición de equilibrio estable.
-
En otros, la energía potencial Ep(x) se puede desarrollar en serie alrededor de la posición de equilibrio estable, pero el término cuadrático es nulo y la serie comienza con un término superior al de segundo orden. En el ejemplo de esta página, vamos a incluir el término en x3 y observar los efectos.
Vamos a estudiar el movimiento de una partícula a lo largo del eje X cuando su energía potencial está definida por la función
Donde s se denomina constante de anarmonicidad. Cuando s=0, tenemos el conocido potencial simétrico de una partícula unida a un muelle ideal de constante k.
Energía
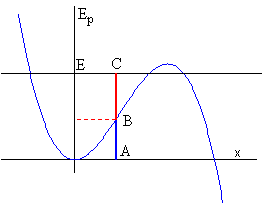
La energía total de la partícula en una posición x es la suma de la energía cinética y potencial
E=Ek+Ep(x)
En la figura el segmento AC representa la energía total E, el segmento AB la energía potencial y el BC la energía cinética.
Como la energía cinética no puede ser negativa, las abscisas de los dos puntos de intersección entre la recta horizontal (color negro) que señala la energía total constante E con la función Ep(x) (en color azul) marca los límites del movimiento de la partícula. Las abscisas de estos puntos son dos de las raíces de la ecuación cúbica
k=0.8; %constante del muelle
s=0.2; %anarmonicidad
energia=3; %energía
f=@(x) k*x.^2/2-s*k*x.^3/3;
fplot(f,[-5,10])
ylim([0,7])
line([-5,10],[energia,energia])
p=roots([-s*k/3,k/2,0,-energia]);
line([p(2),p(2)],[0,energia],'lineStyle','--')
line([p(3),p(3)],[0,energia],'lineStyle','--')
xlabel('x')
ylabel('E_p(x)')
title('Energía potencial')
grid on
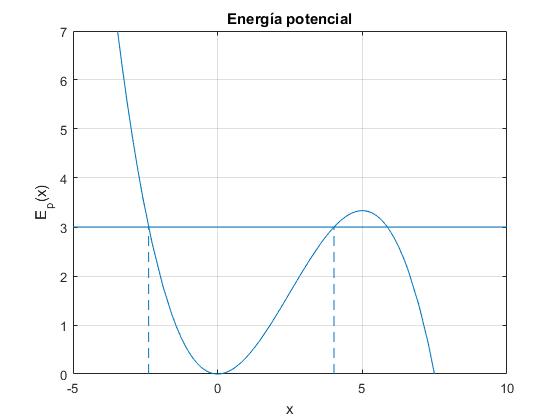
La energía potencial de la partícula es máxima en los dos puntos más alejados del origen, y es mínima en x=0, (posición de equilibrio). Lo contrario le ocurre a la energía cinética que es mínima (cero) en los dos puntos más alejados del origen y es máxima en el origen.
Fuerza
La fuerza sobre la partícula debida al muelle no ideal será
A la izquierda del origen x<0, la pendiente de la función Ep es negativa, la fuerza es positiva (hacia la derecha). A la derecha del origen x>0 la pendiente de la curva es positiva, la fuerza es negativa (hacia la izquierda).
Las posiciones de equilibrio en las que F=0 son x=0, y x=1/s la función Ep(x) presenta un mínimo y un máximo respectivamente.
La derivada segunda de la función energía potencial es
- Cuando x=0, la derivada segunda es positiva, tenemos un mínimo en la función energía potencial Ep(x) o posición de equilibrio estable.
- Cuando x=1/s, la derivada segunda es negativa, tenemos un máximo relativo en la función energía potencial Ep(x) o posición de equilibrio inestable. El valor del máximo es
Vamos a estudiar las oscilaciones de una partícula unida a un muelle no ideal en torno a la posición de equilibrio estable x=0.
Ecuación del movimiento
La ecuación del movimiento es
ma=-kx+skx2
o en forma de ecuación diferencial
ω0 es la frecuencia angular propia de una partícula de masa m unida al muelle ideal de constante k.
Se resuelve la ecuación diferencial por procedimiento numéricos, con las siguientes condiciones iniciales. En el instante t=0, la posición inicial de la partícula es x0 (a la derecha del origen) y su velocidad inicial es v0=0.
En la posición inicial, la energía cinética de la partícula es cero y por tanto, la energía potencial es igual a la energía total. Dada la energía total E de la partícula, hallamos la posición inicial x0. Para ello, hay que resolver la ecuación cúbica.
Si el valor de E es menor que el máximo, la raíz de la ecuación cúbica se encuentra en el intervalo comprendido entre x=0 y x=1/s.
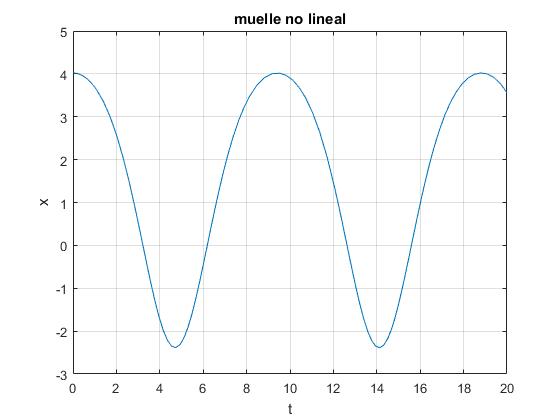
m=1; %masa
k=0.8; %constante del muelle
s=0.2; %anarmonicidad
energia=3; %energía
p=roots([-s*k/3,k/2,0,-energia])
x0=[p(2),0]; %segunda raíz
f=@(t,x) [x(2);-k*x(1)/m+s*k*x(1)^2/m];
[t,x]=ode45(f,[0,20],x0);
plot(t,x(:,1))
xlabel('t')
ylabel('x');
title('muelle no lineal')
grid on
Actividades
En el programa interactivo, se introducen los dos parámetros que describen el sistema formado por una partícula unida a un muelle no ideal.
- La constante elástica k del muelle en el control titulado Constante.
- La constante de anarmonicidad s, en el control titulado Anarmonicidad.
- La energía total E de la partícula en el control titulado Energía.
- La masa de la partícula se ha fijado en la unidad m=1.
Se pulsa el botón titulado Nuevo
Se representa la función energía potencial Ep(x) en la parte derecha.
Cambiando los valores de la constante elástica k y de la constante de anarmonicidad s, obtenemos diversas formas de la curva de energía potencial.
Si la energía E es mayor que la máxima (para x=1/s) el programa no prosigue, un mensaje nos avisa de que tenemos que introducir un valor menor de la energía.
En la ventana se puede observar tres zonas:
- A la derecha, la representación de la función energía potencial Ep(x). Los valores de la energía cinética y potencial de la partícula representados por barras de color rojo y azul.
- En la parte inferior izquierda, el movimiento de la partícula unida a un muelle elástico no ideal. Se representa mediante una flecha la fuerza sobre la partícula.
- En la parte superior izquierda, se representa la trayectoria de la partícula en el espacio de las fases.

