Movimiento de un pistón
El sistema biela-manivela de una máquina motriz (máquina de vapor, motor térmico) se compone de una biela AB cuyo extremo A llamado pie de biela, se desplaza a lo largo de una recta, mientras que el otro extremo B, llamado cabeza de biela, articulado en B con una manivela OB describe una circunferencia de radio OB. El pie de biela está articulado en una pieza denominada patín solidaria con el pistón que se desplaza entre dos guías.
Supongamos que la manivela tiene radio r y la biela tiene una longitud l (l>2r). La manivela gira con velocidad angular constante ω y el pistón oscila. La posición del pistón respecto del centro de la rueda es
Si situamos el origen en la posición en la posición del pistón para θ=90º.
Posición
Si la manivela se mueve con velocidad angular ω constante, la posición del pistón en función del tiempo es
-
El valor máximo se obtiene para ωt=0, y vale
-
El valor mínimo se obtiene para ωt=π,
En la figura, se representa la posición x del pistón en función del tiempo (color azul) y el MAS (color rojo)
x=r·sin(ω·t+π/2)=r·cos(ω·t)
-
El valor máximo se obtiene para ωt=0, y vale x=+r
- El valor mínimo se obtiene para ωt=π, y vale x=-r
syms w t l r;
%posición
x=r*cos(w*t)+sqrt(l^2-(r*sin(w*t))^2)-sqrt(l^2-r^2);
xx=subs(x,{w l r},{1 2 1}) %w=1, l=2, r=1
figure
hold on
ezplot(xx,[0 2*pi])
xp=cos(t); %Movimiento Armónico Simple de frecuencia angular w=1
h=ezplot(xp,[0 2*pi]);
set(h,'color','r')
ylim([-1.5 1.5])
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
title('posición')
xlabel('t')
ylabel('x')
grid on
hold off
xx =cos(t) - 3^(1/2) + (4 - sin(t)^2)^(1/2)
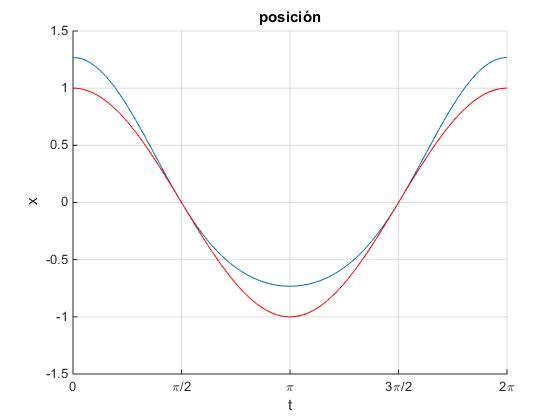
El movimiento del pistón no es armónico simple
Derivando la posición x con respecto al tiempo obtenemos la velocidad
En la figura, se representa la velocidad v del pistón en función del tiempo (color azul) y el MAS (color rojo)
v=-r·ω·sin(ω·t)
%velocidad
v=diff(x,t)
vv=subs(v,{w l r},{1 2 1}) %w=1, l=2, r=1
figure
hold on
ezplot(vv,[0 2*pi])
vp=-sin(t); %Movimiento Armónico Simple de frecuencia angular w=1
h=ezplot(vp,[0 2*pi]);
set(h,'color','r')
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
title('velocidad')
xlabel('t')
ylabel('v')
grid on
hold off
v =- r*w*sin(t*w) - (r^2*w*cos(t*w)*sin(t*w))/(l^2 - r^2*sin(t*w)^2)^(1/2) vv =- sin(t) - (cos(t)*sin(t))/(4 - sin(t)^2)^(1/2)
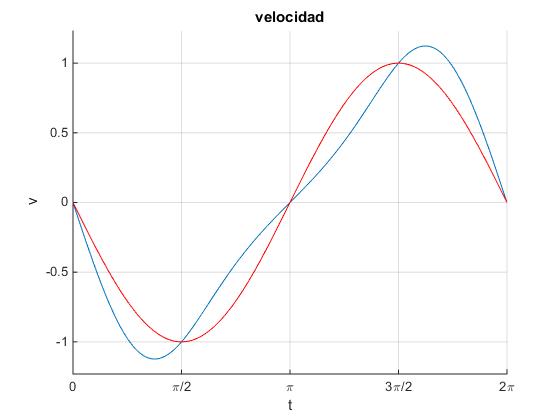
Aceleración
Derivando la velocidad v con respecto al tiempo obtenemos la aceleración
En la figura, se representa la aceleración a del pistón en función del tiempo (color azul) y el MAS (color rojo)
a=-r·ω2·cos(ω·t)
%aceleración
a=diff(v,t);
a=simplify(a)
aa=subs(a,{w l r},{1 2 1}) %w=1, l=2, r=1
figure
hold on
ezplot(aa,[0 2*pi])
ap=-cos(t); %Movimiento Armónico Simple de frecuencia angular w=1
h=ezplot(ap,[0 2*pi]);
set(h,'color','r')
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
title('aceleración')
ylim([-1.5 1.5])
xlabel('t')
ylabel('a')
grid on
hold off
a =-(r^4*w^2*sin(t*w)^4 + r*w^2*cos(t*w)*(l^2 -
r^2*sin(t*w)^2)^(3/2) +l^2*r^2*w^2*cos(t*w)^2 -
l^2*r^2*w^2*sin(t*w)^2)/(l^2 - r^2*sin(t*w)^2)^(3/2)
aa =-(4*cos(t)^2 - 4*sin(t)^2 + sin(t)^4 +
cos(t)*(4 - sin(t)^2)^(3/2))/(4 - sin(t)^2)^(3/2)
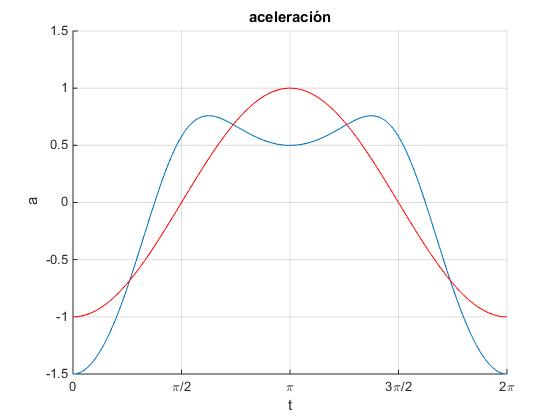
La aceleración en un Movimiento Armónico Simple difiere de la aceleración del pistón tal como vemos en la gráfica. El movimiento del pistón es oscilatorio pero no es Armónico Simple.
Aceleración nula, máxima velocidad
La velocidad es máxima cuando la aceleración es cero. Para calcular los ángulos ω·t para los cuales la aceleración es cero, hay que resolver la ecuación
Las operaciones que hay que realizar son las siguientes
Se sustituye sin2(ωt)=1-cos2(ωt) y cos(2ωt)= cos2(ωt) - sin2(ωt) =2 cos2(ωt)-1
Se eleva al cuadrado ambos miembros
y después de realizar algunas operaciones algebraicas se llega a la ecuación
Haciendo el cambio de variable z=cos2(ωt) se obtiene la ecuación cúbica
Conocida las raíces de la ecuación cúbica z se calcula el ángulo ωt.
De las tres raíces, una es negativa (no se puede hallar la raíz cuadrada), otra es mayor que la unidad (la raíz es también mayor que la unidad y no se puede calcular en arco coseno) y la tercera, la única válida, está comprendida entre 0 y 1.
La aceleración es nula en dos instantes
Ejemplo:
-
Sea r=1.0 y l=2.0
La ecuación cúbica tiene tres raíces reales
z1=-5.172
z2=4.028
z3=0.1434
La velocidad es máxima (en módulo) o la aceleración es cero para
>> z=solve(aa); >> double(z) ans = 1.5708 - 1.5600i -1.5708 + 1.5600i 1.1816 + 0.0000i -0.0000 - 1.3210i -1.1816 - 0.0000i 0.0000 + 1.3210i
Como vemos hay dos tiempos para los cuales la velocidad es máxima o la aceleración es nula: 1.1816 y 2π-1.1816=5.1016.
Representamos en el eje horizontal, el cociente r/l y en el eje vertical los instantes ωt para los cuales la velocidad es máxima. Calculamos las raíces de la ecuación cúbica, mediante la función raices_3 que se describe en la página titulada 'Raíces de una ecuación (I)', alternativamente, se puede utilizar la función roots de MATLAB
r_l=0.05:0.025:0.975;
t=zeros(1,length(c));
i=1;
for k=r_l
b=(1-3*k^2)/k^2;
c=-(1-k^2)*(1+3*k^2)/k^4;
d=(1-k^2)/k^2;
raices=raices_3([1,b,c,d]);
%raices=roots([1,b,c,d]);
r=min(raices(raices>0));
t(i)=acos(sqrt(r));
i=i+1;
end
plot(r_l,t);
grid on
xlabel('r/l')
ylabel('\omega·t')
title('Velocidad máxima')
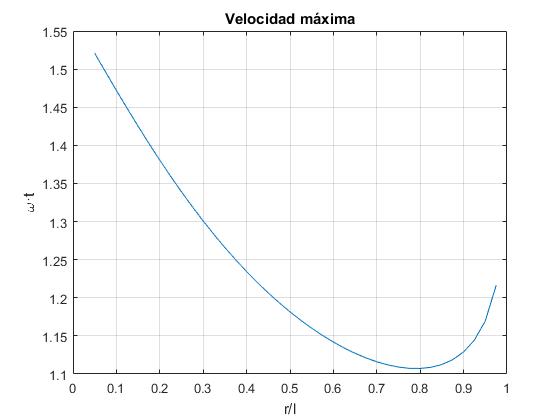
Referencias
Ralph Hoyt Bacon. The motion of a piston. Am. J. Phys. Vol. 10, (1942) pp. 145-147

