Sea una partícula de masa m unida a un hilo inextensible y de masa despreciable de longitud l cuyo extremo cuelga del centro de suspensión O.

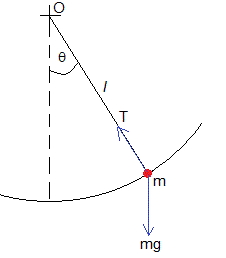
Cuando la partícula se desplaza un ángulo θ, las fuerzas que actúan sobre la partícula son:

• el peso, mg
• la tensión T de la cuerda

La velocidad en coordenadas polares es

${\displaystyle \overrightarrow{v}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }}$

La aceleración en coordenadas polares es

${\displaystyle \overrightarrow{a}=\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }}$

Siendo la distancia radial r la longitud l variable del péndulo. Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}m\left(\frac{d^{2}l}{d{t}^2}-l{\left(\frac{d\theta }{dt}\right)}^2\right)=-T+mg\cos \theta \\ m\left(l\frac{d^2\theta }{d{t}^2}+2\frac{dl}{dt}\frac{d\theta }{dt}\right)=-mg\sin \theta \end{array}}$

La segunda es la ecuación diferencial del movimiento

${\displaystyle l\frac{d^2\theta }{d{t}^2}+2\frac{dl}{dt}\frac{d\theta }{dt}+g\sin \theta =0}$

La longitud del péndulo aumenta linealmente con el tiempo

Si la longitud de la cuerda varía con el tiempo de la forma l=l₀+αt, la ecuación del movimiento se escribe, haciendo la sustitución

${\displaystyle \begin{array}{l}\frac{d\theta }{dt}=\frac{dl}{dt}\frac{d\theta }{dl}=\alpha \frac{d\theta }{dl}\\ \frac{d^2\theta }{d{t}^2}=\frac{d}{dt}\left(\frac{d\theta }{dt}\right)=\frac{d}{dl}\left(\alpha \frac{d\theta }{dl}\right)\frac{dl}{dt}={\alpha }^2\frac{d^2\theta }{d{l}^2}\end{array}}$

de la forma

${\displaystyle l\frac{d^2\theta }{d{l}^2}+2\frac{d\theta }{dl}+\frac{g}{{\alpha }^2}\sin \theta =0}$

Cuando la amplitud de la oscilación es pequeña, sinθ≈θ

${\displaystyle l\frac{d^2\theta }{d{l}^2}+2\frac{d\theta }{dl}+\frac{g}{{\alpha }^2}\theta =0}$

Se hace los cambios de variable

${\displaystyle \begin{array}{l}y=\theta ·x\\ x=\frac{2}{\alpha }\sqrt{gl}\\ \frac{dx}{dl}=\frac{1}{\alpha }\sqrt{\frac{g}{l}}=\frac{2g}{{\alpha }^2}\frac{1}{x}\end{array}}$

Haciendo operaciones

${\displaystyle \begin{array}{l}\frac{d\theta }{dl}=\frac{d\theta }{dx}·\frac{dx}{dl}=\frac{d}{dx}\left(\frac{y}{x}\right)·\frac{dx}{dl}=\frac{2g}{{\alpha }^2}\left(\frac{1}{x^2}\frac{dy}{dx}-\frac{y}{x^3}\right)\\ \frac{d^2\theta }{d{l}^2}=\frac{d}{dl}\left(\frac{d\theta }{dl}\right)=\frac{d}{dx}\left(\frac{d\theta }{dl}\right)\frac{dx}{dl}=\frac{4g^2}{{\alpha }^4}\frac{1}{x}\frac{d}{dx}\left(\frac{1}{x^2}\frac{dy}{dx}-\frac{y}{x^3}\right)=\frac{4g^2}{{\alpha }^4}\frac{1}{x}\frac{d}{dx}\left(-\frac{3}{x^3}\frac{dy}{dx}+\frac{1}{x^2}\frac{d^{2}y}{d{x}^2}+\frac{3}{x^4}y\right)\\ l\frac{d^2\theta }{d{l}^2}+2\frac{d\theta }{dl}+\frac{g}{{\alpha }^2}\theta =\frac{{\alpha }^2{x}^2}{4g}\frac{4g^2}{{\alpha }^4}\frac{1}{x}\left(-\frac{3}{x^3}\frac{dy}{dx}+\frac{1}{x^2}\frac{d^{2}y}{d{x}^2}+\frac{3}{x^4}y\right)+2\frac{2g}{{\alpha }^2}\left(\frac{1}{x^2}\frac{dy}{dx}-\frac{y}{x^3}\right)+\frac{g}{{\alpha }^2}\frac{1}{x}y=0\\ \frac{1}{x}\frac{d^{2}y}{d{x}^2}+\frac{1}{x^2}\frac{dy}{dx}-\frac{y}{x^3}+\frac{y}{x}=0\end{array}}$

Llegamos a la ecuación de Bessel con n=1

${\displaystyle \frac{d^{2}y}{d{x}^2}+x\frac{dy}{dx}+(x^2-1)y=0}$

La solución es

${\displaystyle \begin{array}{l}y=A{J}_1(x)+B{Y}_1(x)\\ \theta =\frac{1}{x}\left(A{J}_1\left(x\right)+B{Y}_1\left(x\right)\right)\\ \theta =\frac{\alpha }{2\sqrt{gl}}\left(A{J}_1\left(\frac{2}{\alpha }\sqrt{gl}\right)+B{Y}_1\left(\frac{2}{\alpha }\sqrt{gl}\right)\right)\end{array}}$

Derivamos respecto del tiempo, para obtener la velocidad angular dθ/dt

Utilizamos la relación entre las funciones de Bessel y sus derivadas

${\displaystyle \frac{d{J}_n(x)}{dx}=n\frac{J_n(x)}{x}-J_{n+1}(x)}$

Partimos de la expresión θ(x)

${\displaystyle \begin{array}{l}\frac{d}{dt}{J}_1\left(x\right)=\frac{d}{dx}{J}_1\left(x\right)\frac{dx}{dt}=\left(\frac{J_1(x)}{x}-J_2(x)\right)\frac{dx}{dt}\\ \frac{d\theta }{dt}=\frac{d\theta }{dx}\frac{dx}{dt}=\left\{-\frac{1}{x^2}\left(A{J}_1\left(x\right)+B{Y}_1\left(x\right)\right)+\frac{1}{x}\left\{A\left(\frac{J_1(x)}{x}-J_2(x)\right)+B\left(\frac{Y_1(x)}{x}-Y_2(x)\right)\right\}\right\}\frac{dx}{dt}\\ \frac{d\theta }{dt}=-\frac{1}{x}\left(A{J}_2(x)+B{Y}_2(x)\right)\frac{dx}{dt}\\ \frac{d\theta }{dt}=-\frac{\alpha }{2\sqrt{gl}}\left(A{J}_2\left(\frac{2}{\alpha }\sqrt{gl}\right)+B{Y}_2\left(\frac{2}{\alpha }\sqrt{gl}\right)\right)\frac{1}{\alpha }\sqrt{\frac{g}{l}}\alpha \end{array}}$

El resultado es

${\displaystyle \frac{d\theta }{dt}=-\frac{\alpha }{2l}\left(A{J}_2\left(\frac{2}{\alpha }\sqrt{gl}\right)+B{Y}_2\left(\frac{2}{\alpha }\sqrt{gl}\right)\right)}$

Las condiciones iniciales son: t=0, θ=θ₀, dθ/dt=0. En el instante inicial, cuando la longitud del péndulo es l₀, se desvía un ángulo θ₀ y se suelta. Calculamos los coeficientes A y B en el sistema de dos ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\theta }_0=\frac{\alpha }{2\sqrt{g{l}_0}}\left(A{J}_1\left(\frac{2}{\alpha }\sqrt{g{l}_0}\right)+B{Y}_1\left(\frac{2}{\alpha }\sqrt{g{l}_0}\right)\right)\\ 0=-\frac{\alpha }{2l_0}\left(A{J}_2\left(\frac{2}{\alpha }\sqrt{g{l}_0}\right)+B{Y}_2\left(\frac{2}{\alpha }\sqrt{g{l}_0}\right)\right)\end{array}\\ \theta ={\theta }_0\sqrt{\frac{l_0}{l}}\frac{J_2\left(\frac{2}{\alpha }\sqrt{g{l}_0}\right)Y_1\left(\frac{2}{\alpha }\sqrt{gl}\right)-Y_2\left(\frac{2}{\alpha }\sqrt{g{l}_0}\right)J_1\left(\frac{2}{\alpha }\sqrt{gl}\right)}{J_2\left(\frac{2}{\alpha }\sqrt{g{l}_0}\right)Y_1\left(\frac{2}{\alpha }\sqrt{g{l}_0}\right)-Y_2\left(\frac{2}{\alpha }\sqrt{g{l}_0}\right)J_1\left(\frac{2}{\alpha }\sqrt{g{l}_0}\right)}\end{array}}$

Comprobamos que en el instante t=0, l=l₀ y se cumple θ=θ₀

Teniendo en cuenta la relación

${\displaystyle J_2(x)Y_1(x)-J_1(x)Y_2(x)=\frac{2}{\pi x}}$

Llegamos a una expresión más simplificada

${\displaystyle \theta =\pi \sqrt{\frac{g}{l}}\frac{l_0}{\alpha }\left\{J_2\left(2\frac{\sqrt{g{l}_0}}{\alpha }\right)Y_1\left(2\frac{\sqrt{gl}}{\alpha }\right)-Y_2\left(2\frac{\sqrt{g{l}_0}}{\alpha }\right)J_1\left(2\frac{\sqrt{gl}}{\alpha }\right)\right\}{\theta }_0}$

Aproximaciones

Las funciones de Bessel se pueden aproximar a

${\displaystyle \begin{array}{l}{J}_n(x)\approx \sqrt{\frac{2}{\pi x}}\cos \left(x-n\frac{\pi }{2}-\frac{\pi }{4}\right)\\ Y_n(x)\approx \sqrt{\frac{2}{\pi x}}\sin \left(x-n\frac{\pi }{2}-\frac{\pi }{4}\right)\end{array}}$

Obtenemos una expresión más sencilla para la solución analítica

${\displaystyle \theta \approx {\left(\frac{l_0}{l}\right)}^{3/4}{\theta }_0\sin \left(2\frac{\sqrt{gl}}{\alpha }-2\frac{\sqrt{g{l}_0}}{\alpha }+\frac{\pi }{2}\right)={\left(\frac{l_0}{l}\right)}^{3/4}{\theta }_0\cos \left(2\frac{\sqrt{g{l}_0}}{\alpha }\left(\sqrt{\frac{l}{l_0}}-1\right)\right)}$

dado que l=l₀+αt, la amplitud (coeficiente del coseno) es una función decreciente del tiempo.

Sea la longitud inicial del péndulo l₀=1 m y α=0.1 m/s. Representamos la solución exacta y aproximada para una desviación inicial de θ₀=0.3 rad (17°). Observamos que no se aprecia diferencia entre ambas

alfa=0.1; %velocidad de incremento de la longitud
l0=1;   %longitud incial
th_0=0.3; %amplitud inicial

th=@(t) (pi*l0*sqrt(9.8./(l0+alfa*t))*th_0/alfa).*
(besselj(2,2*sqrt(9.8*l0)/alfa)*bessely(1,2*sqrt(9.8*(l0+alfa*t))/alfa)-
bessely(2,2*sqrt(9.8*l0)/alfa)*
besselj(1,2*sqrt(9.8*(l0+alfa*t))/alfa));

%aproximación
th_a=@(t) (l0./(l0+alfa*t)).^(3/4)*th_0.*cos(2*sqrt(9.8*l0)*(sqrt((l0+alfa*t)
/l0)-1)/alfa);
hold on
fplot(th,[0,50])
fplot(th_a,[0,50])
hold off
grid on
legend('exacta','aproximada')
xlabel('t')
ylabel('\theta')
title('Péndulo de longitud variable')

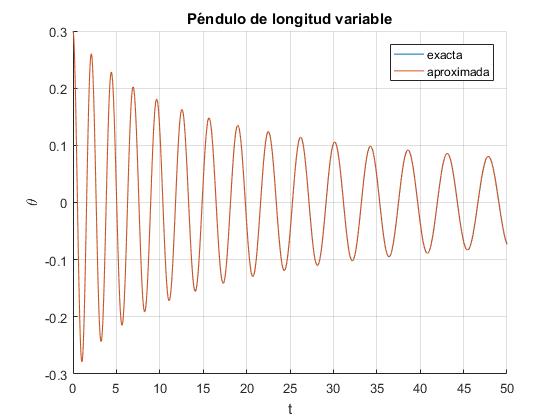
En este caso, la amplitud de la oscilación se va haciendo cada vez más pequeña

Periodo

Como vemos en la gráfica, el periodo tampoco es constante, aumenta con el tiempo

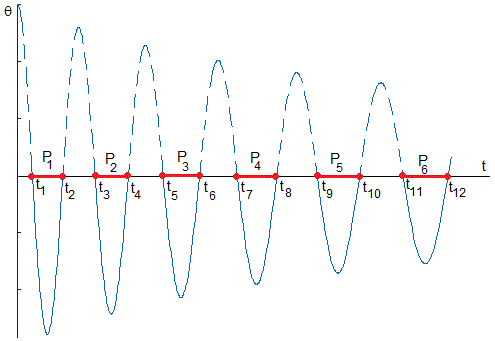
El péndulo pasa por la posición vertical de equilibrio cuando el coseno es cero, es decir cuando su argumento es π/2, 3π/2, 5π/2, etc.

${\displaystyle 2\frac{\sqrt{g{l}_0}}{\alpha }\left(\sqrt{\frac{l_0+\alpha t_n}{l_0}}-1\right)=\left(2n-1\right)\frac{\pi }{2}n=\mathrm{1,2,3...}}$

El instante t₁ en la figura se calcula cuando n=1, el instante t₂ cuando n=2, el instante t₃, cuando n=3 y así, sucesivamente.

${\displaystyle \sqrt{\frac{l_0+\alpha t_n}{l_0}}=\left(2n-1\right)\frac{\pi }{4}\frac{\alpha }{\sqrt{g{l}_0}}+1}$

Elevando al cuadrado, despejamos t_n

${\displaystyle l_0+\alpha t_n={\left(2n-1\right)}^2\frac{{\pi }^2}{16}\frac{{\alpha }^2}{g}+1+\left(2n-1\right)\frac{\pi }{2}\alpha \sqrt{\frac{l_0}{g}}}$

El tiempo que tarda el péndulo en pasar dos veces consecutivas por el origen es medio periodo, intervalo de tiempo marcado en color rojo en la figura. Así, P₁=t₂-t₁, P₂=t₄-t₃, P₃=t₆-t₅ y así, sucesivamente

${\displaystyle \begin{array}{l}{P}_n=t_{2n}-t_{2n-1}=\left\{{\left(4n-1\right)}^2-{\left(4n-3\right)}^2\right\}\frac{{\pi }^2}{16}\frac{\alpha }{g}+\left\{\left(4n-1\right)-\left(4n-3\right)\right\}\frac{\pi }{2}\sqrt{\frac{l_0}{g}}=\\ \left(2n-1\right)\frac{{\pi }^2}{2}\frac{\alpha }{g}+\pi \sqrt{\frac{l_0}{g}}\end{array}}$

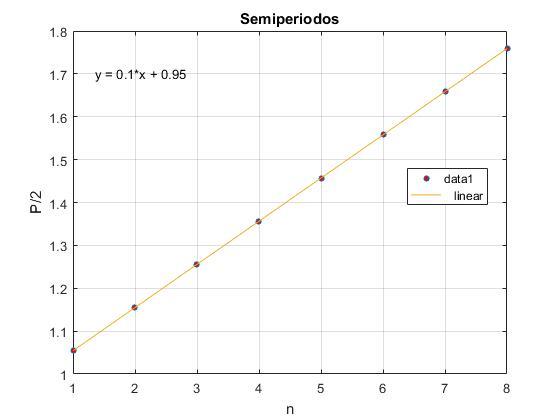
P_n es una función lineal de n, (el número de oscilación), de pendiente π²α/g

Procedimientos numéricos

Cuando la amplitud es grande, resolvemos la ecuación diferencial

${\displaystyle \frac{d^2\theta }{d{t}^2}+2\frac{\alpha }{l}\frac{d\theta }{dt}+\frac{g}{l}\sin \theta =0}$

por procedimientos numéricos, con las condiciones iniciales: t=0, θ=θ₀, dθ/dt=0. En el instante inicial, cuando la longitud del péndulo es l₀, se desvía un ángulo θ₀ y se suelta

alfa=0.1; %velocidad de incremento de la longitud
l0=1;   %longitud incial
th_0=pi/3;  %amplitud inicial

f=@(t,x) [x(2);-2*alfa*x(2)/(l0+alfa*t)-9.8*x(1)/(l0+alfa*t)]; 
opts=odeset('events',@pendulo_longitud_ode45);
[t,x,te,xe,ie]=ode45(f,[0,25],[th_0,0],opts);

hold on
plot(t,x(:,1),'r')
plot(te(ie==1),xe(ie==1),'o','markersize',4,'markerfacecolor','b')
hold off
grid on
xlabel('t')
ylabel('\theta');
title('Péndulo de longitud variable')

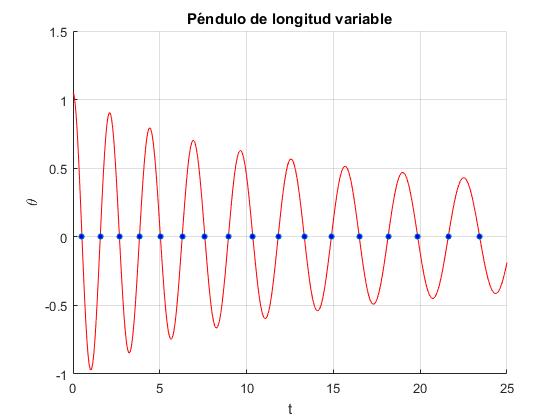
En la gráfica, marcamos los instantes t₁,t₂,t₃,... en los que el péndulo pasa por la posición vertical de equilibrio θ=0, para ello definimos la función pendulo_longitud_ode45 que pasamos al procedimiento ode45

function [detect,stopin,direction]=pendulo_longitud_ode45(~,x)
    detect=x(1); 
    stopin=0;
    direction=0; 
end

Completamos el script, representando los semiperiodos P_n=t_2n-t_2n-1 en el eje vertical y el número n de oscilación en el eje horizontal.

....
figure
N=floor(length(te)/2);
P=zeros(N,1);
for i=1:N
    P(i)=te(2*i)-te(2*i-1);
end
plot(1:N,P, 'o','markersize',4,'markerfacecolor','r');
grid on
xlabel('n')
ylabel('P/2')
title('Semiperiodos')

En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.

Observamos que los datos se ajustan a una línea recta de pendiente, 0.1. Con los datos α=0.1 y g=9.8, el valor de la pendiente es π²α/g=0.1

Energía

La energía en cualquier instante t (en coordenadas polares)

${\displaystyle E=\frac{1}{2}m\left({\left(\frac{dl}{dt}\right)}^2+l^2{\left(\frac{d\theta }{dt}\right)}^2\right)-mgl\cos \theta }$

Actividades

Se introduce

• El parámetro α en el contro titulado Parámetro
• El péndulo se desvía un ángulo inicial θ₀ en el control Angulo
• Se ha fijado la longitud inicial del péndulo l₀= 1 m

Se pulsa el botón titulado Nuevo

Observamos la trayectoria de la partícula a medida que se incrementa la longitud del péndulo. En la parte superior derecha se proporcionan los datos de:

• El tiempo t
• La longitud del péndulo, l en dicho instante
• El ángulo θ de desviación del péndulo en grados. Observamos como disminuye la amplitud
• La velocidad tangencial l·dθ/dt de la partícula en dicho instante

El movimiento se detiene cuando la longitud del péndulo alcanza el valor de l=3 m

La longitud del péndulo aumenta exponencialmente con el tiempo

Cuando la longitud del péndulo aumenta exponencialmente con el tiempo, l=l₀exp(αt), la ecuación diferencial, para pequeñas oscilaciones

${\displaystyle l\frac{d^2\theta }{d{t}^2}+2\frac{dl}{dt}\frac{d\theta }{dt}+g\theta =0}$

admite una solución analítica en términos de las funciones de Bessel, como en el caso anterior

La ecuación diferencial se convierte en

${\displaystyle \frac{d^2\theta }{d{t}^2}+2\alpha \frac{d\theta }{dt}+\frac{g}{l_0}{e}^{-\alpha t}\theta =0}$

Se hace el cambio de variable, τ=α·t

${\displaystyle \begin{array}{l}{\alpha }^2\frac{d^2\theta }{d{\tau }^2}+2{\alpha }^2\frac{d\theta }{d\tau }+\frac{g}{l_0}{e}^{-\tau }\theta =0\\ \frac{d^2\theta }{d{\tau }^2}+2\frac{d\theta }{d\tau }+{\omega }_0^2{e}^{-\tau }\theta =\mathrm{0,}{\omega }_0^2=\frac{1}{{\alpha }^2}\frac{g}{l_0}\end{array}}$

Se hace un nuevo cambio de variable

${\displaystyle \begin{array}{l}\theta =y{e}^{-\tau }\\ \frac{d\theta }{d\tau }=e^{-\tau }\frac{dy}{d\tau }-e^{-\tau }y\\ \frac{d^2\theta }{d{\tau }^2}=-2e^{-\tau }\frac{dy}{d\tau }+e^{-\tau }\frac{d^{2}y}{d{\tau }^2}+e^{-\tau }y\end{array}}$

La ecuación diferencial se transforma en

${\displaystyle \frac{d^{2}y}{d{\tau }^2}+\left({\omega }_0^2{e}^{-\tau }-1\right)y=0}$

Finalmente, hacemos el cambio de variable

${\displaystyle \begin{array}{l}x=2{\omega }_0{e}^{-\tau /2}\\ \frac{dy}{d\tau }=\frac{dy}{dx}\frac{dx}{d\tau }=-{\omega }_0{e}^{-\tau /2}\frac{dy}{dx}=-\frac{x}{2}\frac{dy}{dx}\\ \frac{d^{2}y}{d{\tau }^2}=\frac{d}{dx}\left(\frac{dy}{d\tau }\right)\frac{dx}{d\tau }=\frac{d}{dx}\left(-\frac{x}{2}\frac{dy}{dx}\right)\left(-{\omega }_0{e}^{-\tau /2}\right)=\frac{x}{4}\frac{dy}{dx}+\frac{x^2}{4}\frac{d^{2}y}{d{x}^2}\end{array}}$

La ecuación diferencial se transforma en

${\displaystyle x^2\frac{d^{2}y}{d{x}^2}+x\frac{dy}{dx}+\left(x^2-2^2\right)y=0}$

Llegamos a la ecuación de Bessel con n=2. La solución es

${\displaystyle \begin{array}{l}y=A{J}_2(x)+B{Y}_2(x)\\ \theta =e^{-\tau }\left(A{J}_2(x)+B{Y}_2(x)\right),x=2{\omega }_0{e}^{-\tau /2}\end{array}}$

Derivamos respecto del tiempo, para obtener la velocidad angular dθ/dt

${\displaystyle \begin{array}{l}\theta =\frac{x^2}{4{\omega }_0^2}\left(A{J}_2(x)+B{Y}_2(x)\right)=\frac{1}{4{\omega }_0^2}\left(A{x}^2{J}_2(x)+B{x}^2{Y}_2(x)\right)\\ \frac{d\theta }{d\tau }=\frac{d\theta }{dx}\frac{dx}{d\tau }=\frac{1}{4{\omega }_0^2}\left\{A\frac{d}{dx}\left(x^2{J}_2(x)\right)+B\frac{d}{dx}\left(x^2{Y}_2(x)\right)\right\}\left(-{\omega }_0{e}^{-\tau /2}\right)=\\ -\frac{x}{8{\omega }_0^2}\left(A{x}^2{J}_1(x)+B{x}^2{Y}_1(x)\right)=-\frac{x^3}{8{\omega }_0^2}\left(A{J}_1(x)+B{Y}_1(x)\right)\end{array}}$

Hemos utilizado las propiedades de las funciones de Bessel

${\displaystyle \frac{d}{dx}\left(x^2{J}_2(x)\right)=x^2{J}_1(x),\frac{d}{dx}\left(x^2{Y}_2(x)\right)=x^2{Y}_1(x)}$

>> syms x;
>> z=diff(besselj(2,x)*x^2)
>> simplify(z)
z =x^2*besselj(1, x)
>> z=diff(bessely(2,x)*x^2);
>> simplify(z)
z=x^2*bessely(1, x)

La posicicón θ y la velocidad angular en función del tiempo τ se expresan

${\displaystyle \begin{array}{l}\theta =e^{-\tau }\left(A{J}_2\left(2{\omega }_0{e}^{-\tau /2}\right)+B{Y}_2\left(2{\omega }_0{e}^{-\tau /2}\right)\right)\\ \frac{d\theta }{d\tau }=-{\omega }_0{e}^{-3\tau /2}\left(A{J}_1\left(2{\omega }_0{e}^{-\tau /2}\right)+B{Y}_1\left(2{\omega }_0{e}^{-\tau /2}\right)\right)\end{array}}$

Las condiciones iniciales son: t=0, θ=θ₀, dθ/dt=0. En el instante inicial, cuando la longitud del péndulo es l₀, se desvía un ángulo θ₀ y se suelta. Calculamos los coeficientes A y B en el sistema de dos ecuaciones

${\displaystyle \{\begin{array}{l}{\theta }_0=A{J}_2(2{\omega }_0)+B{Y}_2(2{\omega }_0)\\ 0=A{J}_1(2{\omega }_0)+B{Y}_1(2{\omega }_0)\end{array}}$

El resultado es

${\displaystyle \theta ={\theta }_0{e}^{-\tau }\frac{Y_1\left(2{\omega }_0\right)J_2\left(2{\omega }_0{e}^{-\tau /2}\right)-J_1\left(2{\omega }_0\right)Y_2\left(2{\omega }_0{e}^{-\tau /2}\right)}{Y_1\left(2{\omega }_0\right)J_2\left(2{\omega }_0\right)-J_1\left(2{\omega }_0\right)Y_2\left(2{\omega }_0\right)}}$

Teniendo en cuenta la relación

${\displaystyle J_2(x)Y_1(x)-J_1(x)Y_2(x)=\frac{2}{\pi x}}$

La expresión final en función del tiempo t

${\displaystyle \theta ={\theta }_0\pi {\omega }_0{e}^{-\alpha t}\left(Y_1\left(2{\omega }_0\right)J_2\left(2{\omega }_0{e}^{-\alpha t/2}\right)-J_1\left(2{\omega }_0\right)Y_2\left(2{\omega }_0{e}^{-\alpha t/2}\right)\right)}$

Aproximaciones

Las funciones de Bessel se pueden aproximar a

${\displaystyle \begin{array}{l}{J}_n(x)\approx \sqrt{\frac{2}{\pi x}}\cos \left(x-n\frac{\pi }{2}-\frac{\pi }{4}\right)\\ Y_n(x)\approx \sqrt{\frac{2}{\pi x}}\sin \left(x-n\frac{\pi }{2}-\frac{\pi }{4}\right)\end{array}}$

Obtenemos una expresión más sencilla para la solución analítica

${\displaystyle \begin{array}{l}\theta \approx {\theta }_0\pi {\omega }_0{e}^{-\alpha t}\left\{\frac{e^{-\alpha t/4}}{\pi {\omega }_0}\left(\sin \left(2{\omega }_0-\frac{3\pi }{4}\right)\cos \left(2{\omega }_0{e}^{-\alpha t/2}-\frac{5\pi }{4}\right)-\cos \left(2{\omega }_0-\frac{3\pi }{4}\right)\sin \left(2{\omega }_0{e}^{-\alpha t/2}-\frac{5\pi }{4}\right)\right)\right\}=\\ {\theta }_0{e}^{-3\alpha t/4}\sin \left(2{\omega }_0-\frac{3\pi }{4}-2{\omega }_0{e}^{-\alpha t/2}+\frac{5\pi }{4}\right)={\theta }_0{e}^{-3\alpha t/4}\cos \left(2{\omega }_0\left(1-e^{-\alpha t/2}\right)\right)\end{array}}$

Sea la longitud inicial del péndulo l₀=1 m y α=0.1 m/s. Representamos la solución exacta y aproximada para una desviación inicial de θ₀=0.3 rad (17°). Observamos que no se aprecia diferencia entre ambas

alfa=0.1; %velocidad de incremento de la longitud
l0=1;   %longitud incial
w0=sqrt(9.8/l0)/alfa;
th_0=0.3; %amplitud inicial
 
th=@(t) th_0*pi*w0*exp(-alfa*t).*(bessely(1,2*w0)*
besselj(2,2*w0*exp(-alfa*t/2))-besselj(1,2*w0)*
bessely(2,2*w0*exp(-alfa*t/2)));
%aproximación 
th_a=@(t) th_0*exp(-3*alfa*t/4).*cos(2*w0*(1-exp(-alfa*t/2)));
 
hold on
fplot(th,[0,50])
fplot(th_a,[0,50])
hold off
grid on
legend('exacta','aproximada')
xlabel('t')
ylabel('\theta')
title('Péndulo de longitud variable')

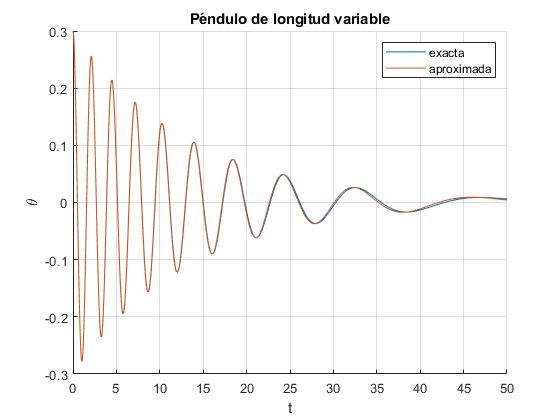
En este caso, la amplitud de la oscilación tiende rápidamente a cero.

Referencias

O. L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Oxford University Press (2010). Questions 6.18, pp. 151-156

Luis L. Sánchez-Soto, Jesús Zoido. Variations on the adiabatic invariance: The Lorentz pendulum. Am. J. Phys. 81 (1), January 2013. pp. 57-62

En este artículo se describe un dispositivo experimental

T. Wickramasinghe, R. Ochoa. Analysis of the linearity of half periods of the Lorentz pendulum. Am. J. Phys. 73 (5) May 2005, pp. 442-445