En la figura, se muestra la situación inicial. Los dos cilindros iguales de masa m_r y radio R, la plataforma horizontal de masa m_p y la partícula de masa m unida a un hilo de longitud l, que cuelga de la plataforma. Se desvía la partícula un ángulo θ₀ de la vertical y a continuación, se suelta. La posición inicial del punto de suspensión (en color rojo) está en el origen x=0. La plataforma tiene la suficiente longitud para no perder contacto con los cilindros mientras el péndulo oscila

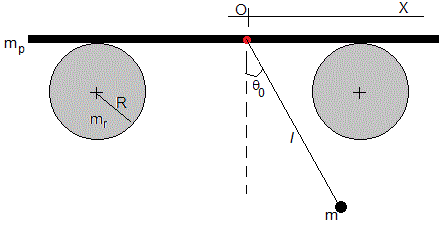
En el instante t, la partícula está desviada un ángulo θ de la vertical, el punto de suspensión se ha desplazado x, moviéndose con velocidad v=dx/dt y las ruedas giran, con velocidad angular v/R.

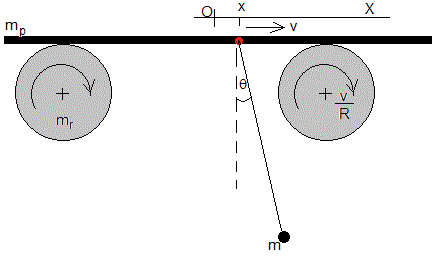
Energía del sistema

La energía cinética del sistema se compone de tres términos:

• Energía cinética de la plataforma de masa m_p que se mueve con velocidad v=dx/dt

${\displaystyle E_{k1}=\frac{1}{2}{m}_p{\left(\frac{dx}{dt}\right)}^2}$

• Energía cinética de los dos cilindros de masa m_r y radio R, momento de inercia m_rR²/2, que giran alrededor de su eje con velocidad angular v/R

${\displaystyle E_{k2}=2\left\{\frac{1}{2}\left(\frac{1}{2}{m}_r{R}^2\right){\left(\frac{v}{R}\right)}^2\right\}=\frac{1}{2}{m}_r{\left(\frac{dx}{dt}\right)}^2}$

• Energía cinética de la partícula



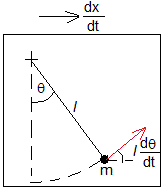
La velocidad de la partícula ldθ/dt, es tangente a su trayectoria un arco de circunferencia de radio l, tal como se muestra en la figura. Pero el punto de suspensión se mueve con velocidad v=dx/dt. Las componentes de la velocidad de la partícula para el observador inercial son

${\displaystyle \overrightarrow{v}\{\begin{array}{l}{v}_x=l\frac{d\theta }{dt}\cos \theta +\frac{dx}{dt}\\ v_y=l\frac{d\theta }{dt}\sin \theta \end{array}}$

La energía cinética de la partícula es

${\displaystyle E_{k3}=\frac{1}{2}m\left(v_x^2+v_y^2\right)=\frac{1}{2}m\left\{l^2{\left(\frac{d\theta }{dt}\right)}^2+{\left(\frac{dx}{dt}\right)}^2+2l\frac{d\theta }{dt}\frac{dx}{dt}\cos \theta \right\}}$

La energía potencial de la plataforma y de los cilindros no cambia. La energía potencial de la partícula es E_p=-mglcosθ, tomando la plataforma como nivel cero.

La energía total E=E_k1+E_k2+E_k3+E_p del sistema se conserva.

${\displaystyle E=\frac{1}{2}\left(m_p+m_r+m\right){\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}m{l}^2{\left(\frac{d\theta }{dt}\right)}^2+ml\frac{d\theta }{dt}\frac{dx}{dt}\cos \theta -mgl\cos \theta }$

Ecuaciones del movimiento

La lagrangiana L=E_k1+E_k2+E_k3-E_p

${\displaystyle L=\frac{1}{2}\left(m_p+m_r+m\right){\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}m{l}^2{\left(\frac{d\theta }{dt}\right)}^2+ml\frac{d\theta }{dt}\frac{dx}{dt}\cos \theta +mgl\cos \theta }$

Observamos que la lagrangiana L no depende de x

${\displaystyle \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)=0\frac{\partial L}{\partial \dot{x}}=\text{cte}}$

Una magnitud se mantiene constante

${\displaystyle \left(m_p+m_r+m\right)\frac{dx}{dt}+ml\cos \theta \frac{d\theta }{dt}=\text{cte}}$

En el instante t=0, la plataforma está en reposo, dx/dt=0, el péndulo, se desvía θ₀ de la vertical y se suelta, dθ/dt=0, por lo que la constante es cero

${\displaystyle \left(m_p+m_r+m\right)\frac{dx}{dt}=-ml\cos \theta \frac{d\theta }{dt}}$

Cuando la plataforma se mueve hacia la derecha dx/dt>0, el péndulo se mueve hacia la izquierda dθ/dt<0 y viceversa

Se obtiene la segunda ecuación del movimiento

${\displaystyle \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0}$

el resultado es

${\displaystyle l\frac{d^2\theta }{d{t}^2}+\cos \theta \frac{d^{2}x}{d{t}^2}+g\sin \theta =0}$

Derivamos la primera ecuación diferencial respecto del tiempo,

${\displaystyle \left(m_p+m_r+m\right)\frac{d^{2}x}{d{t}^2}+ml\cos \theta \frac{d^2\theta }{d{t}^2}-ml\sin \theta {\left(\frac{d\theta }{dt}\right)}^2=0}$

Entre estas dos últimas ecuaciones diferenciales, eliminamos d²x/dt² y despejamos d²θ/dt²

Tenemos que resolver por procedimientos numéricos, el sistema de dos ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\left\{\left(m_p+m_r+m\right)-m{\cos }^2\theta \right\}l\frac{d^2\theta }{d{t}^2}+ml\sin \theta \cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\left(m_p+m_r+m\right)g\sin \theta =0\\ \left(m_p+m_r+m\right)\frac{dx}{dt}+ml\cos \theta \frac{d\theta }{dt}=0\end{array}}$

con las condiciones iniciales siguientes: en el instante t=0, θ=θ₀, dθ/dt=0, x=0.

Nos damos cuenta, que tenemos por una parte la masa m de la partícula y por otra, la masa M=m_p+m_r (plataforma+cilindro)

${\displaystyle \{\begin{array}{l}\left(M+m{\sin }^2\theta \right)l\frac{d^2\theta }{d{t}^2}+ml\sin \theta \cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\left(M+m\right)g\sin \theta =0\\ \left(M+m\right)\frac{dx}{dt}+ml\cos \theta \frac{d\theta }{dt}=0\end{array}}$

La segunda ecuación nos relaciona el desplazamiento del punto de supensión x y el ángulo de desviación del péndulo θ

${\displaystyle dx=-\frac{ml}{m+M}\cos \theta ·d\theta }$

Integramos sabiendo que para θ=θ₀, x=0

${\displaystyle \begin{array}{l}x=-\frac{ml}{m+M}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\cos \theta ·d\theta }\\ x=\frac{ml}{m+M}\left(\sin {\theta }_0-\sin \theta \right)\end{array}}$

Por ejemplo, para l=1, m=1, M=2.5. Desviamos el péndulo θ₀=π/6 (30°) y lo soltamos. Cuando su dirección es vertical θ=0, entonces la posición del punto de suspensión, x=0.14, tal como podemos apreciar en el programa interactivo, al final de la página

Aproximaciones

Cuando el ángulo de desviación θ es pequeño hacemos las siguientes aproximaciones, cosθ≈1 y sinθ≈θ, sin²θ≈0, θ·(dθ/dt)²≈0. La primera ecuación diferencial se convierte en

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{M+m}{M}\frac{g}{l}\theta =0}$

que es la ecuación diferencial de un Movimiento Armónico Simple de frecuencia angular ω y periodo P=2π/ω

${\displaystyle {\omega }^2=\frac{M+m}{M}\frac{g}{l}}$

La solución de esta ecuación diferencial con las condiciones iniciales especificadas: t=0, θ=θ₀, dθ/dt=0, es

θ=θ₀cos(ωt)

La segunda ecuación diferencial se escribe

${\displaystyle \frac{dx}{dt}=\frac{ml}{M+m}\omega ·{\theta }_0\sin \left(\omega t\right)}$

Integramos esta ecuación, con la condición inicial, t=0, x=0

${\displaystyle x=\frac{ml}{M+m}\omega ·{\theta }_0{\displaystyle \underset{0}{\overset{t}{\int }}\sin \left(\omega t\right)dt=\frac{ml}{M+m}{\theta }_0\left(1-\cos \left(\omega t\right)\right)}}$

Solución numérica

Consideremos el sistema formado por

• Una partícula de masa m=1, que cuelga de un hilo de longitud l=1
• Masas del cilindro+plataforma, M=2.5

El péndulo se desvía un ángulo θ₀=π/12 (15°) en el instante inicial t=0. Se representa el ángulo θ del péndulo en función del tiempo t y la posición del punto de suspensión x en función del tiempo

m=1; %masa partícula que oscila
M=2.5; %masas cilindro+plataforma
longitud=1; %longitud del péndulo
angulo=pi/12;  %desviación inicial
w=sqrt((M+m)*9.8/(M*longitud)); %frecuencia angular
tFin=4*pi/w; %dos oscilaciones
%x(2) es vy, x(1) es y, 
x0=[angulo,0,0]; %[y, vy, x]
fg=@(t,x) [x(2);(-(m+M)*9.8*sin(x(1))/longitud-m*sin(x(1))*cos(x(1))*x(2)^2)
/(M+m*sin(x(1))^2);-m*longitud*cos(x(1))*x(2)/(m+M)];
[t,x]=ode45(fg,[0,tFin],x0);

subplot(2,1,1)
hold on
plot(t, x(:,1))
fplot(@(t) angulo*cos(w*t),[0,tFin])
hold off
xlabel('t')
ylabel('\theta');
grid on
legend('exacto','aproximado','location','south')
title('Angulo del péndulo')

subplot(2,1,2)
hold on
plot(t, x(:,3))
fplot(@(t) m*longitud*angulo*(1-cos(w*t))/(m+M),[0,tFin])
hold off
xlabel('t')
ylabel('x');
legend('exacto','aproximado','location','north')
grid on
title('Posición plataforma')

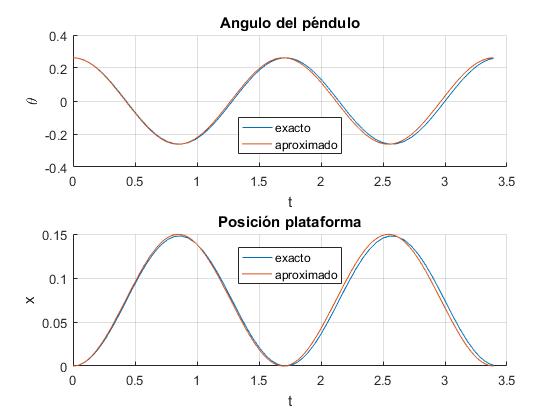
En la representación gráfica, vemos que cuando el ángulo de desviación θ₀ es pequeño, la solución numérica de las ecuaciones del movimiento se ajusta a sus aproximaciones analíticas

Comprobamos el principio de conservación de la energía, la energía inicial es E=-mglcosθ₀

>> -m*longitud*9.8*cos(pi/12)
ans =   -9.4661

Calculamos la energía en cada instante, la variable vx es dx/dt

>> vx=-m*longitud*cos(x(:,1)).*x(:,2)/(m+M);
>> E=(m+M)*vx.^2/2+m*(longitud*x(:,2)).^2/2+m*longitud*x(:,2).*vx.*cos(x(:,1))
-m*9.8*longitud*cos(x(:,1))
E =
   -9.4661
   -9.4661
   -9.4661
   ......
   -9.4665

Periodo

La energía es constante e igual a la energía inicial

${\displaystyle -mgl\cos {\theta }_0=\frac{1}{2}\left(M+m\right){\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}m{l}^2{\left(\frac{d\theta }{dt}\right)}^2+ml\frac{d\theta }{dt}\frac{dx}{dt}\cos \theta -mgl\cos \theta }$

La lagrangiana L no depende de la variable x, por tanto, hay otra constante del movimiento

${\displaystyle \left(M+m\right)\frac{dx}{dt}+ml\cos \theta \frac{d\theta }{dt}=0}$

Despejamos dx/dt en la segunda ecuación y sustituimos en la primera. Despejamos dθ/dt

${\displaystyle \frac{d\theta }{dt}=\sqrt{\frac{2g}{l}\frac{m+M}{m{\sin }^2\theta +M}\left(\cos \theta -\cos {\theta }_0\right)}}$

Integramos la variable θ entre 0 y θ₀ para obtener un cuarto de periodo

${\displaystyle \begin{array}{l}\sqrt{\frac{l}{2g\left(m+M\right)}}{\displaystyle \underset{0}{\overset{{\theta }_0}{\int }}\sqrt{\frac{m{\sin }^2\theta +M}{\cos \theta -\cos {\theta }_0}}d\theta =\frac{P}{4}}\\ P=2\sqrt{\frac{2l}{g\left(m+M\right)}}{\displaystyle \underset{0}{\overset{{\theta }_0}{\int }}\sqrt{\frac{m{\sin }^2\theta +M}{\cos \theta -\cos {\theta }_0}}d\theta }\end{array}}$

La función integral de MATLAB calcula, empleando procedimientos numéricos, la integral definida

m=1; %masa partícula que oscila
M=2.5*m; %masas cilindro+plataforma
longitud=1; %longitud del péndulo
angulo=pi/6;  %desviación inicial

f=@(x) sqrt((m*sin(x).^2+M)./(cos(x)-cos(angulo)));
P=2*sqrt(2*longitud/(9.8*(m+M)))*integral(f,0, angulo);
disp(P)

    1.7693

Actividades

Se introduce

• La suma de las masas del cilindro y la plataforma M en el control titulado Masas plataforma+cilindro
• El ángulo inicial de desviación del péndulo θ₀ en el control titulado Angulo inicial
• La masa de la partícula se ha fijado en m=1
• La longitud del péndulo se ha fijado en l=1

Se pulsa el botón titulado Nuevo

Observamos el movimiento del péndulo, la plataforma y los cilindros. Se proporciona los valores:

• El tiempo t
• La posición del punto de suspensión x
• El ángulo de desviación θ en grados, del péndulo respecto de la vertical

El lector puede medir el periodo de la oscilación utilizando los botones Pausa || y Paso a paso >|

El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente

${\displaystyle \left|\frac{E-E_0}{E_0}\right|·100}$

donde E es la energía del sistema en cualquier instante t, y E₀ es la energía inicial del sistema.

Este valor se proporciona en caracteres de color rojo en la parte inferior derecha. Su valor debe ser siempre cero, o un valor muy pequeño lo que indica que la energía del sistema permanece constante y el programa realiza los cálculos correctamente.