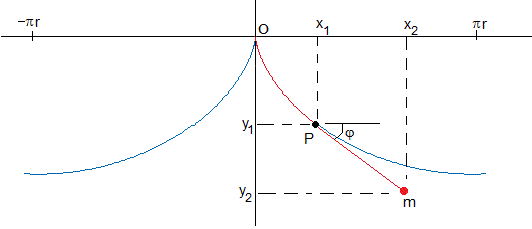
En la figura, las curvas de color azul son cicloides. En color rojo se muestra el péndulo oscilando entre ambas superficies. El hilo se apadpta a la superficie de la cicloide hasta el punto P, desde este punto hasta el extremo su forma es la de es un segumento de recta tangente a la cicliode en el punto P.

Vamos a determinar las coordendas de la masa puntual puntual m, para escribir las ecuaciones del movimiento y verificar que su periodo de oscilación es independiente de la amplitud.

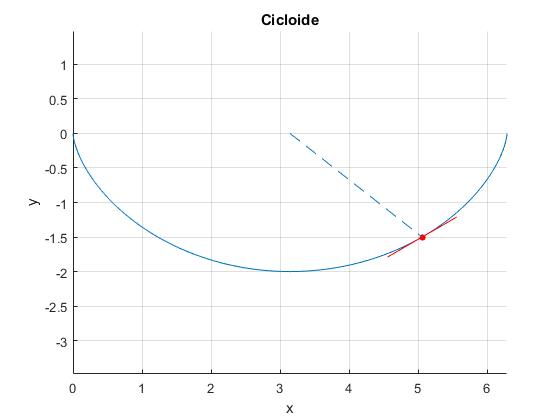
La cicloide y su tangente en P

Las ecuaciones de la cicloide son

x=r(θ-sinθ)
y=r(cosθ-1)

Dando valores al parámetro θ entre 0 y 2π representamos el arco completo de color azul en la figura. El vértice de la cicloide se obtiene para θ=π, sus coordenadas son (πr, -2r)

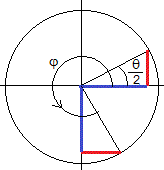
La tangente a la cicloide en un punto P, forma un ángulo φ con la horizontal. El parámetro θ y el ángulo φ están relacionados

${\displaystyle \begin{array}{l}\tan \phi =\frac{dy}{dx}=-\frac{\sin \theta }{1-\cos \theta }=-\frac{\cos \left(\theta /2\right)}{\sin \left(\theta /2\right)}=-\frac{1}{\tan \left(\theta /2\right)}\\ \phi =\frac{3\pi }{2}+\frac{\theta }{2}\end{array}}$

r=1;
x=@(t) r*(t-sin(t));
y=@(t) r*(cos(t)-1);
hold on
fplot(x,y,[0,2*pi])
t=pi+pi/3; %posición del punto P
x0=r*(t-sin(t));
y0=r*(cos(t)-1);
plot(x0,y0,'o', 'markersize',4,'markeredgecolor','r',
'markerfacecolor','r')
phi=3*pi/2+t/2;
%tangente a la cicliode en P
f=@(x) tan(phi)*(x-x0)+y0;
fplot(f,[x0-0.5,x0+0.5], 'color','r')
line([pi*r,x0],[0,y0],'lineStyle','--')
hold off
axis equal
grid on
xlabel('x'); 
ylabel('y')
title('Cicloide')

Longitud del arco de cicloide entre O y P

En un instante dado t, vamos a determinar la longitud l₁ del hilo entre el punto de suspensión O y P.

${\displaystyle \begin{array}{l}{l}_1={\displaystyle \underset{0}{\overset{x_1}{\int }}\sqrt{d{x}^2+d{y}^2}=}r{\displaystyle \underset{0}{\overset{{\theta }_1}{\int }}\sqrt{{\left(1-\cos \theta \right)}^2+{\sin }^2\theta }d\theta =}\sqrt{2}r{\displaystyle \underset{0}{\overset{{\theta }_1}{\int }}\sqrt{\left(1-\cos \theta \right)}d\theta =}\\ 2r{\displaystyle \underset{0}{\overset{{\theta }_1}{\int }}\sin \frac{\theta }{2}d\theta =4}r\left(1-\cos \frac{{\theta }_1}{2}\right)\end{array}}$

Posición del extremo del péndulo

Las coordendas (x₁, y₁) del punto P de la cicloide son

x₁=r(θ₁-sinθ₁)
y₁=r(cosθ₁-1)

La longitud del segmento entre P y el extremo de la cuerda es l-l₁ y hace un ángulo φ₁ con la horizontal, que es el ángulo que forma la recta tangente a la cicloide en el punto P con la horizontal, tal como puede verse en la primera figura

${\displaystyle \tan {\phi }_1=\frac{dy}{dx}=-\frac{\sin {\theta }_1}{1-\cos {\theta }_1}=-\frac{\cos \left({\theta }_1/2\right)}{\sin \left({\theta }_1/2\right)}}$

Las coordenadas de la masa puntual m son

${\displaystyle \{\begin{array}{l}{x}_2=x_1+(l-l_1)\cos {\phi }_1\\ y_2=y_1+(l-l_1)\sin {\phi }_1\end{array}}$

Prescindiendo de subíndices, la posición (x,y) de la masa puntual m, depende de un parámetro θ de la siguiente manera

${\displaystyle \{\begin{array}{l}x=r\left(\theta +\sin \theta \right)+\left(l-4r\right)\sin \left(\theta /2\right)\\ y=-r\left(\cos \theta +3\right)-\left(l-4r\right)\cos \left(\theta /2\right)\end{array}}$

Derivando con respecto al tiempo, obtenemos las componentes de la velocidad

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=\left(r\left(1+\cos \theta \right)+\frac{1}{2}\left(l-4r\right)\cos \left(\frac{\theta }{2}\right)\right)\frac{d\theta }{dt}\\ \frac{dy}{dt}=\left(r\sin \theta +\frac{1}{2}\left(l-4r\right)\sin \left(\frac{\theta }{2}\right)\right)\frac{d\theta }{dt}\end{array}}$

La energía cinética T es

${\displaystyle \begin{array}{l}T=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2\right)=\\ \frac{1}{2}m\left(2r^2\left(1+\cos \theta \right)+\frac{1}{4}{\left(l-4r\right)}^2+2r\left(l-4r\right)\cos \left(\frac{\theta }{2}\right)\right){\left(\frac{d\theta }{dt}\right)}^2\end{array}}$

La energía potencial es V=mgy

${\displaystyle V(\theta )=-mgr(\cos \theta +3)-mg(l-4r)\cos \left(\frac{\theta }{2}\right)}$

Ecuación del movimiento

Calculamos la lagrangiana L=T-V y la ecuación del movimiento

${\displaystyle \begin{array}{l}L=\frac{1}{2}m\left(2r^2\left(1+\cos \theta \right)+\frac{1}{4}{\left(l-4r\right)}^2+2r\left(l-4r\right)\cos \left(\frac{\theta }{2}\right)\right){\left(\frac{d\theta }{dt}\right)}^2+mgr(\cos \theta +3)+mg(l-4r)\cos \left(\frac{\theta }{2}\right)\\ L=\frac{1}{2}m\left(2r^2\left(1+\cos \theta \right)+\frac{1}{4}{\left(l-4r\right)}^2+2r\left(l-4r\right)\cos \left(\frac{\theta }{2}\right)\right){\dot{\theta }}^2+mgr(\cos \theta +3)+mg(l-4r)\cos \left(\frac{\theta }{2}\right)\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ 2\left(r^2\left(1+\cos \theta \right)+\frac{1}{8}{\left(l-4r\right)}^2+r\left(l-4r\right)\cos \left(\frac{\theta }{2}\right)\right)\frac{d^2\theta }{d{t}^2}-\\ \left(r^2\sin \theta +\frac{1}{2}r\left(l-4r\right)\sin \left(\frac{\theta }{2}\right)\right){\left(\frac{d\theta }{dt}\right)}^2+gr\sin \theta +\frac{1}{2}g(l-4r)\sin \left(\frac{\theta }{2}\right)=0\end{array}}$

Resolvemos la ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: t=0; θ=θ₀, dθ/dt=0.

r=1; %cicloide
L=2*r; %longitud del péndulo
x0=[pi/3,0];
%x(1)=theta, x(2)=dtheta/dt
f=@(t,x) [x(2); ((r*r*sin(x(1))+r*(L-4*r)*sin(x(1)/2)/2)*x(2)^2
-(9.8*r*sin(x(1))+9.8*(L-4*r)*sin(x(1)/2)/2))/(2*r*r*(1+cos(x(1)))+
(L-4*r)*(L-4*r)/4+2*r*(L-4*r)*cos(x(1)/2))]; 
tspan=[0,10];
[t,x]=ode45(f,tspan,x0);

plot(t,x(:,1))
grid on
xlabel('t')
ylabel('\theta');
title('Péndulo')
% energía total 
en=(r^2*(1+cos(x(:,1)))+(L-4*r)^2/8+r*(L-4*r)*cos(x(:,1)/2)).*x(:,2).^2
-9.8*r*(cos(x(:,1))+3)-9.8*(L-4*r)*cos(x(:,1)/2);

Comprobamos en la última línea de este código, que la energía T+V permanece constante en todos los puntos de la trayectoria

>> en
en =
  -17.3259
  -17.3259
  -17.3259
  -17.3259
  ....

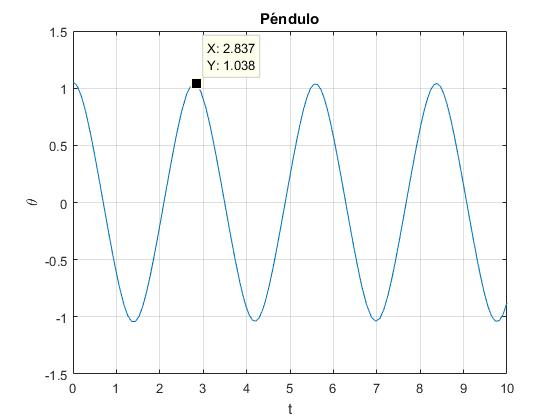
Con Data cursor, en el menú de iconos de la ventana gráfica, medimos el periodo del péndulo para diferentes condiciones iniciales, modificando el parámetro θ₀ o la longitud del péndulo que en este caso ha sido 2r

Caso particular l=4r

El caso particular más interesante se produce cuando la longitud del péndulo es l=4r

Las coordendas (x,y) de masa puntual m son

${\displaystyle \{\begin{array}{l}x=r\left(\theta +\sin \theta \right)\\ y=-r\left(\cos \theta +3\right)\end{array}}$

La energía cinética T es

${\displaystyle T=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2\right)=m{r}^2\left(1+\cos \theta \right){\left(\frac{d\theta }{dt}\right)}^2}$

La energía potencial de la masa puntual es V=mgy=-mgr(3+cosθ)

${\displaystyle \begin{array}{l}L=T-V=m{r}^2\left(1+\cos \theta \right){\left(\frac{d\theta }{dt}\right)}^2+mgr\left(3+\cos \theta \right)\\ L=m{r}^2\left(1+\cos \theta \right){\dot{\theta }}^2+mgr\left(3+\cos \theta \right)\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ 2m{r}^2\left(1+\cos \theta \right)\frac{d^2\theta }{d{t}^2}-m{r}^2\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+mgr\sin \theta =0\\ \frac{d^2\theta }{d{t}^2}=\frac{1}{2}\left({\left(\frac{d\theta }{dt}\right)}^2-\frac{g}{r}\right)\tan \left(\frac{\theta }{2}\right)\end{array}}$

r=1; %cicloide
x0=[pi/3,0];
%x(1)=theta, x(2)=dtheta/dt
f=@(t,x) [x(2);(x(2)^2-9.8/r)*tan(x(1)/2)/2]; 
tspan=[0,10];
[t,x]=ode45(f,tspan,x0);

plot(t,x(:,1))
grid on
xlabel('t')
ylabel('\theta');
title('Péndulo')
%la energía total es constante
en=r^2*(1+cos(x(:,1))).*x(:,2).^2-9.8*r*(3+cos(x(:,1)));

Comprobamos en la última línea de este código, que la energía T+V permanece constante en todos los puntos de la trayectoria

>> en
>> en
  -34.3000
  -34.3000
  -34.3000
  -34.3000
  ....

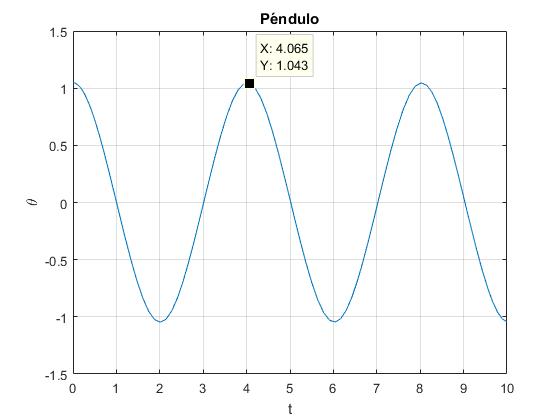
Periodo del péndulo, l=4r

Calculamos mediante la expresión de la energía el periodo del péndulo para este caso particular de un péndulo de longitud l=4r

La energía total de la masa puntual es constante e igual a la inicial cuando se encuentra en uno de los extremos de la oscilación, el parámetro θ=θ₀ y dθ/dt=0

${\displaystyle \begin{array}{l}m{r}^2\left(1+\cos \theta \right){\left(\frac{d\theta }{dt}\right)}^2-mgr\left(3+\cos \theta \right)=-mgr\left(3+\cos {\theta }_0\right)\\ \frac{d\theta }{dt}=\sqrt{\frac{g\left(\cos \theta -\cos {\theta }_0\right)}{r\left(1+\cos \theta \right)}}\end{array}}$

El tiempo t que tarda el péndulo en describir un cuarto de oscilación es el que le lleva a la masa puntual a desplazarse desde el centro θ=0 hasta el extremo θ=θ₀

${\displaystyle {\displaystyle \underset{0}{\overset{t}{\int }}dt}={\displaystyle \underset{0}{\overset{{\theta }_0}{\int }}\sqrt{\frac{r\left(1+\cos \theta \right)}{g\left(\cos \theta -\cos {\theta }_0\right)}d\theta }}}$

El periodo P es cuatro veces este tiempo

${\displaystyle P=4\sqrt{\frac{r}{g}}{\displaystyle \underset{0}{\overset{{\theta }_0}{\int }}\sqrt{\frac{\left(1+\cos \theta \right)}{\left(\cos \theta -\cos {\theta }_0\right)}}d\theta }}$

Para calcular la integral, hacemos la sustitución z=(cosθ-cosθ₀)/(1-cosθ₀)

${\displaystyle P=-4\sqrt{\frac{r}{g}}{\displaystyle \underset{1}{\overset{0}{\int }}\frac{dz}{\sqrt{z-z^2}}}}$

Para calcular esta última integral, completamos cuadrados en el denominador

${\displaystyle {\displaystyle \underset{0}{\overset{1}{\int }}\frac{dz}{\sqrt{z-z^2}}=}2{\displaystyle \underset{0}{\overset{1}{\int }}\frac{dz}{\sqrt{1-{(2z-1)}^{{}^2}}}=2{\displaystyle \underset{-1}{\overset{1}{\int }}\frac{ds}{\sqrt{1-s^2}}=}}{2\arcsin s|}_{-1}^1=\pi }$

>> syms x;
>> int('1/sqrt(x-x^2)',x,0,1)
ans =pi

El periodo P es constante e independiente de la amplitud

${\displaystyle P=4\pi \sqrt{\frac{r}{g}}}$

Para r=1, el periodo P=4.0142 s

Actividades

Se introduce

• El parámetro θ₀ en el control titulado Parámetro

• La longitud l del péndulo en unidades del parámetro r de la cicloide en el control titulado Longitud

• El valor del parámetro r=1 se ha fijado en el programa interactivo

Se pulsa el botón titulado Nuevo

El caso más interesante se produce cuando l=4r

El programa resuelve la ecuación diferencial por procedimientos numéricos, calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente

${\displaystyle \left|\frac{E-E_0}{E_0}\right|·100}$

donde E es la energía del sistema en cualquier instante t, y E₀ es la energía inicial del sistema.

Este valor se proporciona en caracteres de color rojo en la parte inferior izquierda. Su valor debe ser siempre cero, o un valor muy pequeño lo que indica que la energía del sistema permanece constante y el programa realiza los cálculos correctamente.

Oscilaciones isócronas

Consideremos una partícula de masa m que se mueve a lo largo del eje X, bajo la acción de una fuerza conservativa cuya energía potencial es

${\displaystyle E_p(x)=\epsilon {\left(1-\sqrt{1+\frac{x}{\sigma }}\right)}^2}$

donde ε y σ son constantes, se tienen que cumplir x/σ≥-1

La conservación de la energía se escribe

${\displaystyle \frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+\epsilon {\left(1-\sqrt{1+\frac{x}{\sigma }}\right)}^2=E}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}\xi =\frac{x}{\sigma },\tau =\frac{1}{\sigma }\sqrt{\frac{\epsilon }{m}}t\\ \frac{1}{2}m\frac{{\sigma }^2}{\frac{{\sigma }^{2}m}{\epsilon }}{\left(\frac{d\xi }{d\tau }\right)}^2+\epsilon {\left(1-\sqrt{1+\xi }\right)}^2=E\\ {\left(\frac{d\xi }{d\tau }\right)}^2+2{\left(1-\sqrt{1+\xi }\right)}^2=\frac{2E}{\epsilon }\end{array}}$

La velocidad de la partícula se hace cero, para dos posiciones de retorno

${\displaystyle \begin{array}{l}\left(1-\sqrt{1+\xi }\right)=\pm \sqrt{\frac{E}{\epsilon }}\\ \sqrt{1+\xi }=1\pm \sqrt{\frac{E}{\epsilon }}\\ {\xi }_1={\left(1-\sqrt{\frac{E}{\epsilon }}\right)}^2-1=\frac{E}{\epsilon }-2\sqrt{\frac{E}{\epsilon }}\\ {\xi }_2={\left(1+\sqrt{\frac{E}{\epsilon }}\right)}^2-1=\frac{E}{\epsilon }+2\sqrt{\frac{E}{\epsilon }}\end{array}}$

Representamos la energía potencial en función de x/σ, para ε=1 y σ=1.

sigma=1;
epsilon=1;
E=0.4; %energía
x2=(1+sqrt(E/epsilon))^2-1;
x1=(1-sqrt(E/epsilon))^2-1;
f=@(x) epsilon*(1-sqrt(1+x/sigma)).^2;
fplot(f,[-1,3])
line([-1,3],[E,E])
line([x1,x1], [0,E],'lineStyle','--')
line([x2,x2], [0,E],'lineStyle','--')
grid on
xlabel('x/\sigma')
ylabel('E_p(x)/\epsilon')
title('Energía potencial')

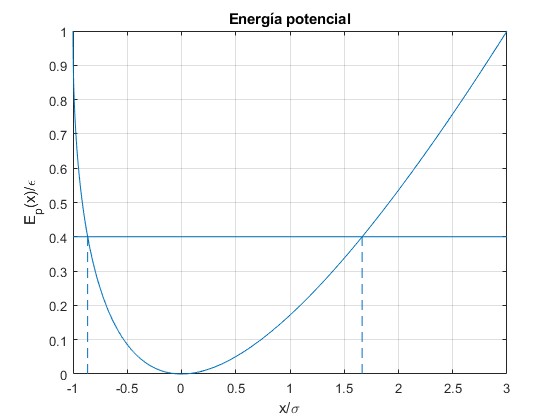
para la energía E=0.4. las posiciones de retorno son: ξ₂=1.6649, ξ₁=-0.8649

>> x2,x1
x2 =    1.6649
x1 =   -0.8649

señaladas por líneas a trazos verticales

Integramos la ecuación diferencial haciendo un cambio de variable

${\displaystyle \begin{array}{l}{\left(\frac{d\xi }{d\tau }\right)}^2+2{\left(1-\sqrt{1+\xi }\right)}^2=\frac{2E}{\epsilon }\\ 1-\sqrt{1+\xi }=\sqrt{\frac{E}{\epsilon }}\cos \theta \\ \xi ={\left(1-\sqrt{\frac{E}{\epsilon }}\cos \theta \right)}^2-\mathrm{1,}d\xi =2\left(1-\sqrt{\frac{E}{\epsilon }}\cos \theta \right)\sqrt{\frac{E}{\epsilon }}\sin \theta ·d\theta \\ {\left(\frac{d\xi }{d\tau }\right)}^2+\frac{2E}{\epsilon }{\cos }^2\theta =\frac{2E}{\epsilon }\\ \frac{d\xi }{d\tau }=\pm \sqrt{\frac{2E}{\epsilon }}\sin \theta \\ \frac{2\left(1-\sqrt{\frac{E}{\epsilon }}\cos \theta \right)\sqrt{\frac{E}{\epsilon }}\sin \theta ·d\theta }{d\tau }=\pm \sqrt{\frac{2E}{\epsilon }}\sin \theta \\ d\tau =\pm \sqrt{2}\left(1-\sqrt{\frac{E}{\epsilon }}\cos \theta \right)d\theta \end{array}}$

Integramos el tiempo τ

${\displaystyle \tau =\sqrt{2}\left(\theta -\sqrt{\frac{E}{\epsilon }}\sin \theta \right)+C}$

Se calcula la constante de integración C a partir de las condiciones iniciales

En el instante τ=0, la partícula parte de ξ₂>0 o θ=π, por lo que $C=-\sqrt{2}\pi$

${\displaystyle \tau =\sqrt{2}\left(\theta -\sqrt{\frac{E}{\epsilon }}\sin \theta -\pi \right),\theta \ge \pi }$

En el instante Τ/2 la partícula llega a la posición de retorno ξ₁<0, o θ=2π completándose medio periodo

${\displaystyle \begin{array}{l}\frac{{\rm T}}{2}=\sqrt{2}\pi \\ {\rm T}=2\sqrt{2}\pi =\mathrm{8.8858.}\end{array}}$

Representamos la posición ξ en función del tiempo τ ambas dependientes del parámetro θ comprendido entre π y 8π

${\displaystyle \{\begin{array}{l}\tau =\sqrt{2}\left(\theta -\sqrt{\frac{E}{\epsilon }}\sin \theta -\pi \right),\theta \ge \pi \\ \xi ={\left(1-\sqrt{\frac{E}{\epsilon }}\cos \theta \right)}^2-1\end{array}}$

epsilon=1;
hold on
for E=[1, 0.1]
    xi=@(th) (1-sqrt(E/epsilon)*cos(th)).^2-1;
    tau=@(th) sqrt(2)*(th-sqrt(E/epsilon)*sin(th)-pi);
    fplot(tau, xi, [pi,8*pi])
end
hold off
grid on
xlabel('\tau')
legend('1','0.1','location','best')
ylabel('xi')
title('Posición')

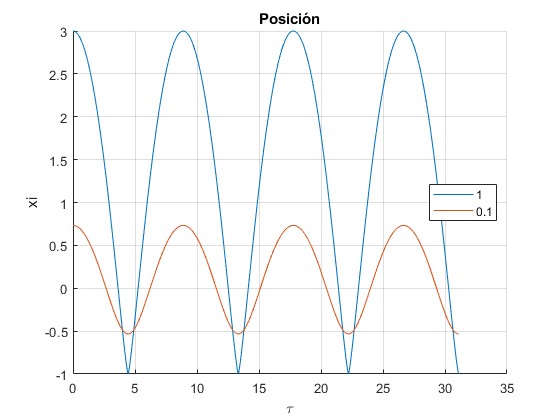
La osiclación se repite cada periodo Τ=8.8858

Ecuación del movimiento

Derivamos respecto de τ la conservación de la energía

${\displaystyle \begin{array}{l}{\left(\frac{d\xi }{d\tau }\right)}^2+2{\left(1-\sqrt{1+\xi }\right)}^2=\frac{2E}{\epsilon }\\ 2\left(\frac{d\xi }{d\tau }\right)\frac{d^2\xi }{d{\tau }^2}-4\left(1-\sqrt{1+\xi }\right)\frac{1}{2\sqrt{1+\xi }}\frac{d\xi }{d\tau }=0\\ \frac{d^2\xi }{d{\tau }^2}+\left(1-\frac{1}{\sqrt{1+\xi }}\right)=0\end{array}}$

Resolvemos la ecuación diferencial por el procedimiento ode45 de MATLAB para una partícula de energía E=0.4, con las siguientes condiciones iniciales, la partícula parte en reposo de la posición ξ₂>0

epsilon=1;
E=0.4; %energía
x2=(1+sqrt(E/epsilon))^2-1;
f=@(t,x) [x(2);1/sqrt(1+x(1))-1]; 
[t,x]=ode45(f,[0,20],[x2,0]);
plot(t,x(:,1))
grid on
xlabel('\tau')
ylabel('\xi');
title('Oscilador isócrono')

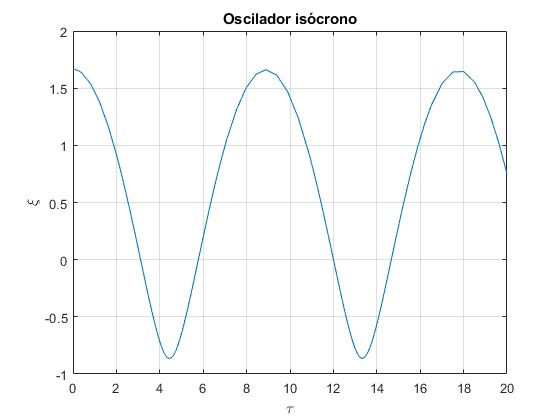
Para oscilaciones de amplitud pequeña

>> syms x;
>> taylor(1-1/sqrt(1+x),x)
ans =(63*x^5)/256 - (35*x^4)/128 + (5*x^3)/16 - (3*x^2)/8 + x/2

${\displaystyle \begin{array}{l}\frac{d^2\xi }{d{\tau }^2}+\frac{\xi }{2}=0\\ {\omega }_0^2=\frac{1}{2},P=\frac{2\pi }{{\omega }_0}=2\pi \sqrt{2}\end{array}}$

Referencias

Pirooz Mohazzabi. Isochronous anharmonic oscillations. Can. J. Phys 76: 645–657 (1998)