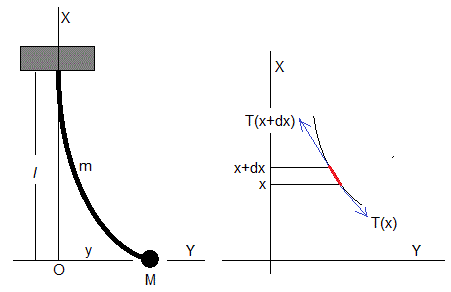
El péndulo que se estudia en esta página, consiste en una partícula de masa M unida a una cuerda de longitud l y masa m y densidad uniforme m/l. El origen y los ejes se muestran en la figura. El punto de suspensión tiene de coordenadas x=l, e y=0. La partícula oscila a lo largo del eje horizontal Y con una frecuencia angular ω que deduciremos en esta página, de forma y=Asin(ωt+φ), donde A es la amplitud y φ es la fase inicial, ambas dependientes de las condiciones iniciales

La deducción de la ecuación del movimiento de un elemento de la cuerda (señalado en color rojo en la figura de la derecha) es similar a la de las ondas transversales en una cuerda, la diferencia es que la tensión de la cuerda es constante y aquí la tensión de la cuerda en la posición x es el peso de la partícula más la parte de la cuerda por debajo de x.

T(x)=(M+mx/l)g

Consideremos una porción de cuerda comprendida entre x y x+dx

• T(x), es la fuerza que ejerce la parte de abajo de la cuerda sobre el elemento diferencial
• T(x+dx), es la fuerza que ejerce la parte de arriba de la cuerda sobre el elemento diferencial

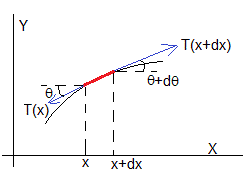
Para deducir la ecuación del movimiento del elemento diferencial de la cuerda giramos los ejes, tal como se muestra en la figura

La componente Y de las fuerzas, dF_y, que actúan sobre dicho elemento diferencial de masa m·dx/l es

${\displaystyle \begin{array}{l}d{F}_y=T(x+dx)·\sin (\theta +d\theta )-T(x)\sin \theta \simeq \\ \left(T(x)+\frac{dT}{dx}dx\right)·(\sin \theta +\cos \theta ·d\theta )-T(x)\sin \theta =\\ \frac{d}{dx}\left(\sin \theta ·T(x)\right)·dx\simeq \frac{d}{dx}\left(\tan \theta ·T(x)\right)·dx=\frac{d}{dx}\left(\frac{dy}{dx}·T(x)\right)·dx\end{array}}$

Para ángulos pequeños, hacemos la aproximación sinθ≈tanθ

Esta componente dF_y de fuerza sobre el elemento diferencial de masa m·dx/l produce una aceleración a lo largo del eje Y. En un Movimiento Armónico Simple, la aceleración -ω²y es proporcional al desplazamiento y

${\displaystyle \begin{array}{l}\frac{d}{dx}\left(\frac{dy}{dx}\left(M+\frac{m}{l}x\right)g\right)dx=\left(\frac{m}{l}dx\right)\left(-{\omega }^{2}y\right)\\ \frac{d}{dx}\left(\frac{dy}{dx}\left(\frac{M}{m}l+x\right)\right)+\frac{{\omega }^2}{g}y=0\end{array}}$

Haciendo el cambio de variable

${\displaystyle \begin{array}{l}z=2\sqrt{\frac{M}{m}l+x}\\ \frac{dy}{dx}=\frac{dy}{dz}\frac{dz}{dx}=\frac{2}{z}\frac{dy}{dz}\end{array}}$

El primer miembro de la ecuación diferencial se escribe, en términos de la nueva variable z

${\displaystyle \frac{d}{dx}\left(\frac{dy}{dx}\frac{z^2}{4}\right)=\frac{d}{dx}\left(\frac{dy}{dz}\frac{z}{2}\right)=\frac{d}{dz}\left(\frac{dy}{dz}\frac{z}{2}\right)\frac{dz}{dx}=\frac{d}{dz}\left(\frac{dy}{dz}\frac{z}{2}\right)\frac{2}{z}=\frac{1}{z}\frac{dy}{dz}+\frac{d^{2}y}{d{z}^2}}$

Finalmente, llegamos a la ecución diferencial de Bessel con n=0

${\displaystyle z^2\frac{d^{2}y}{d{z}^2}+z\frac{dy}{dz}+\frac{{\omega }^2}{g}{z}^{2}y=0}$

La solución de la ecuación diferencial es

${\displaystyle y=A{J}_0\left(\sqrt{\frac{{\omega }^2}{g}}z\right)+B{Y}_0\left(\sqrt{\frac{{\omega }^2}{g}}z\right)}$

o bien,

${\displaystyle y=A{J}_0(\xi )+B{Y}_0(\xi )\xi =2\frac{\omega }{{\omega }_0}\sqrt{\frac{M}{m}+\frac{x}{l}}{\omega }_0=\sqrt{\frac{g}{l}}}$

• ω₀ es la frecuencia angular del péndulo simple de longitud l y masa despreciable en la aproximación de oscilaciones de amplitud pequeña.
• ω es la frecuencia angular del péndulo formado por una partícula de masa M unida a una cuerda de longitud l y masa m
• J₀ e Y₀ son las funciones de Bessel de orden cero y de primera y segunda especie, respectivamente.
• A y B son dos coeficientes que se determinan a partir de las condiciones iniciales y de contorno

Condiciones de contorno

• El punto de suspensión se encuentra en x=l y=0, o bien ${\xi }_l=2\frac{\omega }{{\omega }_0}\sqrt{1+\frac{M}{m}}$

La primera ecuación es

${\displaystyle A{J}_0\left({\xi }_l\right)+B{Y}_0\left({\xi }_l\right)=0}$

• Para x=0, o bien para ${\xi }_0=2\frac{\omega }{{\omega }_0}\sqrt{\frac{M}{m}}$, la tensión de la cuerda T(0)=Mg, es el peso de la partícula, su componente a lo largo del eje Y es

${\displaystyle T(0)·\sin \theta \simeq T(0)·\tan \theta =Mg{\left(\frac{dy}{dx}\right)}_{x=0}}$

hace que la partícula de masa M describa un MAS de frecuencia angular ω

${\displaystyle Mg{\left(\frac{dy}{dx}\right)}_{x=0}=-M{\omega }^{2}y}$

Sabiendo que las derivadas de las funciones de Bessel J₀ e Y₀ son

${\displaystyle \begin{array}{l}\frac{d}{dx}{J}_0(x)=-J_1(x)\\ \frac{d}{dx}{Y}_0(x)=-Y_1(x)\end{array}}$

>> syms x;
>> diff(besselj(0,x))
ans =-besselj(1, x)
>> diff(bessely(0,x))
ans =-bessely(1, x)

La segunda ecuación es

${\displaystyle \begin{array}{l}g{\left(\frac{d\xi }{dx}\right)}_{x=0}\left(A{J}_1({\xi }_0)+B{Y}_1({\xi }_0)\right)={\omega }^2\left(A{J}_0({\xi }_0)+B{Y}_0({\xi }_0)\right)\\ A\left(J_1({\xi }_0)-\frac{\omega }{{\omega }_0}\sqrt{\frac{M}{m}}{J}_0({\xi }_0)\right)+B\left(Y_1({\xi }_0)-\frac{\omega }{{\omega }_0}\sqrt{\frac{M}{m}}{Y}_0({\xi }_0)\right)=0\end{array}}$

Eliminando A y B del sistema homogéneo de dos ecuaciones, obtenemos la ecuación trascendente

${\displaystyle \frac{\omega }{{\omega }_0}\sqrt{\frac{M}{m}}\left\{Y_0\left({\xi }_l\right)·J_0\left({\xi }_0\right)-J_0\left({\xi }_l\right)·Y_0\left({\xi }_0\right)\right\}=Y_0\left({\xi }_l\right)·J_1\left({\xi }_0\right)-J_0\left({\xi }_l\right)·Y_1\left({\xi }_0\right)}$

Dado el cociente entre la masa de la cuerda y la masa de la partícula, k=m/M, calculamos las raíces de la ecuación trascendente f(x) para obtener la frecuencia angular x=ω/ω₀ de la oscilación del péndulo.

${\displaystyle \begin{array}{l}\frac{x}{\sqrt{k}}\left\{Y_0\left(2x\sqrt{1+\frac{1}{k}}\right)·J_0\left(2\frac{x}{\sqrt{k}}\right)-J_0\left(2x\sqrt{1+\frac{1}{k}}\right)·Y_0\left(2\frac{x}{\sqrt{k}}\right)\right\}\\ -Y_0\left(2x\sqrt{1+\frac{1}{k}}\right)·J_1\left(2\frac{x}{\sqrt{k}}\right)+J_0\left(2x\sqrt{1+\frac{1}{k}}\right)·Y_1\left(2\frac{x}{\sqrt{k}}\right)=0\end{array}}$

En este script, representamos la función trascendente f(x) para un valor dado del cociente k=m/M, para estimar la primera raíz, cuyo valor calculamos con fzero

k=2;
f=@(x)(bessely(0,2*x*sqrt(1+1/k)).*besselj(0,2*x/sqrt(k))-
besselj(0,2*x*sqrt(1+1/k)).*bessely(0,2*x/sqrt(k))).*x/sqrt(k)-
bessely(0,2*x*sqrt(1+1/k)).*besselj(1,2*x/sqrt(k))+
besselj(0,2*x*sqrt(1+1/k)).*bessely(1,2*x/sqrt(k));
fplot(f,[0.1,15])
grid on
ylim([-1,1])
xlabel('x')
ylabel('f(x)')
title('gráfica de f(x)')

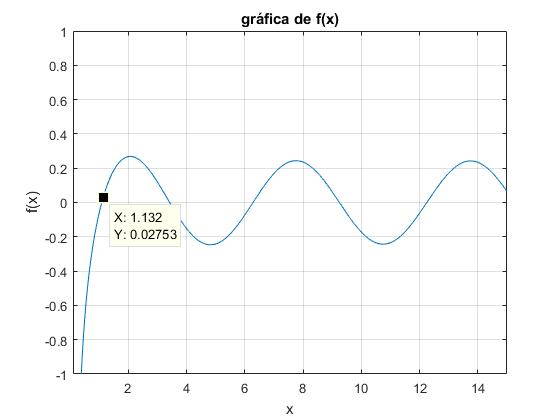
>> fzero(f,1.1)
ans =    1.0867

Péndulo compuesto

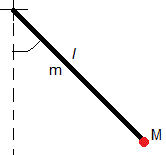
Si la cuerda es rígida tenemos un péndulo compuesto formado por una varilla de masa m y longitud l con una partícula de masa M pegada a su extremo, el otro extremo de la varilla es el punto de suspensión

El periodo o la frecuencia angular de las oscilaciones de pequeña amplitud es

${\displaystyle {\omega }^2=\frac{(m+M)gx}{I_0}}$

Donde I₀ es el momento de inercia del péndulo respecto a un eje perpendicular al plano de oscilación del péndulo y que pasa por el punto de suspensión O, x es la posición del centro de masa respecto del mismo punto

${\displaystyle \begin{array}{l}x=\frac{m\frac{l}{2}+Ml}{m+M}\\ I_O=\frac{1}{3}m{l}^2+M{l}^2\\ \omega ={\omega }_0\sqrt{\frac{3m/M+6}{2m/M+6}}\end{array}}$

Para k=m/M=2, ω=1.095ω₀

Creamos un script para comparar las frecuencias ω/ω₀ de oscilación de una varilla en función del cociente m/M, con las correspondientes de una cuerda de masa m unida a una partícula de masa M que hemos calculado en el apartado anterior para un valor particular .

kk=logspace(-2,3,100);
w=zeros(1,length(kk));
i=1;
for k=kk
    f=@(x)(bessely(0,2*x*sqrt(1+1/k))*besselj(0,2*x/sqrt(k))-
besselj(0,2*x*sqrt(1+1/k))*bessely(0,2*x/sqrt(k)))*x/sqrt(k)-
bessely(0,2*x*sqrt(1+1/k))*besselj(1,2*x/sqrt(k))+
besselj(0,2*x*sqrt(1+1/k))*bessely(1,2*x/sqrt(k));
    w(i)=fzero(f,1.1);
    i=i+1;
end
y=sqrt((3*kk+6)./(2*kk+6));
semilogx(kk,w,kk,y)
legend('cuerda','varilla','location','northwest')
grid on
xlabel('m/M')
ylabel('\omega/\omega_0')
title('Frecuencias')

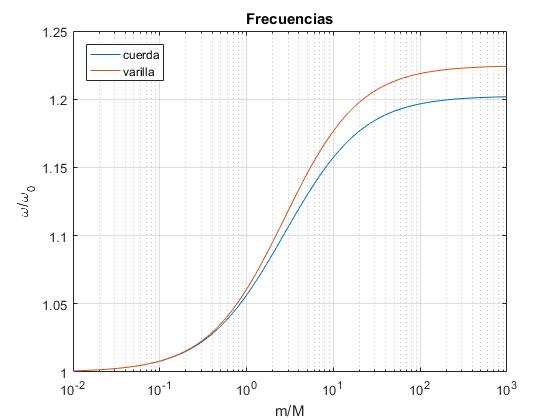
Cuando m/M es pequeño, los dos tipos de péndulos tienen frecuencias parecidas, que empiezan a diferenciarse notablememte a partir de m/M=1

Casos particulares

No hay partícula, M=0

Cuando M=0, no hay partícula, solamente oscila la cuerda

El primer miembro de la ecuación trascendente es cero y ξ₀=0. Si observamos las gráficas de las funciones de Bessel J_n(x) e Y_n(x) veremos que J₀(0)=1, J₁(0)=0, y Y_n(0) tiende a -∞. Para que el segundo miembro de la ecuación trascendente sea cero, J₀(ξ_l) tiene que ser cero, es decir ξ_l tiene que ser una raíz de J₀(x)=0. La primera raíz es 2.4048

>> fzero(@(x) besselj(0,x),2)
ans =    2.4048

2ω/ω₀= 2.4048, ω=1.2024ω₀

La masa de la cuerda es pequeña

Cuando la masa m de la cuerda es pequeña comparada con la masa de la partícula M o bien, M/m>>1

El argumento de las funciones de Bessel J_n(x) e Y_n(x) son grandes y podremos utilizar las aproximaciones

${\displaystyle \{\begin{array}{l}{J}_0(x)\cong \sqrt{\frac{2}{\pi x}}\cos \left(x-\frac{\pi }{4}\right)\\ J_1(x)\cong \sqrt{\frac{2}{\pi x}}\cos \left(x-\frac{3\pi }{4}\right)\end{array}\{\begin{array}{l}{Y}_0(x)\cong \sqrt{\frac{2}{\pi x}}\sin \left(x-\frac{\pi }{4}\right)\\ Y_1(x)\cong \sqrt{\frac{2}{\pi x}}\sin \left(x-\frac{3\pi }{4}\right)\end{array}}$

Después de hacer algunas operaciones la ecuación trascendente se convierte en

${\displaystyle \begin{array}{l}\frac{\omega }{{\omega }_0}\sqrt{\frac{M}{m}}\sin \left({\xi }_l-{\xi }_0\right)=\sin \left({\xi }_l-{\xi }_0+\frac{\pi }{2}\right)\\ \tan \left({\xi }_l-{\xi }_0\right)=\frac{{\omega }_0}{\omega }\sqrt{\frac{m}{M}}\end{array}}$

Ahora bien, cuando m<<M,

${\displaystyle {\xi }_l-{\xi }_0=2\frac{\omega }{{\omega }_0}\sqrt{\frac{M}{m}}\left(\sqrt{\frac{m}{M}+1}-1\right)\simeq 2\frac{\omega }{{\omega }_0}\sqrt{\frac{M}{m}}\left(1+\frac{1}{2}\frac{m}{M}-1\right)=\frac{\omega }{{\omega }_0}\sqrt{\frac{m}{M}}}$

Hemos utilizado la aproximación $\sqrt{1+x}\simeq 1+\frac{1}{2}x+\mathrm{...}$

>> taylor(sqrt(1+x))
 ans =(7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + x/2 + 1

El resultado final es

${\displaystyle \tan \left(\frac{\omega }{{\omega }_0}\sqrt{\frac{m}{M}}\right)=\frac{{\omega }_0}{\omega }\sqrt{\frac{m}{M}}}$

Cuando la cuerda no tiene masa, m tiende a cero tanx≈x, y por tanto ω=ω₀, que es la frecuencia angular del péndulo simple.

Dado el cociente entre la masa de la cuerda y la masa de la partícula, k=m/M, calculamos las raíces de la ecuación trascendente g(x) para obtener la frecuencia angular x=ω/ω₀ de la oscilación del péndulo.

${\displaystyle \tan \left(x\sqrt{k}\right)-\frac{\sqrt{k}}{x}=0}$

En este script representamos la función trascendente f(x) y su aproximación g(x), cuando la masa de la cuerda es pequeña m/M<<1

k=0.1;
g=@(x) tan(x*sqrt(k))-sqrt(k)./x;
f=@(x)(bessely(0,2*x*sqrt(1+1/k)).*besselj(0,2*x/sqrt(k))-
besselj(0,2*x*sqrt(1+1/k)).*bessely(0,2*x/sqrt(k))).*x/sqrt(k)-
bessely(0,2*x*sqrt(1+1/k)).*besselj(1,2*x/sqrt(k))+
besselj(0,2*x*sqrt(1+1/k)).*bessely(1,2*x/sqrt(k));
hold on
fplot(g,[0.1,15])
fplot(f,[0.1,15])
hold off
grid on
legend('aproximada','exacta','location','southeast')
ylim([-1,1])
xlabel('x')
ylabel('f(x)')
title('gráfica de f(x)')

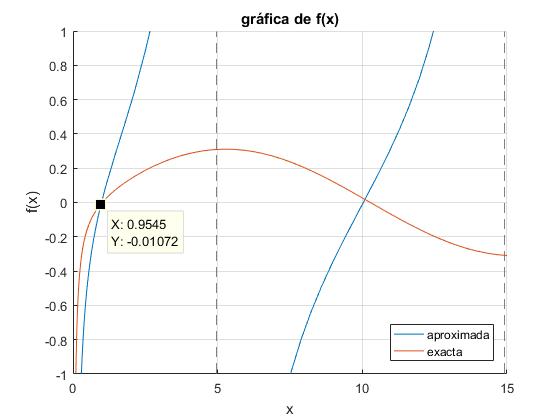
>> fzero(f,1)
ans =    1.0079
>> fzero(g,1)
ans =    0.9836

Las raíces coinciden y son próximas a 1, de modo que cuando la masa de la cuerda es pequeña, ω≈ω₀

Referencias

H. L. Armstrong. Effect of the mass of the cord on the period of a simple pendulum. Am. J. Phys. 44 (6) June 1976, pp. 564-566

J S Deschaine, B H Suits. The hanging cord with a real tip mass. Eur. J.Phys. 29 (2008) pp. 1211-1222