Una partícula desliza en el interior de un aro que rueda
En la figura, se muestra una partícula de masa m en el interior de un aro de masa M y radio R. La posición del centro del aro es x y la posición de la partícula dentro del aro viene dada por el ángulo θ.
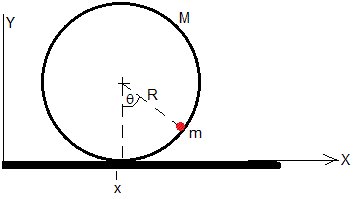
En el instante t, las coordenadas de la partícula son (x+Rsinθ, R-Rcosθ) y las componentes de su velocidad, se obtienen derivando respecto del tiempo.
Energía del sistema
La energía cinética del sistema se compone de dos términos:
Energía cinética del aro de masa M y momento de inercia MR2, que rueda sin deslizar con velocidad v=dx/dt
Energía cinética de la partícula de masa m
La velocidad de traslación del centro de masas es v=dx/dt y la velocidad angular de rotación alrededor del eje del aro es v/R. La energía cinética del aro es la suma de las dos contribuciones (traslación del c.m. y rotación alrededor de un eje que pasa por el c.m.).
La energía potencial del aro no cambia. La energía potencial de la partícula es Ep=mgR(1-cosθ), tomando el plano horizontal como nivel cero.
La energía total E=Ek1+Ek2+Ep del sistema se conserva.
Ecuaciones del movimiento
La lagrangiana L=Ek1+Ek2-Ep
Observamos que la lagrangiana L no depende de x
Una magnitud se mantiene constante
En el instante t=0, el aro está en reposo y la partícula se suelta en el interior del aro en la posición angular θ0, entonces, dx/dt=0 y dθ/dt=0, por lo que la constante es cero
La segunda ecuación del movimiento se obtiene
El resultado es
Derivamos la primera ecuación diferencial respecto del tiempo,
Entre estas dos últimas ecuaciones diferenciales, eliminamos d2x/dt2 y despejamos d2θ/dt2
Tenemos que resolver por procedimientos numéricos, el sistema de dos ecuaciones diferenciales
con las condiciones iniciales siguientes: en el instante t=0, θ=θ0, dθ/dt=0, x=0.
La segunda ecuación, nos relaciona el desplazamiento del centro del aro x y la posición angular de de la partícula θ en el interior del aro
Integramos sabiendo que para θ=θ0, x=0
Por ejemplo, para R=1, m=1, M=2.5. Situamos la partícula en la posición angular θ0=π/3 (60°) y la soltamos, cuando pasa por θ=0, entonces la posición del centro del aro es, x=0.14, tal como podemos apreciar en el programa interactivo, al final de la página
Aproximaciones
Cuando la posición angular de la partícula dentro del aro θ es pequeña hacemos las siguientes aproximaciones, cosθ≈1 y sinθ≈θ, sin2θ≈0, θ·(dθ/dt)2≈0. La primera ecuación diferencial se convierte en
que es la ecuación diferencial de un Movimiento Armónico Simple de frecuencia angular ω y periodo P=2π/ω
La solución de esta ecuación diferencial con las condiciones iniciales especificadas: t=0, θ=θ0, dθ/dt=0, es
θ=θ0cos(ωt)
La segunda ecuación diferencial se escribe
Integramos esta ecuación, con la condición inicial, t=0, x=0
Solución numérica
Consideremos el sistema formado por
- Una partícula de masa m=1
- Un aro de masa, M=2.5 y radio R=1
La partícula se sitúa en la posición angular θ0=π/12 (15°) en el instante inicial t=0. Se representa la posición angular θ de la partícula en el interior del aro en función del tiempo t y la posición del centro del aro x en función del tiempo
m=1; %masa partícula
M=2.5; %masa del aro
R=1; %radio del aro
angulo=pi/12; %posición angular de la partícula
w=sqrt((m+2*M)*9.8/(2*M*R)); %frecuencia angular
tFin=4*pi/w; %dos oscilaciones
%x(2) es vy, x(1) es y,
x0=[angulo,0,0]; %[y, vy, x]
fg=@(t,x) [x(2);(-(m+2*M)*9.8*sin(x(1))/R-m*sin(x(1))*cos(x(1))*x(2)^2)
/(m*sin(x(1))^2+2*M);-m*R*cos(x(1))*x(2)/(m+2*M)];
[t,x]=ode45(fg,[0,tFin],x0);
subplot(2,1,1)
hold on
plot(t, x(:,1))
fplot(@(t) angulo*cos(w*t),[0,tFin])
hold off
xlabel('t')
ylabel('\theta');
grid on
legend('exacto','aproximado','location','south')
title('Posición angular')
subplot(2,1,2)
hold on
plot(t, x(:,3))
fplot(@(t) m*R*angulo*(1-cos(w*t))/(m+2*M),[0,tFin])
hold off
xlabel('t')
ylabel('x');
legend('exacto','aproximado','location','north')
grid on
title('Posición del centro del aro')
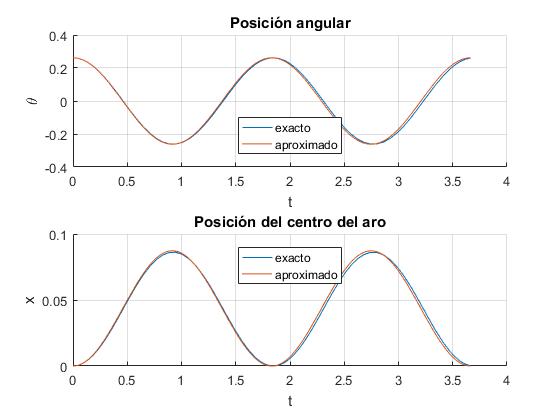
En la representación gráfica, vemos que cuando la posición angular de la partícula θ0 es pequeña, la solución numérica de las ecuaciones del movimiento se ajusta a sus aproximaciones analíticas
Comprobamos el principio de conservación de la energía, la energía inicial es E=mgR(1-cosθ0)
>>m*9.8*R*(1-cos(angulo)) ans = 0.3339
Calculamos la energía en cada instante, la variable vx es dx/dt
>> vx=-m*R*cos(x(:,1)).*x(:,2)/(m+2*M);
>> E=(m+2*M)*vx.^2/2+m*(R*x(:,2)).^2/2+m*R*x(:,2).*vx.*cos(x(:,1))
+m*9.8*R*(1-cos(x(:,1)))
E =
0.3339
0.3339
0.3339
......
0.3336
Periodo
La energía es constante e igual a la energía inicial
La lagrangiana L no depende de la variable x, por tanto, hay otra constante del movimiento
Despejamos dx/dt en la segunda ecuación y sustituimos en la primera. Despejamos dθ/dt
Integramos la variable θ entre 0 y θ0 para obtener un cuarto de periodo
La función integral de MATLAB calcula, empleando procedimientos numéricos, la integral definida
m=1; %masa partícula M=4; %masa del aro R=1; %radio del aro angulo=pi/3; %posición inicial f=@(x) sqrt((m*sin(x).^2+2*M)./(cos(x)-cos(angulo))); P=2*sqrt(2*R/(9.8*(m+2*M)))*integral(f,0, angulo); disp(P)
2.0831
Actividades
Se introduce
- La masa del aro M en el control titulado Masa aro
- La posición angular de la partícula θ0 en el control titulado Angulo inicial
- La masa de la partícula se ha fijado en m=1
- El radio del aro se ha fijado en R=1
Se pulsa el botón titulado Nuevo
Observamos el movimiento de la partícula y del aro. Se proporciona los valores:
- El tiempo t
- La posición del centro del aro x
- La posición angular de la partícula θ en grados, en el interior del aro
El lector puede medir el periodo de la oscilación utilizando los botones Pausa || y Paso a paso >|
El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente
donde E es la energía del sistema en cualquier instante t, y E0 es la energía inicial del sistema.
Este valor se proporciona en caracteres de color rojo en la parte derecha. Su valor debe ser siempre cero, o un valor muy pequeño lo que indica que la energía del sistema permanece constante y el programa realiza los cálculos correctamente.

