Consideremos una partícula de masa m que se mueve en el potencial

${\displaystyle E_p(x)=\{\begin{array}{l}\frac{1}{2}k{\left(x+x_0\right)}^2,x\ge 0\\ \frac{1}{2}k{\left(x-x_0\right)}^2,x<0\end{array}}$

Representamos la energía potencial E_p(x) para x₀=-2 (x₀<0) y k=1

x0=-2;
k=1; 
hold on
fplot(@(x) k*(x+x0).^2/2, [0,5])
fplot(@(x) k*(x-x0).^2/2, [-5,0])
hold off
grid on
xlabel('x')
ylabel('E_p(x)')
title('Energía potencial')

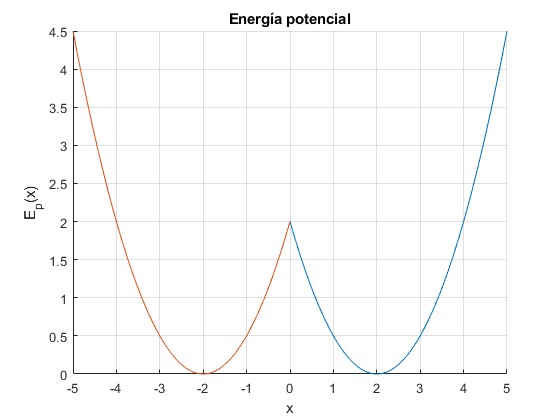
Hay dos mínimos en x=2 y x=-2, separados por un máximo local en x=0. La función E_p(x) es continua en x=0 pero no su derivada

Amplitud y periodo

Representamos la energía potencial E_p(x) para x₀=2 (x₀>0) y k=1

x0=2;
k=1;
E=15; %energía
a=sqrt(2*E/k)-x0; %amplitud
hold on
fplot(@(x) k*(x+x0).^2/2, [0,5])
fplot(@(x) k*(x-x0).^2/2, [-5,0])
line([-a,a],[E,E])
line([a,a],[0,E],'lineStyle','--')
line([-a,-a],[0,E],'lineStyle','--')
hold off
grid on
xlabel('x')
ylabel('E_p(x)')
title('Energía potencial')

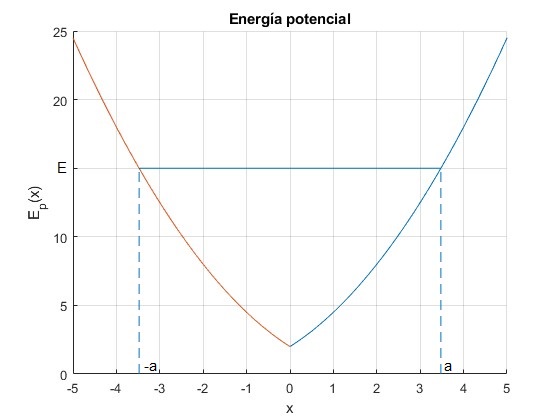
El mínimo de la función E_p(x) está en x=0,

${\displaystyle E_p(0)=\frac{1}{2}k{x}_0^2}$

La función es continua pero no lo es su derivada. Este es el caso (x₀>0), que vamos a estudiar a continuación

Dada la energía E de la partícula calculamos su máximo desplazamiento a, sabiendo que la velocidad de la partícula v=0, para x=a

El principio de conservación de la energía es

${\displaystyle \frac{1}{2}m{v}^2+E_p(x)=E}$

En la posición de máximo desplazamiento x=a

${\displaystyle \begin{array}{l}\frac{1}{2}k{\left(a+x_0\right)}^2=E\\ a=\sqrt{\frac{2E}{k}}-x_0\end{array}}$

>> a
a =    3.4772

Cuando pasa por el mínimo x=0, el módulo de la velocidad de la partícula es

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}^2+\frac{1}{2}k{x}_0^2=E\\ \frac{1}{2}m{v}^2+\frac{1}{2}k{x}_0^2=\frac{1}{2}k{\left(a+x_0\right)}^2\\ v={\omega }_0\sqrt{\left(a^2+2a{x}_0\right)}={\omega }_0\sqrt{a\left(a+2x_0\right)},{\omega }_0^2=\frac{k}{m}\end{array}}$

El periodo P es cuatro veces el tiempo que tarda la partícula en desplazarse de x=0 hasta x=a

${\displaystyle \begin{array}{l}\frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}k{\left(x+x_0\right)}^2=E\\ \frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}k{\left(x+x_0\right)}^2=\frac{1}{2}k{\left(a+x_0\right)}^2\\ dt=\frac{dx}{\sqrt{\frac{k}{m}{\left(a+x_0\right)}^2-\frac{k}{m}{\left(x+x_0\right)}^2}}=\sqrt{\frac{m}{k}}\frac{dx}{\sqrt{-x^2-2x_{0}x+a^2+2a{x}_0}}\\ P=4\sqrt{\frac{m}{k}}{\displaystyle \underset{0}{\overset{a}{\int }}\frac{dx}{\sqrt{-x^2-2bx+c}}},\{\begin{array}{l}b=x_0\\ c=a^2+2a{x}_0\end{array}\end{array}}$

Agrupamos términos bajo la raíz, para obtener una integral inmediata

${\displaystyle {\displaystyle \int \frac{dx}{\sqrt{-x^2-2bx+c}}}={\displaystyle \int \frac{dx}{\sqrt{c+b^2-{\left(x+b\right)}^2}}}}$

Hacemos un cambio de variable

${\displaystyle \begin{array}{l}z=x+b,dz=dx\\ {\displaystyle \int \frac{dz}{\sqrt{c+b^2-z^2}}}=\arcsin \left(\frac{z}{\sqrt{c+b^2}}\right)=\arcsin \left(\frac{x+b}{\sqrt{c+b^2}}\right)=\arcsin \left(\frac{x+x_0}{a+x_0}\right)\end{array}}$

El resultado es el periodo P

${\displaystyle P=4\sqrt{\frac{m}{k}}\left\{\arcsin \left(1\right)-\arcsin \left(\frac{x_0}{a+x_0}\right)\right\}=\frac{4}{{\omega }_0}\left\{\frac{\pi }{2}-\arcsin \left(\frac{x_0}{a+x_0}\right)\right\}}$

Ecuación del movimiento

La fuerza sobre la partícula es

${\displaystyle F=-\frac{d{E}_p}{dx}=\{\begin{array}{l}-k\left(x+x_0\right),x\ge 0\\ -k\left(x-x_0\right),x<0\end{array}}$

Resolveremos las ecuaciones diferenciales del movimiento

• A la derecha del origen, x≥0

${\displaystyle \frac{d^{2}x}{d{t}^2}+{\omega }_0^2\left(x+x_0\right)=\mathrm{0,}x\ge 0}$

La solución particular es una constante C que introducimos en la ecuación diferencial

${\displaystyle \begin{array}{l}{\omega }_0^2\left(C+x_0\right)=0\\ C=-x_0\end{array}}$

La solución completa es la suma de la particular y la homogénea

${\displaystyle \begin{array}{l}x=A_1\cos \left({\omega }_{0}t\right)+B_1\sin \left({\omega }_{0}t\right)-x_0\\ \frac{dx}{dt}={\omega }_0\left(-A_1\sin \left({\omega }_{0}t\right)+B_1\cos \left({\omega }_{0}t\right)\right)\end{array}}$

Las condiciones iniciales (posición inicial y velocidad inicial) determinan los coeficientes A₁ y B₁

• A la izquierda del origen, x<0

${\displaystyle \frac{d^{2}x}{d{t}^2}+{\omega }_0^2\left(x-x_0\right)=\mathrm{0,}x<0}$

La solución particular es una constante C que introducimos en la ecuación diferencial

${\displaystyle \begin{array}{l}{\omega }_0^2\left(C-x_0\right)=0\\ C=x_0\end{array}}$

La solución completa es la suma de la particular y la homogénea

${\displaystyle \begin{array}{l}x=A_2\cos \left({\omega }_{0}t\right)+B_2\sin \left({\omega }_{0}t\right)+x_0\\ \frac{dx}{dt}={\omega }_0\left(-A_2\sin \left({\omega }_{0}t\right)+B_2\cos \left({\omega }_{0}t\right)\right)\end{array}}$

Las condiciones iniciales (posición inicial y velocidad inicial) determinan los coeficientes A₂ y B₂

Etapas del movimiento

1. Primera etapa, de x=a a x=0

En el instante t=0, la partícula se encuentra en x=a, (máximo desplazamiento), en reposo, dx/dt=0



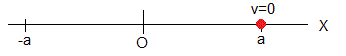
Los coeficientes A₁ y B₁ son

${\displaystyle \{\begin{array}{l}a=A_1-x_0\\ 0={\omega }_0{B}_1\end{array}}$

La solución de la ecuación diferencial para x≥0 es

${\displaystyle \begin{array}{l}x=\left(a+x_0\right)\cos \left({\omega }_{0}t\right)-x_0\\ \frac{dx}{dt}=-{\omega }_0\left(a+x_0\right)\sin \left({\omega }_{0}t\right)\end{array}}$

La partícula llega al origen x=0, en el instante T tal que

${\displaystyle \cos \left({\omega }_{0}T\right)=\frac{x_0}{a+x_0}}$

Por simetría, el periodo es cuatro veces el tiempo T

${\displaystyle P=4T=\frac{4}{{\omega }_0}\arccos \left(\frac{x_0}{a+x_0}\right)}$

La expresión del periodo P no parece el mismo que el obtenido al principio de esta página, sin embargo, el resultado es el mismo

>> x0=2;
>> k=1;
>> E=15; %energía
>> a=sqrt(2*E/k)-x0; %amplitud
>> P1=4*acos(x0/(x0+a))
P1 =    4.7880
>> P2=4*(pi/2-asin(x0/(x0+a)));
P2 =    4.7880

2. Segunda etapa, de x=0 a x=-a



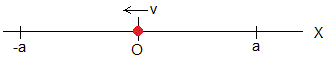
En el instante t=0, la partícula se encuentra en x=0, y su velocidad es

${\displaystyle \frac{dx}{dt}=-{\omega }_0\sqrt{a\left(a+2x_0\right)}}$

Los coeficientes A₂ y B₂ son

${\displaystyle \{\begin{array}{l}0=A_2+x_0\\ -{\omega }_0\sqrt{a\left(a+2x_0\right)}={\omega }_0{B}_2\end{array}}$

La solución de la ecuación diferencial para x<0 es

${\displaystyle \begin{array}{l}x=-x_0\cos \left({\omega }_{0}t\right)-\sqrt{a\left(a+2x_0\right)}\sin \left({\omega }_{0}t\right)+x_0\\ \frac{dx}{dt}={\omega }_0\left(x_0\sin \left({\omega }_{0}t\right)-\sqrt{a\left(a+2x_0\right)}\cos \left({\omega }_{0}t\right)\right)\end{array}}$

La partícula, llega a x=-a en el instante T con velocidad nula

${\displaystyle \begin{array}{l}\{\begin{array}{l}-a=-x_0\cos \left({\omega }_{0}T\right)-\sqrt{a\left(a+2x_0\right)}\sin \left({\omega }_{0}T\right)+x_0\\ 0={\omega }_0\left(x_0\sin \left({\omega }_{0}T\right)-\sqrt{a\left(a+2x_0\right)}\cos \left({\omega }_{0}T\right)\right)\end{array}\\ \sin \left({\omega }_{0}T\right)=\frac{\sqrt{a\left(a+2x_0\right)}}{x_0}\cos \left({\omega }_{0}T\right)\\ -a=-x_0\cos \left({\omega }_{0}T\right)-\frac{a\left(a+2x_0\right)}{x_0}\cos \left({\omega }_{0}T\right)+x_0\\ a+x_0=\frac{x_0^2+a^2+2a{x}_0}{x_0}\cos \left({\omega }_{0}T\right)\\ T=\frac{1}{{\omega }_0}\arccos \left(\frac{x_0}{a+x_0}\right)\end{array}}$

El mismo resultado que hemos obtenido en la primera etapa

3. Tercera etapa, de x=-a a x=0

En el instante t=0, la partícula se encuentra en x=-a, en reposo, dx/dt=0



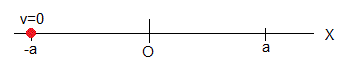
Los coeficientes A₂ y B₂ son

${\displaystyle \begin{array}{l}-a=A_2+x_0\\ 0={\omega }_0{B}_2\end{array}}$

La solución de la ecuación diferencial para x<0 es

${\displaystyle \begin{array}{l}x=-\left(a+x_0\right)\cos \left({\omega }_{0}t\right)+x_0\\ \frac{dx}{dt}={\omega }_0\left(a+x_0\right)\sin \left({\omega }_{0}t\right)\end{array}}$

4. Cuarta etapa, de x=0 a x=a

En el instante t=0, la partícula se encuentra en x=0, y su velocidad es

${\displaystyle \frac{dx}{dt}={\omega }_0\sqrt{a\left(a+2x_0\right)}}$



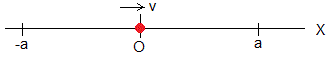
Los coeficientes A₁ y B₁ son

${\displaystyle \begin{array}{l}0=A_1-x_0\\ {\omega }_0\sqrt{a\left(a+2x_0\right)}={\omega }_0{B}_1\end{array}}$

La solución de la ecuación diferencial para x≥0 es

${\displaystyle \begin{array}{l}x=x_0\cos \left({\omega }_{0}t\right)+\sqrt{a\left(a+2x_0\right)}\sin \left({\omega }_{0}t\right)-x_0\\ \frac{dx}{dt}={\omega }_0\left(-x_0\sin \left({\omega }_{0}t\right)+\sqrt{a\left(a+2x_0\right)}\cos \left({\omega }_{0}t\right)\right)\end{array}}$

Hemos obtenido las ecuaciones del movimiento a partir de tiempos parciales, tomando t=0, al principio de cada etapa. Las ecuaciones del movimiento de la partícula tomando t=0, al principio de la primera etapa son

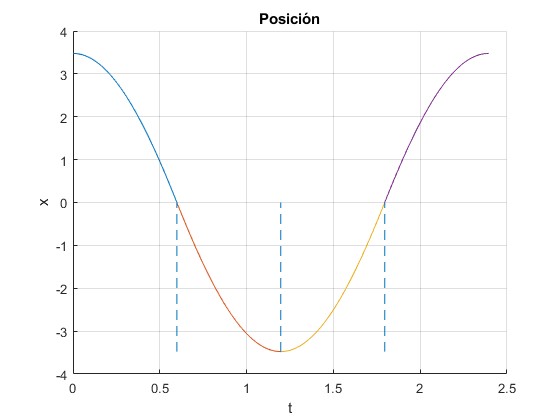
• Posición

${\displaystyle \begin{array}{l}\{\begin{array}{l}{x}_1=\left(a+x_0\right)\cos \left({\omega }_{0}t\right)-x_0,0\le t<T\\ x_2=-x_0\cos \left({\omega }_0\left(t-T\right)\right)-\sqrt{a\left(a+2x_0\right)}\sin \left({\omega }_0\left(t-T\right)\right)+x_0,T\le t<2T\\ x_3=-\left(a+x_0\right)\cos \left({\omega }_0\left(t-2T\right)\right)+x_0,2T\le t<3T\\ x_4=x_0\cos \left({\omega }_0\left(t-3T\right)\right)+\sqrt{a\left(a+2x_0\right)}\sin \left({\omega }_0\left(t-3T\right)\right)-x_0,3T\le t<P\end{array}\\ T=\frac{1}{{\omega }_0}\arccos \left(\frac{x_0}{a+x_0}\right)\end{array}}$

T es el tiempo que emplea la partícula en cada etapa y P=4T es el periodo

Representamos la posición de la partícula en función del tiempo durante un periodo P, con los siguientes datos:

• Desplazamiento, x₀=2
• Constante, k=1
• Energía de la partícula, E=15
• Frecuencia angular, ω₀=2

x0=2;
k=1;
E=15; %energía
a=sqrt(2*E/k)-x0; %amplitud
w0=2;%frecuencia angular, sqrt(k/m)
T=acos(x0/(a+x0))/w0;
hold on
x1=@(t) (a+x0)*cos(w0*t)-x0;
fplot(x1,[0,T])
x2=@(t) -x0*cos(w0*(t-T))-sqrt(a*(a+2*x0))*sin(w0*(t-T))+x0;
fplot(x2,[T,2*T])
x3=@(t) -(a+x0)*cos(w0*(t-2*T))+x0;
fplot(x3,[2*T,3*T])
x4=@(t) x0*cos(w0*(t-3*T))+sqrt(a*(a+2*x0))*sin(w0*(t-3*T))-x0;
fplot(x4,[3*T,4*T])

line([T,T],[-a,0],'lineStyle','--')
line([2*T,2*T],[-a,0],'lineStyle','--')
line([3*T,3*T],[-a,0],'lineStyle','--')
hold off
grid on
xlabel('t')
ylabel('x')
title('Posición')



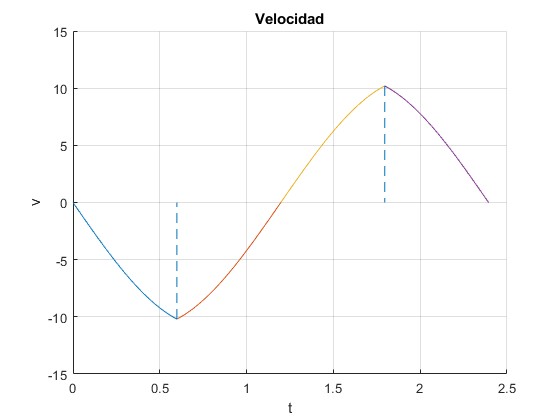
• Velocidad

${\displaystyle \{\begin{array}{l}\frac{d{x}_1}{dt}=-{\omega }_0\left(a+x_0\right)\sin \left({\omega }_{0}t\right),0\le t<T\\ \frac{d{x}_2}{dt}={\omega }_0\left(x_0\sin \left({\omega }_0\left(t-T\right)\right)-\sqrt{a\left(a+2x_0\right)}\cos \left({\omega }_0\left(t-T\right)\right)\right),T\le t<2T\\ \frac{d{x}_3}{dt}={\omega }_0\left(a+x_0\right)\sin \left({\omega }_0\left(t-2T\right)\right),2T\le t<3T\\ \frac{d{x}_4}{dt}={\omega }_0\left(-x_0\sin \left({\omega }_0\left(t-3T\right)\right)+\sqrt{a\left(a+2x_0\right)}\cos \left({\omega }_0\left(t-3T\right)\right)\right),3T\le t<P\end{array}}$

Representamos la velocidad de la partícula en función del tiempo durante un periodo P, con los mismos datos

x0=2;
k=1;
E=15; %energía
a=sqrt(2*E/k)-x0; %amplitud
w0=2;%frecuencia angular, sqrt(k/m)
T=acos(x0/(a+x0))/w0;
hold on
v1=@(t) -w0*(a+x0)*sin(w0*t);
fplot(v1,[0,T])
v2=@(t) w0*(x0*sin(w0*(t-T))-sqrt(a*(a+2*x0))*cos(w0*(t-T)));
fplot(v2,[T,2*T])
v3=@(t) w0*(a+x0)*sin(w0*(t-2*T));
fplot(v3,[2*T,3*T])
v4=@(t) w0*(-x0*sin(w0*(t-3*T))+sqrt(a*(a+2*x0))*cos(w0*(t-3*T)));
fplot(v4,[3*T,4*T])

line([T,T],[v1(T),0],'lineStyle','--')
line([3*T,3*T],[v3(3*T),0],'lineStyle','--')
hold off
grid on
xlabel('t')
ylabel('v')
title('Velocidad')

Referencias

John S. Thomsen. A benevolent nonlinear system: The dynamically shifted oscillator. Am. J. Phys. 56 (2) February 1988, pp. 123-128