Para realizar el experimento, se precisa de un globo lleno de helio de cualquier tamaño, una habitación libre de corrientes de aire, en la que se ha establecido un gradiente de temperaturas entre el suelo y el techo de alrededor de 2ºC/m.

La ecuación de los gases perfectos nos permite relacionar la densidad y la temperatura

pV=nRT,

donde n es el número de moles n=m/M , el cociente entre la masa m del gas y el peso molecular M, p es la presión en Pa, R=8.3143 J/(K·mol) es la constante de los gases, y T es la temperatura absoluta.

${\displaystyle \rho =\frac{m}{V}=\frac{pM}{RT}}$

Una situación análoga son las oscilaciones que experimenta un cuerpo en una solución salina estratificada.

Oscilaciones cuando la temperatura es constante y la presión varía con la altura

Vamos analizar primero el caso más simple, aquél en el que la presión cambia con la altura en un recinto que contiene aire a la misma temperatura T₀.

La ecuación fundamental de la hidrostática que nos da la variación de la presión con la altura dp=-ρg·dz, junto con la ecuación de los gases ideales conduce a

${\displaystyle {\displaystyle \underset{{\rho }_0}{\overset{\rho }{\int }}\frac{d\rho }{\rho }}=-{\displaystyle \underset{0}{\overset{z}{\int }}\frac{Mg}{RT}dz}\rho ={\rho }_0\exp \left(-\frac{Mg}{RT}z\right)}$

La presión p y la densidad ρ disminuyen exponencialmente con la altura z en una atmósfera isoterma.

Si se suelta un globo, flotará en una posición de equilibrio z₀ tal que el peso se equilibra con el empuje.

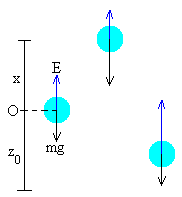
• Si el globo se desplaza x>0  de la posición de equilibrio, la densidad del aire disminuye, el empuje disminuye y la fuerza resultante tratará de retornar el globo a la posición de equilibrio estable.
• Si se desplaza x<0 de la posición de equilibrio, la densidad del aire aumenta, el empuje aumenta y la fuerza resultante tratará de retornar el globo a la posición de equilibrio estable.

La fuerza neta sobre el globo es de sentido contrario al desplazamiento, siendo nula en la posición de equilibrio, un signo inequívoco de que el globo describe una oscilación. Para que sea un Movimiento Armónico Simple, la fuerza resultante F debe de ser proporcional al desplazamiento x.

Llamando ahora ρ₀ a la densidad del aire en la posición de equilibrio z₀, y ρ a la densidad del aire en la posición z₀+x que ocupa el globo. La fuerza neta sobre el globo de masa m será el empuje menos el peso

F= ρgV-mg=(ρ-ρ₀)gV

La segunda ley de Newton se escribe

ma=(ρ-ρ₀)gV

en forma de ecuación diferencial

${\displaystyle \frac{d^{2}x}{d{t}^2}+\frac{{\rho }_0-\rho }{{\rho }_0}g=0}$

Para pequeños desplazamientos x, la función exponencial decreciente, se escribe

${\displaystyle \frac{\Delta \rho }{{\rho }_0}=-\frac{Mg}{R{T}_0}x}$

Tenemos ahora una ecuación diferencial más simple.

${\displaystyle \frac{d^{2}x}{d{t}^2}+\frac{M{g}^2}{R{T}_0}x=0}$

El globo describe un M.A.S. cuya frecuencia angular ω₀ es

${\displaystyle {\omega }_0^2=\frac{M{g}^2}{R{T}_0}P=\frac{2\pi }{{\omega }_0}}$

Para el aire M=0.0289 kg, g=9.8 m/s², y R=8.3143 J/(K·mol) y a la temperatura ambiente T₀=20ºC =293 K, el periodo de la oscilación es P=186 s.

Oscilaciones cuando se establece un gradiente de temperatura

Sea T_a la temperatura en el suelo de una habitación de altura h y T_b la temperatura en el techo. Suponiendo una variación lineal de la temperatura con la altitud, la temperatura T a una altura z, es 

${\displaystyle T=T_a+\frac{T_b-T_a}{h}z}$

La pendiente de la recta (T_b-T_a)/h es el gradiente de temperatura, que supondremos positivo (la temperatura del techo es mayor que la del suelo).

La situación de equilibrio se establece a aquella altura z₀ en la que el peso del globo mg se iguala al empuje ρ₀gV. Siendo m la masa del globo y V su volumen, ρ₀ la densidad del aire en dicha posición y T₀=pM/(R·ρ₀) la correspondiente temperatura.

mg=ρ₀gV

Desplazamos el globo desde la posición de equilibrio z₀, a la posición z₀+x.

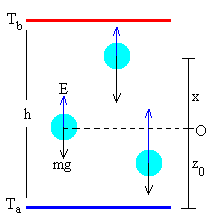
• Si x>0 la temperatura aumenta, densidad del aire disminuye, el peso es mayor que el empuje, la fuerza resultante tiende a retornar el globo hacia la posición de equilibrio.
• Si x<0 la temperatura disminuye, densidad del aire aumenta, el peso es menor que el empuje, la fuerza resultante tiende a retornar el globo hacia la posición de equilibrio.

La fuerza resultante F sobre el globo es de sentido contrario al desplazamiento, siendo nula en la posición de equilibrio, un signo inequívoco de que el globo describe una oscilación. Para que sea un Movimiento Armónico Simple, la fuerza  resultante F debe de ser proporcional al desplazamiento x.

F= ρgV-mg=(ρ-ρ₀)gV

La segunda ley de Newton se escribe

ma=(ρ-ρ₀)gV

en forma de ecuación diferencial

${\displaystyle \frac{d^{2}x}{d{t}^2}+\frac{{\rho }_0-\rho }{{\rho }_0}g=0}$

Calculamos la temperatura T en la posición z₀+x

${\displaystyle T=T_0+\frac{T_b-T_a}{h}x}$

y la variación relativa de la densidad ρ del aire

${\displaystyle \frac{{\rho }_0-\rho }{{\rho }_0}=\left(\frac{T_b-T_a}{h}x\right)\left(\frac{1}{T_0+\frac{T_b-T_a}{h}x}\right)}$

Si la amplitud de la oscilación no es muy grande aproximamos el segundo término entre paréntesis por 1/T₀. Quedando la ecuación diferencial de forma más simple

${\displaystyle \frac{d^{2}x}{d{t}^2}+\left(\frac{T_b-T_a}{h}\right)\frac{g}{T_0}x=0}$

La frecuencia angular del M.A.S. es

${\displaystyle {\omega }_0^2=\left(\frac{T_b-T_a}{h}\right)\frac{g}{T_0}}$

Depende del gradiente de temperatura y del valor de la temperatura en la posición de equilibrio.

La solución de la ecuación diferencial es

x=Asin(ω₀t+φ)

Donde la amplitud A y la fase inicial φ se determinan a partir de las condiciones iniciales, que supondremos, por simplicidad las siguientes: en el instante t=0, x=A, v=dx/dt=0.

La solución de la ecuación diferencial con las condiciones iniciales especificadas es:

x=Asin(ω₀t+π/2)= Acos(ω₀t)

Una deducción alternativa más breve es la siguiente

Si la densidad es inversamente proporcional a la temperatura ρ=pM/(RT). El cambio en la densidad suponiendo que la presión p es constante

${\displaystyle \Delta \rho =\rho -{\rho }_0={\left(\frac{d\rho }{dT}\right)}_0\Delta T=-{\rho }_0\frac{\Delta T}{T_0}\Delta T={\left(\frac{dT}{dx}\right)}_{0}x}$

Llegando a una expresión similar para la frecuencia angular

${\displaystyle {\omega }_0^2=\left(\frac{dT}{dx}\right)\frac{g}{T_0}P=\frac{2\pi }{{\omega }_0}}$

El término entre paréntesis, es el gradiente de temperatura (T_b-T_a)/h, suponiendo una variación lineal de la temperatura con la altura.

Por ejemplo, un gradiente de temperatura de 2ºC/m, estando la posición de equilibrio a la temperatura ambiente de T₀=20ºC=293 K, produce una oscilación cuyo periodo es de P=25 s.

En general, cuando se estudia el fenómeno de la oscilación de un globo habrá que tener en cuenta la variación de la densidad debido a los gradientes de temperatura y también, a los cambios de altura. Estos últimos, pueden considerarse despreciables frente a los primeros para gradientes de temperatura superiores a 1ºC/m.

Oscilaciones amortiguadas

Si suponemos que el globo se mueve en el aire en régimen laminar, es aplicable la ley de Stokes. La fuerza de rozamiento es proporcional a la velocidad, el globo describe una oscilación amortiguada

F_r=6πRηv

Siendo R el radio del globo, y η=1.8·10^-5 Ns/m² la viscosidad del aire.

La amplitud de la oscilación decrece exponencialmente con el tiempo A·exp(-γt)

${\displaystyle 2\gamma =\frac{6\pi R\eta }{{\rho }_0\frac{4}{3}\pi R^3}}$

La densidad del globo es igual a la del aire en la posición de equilibrio ρ₀ ≈1.2 kg/m³. Para un globo de R=15 cm de radio γ=1.5·10^-3 s^-1. La amplitud se reduce en 1/e al cabo de un tiempo de 666.7 s. Así pues, el rozamiento con el aire tiene un efecto pequeño en el periodo de las oscilaciones del globo, ya que el tiempo que tarda la oscilación en reducir su amplitud de forma significativa es grande comparado con el periodo de las oscilaciones libres del globo.

Actividades

Se introduce

• La temperatura en ºC del suelo de la habitación T_a, en el control titulado Temperatura suelo
• La temperatura en ºC del techo de la habitación T_b, en el control titulado Temperatura techo.
• La altura de la habitación se ha fijado en el programa interactivo en el valor h=2.5 m

Se pulsa el botón titulado Nuevo

Observamos la oscilación de un globo de 15 cm de radio. Por conveniencia, se ha supuesto que las características del globo son tales que posición de equilibrio se produce a la mitad de la altura de la habitación cuya temperatura es

${\displaystyle T_0=\frac{T_a+T_b}{2}}$

• Con los termómetros situados en el suelo T_a y en el techo T_b determinamos el gradiente de temperatura conocida la altura de la habitación h=2.5 m

• El termómetro situado al la mitad de la altura nos mide la temperatura T₀ para de la posición de equilibrio del globo.

A partir de estos datos, calculamos el periodo P de oscilación del globo y lo comparamos con las medidas que tomamos en la simulación.

Referencias

Mellen W. Oscillation of a gas balloon due to a temperature gradient. Am. J. Phys. 58 (8) August 1990, pp. 781-782