Oscilaciones de una placa horizontal apoyada en dos rodillos que giran
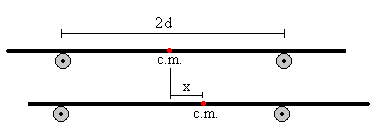
Supongamos que el c.m. de la placa se desplaza x de la posición de equilibrio, hacia la derecha. Dibujamos las fuerzas que actúan sobre la placa y aplicamos las condiciones de equilibrio
-
Equilibrio de las fueras en la dirección vertical
-
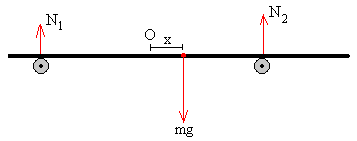
El momento total respecto del cualquier punto debe ser cero. Si elegimos el punto de contacto de la placa con el rodillo derecho, como origen.
N1+N2=mg
donde N1 es la fuerza que ejerce el rodillo izquierdo y N2 es la fuerza que ejerce el rodillo derecho sobre la placa.
-N1·2d+mg·(d-x)=0
Despejamos N1 y N2 en este sistema de dos ecuaciones
Las fuerzas de rozamiento
Las fuerzas de rozamiento en el punto de contacto de los rodillos y la placa son f1=μ·N1 y f2=μ·N2 y sus direcciones son las del movimiento de las ruedas.
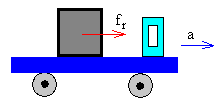
Para entender mejor el sentido de estas dos fuerzas, nos fijaremos que cuando un camión, que trasporta una caja de masa m sobre la plataforma, arranca, la fuerza de rozamiento fr=ma entre la caja y la plataforma hace que la caja permanezca en reposo sobre la plataforma, siempre que se cumpla que fr< μs·N.
Cuando la aceleración a del camión es tal que fr alcanza el valor máximo μs·N, la caja empieza a deslizar sobre la plataforma. La fuerza de rozamiento vale fr= μk·N. La aceleración del camión es a y la aceleración de la caja es ac=fr/m= μk·g. La aceleración de la caja respecto del conductor del camión es ac-a.
Ecuaciones del movimiento de la placa
Examinamos los distintos casos que pueden producirse.
-
Las dos ruedas giran hacia dentro.
-
Las ruedas giran hacia fuera
-
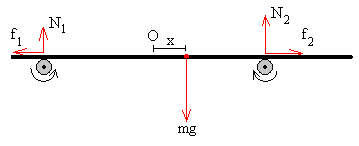
Las ruedas giran en el mismo sentido, por ejemplo, hacia la derecha.
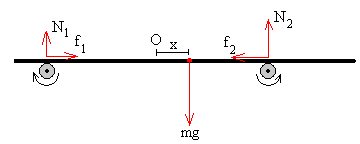
Las fuerzas de rozamiento f1 y f2 tienen los sentidos indicados en la figura. La fuerza horizontal que actúa sobre la placa es
f=f1-f2= μ·N1- μ·N2=-(μmg/d)·x
La fuerza f que actúa sobre la placa es proporcional a su desplazamiento x y de sentido contrario a éste. La ecuación diferencial del movimiento es
La placa describe un MAS de frecuencia angular ω2=μg/d, y de periodo P
La solución de esta ecuación diferencial es
x=A·sin(ωt+φ)
La amplitud A y la fase inicial φ se determinan a partir de las condiciones iniciales.
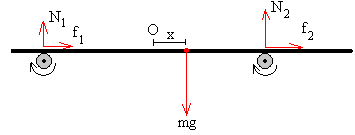
Las fuerzas de rozamiento f1 y f2 tienen los sentidos indicados en la figura. La fuerza horizontal que actúa sobre la placa es
f=f2-f1= μ·N2- μ·N1=(μmg/d)·x
La fuerza f que actúa sobre la placa es proporcional a su desplazamiento x, pero del mismo de sentido. La ecuación diferencial del movimiento es
Esta no es la ecuación de un MAS. La solución de esta ecuación diferencial es
x=A·exp(ωt)+B·exp(-ωt)
donde A y B se determinan a partir de las condiciones iniciales
Las fuerzas de rozamiento f1 y f2 tienen los sentidos indicados en la figura. La fuerza horizontal que actúa sobre la placa es
f=f2+f1= μ·N2+ μ·N1=μmg
La fuerza f es constante, la aceleración de la placa es constante, su movimiento es uniformemente acelerado
La solución es
x=x0+v0·t+μgt2/2
donde x0 y v0 son la posición y la velocidad en el instante t=0.
Ejemplos
d=40 cm
μ=0.8
-
Las ruedas giran en sentido contrario hacia dentro
-
Las ruedas giran en sentido contrario hacia fuera
-
Las ruedas giran en el mismo sentido
El periodo de las oscilaciones es
La amplitud se ha tomado igual a A=10 cm y la fase inicial φ=0. La posición del c.m. es
x=10·sin(4.43·t) cm
La velocidad es
v=dx/dt=A·ω·cos(ωt+φ)
En el instante inicial t=0, la posición inicial es x0=0 y la velocidad inicial es v0=10·4.43=44.3 cm/s
x=A·exp(ωt)+B·exp(-ωt)
v=dx/dt= A·ω·exp(ωt)-B·ω·exp(-ωt)
La naturaleza del movimiento depende de las condiciones iniciales.
Si las condiciones iniciales son tales que A=0, la placa tiende a la posición de equilibrio x=0, después de un tiempo teóricamente infinito. En el caso de que A no sea cero, x se incrementa con el tiempo sin límite, o mejor dicho, hasta que el borde de la placa alcanza a una de las ruedas o el c.m. de la placa sale fuera de la región comprendida entre las ruedas. En este último caso, la posición x=0, es de equilibrio inestable.
En la simulación, las condiciones iniciales se han elegido de modo que A=0.
Para t=0, x0=B, v0=-B·ω
La posición del c.m. en función del tiempo es
En la simulación, las condiciones iniciales, se han elegido de modo que para t=0, x0=0, v0=0, por lo que
El movimiento se detiene cuando el borde de la placa alcanza a una de las ruedas o el c.m. de la placa sale fuera de la región comprendida entre las ruedas.
Actividades
-
Se establece la distancia 2d entre las dos ruedas en el control titulado Posición.
-
El coeficiente de rozamiento μ, en el control titulado Coeficiente de rozamiento
Se elige el sentido del movimiento de las dos ruedas, activando una de las tres casillas
- Girando en sentido contrario, hacia dentro
- Girando en sentido contrario, hacia fuera
- Girando en el mismo sentido
Se pulsa el botón titulado Nuevo.
Se observa el movimiento de la placa.
Oscilaciones. Retención-deslizamiento
Cuando el centro de masas se ha desplazado x, hemos calculado las fuerzas sobre la placa de masa m.
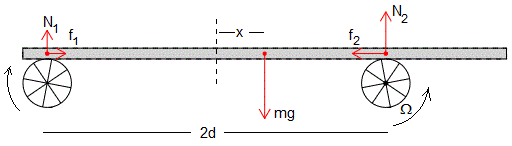
La ecuación del movimiento es
Que es un movimiento armónico simple con frecuencia angular
La solución de esta ecuación diferencial es
donde los coeficientes A y B se determinan a partir de las condiciones iniciales: En el instante t=0, el centro de masas parte de x0 en reposo.
Los rodillos de radio r se mueven con velocidad angular constante Ω. La velocidad relativa de la placa respecto del rodillo derecho es
La velocidad relativa de la placa respecto del rodillo izquierdo es
Pueden ocurrir dos casos
Si Ωr es mayor que la velocidad máxima de la placa ωx0, la velocidad relativa no es nula en ningún instante. La placa oscila con frecuencia angular ω. Tal como se ha estudiado al principio del primer apartado
En cambio, si Ωr<ωx0, en el instante t1 la placa estará en reposo relativo al rodillo derecho. Que es la situación que se va a estudiar en este apartado
en la posición
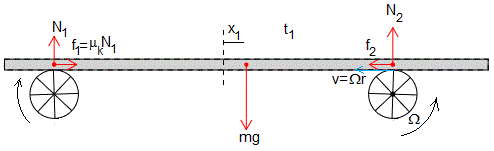
La fuerzas que ejercen los rodillos sobre la placa serán f2 y f1
La placa (en reposo relativo al rodillo derecho) se mueve con velocidad constante Ωr, por lo que f2=f1
Cuando la posición x de el c.m. se hace negativa (al la izquierda del origen) f1 y por tanto, f2 van aumentando y N2 disminuyendo, llegará un momento en que f2 se iguala al valor de la fuerza de rozamiento máxima (μsN2), en la posición x2 tal que
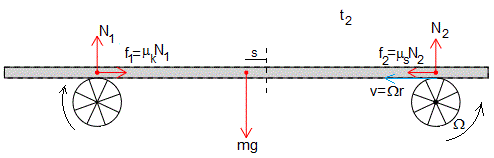
Hemos supuesto que el coeficiente estático μs es mayor que el cinético μk
Entre la posición x1 y x2 el centro de masas se mueve con velocidad constante Ωr
A partir de este instante, la placa oscila, la posición y velocidad del c.m. de la placa son.
donde los coeficientes A y B se determinan a partir de las condiciones iniciales, en el instante t2 la posición del c.m. de la placa es -s y su velocidad -Ωr
La posición del c.m. de la placa para t≥t2 es
La velocidad se hace cero en el instante t1/2 (máximo desplazamiento)
A partir de este instante, la placa se mueve hacia la derecha.
La velocidad relativa de la placa respecto del rodillo izquierdo es
La velocidad relativa de la placa respecto del rodillo derecho es
En el instante t3 la placa está en reposo relativo v=0, respecto del rodillo izquierdo
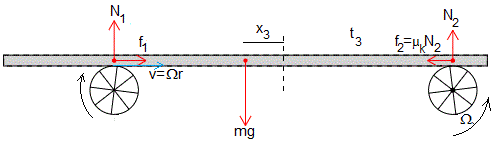
La posición x3 en dicho instante es
Se ha utilizado la relación trigonométrica,
Cuando la posición x de el c.m. se hace positiva (a la derecha del origen) f2 y por tanto, f1 van aumentando y N1 disminuyendo, llegará un momento en que f1 se iguala al valor de la fuerza de rozamiento máxima (μsN1), en la posición x4 tal que
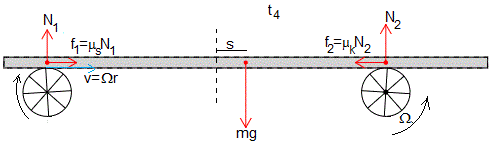
La placa se mueve con velocidad constante Ωr entre las posiciones x3 y x4. Alcanza esta última posición en el instante
A partir de este instante, la placa oscila, la posición y velocidad del c.m. de la placa son
Donde los coeficientes A y B se determinan a partir de las condiciones iniciales: en el instante t4 la posición del c.m. de la placa es s y su velocidad Ωr
La posición del c.m. de la placa para t≥t4 es
La velocidad se anula cuando el desplazamiento es máximo, en el instante T
x0 es la nueva posición de partida y T es el tiempo que tarda en dar una oscilación. A partir de este instante, la placa se mueve hacia la izquierda, repitiéndose el ciclo
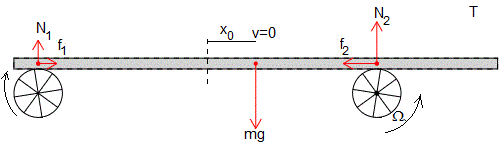
Ejemplo
- Distancia entre los rodillos, 2d=0.6 m
- Velocidad del rodillo (punto de periferia), Ωr=0.3 m/s
- Coeficiente cinético, μk=0.6
- Coeficiente estático, μs=0.7
- Masa de la placa, m= 1 kg
- Posición inicial del centro de masas de la placa, x0=0.15 m
Frecuencia angular
Se cumple que Ωr<ωx0=0.6641 m/s.
Representamos la posición x del centro de masa en función del tiempo t durante la primera oscilación
mu_k=0.6; %coeficiente cinético
mu_s=0.7; %coeficiente estático
d=0.3; %2d distancia entre ruedas
m=1; %masa
om_r=0.3; %velocidad angular*radio
w=sqrt(mu_k*9.8/d); %frecuencia angular
hold on
x0=0.15; %posición inicial del c.m.
x1=sqrt(x0^2-(om_r/w)^2);
t1=asin(om_r/(x0*w))/w;
f=@(t) x0*cos(w*t);
fplot(f,[0,t1]) %posición
line([t1, t1],[0, f(t1)],'lineStyle','--')
s=(mu_s-mu_k)/(mu_s+mu_k);
t2=t1+(s+x1)/om_r;
f=@(t) x0*cos(w*t1)-om_r*(t-t1);
fplot(f,[t1,t2]) %posición
line([t2, t2],[0, f(t2)],'lineStyle','--')
t3=t2+2*atan(om_r/(w*s))/w;
fi=pi-atan(om_r/(w*s));
C=sqrt(s^2+(om_r/w)^2); %amplitud
f=@(t) C*cos(w*(t-t2)+fi);
fplot(f,[t2,t3]) %posición
line([t3, t3],[0, f(t3)],'lineStyle','--')
x3=-s;
t4=t3+2*s/om_r;
f=@(t) x3+om_r*(t-t3);
fplot(f,[t3,t4]) %posición
line([t4, t4],[0, f(t4)],'lineStyle','--')
t5=t4+atan(om_r/(w*s))/w; %periodo
fi=-atan(om_r/(w*s));
f=@(t) C*cos(w*(t-t4)+fi);
fplot(f,[t4,t5]) %posición
line([t5, t5],[0, f(t5)],'lineStyle','--')
hold off
xlabel('t (s)')
ylabel('x (m)')
grid on
title('Posición')
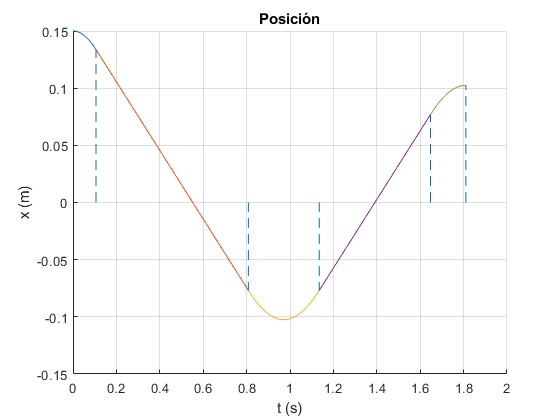
>> t5 t5 = 1.8105 >> f(t5) ans = 0.1025
La posición final x5=0.1025 m, que se alcanza en el instante t5=1.8105 s, es más pequeña que la inicial
Representamos la velocidad v=dx/dt del centro de masa en función del tiempo t durante la primera oscilación
mu_k=0.6; %coeficiente cinético
mu_s=0.7; %coeficiente estático
d=0.3; %2d distancia entre ruedas
m=1; %masa
om_r=0.3; %velocidad angular*radio
w=sqrt(mu_k*9.8/d); %frecuencia angular
hold on
x0=0.15; %posición inicial del c.m.
x1=sqrt(x0^2-(om_r/w)^2);
t1=asin(om_r/(x0*w))/w;
f=@(t) -w*x0*sin(w*t);
fplot(f,[0,t1])
line([t1, t1],[0, f(t1)],'lineStyle','--')
s=(mu_s-mu_k)/(mu_s+mu_k);
t2=t1+(s+x1)/om_r;
line([t2, t2],[0, -om_r],'lineStyle','--')
line([t1,t2],[-om_r, -om_r]) %velocidad
t3=t2+2*atan(om_r/(w*s))/w;
fi=pi-atan(om_r/(w*s));
C=sqrt(s^2+(om_r/w)^2); %amplitud
f=@(t) -w*C*sin(w*(t-t2)+fi);
fplot(f,[t2,t3])
line([t3, t3],[0, f(t3)],'lineStyle','--')
t4=t3+2*s/om_r;
line([t3,t4],[om_r, om_r]) %velocidad
line([t4, t4],[0, om_r],'lineStyle','--')
t5=t4+atan(om_r/(w*s))/w; %periodo
fi=-atan(om_r/(w*s));
f=@(t) -w*C*sin(w*(t-t4)+fi);
fplot(f,[t4,t5])
hold off
xlabel('t (s)')
ylabel('v (m/s)')
grid on
title('Velocidad')
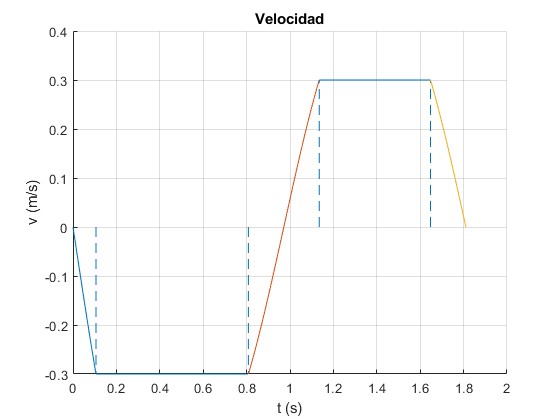
Representamos la velocidad v=dx/dt en función de la posición x del centro de masa durante tres oscilaciones
mu_k=0.6; %coeficiente cinético
mu_s=0.7; %coeficiente estático
d=0.3; %2d distancia entre ruedas
m=1; %masa
om_r=0.3; %velocidad angular*radio
w=sqrt(mu_k*9.8/d); %frecuencia angular
hold on
colores=['r','b','k'];
x5=0.15; %posición inicial
for n=1:3
x0=x5; %posición inicial del c.m.
x1=sqrt(x0^2-(om_r/w)^2);
t1=asin(om_r/(x0*w))/w;
fplot(@(t) x0*cos(w*t), @(t) -w*x0*sin(w*t), [0,t1],
'color',colores(n))
s=(mu_s-mu_k)/(mu_s+mu_k);
t2=t1+(s+x1)/om_r;
fplot(@(t) x0*cos(w*t1)-om_r*(t-t1), @(t) -om_r+0*t, [t1,t2],
'color',colores(n))
t3=t2+2*atan(om_r/(w*s))/w;
fi=pi-atan(om_r/(w*s));
C=sqrt(s^2+(om_r/w)^2); %amplitud
fplot(@(t) C*cos(w*(t-t2)+fi), @(t) -w*C*sin(w*(t-t2)+fi), [t2,t3],
'color',colores(n))
x3=-s;
t4=t3+2*s/om_r;
fplot(@(t) x3+om_r*(t-t3), @(t) om_r+0*t, [t3,t4],'color',colores(n))
t5=t4+atan(om_r/(w*s))/w; %periodo
fi=-atan(om_r/(w*s));
fplot(@(t) C*cos(w*(t-t4)+fi), @(t) -w*C*sin(w*(t-t4)+fi), [t4,t5],
'color',colores(n))
x5=C*cos(w*(t5-t4)+fi); %posición final
v5=-w*C*sin(w*(t5-t4)+fi);
end
hold off
xlabel('x (m)')
ylabel('v (m/s)')
grid on
title('Posición, velocidad')
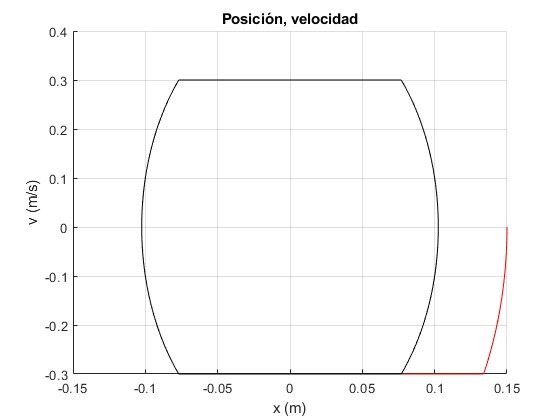
Excepto la primera oscilación (color rojo), las restantes describen la trayectoria (en el espacio de las fases) señalada por las líneas de color negro
Representamos la posición x del centro de masa en función del tiempo t durante las dos primeras oscilaciones
mu_k=0.6; %coeficiente cinético
mu_s=0.7; %coeficiente estático
d=0.3; %2d distancia entre ruedas
m=1; %masa
om_r=0.3; %velocidad angular*radio
w=sqrt(mu_k*9.8/d); %frecuencia angular
x5=0.15;
T=0;
hold on
for n=1:2
x0=x5; %posición inicial del c.m.
x1=sqrt(x0^2-(om_r/w)^2);
t1=asin(om_r/(x0*w))/w;
f=@(t) x0*cos(w*t);
h=fplot(f,[0,t1]);
h.Visible=false;
plot(h.XData+T, h.YData)
line([t1+T, t1+T],[0, f(t1)],'lineStyle','--')
s=(mu_s-mu_k)/(mu_s+mu_k);
t2=t1+(s+x1)/om_r;
f=@(t) x0*cos(w*t1)-om_r*(t-t1);
h=fplot(f,[t1,t2]);
h.Visible=false;
plot(h.XData+T, h.YData)
line([t2+T, t2+T],[0, f(t2)],'lineStyle','--')
t3=t2+2*atan(om_r/(w*s))/w;
fi=pi-atan(om_r/(w*s));
C=sqrt(s^2+(om_r/w)^2); %amplitud
f=@(t) C*cos(w*(t-t2)+fi);
h=fplot(f,[t2,t3]);
h.Visible=false;
plot(h.XData+T, h.YData)
line([t3+T, t3+T],[0, f(t3)],'lineStyle','--')
x3=-s;
t4=t3+2*s/om_r;
f=@(t) x3+om_r*(t-t3);
h=fplot(f,[t3,t4]);
h.Visible=false;
plot(h.XData+T, h.YData)
line([t4+T, t4+T],[0, f(t4)],'lineStyle','--')
t5=t4+atan(om_r/(w*s))/w; %periodo
fi=-atan(om_r/(w*s));
f=@(t) C*cos(w*(t-t4)+fi);
h=fplot(f,[t4,t5]);
h.Visible=false;
plot(h.XData+T, h.YData)
line([t5+T, t5+T],[0, f(t5)],'lineStyle','--')
x5=f(t5);
T=T+t5;
end
hold off
xlabel('t (s)')
ylabel('x (m)')
grid on
title('Posición')
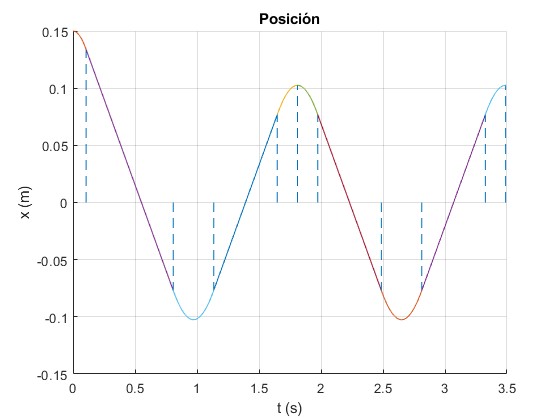
Representamos la velocidad v=dx/dt en función de la posición x del centro de masa durante dos oscilaciones.
Cambiamos la posición inicial x0=0.09 m. Se sigue cumpliendo que Ωr<ωx0=0.3984 m/s.
mu_k=0.6; %coeficiente cinético
mu_s=0.7; %coeficiente estático
d=0.3; %2d distancia entre ruedas
m=1; %masa
om_r=0.3; %velocidad angular*radio
w=sqrt(mu_k*9.8/d); %frecuencia angular
hold on
colores=['r','k'];
x5=0.09; %posición inicial
for n=1:2
x0=x5; %posición inicial del c.m.
x1=sqrt(x0^2-(om_r/w)^2);
t1=asin(om_r/(x0*w))/w;
fplot(@(t) x0*cos(w*t), @(t) -w*x0*sin(w*t), [0,t1],
'color',colores(n))
s=(mu_s-mu_k)/(mu_s+mu_k);
t2=t1+(s+x1)/om_r;
fplot(@(t) x0*cos(w*t1)-om_r*(t-t1), @(t) -om_r+0*t, [t1,t2],
'color',colores(n))
t3=t2+2*atan(om_r/(w*s))/w;
fi=pi-atan(om_r/(w*s));
C=sqrt(s^2+(om_r/w)^2); %amplitud
fplot(@(t) C*cos(w*(t-t2)+fi), @(t) -w*C*sin(w*(t-t2)+fi), [t2,t3],
'color',colores(n))
x3=-s;
t4=t3+2*s/om_r;
fplot(@(t) x3+om_r*(t-t3), @(t) om_r+0*t, [t3,t4],
'color',colores(n))
t5=t4+atan(om_r/(w*s))/w; %periodo
fi=-atan(om_r/(w*s));
fplot(@(t) C*cos(w*(t-t4)+fi), @(t) -w*C*sin(w*(t-t4)+fi), [t4,t5],
'color',colores(n))
x5=C*cos(w*(t5-t4)+fi); %posición final
v5=-w*C*sin(w*(t5-t4)+fi);
end
hold off
xlabel('x (m)')
ylabel('v (m/s)')
grid on
title('Posición, velocidad')
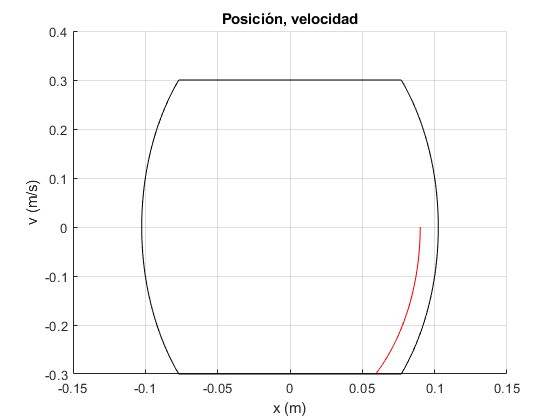
La trayectoria final (en el espacio de las fases) es independiente de la posición inicial
Referencias
Metzger E. An unusual case of Simple Harmonic Motion. Am. J. Phys. 40, August 1972, pp. 1167-1168
SU Guo-zhen. Solutions for a familiar mechanical problem. College Physics. Vol.40. n°6. June 2021

