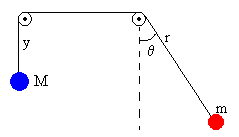
Las poleas tienen masa despreciable y la cuerda es inextensible, suficientemente larga para no preocuparnos de que el contrapeso M choque con la polea. Supondremos que la cuerda está siempre tensa y no tendremos en cuenta el rozamiento entre la cuerda y las poleas y en el movimiento de las masas puntuales m y M, por lo que la energía total del sistema de dos partículas permanece constante.

El vector posición, velocidad y aceleración en coordenadas polares

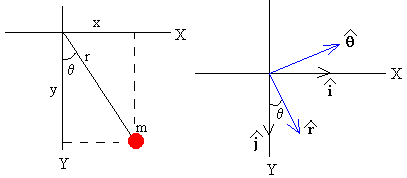
Establecemos un Sistema de Referencia Ortonormal, cuyos ejes son la dirección radial y la dirección perpendicular a la radial. Los vectores unitarios se señalan en la figura de la derecha.

Vector posición

El vector posición de la partícula oscilante es

${\displaystyle \overrightarrow{r}=r\widehat{r}}$

Vector velocidad

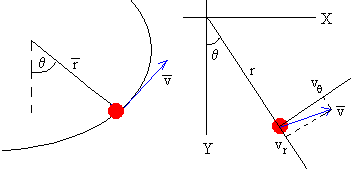
El vector velocidad es tangente a la trayectoria

Expresamos la velocidad de la partícula en coordenadas polares

${\displaystyle \overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\widehat{r}\frac{dr}{dt}+r\frac{d\widehat{r}}{dt}}$

Calculamos las componentes rectangulares de los vectores unitarios

${\displaystyle \begin{array}{l}\widehat{\theta }=\cos \theta ·\widehat{i}-\sin \theta ·\widehat{j}\hfill \\ \widehat{r}=\sin \theta ·\widehat{i}+\cos \theta ·\widehat{j}\hfill \end{array}}$

Calculamos las derivadas de los vectores unitarios

${\displaystyle \begin{array}{l}\frac{d\widehat{\theta }}{dt}=-(\sin \theta ·\widehat{i}+\cos \theta ·\widehat{j})\frac{d\theta }{dt}=-\widehat{r}\frac{d\theta }{dt}\hfill \\ \frac{d\widehat{r}}{dt}=(\cos \theta ·\widehat{i}-\sin \theta ·\widehat{j})\frac{d\theta }{dt}=\widehat{\theta }\frac{d\theta }{dt}\hfill \end{array}}$

Las componentes del vector velocidad en coordenadas polares son,

${\displaystyle \overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }}$

Vector aceleración

Derivamos la velocidad con respecto del tiempo

${\displaystyle \begin{array}{l}\frac{d\overrightarrow{v}}{dt}=\frac{d^{2}r}{d{t}^2}\widehat{r}+\frac{dr}{dt}\frac{d\widehat{r}}{dt}+\frac{dr}{dt}\frac{d\theta }{dt}\widehat{\theta }+r\frac{d^2\theta }{d{t}^2}\widehat{\theta }+r\frac{d\theta }{dt}\frac{d\widehat{\theta }}{dt}\hfill \\ \frac{d\overrightarrow{v}}{dt}=\frac{d^{2}r}{d{t}^2}\widehat{r}+\frac{dr}{dt}\frac{d\theta }{dt}\widehat{\theta }+\frac{dr}{dt}\frac{d\theta }{dt}\widehat{\theta }+r\frac{d^2\theta }{d{t}^2}\widehat{\theta }-r{\left(\frac{d\theta }{dt}\right)}^2\widehat{r}\hfill \\ \frac{d\overrightarrow{v}}{dt}=\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }\hfill \end{array}}$

Las componentes del vector aceleración en coordenadas polares valen

${\displaystyle a_r=\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2{a}_{\theta }=r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}}$

Ecuaciones del movimiento

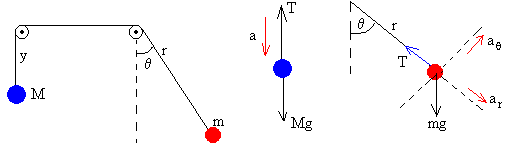
Las fuerzas que actúan sobre la partícula que oscila de masa m son:

• La tensión de la cuerda T
• El peso mg

Ecuación del movimiento en la dirección radial

mgcosθ-T=ma_r

Ecuación del movimiento en la perpendicular a la radial

-mgsinθ=ma_θ

Las fuerzas que actúan sobre el contrapeso de masa M son:

• La tensión de la cuerda T
• El peso Mg

Si y es la posición del contrapeso. La ecuación del movimiento es

${\displaystyle Mg-T=M\frac{d^{2}y}{d{t}^2}}$

Al alejarse la masa m aumenta r, el contrapeso M asciende, disminuye y, de modo que

${\displaystyle Mg-T=-M\frac{d^{2}r}{d{t}^2}}$

Eliminamos T entre la primera y tercera ecuación, llegamos a un sistema de dos ecuaciones diferenciales de segundo orden

${\displaystyle \begin{array}{l}mg\cos \theta -Mg-M\frac{d^{2}r}{d{t}^2}=m\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\\ -mg\text{sin}\theta =m\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\end{array}}$

Llamando μ=M/m

${\displaystyle \begin{array}{l}(1+\mu )\frac{d^{2}r}{d{t}^2}=r{\left(\frac{d\theta }{dt}\right)}^2+g(\cos \theta -\mu )\\ r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}+g\text{sin}\theta =0\end{array}}$

Principio de conservación de la energía

Situamos el nivel cero de energía potencial en la posición de las poleas

La energía potencial de los dos cuerpos es

E_p=-Mgy-mg·rcosθ

Teniendo en cuenta que y y r están relacionados, ya que la cuerda es inextensible y+r=l=cte.

E_p=Mgr-Mgl-mg·rcosθ

La energía cinética es

${\displaystyle E_k=\frac{1}{2}M{\left(\frac{dy}{dt}\right)}^2+\frac{1}{2}m\left({\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right)}$

La energía total se escribe

${\displaystyle E=\frac{1}{2}M{\left(\frac{dr}{dt}\right)}^2+\frac{1}{2}m\left({\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right)+gr(M-m\cos \theta )-Mgl}$

Eliminamos el término constante Mgl con una elección conveniente del nivel cero de energía potencial. Dividiendo entre m

${\displaystyle e=\frac{1}{2}\mu {\left(\frac{dr}{dt}\right)}^2+\frac{1}{2}\left({\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right)+gr(\mu -\cos \theta )}$

Ecuaciones de Lagrange

La lagrangiana L=E_k-E_p es

${\displaystyle L=\frac{1}{2}(M+m){\left(\frac{dr}{dt}\right)}^2+\frac{1}{2}m{r}^2{\left(\frac{d\theta }{dt}\right)}^2-gr(M-m\cos \theta )+Mgl}$

Comprobamos que obtenemos las mismas ecuaciones del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{r}}\right)-\frac{\partial L}{\partial r}=0\\ (M+m)\frac{d^{2}r}{d{t}^2}-mr{\left(\frac{d\theta }{dt}\right)}^2+g(M-m\cos \theta )=0\\ (\mu +1)\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2+g(\mu -\cos \theta )=0\\ \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{d}{dt}\left(r^2\frac{d\theta }{dt}\right)+gr\sin \theta =0\\ r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}+g\sin \theta =0\end{array}}$

Integración numérica de las ecuaciones del movimiento

Resolvemos mediante procedimientos numéricos el sistema de dos ecuaciones diferenciales de segundo orden con las siguientes condiciones iniciales, en el instante t=0, la posición inicial es r=r₀, θ=θ₀, y las componentes de la velocidad inicial son

${\displaystyle {\left(\frac{dr}{dt}\right)}_0{r}_0{\left(\frac{d\theta }{dt}\right)}_0}$

Calcularemos en cada instante la energía total e y la compararemos con la energía inicial e₀. Denominamos al cociente

${\displaystyle \left|\frac{e-e_0}{e_0}\right|·100}$

tanto por ciento de error. Cuando la energía e difiere de e₀ de modo que el cociente es mayor que la unidad, la trayectoria calculada puede que se desvíe significativamente de la real.

Observaremos una gran variedad de trayectorias: La partícula oscilante se moverá alrededor del origen si M>m, es decir, si μ>1. En caso contrario, la partícula se escapará.

Introduciremos valores de μ>1

La posición inicial habitual es r₀>0 entre 0 y 10 y θ₀=90º. La partícula oscilante está en el eje X. La distancia inicial al origen r₀>0, ya que para r₀=0 tenemos una singularidad en la segunda ecuación diferencial.

La velocidad inicial habitualmente es cero, (dr/dt)₀=0,  (dθ/dt)₀=0, pero se puede dar un valor a la componente radial (dr/dt)₀, cuando la partícula parte de una posición cercana al origen r₀≈0.

Se sugiere al lector la reproducción de las nueve trayectorias en cada una de las figuras 3, 4, 5 y 6 del artículo mencionado en las referencias

Probamos con μ=1.4, la partícula parte de r₀=1, θ₀=90°, en reposo (dr/dt)₀=0,  (dθ/dt)₀=0

mu=1.4; %cociente entre masas
x0=[1,0,pi/2,0]; %condiciones iniciales
%x(1) es r, x(2) es dr/dt, x(3) es theta, x(4) es dtheta/dt
fg=@(t,x)[x(2);x(1)*x(4)^2/(1+mu)+9.8*(cos(x(3))-mu)/(1+mu); 
x(4);-2*x(2)*x(4)/x(1)-9.8*sin(x(3))/x(1)];
[t,x]=ode45(fg,[0,10],x0);
plot(x(:,1).*cos(x(:,3)), x(:,1).*sin(x(:,3))) %trayectoria
grid on
xlabel('x')
ylabel('y');
title('oscilador de Atwood')

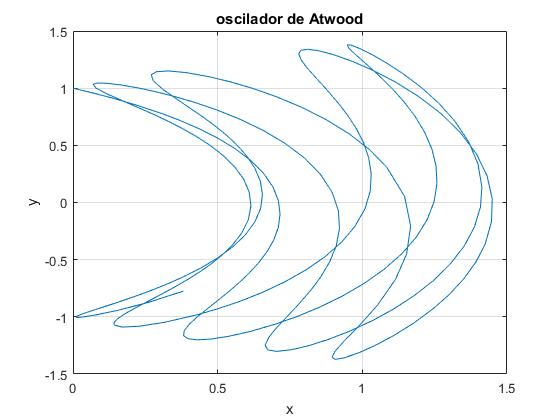
Comprobamos que la energía se mantiene constante y que el error es pequeño

>> e0=mu*x0(2)^2/2+(x0(2)^2+x0(1)^2*x0(4)^2)/2+9.8*x0(1)
*(mu-cos(x0(3)))
e0 =   13.7200
>> e=mu*x(:,2).^2/2+(x(:,2).^2+(x(:,1).^2).*x(:,4).^2)/2+9.8*x(:,1).
*(mu-cos(x(:,3)));
>> abs((e-e0)/e0)*100
ans =         0
         0
    0.0000
...
    0.1078
    0.1006
    0.0505
    0.0561

Probamos con μ=1.6, la partícula parte de las proximidades del origen r₀=0.01, θ₀=90°, con velocidad (dr/dt)₀=4,  (dθ/dt)₀=0

mu=1.6; %cociente entre masas
x0=[0.01,4,pi/2,0]; %condiciones iniciales
%x(1) es r, x(2) es dr/dt, x(3) es theta, x(4) es dtheta/dt
fg=@(t,x)[x(2);x(1)*x(4)^2/(1+mu)+9.8*(cos(x(3))-mu)/(1+mu); 
x(4);-2*x(2)*x(4)/x(1)-9.8*sin(x(3))/x(1)];
[t,x]=ode45(fg,[0,30],x0);
plot(x(:,1).*cos(x(:,3)), x(:,1).*sin(x(:,3))) %trayectoria
grid on
axis equal
xlabel('x')
ylabel('y');
title('oscilador de Atwood')

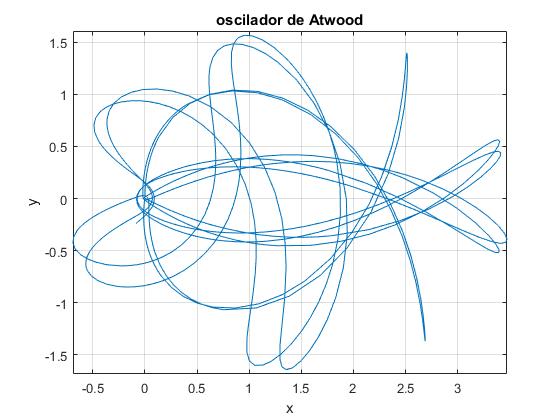
>> e0=mu*x0(2)^2/2+(x0(2)^2+x0(1)^2*x0(4)^2)/2+9.8*x0(1)*(mu-cos(x0(3)))
e0 =   20.9568 
>> e=mu*x(:,2).^2/2+(x(:,2).^2+(x(:,1).^2).*x(:,4).^2)/2+9.8*x(:,1).
*(mu-cos(x(:,3)));
>> abs((e-e0)/e0)*100
    ans =
         0
         0
    0.0000
    ....
        2.0654
    2.1245
    2.2503
    2.2496
    2.4229
....    

Vemos que el error se va incrementando a medida que transcurre el tiempo hasta cerca de un 2.5%

Actividades

Se introduce

• El cociente μ=M/m entre las masas del contrapeso y de la partícula, en el control titulado Cociente masas.

• La posición inicial de la partícula que oscila: r₀, distancia a la polea y θ₀, ángulo en grados que hace con la dirección vertical, en los controles titulados Distancia y Angulo, respectivamente

• La velocidad inicial de dicha partícula: la velocidad radial (dr/dt)₀, y la velocidad angular (dθ/dt)₀ en los controles titulados Velocidad radial y Velocidad angular, respectivamente.

Se pulsa el botón titulado Nuevo

Se dibuja la trayectoria de la partícula oscilante

Opcionalmente, se puede realizar ciertos ajustes:

• Se puede cambiar el paso de integración numérica de las ecuaciones diferenciales, seleccionando un valor en el control titulado Paso. Por ejemplo, si se selecciona 1/2, el paso por defecto se reduce a la mitad. Disminuyendo el paso, se puede reducir significativamente el error cometido en la integración del sistema de ecuaciones diferenciales.

• Se puede cambiar la escala. Para ver las trayectorias de la partícula oscilante cuando se aleja del origen, se aumenta la escala del dibujo, en el control titulado Escala.

En la parte superior izquierda se proporcionan los datos

• Tiempo, t
• Distancia al origen, r
• Angulo en radianes, θ
• Velocidad radial, dr/dt
• Velocidad angular, dθ/dt

El programa interactivo permite obtener una gran variedad de trayectorias, véase el artículo citado en las referencias, figuras 3, 4, 5 y 6

El programa interactivo se detiene cuando:

• La partícula oscilante llega al origen r<0
• El procedimiento numérico, no resuelve adecuadamente las ecuaciones del movimiento y la energía de la partícula se desvía apreciablemente de la energía inicial
• El número de puntos de la trayectoria supera 5000

Probar los siguientes casos:

• r₀=1 y θ₀=90º, velocidad inicial cero, μ=1.4, 1.5, 1.665, 2.2, 2.812, 4.8, 5.1, 7.7, 8.3, 9.8

• r₀=0.01,  θ₀=90º, (dr/dt)₀=4, (dθ/dt)₀=0, μ=1.182, 1.299, 3.0, 5.829

Referencias

Tufillaro N. B., Abott T. A. Griffiths D. J. Swinging Atwood’s machine. Am. J. Phys. 52 (10) October 1984, pp. 895-903