Estudiaremos el movimiento de una partícula de masa m=1 en el potencial dado por la función

${\displaystyle E_p(x)=1-\frac{x^2}{2}+\frac{x^4}{16}}$

La energía potencial presenta dos mínimos x=±2 y un máximo local, x=0. Véase la figura más abajo

Calculamos la derivada primera y la igualamos a cero. Calculamos la derivada segunda

${\displaystyle \begin{array}{l}\frac{d{E}_p(x)}{dx}=-x+\frac{x^3}{4}=0\{\begin{array}{l}x=0\\ x=\pm 2\end{array}\\ \frac{d^2{E}_p(x)}{d{x}^2}=-1+\frac{3}{4}{x}^2\end{array}}$

Para x=0, la deriva segunda es negativa, (máximo). Para x=±2, la derivada segunda es positiva (mínimo)

Dado el valor de la energía total E, determinamos el intervalo o intervalos en los que se puede mover la partícula.

${\displaystyle \frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+E_p(x)=E}$

Como la energía cinética es siempre positiva, la partícula se puede mover en aquellas posiciones en las que E≥E_p(x). Resolvemos la ecuación bicuadrada

${\displaystyle \begin{array}{l}\frac{x^4}{16}-\frac{x^2}{2}+1=E\\ x^2=4\left(1\pm \sqrt{E}\right)\end{array}}$

• Para E>1, se descarta el signo menos, la partícula se mueve en el intervalo

${\displaystyle \left[-2\sqrt{1+\sqrt{E}},2\sqrt{1+\sqrt{E}}\right]}$

• Si E<1, la partícula se puede mover en uno o en el otro intervalo

${\displaystyle \left[-2\sqrt{1+\sqrt{E}},-2\sqrt{1-\sqrt{E}}\right],\left[2\sqrt{1-\sqrt{E}},2\sqrt{1+\sqrt{E}}\right]}$

Representamos la energía potencial y los intervalos para dos valores de la energía total E=1.25, 0.5

f=@(x) 1-x.^2/2+x.^4/16; %energía potencial
fplot(f,[-3.1,3.1])
E=1.25;
x1=-2*sqrt(1+sqrt(E));
x2=-x1;
line([x1,x2],[f(x1),f(x2)],'color','b')
line([x1,x1],[0,f(x1)],'lineStyle','--','color','k')
line([x2,x2],[0,f(x2)],'lineStyle','--','color','k')

E=0.5;
x1=-2*sqrt(1+sqrt(E));
x2=-2*sqrt(1-sqrt(E));
line([x1,x2],[f(x1),f(x2)],'color','r')
line([x1,x1],[0,f(x1)],'lineStyle','--','color','k')
line([x2,x2],[0,f(x2)],'lineStyle','--')
x1=2*sqrt(1-sqrt(E));
x2=2*sqrt(1+sqrt(E));
line([x1,x2],[f(x1),f(x2)],'color','r')
line([x1,x1],[0,f(x1)],'lineStyle','--','color','k')
line([x2,x2],[0,f(x2)],'lineStyle','--','color','k')

grid on
xlabel('x')
ylabel('E_p(x)')
title('Energía potencial')

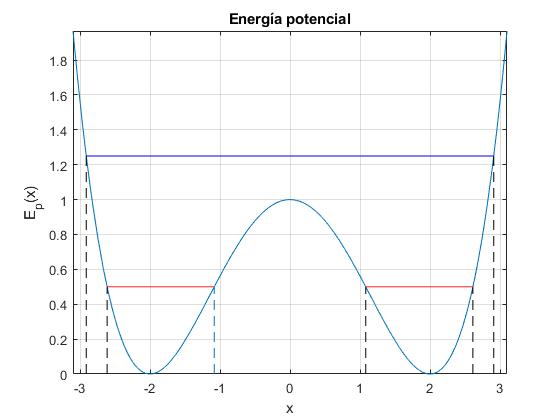
Como la energía total E es positiva, para simplificar la notación escribimos E=e²

En la ecuación de la energía despejamos dt e integramos

${\displaystyle t=\pm {\displaystyle \underset{x_0}{\overset{x}{\int }}\frac{dx}{\sqrt{\frac{2}{m}\left(e^2-E_p(x)\right)}}}}$

Supongamos que el móvil de masa m=1 parte de la posición del extremo derecho del intervalo, $x_0=2\sqrt{1+e}$, con velocidad inicial negativa (dx/dt)₀<0

${\displaystyle t=-{\displaystyle \underset{2\sqrt{1+e}}{\overset{x}{\int }}\frac{dz}{\sqrt{2(e^2-1)+z^2-\frac{z^4}{8}}}}=-\sqrt{8}{\displaystyle \underset{2\sqrt{1+e}}{\overset{x}{\int }}\frac{dz}{\sqrt{\left(4(e+1)-z^2\right)\left(z^2+4(e-1)\right)}}}}$

Hacemos el cambio de variable,

${\displaystyle \begin{array}{l}z=2\sqrt{1+e}·\cos \phi \\ dz=-2\sqrt{1+e}·\sin \phi ·d\phi \end{array}}$

El resultado es

${\displaystyle t=\sqrt{2}{\displaystyle \underset{0}{\overset{\Phi (x)}{\int }}\frac{d\phi }{\sqrt{\left((1+e){\cos }^2\phi +(e-1)\right)}}}=\sqrt{2}{\displaystyle \underset{0}{\overset{\Phi (x)}{\int }}\frac{d\phi }{\sqrt{\left(2e-(1+e){\sin }^2\phi \right)}}}=\frac{1}{\sqrt{e}}{\displaystyle \underset{0}{\overset{\Phi (x)}{\int }}\frac{d\phi }{\sqrt{\left(1-\frac{1+e}{2e}{\sin }^2\phi \right)}}}}$

• Para e>1, k²=(1+e)/(2e)≤1

${\displaystyle \sqrt{e}·t={\displaystyle \underset{0}{\overset{\Phi (x)}{\int }}\frac{d\phi }{\sqrt{\left(1-k^2{\sin }^2\phi \right)}}}\{\begin{array}{l}{k}^2=\frac{1+e}{2e}\\ \Phi (x)=\arccos \left(\frac{x}{2\sqrt{1+e}}\right)\end{array}}$

Despejamos x en función del tiempo t, empleando la función elíptica sn de Jacobi

${\displaystyle \begin{array}{l}\text{sn}\left(\sqrt{e}·t|k\right)=\sin \left(\Phi (x)\right)\\ \text{sn}\left(\sqrt{e}·t|k\right)=\sqrt{1-{\cos }^2\left(\Phi (x)\right)}\\ \text{sn}\left(\sqrt{e}·t|k\right)=\sqrt{1-{\left(\frac{x}{2\sqrt{1+e}}\right)}^2}\\ x^2=4(1+e)·{\text{cn}}^2\left(\sqrt{e}·t|k\right)\\ x=2\sqrt{1+e}·\text{cn}\left(\sqrt{e}·t|k\right)\end{array}}$

Se ha utilizado la relación, sn²(x|k)+cn²(x|k)=1

Derivando respecto del tiempo, obtenemos la velocidad del móvil

${\displaystyle \frac{dx}{dt}=-2\sqrt{e(1+e)}·\text{sn}\left(\sqrt{e}·t|k\right)\text{dn}\left(\sqrt{e}·t|k\right)}$

• Para e=1, k²=(1+e)/(2e)=1

Para este valor límite de k², la posición y velocidad toman las expresiones

${\displaystyle \begin{array}{l}x=2\sqrt{2}·\frac{1}{\cosh t}\\ \frac{dx}{dt}=-2\sqrt{2}·\tanh t·\frac{1}{\cosh t}=-2\sqrt{2}\frac{\sinh t}{{\cosh }^{2}t}\end{array}}$

• Para e<1, k²=(1+e)/(2e)>1

Para estos valores de k² fuera del intervalo [0,1], la posición y velocidad toman las expresiones

${\displaystyle \begin{array}{l}x=2\sqrt{1+e}·\text{dn}\left(\sqrt{\frac{1+e}{2e}}\sqrt{e}·t|\frac{1}{k}\right)=2\sqrt{1+e}\text{·dn}\left(\sqrt{\frac{1+e}{2}}·t|\frac{1}{k}\right)\\ \frac{dx}{dt}=-2\sqrt{e(1+e)}·\frac{1}{\sqrt{\frac{1+e}{2e}}}\text{sn}\left(\sqrt{\frac{1+e}{2}}·t|\frac{1}{k}\right)\text{cn}\left(\sqrt{\frac{1+e}{2}}·t|\frac{1}{k}\right)\\ =-2\sqrt{2e}\text{·sn}\left(\sqrt{\frac{1+e}{2}}·t|\frac{1}{k}\right)\text{cn}\left(\sqrt{\frac{1+e}{2}}·t|\frac{1}{k}\right)\end{array}}$

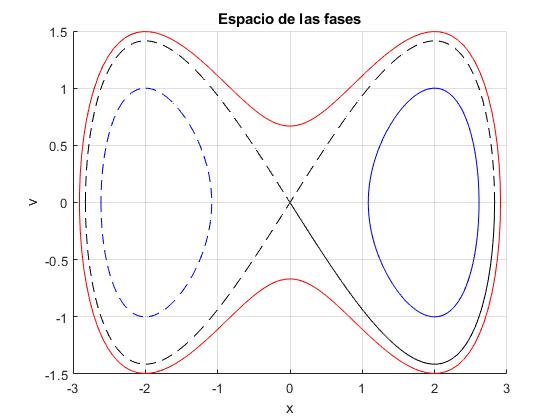
Representamos la trayectoria de un móvil en el espacio de las fases (x, v) para las energías:

• E=1.25. La partícula se mueve en el intervalo $\left[-2\sqrt{1+\sqrt{E}},2\sqrt{1+\sqrt{E}}\right]$, la trayectoria en el espacio de las fases es cerrada y el tiempo que tarda en completarla es

${\displaystyle P=\frac{4K(k)}{\sqrt{e}}}$

• E=1. Como el caso anterior, el móvil parte de la posición inicial $x_0=2\sqrt{1+e}$, tardando un tiempo infinito en alcanzar el origen x=0

• E=0.5. La partícula se mueve en el intervalo $\left[2\sqrt{1-\sqrt{E}},2\sqrt{1+\sqrt{E}}\right]$ alrededor del mínimo x=2, la trayectoria en el espacio de las fases es cerrada, tardando un tiempo P en completarla. También es posible que la partícula se mueva en el intervalo centrado en x=-2. Pero no es posible que una partícula con energía E<1, pase de un intervalo al otro

${\displaystyle P=\frac{2K(k)}{\sqrt{(1+e)/2}}}$

e=sqrt(1.25);
m2=(1+e)/(2*e);
K=ellipke(m2);
P=4*K/sqrt(e); %periodo
t=linspace(0,P,200);
[sn,cn,dn]=ellipj(sqrt(e)*t,m2);
x=2*sqrt(1+e)*cn;
v=-2*sqrt(1+e)*sn.*dn;
hold on
plot(x,v, 'r')

%e=1;
t=linspace(0,10,200);
x=2*sqrt(2)./cosh(t);
v=-2*sqrt(2)*sinh(t)./cosh(t).^2;
plot(x,v,'k')
plot(-x,v,'k','lineStyle','--')
plot(x,-v,'k','lineStyle','--')
plot(-x,-v,'k','lineStyle','--')

e=sqrt(0.5);
m2=(1+e)/(2*e);
K=ellipke(1/m2);
P=2*K/sqrt((1+e)/2); %periodo
t=linspace(0,P,200);
[sn,cn,dn]=ellipj(sqrt((1+e)/2)*t,1/m2);
x=2*sqrt(1+e)*dn;
v=-2*sqrt(2)*e*sn.*cn;
plot(x,v,'b')
plot(-x,v,'b','lineStyle','--')

hold off
xlabel('x')
ylabel('v')
title('Espacio de las fases')
grid on

Referencias

Alain J. Brizard. A primer on elliptic functions with applications in classical mechanics. November 26, 2007. https://arxiv.org/abs/0711.4064.