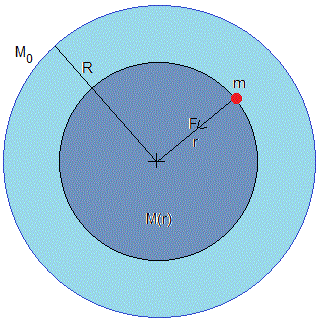
Sea una estrella de masa M₀ y radio R. Una hipotética partícula de masa m se mueve por su interior. La fuerza sobre la partícula cuando se encuentra a una distancia r de su centro es

${\displaystyle \overrightarrow{F}=-G\frac{M(r)m}{r^2}\widehat{r}}$

Donde M(r) es la masa de la estrella contenida en la esfera de radio r. Naturalmente, M(R)=M₀ es la masa de la estrella.

En la página titulada Ecuación de la trayectoria, en el apartado 'Ecuación del movimiento'. dedujimos

${\displaystyle \frac{d^{2}u}{d{\theta }^2}+u=\frac{GM(r)m^2}{L^2}}$

donde u=1/r y L es el momento angular, una de las constantes del movimiento

${\displaystyle L=m{r}^2\frac{d\theta }{dt}\text{=cte}}$

Esta ecuación, se escribe de otra forma más conveniente para este problema

${\displaystyle \begin{array}{l}\frac{d^2\left(Ru\right)}{d{\theta }^2}+Ru=\frac{GRM(r)m^2}{L^2}\\ \frac{d^2\eta }{d{\theta }^2}+\eta =\frac{GRM(r)}{{\ell }^2},\ell =r^2\frac{d\theta }{dt}\end{array}}$

donde η=R/r

Distribución de masa

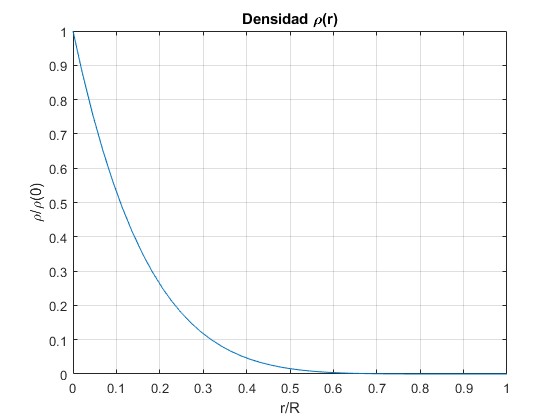
La densidad de la estrella no es constante

${\displaystyle \rho (r)=\rho (0){\left(1-\frac{r}{R}\right)}^6}$

f=@(x) (1-x).^6;
fplot(f,[0,1])
grid on
xlabel('r/R')
ylabel('\rho/\rho(0)')
title('Densidad \rho(r)')

Conocida la densidad ρ(r) calculamos la masa M(r) contenida en la esfera de radio r

${\displaystyle M(r)=\{\begin{array}{l}{\displaystyle \underset{0}{\overset{r}{\int }}\rho (r)\left(4\pi r^2\right)dr,r<R}\\ M_{0}r\ge R\end{array}}$

Integramos

${\displaystyle \begin{array}{l}{\left(1-\frac{r}{R}\right)}^6=\left(\begin{array}{c}6\\ 0\end{array}\right){\left(\frac{r}{R}\right)}^6-\left(\begin{array}{c}6\\ 1\end{array}\right){\left(\frac{r}{R}\right)}^5+\left(\begin{array}{c}6\\ 2\end{array}\right){\left(\frac{r}{R}\right)}^4-\left(\begin{array}{c}6\\ 3\end{array}\right){\left(\frac{r}{R}\right)}^3+\left(\begin{array}{c}6\\ 4\end{array}\right){\left(\frac{r}{R}\right)}^2-\left(\begin{array}{c}6\\ 5\end{array}\right)\left(\frac{r}{R}\right)+\left(\begin{array}{c}6\\ 6\end{array}\right)\\ \left(\begin{array}{c}m\\ n\end{array}\right)=\frac{m(m-1)(m-2)\mathrm{...}(m-n+1)}{1·2·\mathrm{3...}·n}=\frac{m!}{n!·\left(m-n\right)!}\\ {\left(1-\frac{r}{R}\right)}^6={\left(\frac{r}{R}\right)}^6-6{\left(\frac{r}{R}\right)}^5+15{\left(\frac{r}{R}\right)}^4-20{\left(\frac{r}{R}\right)}^3+15{\left(\frac{r}{R}\right)}^2-6\frac{r}{R}+1\end{array}}$

>> syms x;
>> expand((1-x)^6)
 ans =x^6 - 6*x^5 + 15*x^4 - 20*x^3 + 15*x^2 - 6*x + 1

${\displaystyle \begin{array}{l}M(r)=4\pi {\displaystyle \underset{0}{\overset{r}{\int }}\rho (r)r^{2}dr=}\\ 4\pi \rho (0){\displaystyle \underset{0}{\overset{r}{\int }}\left\{{\left(\frac{r}{R}\right)}^6-6{\left(\frac{r}{R}\right)}^5+15{\left(\frac{r}{R}\right)}^4-20{\left(\frac{r}{R}\right)}^3+15{\left(\frac{r}{R}\right)}^2-6\frac{r}{R}+1\right\}{r}^{2}dr=}\\ 4\pi \rho (0){\displaystyle \underset{0}{\overset{r}{\int }}\left\{\frac{r^8}{R^6}-6\frac{r^7}{R^5}+15\frac{r^6}{R^4}-20\frac{r^5}{R^3}+15\frac{r^4}{R^2}-6\frac{r^3}{R}+r^2\right\}dr=}\\ 4\pi \rho (0)\left\{\frac{1}{9}\frac{r^9}{R^6}-\frac{6}{8}\frac{r^8}{R^5}+\frac{15}{7}\frac{r^7}{R^4}-\frac{20}{6}\frac{r^6}{R^3}+\frac{15}{5}\frac{r^5}{R^2}-\frac{6}{4}\frac{r^4}{R}+\frac{1}{3}{r}^3\right\}\\ M(r)=4\pi \rho (0)\left\{\frac{1}{9}\frac{r^9}{R^6}-\frac{3}{4}\frac{r^8}{R^5}+\frac{15}{7}\frac{r^7}{R^4}-\frac{10}{3}\frac{r^6}{R^3}+3\frac{r^5}{R^2}-\frac{3}{2}\frac{r^4}{R}+\frac{1}{3}{r}^3\right\}\\ M_0=M(R)=4\pi \rho (0)\frac{R^3}{252}\\ \frac{M(r)}{M_0}=252\left\{\frac{1}{9}{\left(\frac{r}{R}\right)}^9-\frac{3}{4}{\left(\frac{r}{R}\right)}^8+\frac{15}{7}{\left(\frac{r}{R}\right)}^7-\frac{10}{3}{\left(\frac{r}{R}\right)}^6+3{\left(\frac{r}{R}\right)}^5-\frac{3}{2}{\left(\frac{r}{R}\right)}^4+\frac{1}{3}{\left(\frac{r}{R}\right)}^3\right\}\end{array}}$

>> format rat
>> 1/9-3/4+15/7-10/3+3-3/2+1/3
ans =       1/252 

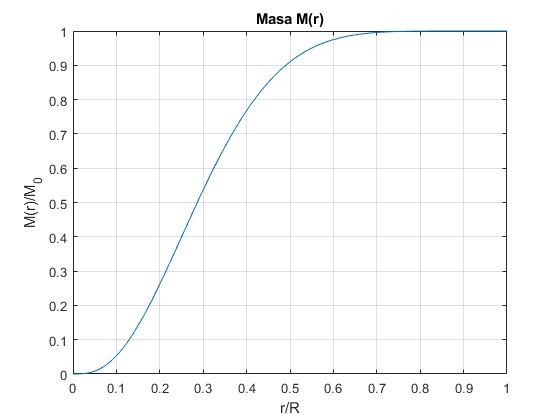
REpresentamos la masa M(r)/M₀ en función de r/R

f=@(x) 252*(x.^9/9-3*x.^8/4+15*x.^7/7-10*x.^6/3+3*x.^5-3*x.^4/2+x.^3/3);
fplot(f,[0,1])
grid on
xlabel('r/R')
ylabel('M(r)/M_0')
title('Masa M(r)')

Ecuación del movimiento

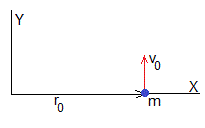
La partícula parte de la posición r₀, θ=0 que es una posición de retorno (la distancia radial es máxima o mínima) dr/dt=0. El momento angular constante vale

${\displaystyle \ell =r_0{v}_0}$

La ecuación del movimiento es

${\displaystyle \{\begin{array}{l}\frac{d^2\eta }{d{\theta }^2}+\eta =252\frac{GR{M}_0}{{\left(r_0{v}_0\right)}^2}\left\{\frac{1}{9}\frac{1}{{\eta }^9}-\frac{3}{4}\frac{1}{{\eta }^8}+\frac{15}{7}\frac{1}{{\eta }^7}-\frac{10}{3}\frac{1}{{\eta }^6}+3\frac{1}{{\eta }^5}-\frac{3}{2}\frac{1}{{\eta }^4}+\frac{1}{3}\frac{1}{{\eta }^3}\right\},r<R\\ \frac{d^2\eta }{d{\theta }^2}+\eta =\frac{GR{M}_0}{{\left(r_0{v}_0\right)}^2},r\ge R\end{array}}$

Las condiciones iniciales

${\displaystyle \begin{array}{l}\theta =\mathrm{0,}{\eta }_0=\frac{R}{r_0}\\ \frac{d\eta }{d\theta }=\frac{d\frac{R}{r}}{d\theta }=-\frac{R}{r^2}\frac{dr}{d\theta }=-\frac{R}{r^2}\frac{dr}{dt}\frac{dt}{d\theta }\\ {\left(\frac{d\eta }{d\theta }\right)}_0=-\frac{R}{r_0^2}{\left(\frac{dr}{dt}\right)}_0\frac{r_0}{v_0}=-\frac{R}{r_0}{\left(\frac{dr}{dt}\right)}_0\frac{1}{v_0}=0\end{array}}$

Trayectorias

Los datos del Sol son

• Masa M₀=1.9905·10³⁰kg
• Radio, R=6.9598·10⁸ m

En la mayor parte de las páginas de este curso, se ha utilizado el procedimiento ode45 de MATLAB para resolver una ecuación diferencial o un sistema de ecuaciones diferenciales. Veremos que éste procedimiento no es el más adecuado para resolver un sistema conservativo como es este caso

• Resolvemos la ecuación diferencial por el procedimento ode45 de MATLAB con las siguientes datos

• Distancia inicial r₀/R=4/5.
• Velocidad inicial, v₀=129 km/s
• Angulo inicial, θ=0, final θ=10·π (5 vueltas)

R=6.9598e8; %radio Sol
r0=4*R/5;
v0=129e3;
k=252*6.67e-11*R*1.9905e30/(r0*v0)^2;
f=@(t,x) [x(2); -x(1)+k*(1/(9*x(1)^9)-3/(4*x(1)^8)+15/(7*x(1)^7)-
10/(3*x(1)^6)+3/(x(1)^5)-3/(2*x(1)^4)+1/(3*x(1)^3))];
[t,x]=ode45(f,[0,10*pi],[R/r0,0]);
hold on
ang=linspace(0, 2*pi, 200);
fill(cos(ang),sin(ang),'c')
plot(cos(ang),sin(ang),'b')
plot(cos(t)./x(:,1), sin(t)./x(:,1),'r')
hold off
grid on
axis equal
xlabel('x/R')
ylabel('y/R')
title('Trayectorias')



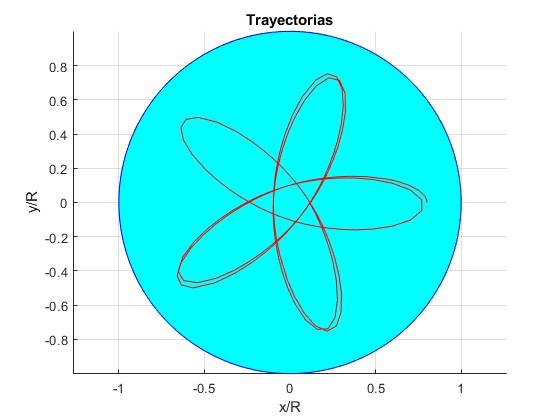
• Por el procedimiento de Runge-Kutta

function solar_4  
    R=6.9598e8; %radio Sol
    r0=4*R/5;
    v0=129e3;
    k=6.67e-11*R*1.9905e30/(r0*v0)^2;
    [t,x,~]=rk_2(@f1,0,10*pi,R/r0,0);
    hold on
    ang=linspace(0, 2*pi, 200);
    hold on
    fill(cos(ang),sin(ang),'c')
    plot(cos(ang),sin(ang),'b')
    plot(cos(t)./x, sin(t)./x,'r')
    hold off
    grid on
    axis equal
    xlabel('x/R')
    ylabel('y/R')
    title('Trayectorias')
    
    function res=f1(~,x,~)
        if (1/x<1) 
            res=-x+252*k*(1/(9*x^9)-3/(4*x^8)+15/(7*x^7)-
10/(3*x^6)+3/x^5-3/(2*x^4)+1/(3*x^3));
        else
           res=-x+k;
        end
    end
    
    function [t,x,v] =rk_2(f,t0,tf,x0,v0)
          h=0.01;
          n=floor((tf-t0)/h);
          t=(t0:h:tf)'; %vector columna
    %reserva memoria para n+1 elementos del vector x y v
          x=zeros(n+1,1); 
          v=zeros(n+1,1);
          x(1)=x0; v(1)=v0;
          
          for i=1:n
            k1=h*v(i);
            l1=h*f(t(i),x(i),v(i));
            k2=h*(v(i)+l1/2);
            l2=h*f(t(i)+h/2,x(i)+k1/2,v(i)+l1/2);
            k3=h*(v(i)+l2/2);
            l3=h*f(t(i)+h/2,x(i)+k2/2,v(i)+l2/2);
            k4=h*(v(i)+l3);
            l4=h*f(t(i)+h,x(i)+k3,v(i)+l3);
            
            x(i+1)=x(i)+(k1+2*k2+2*k3+k4)/6;
            v(i+1)=v(i)+(l1+2*l2+2*l3+l4)/6;        
          end
     end 
end

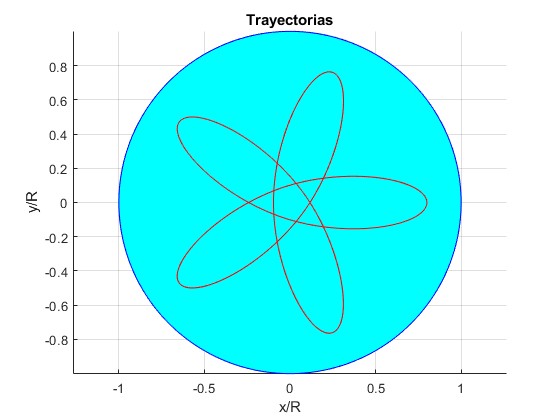
Elegimos, por tanto, el procedimiento de Runge-Kutta

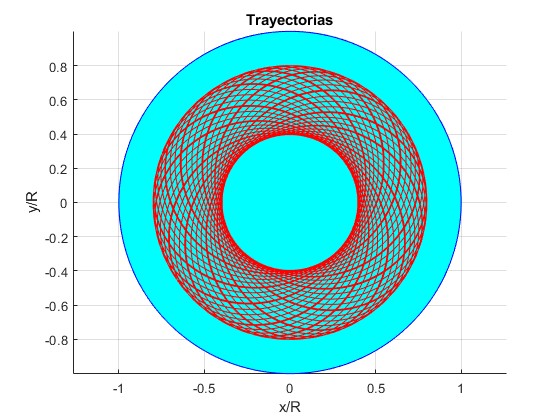
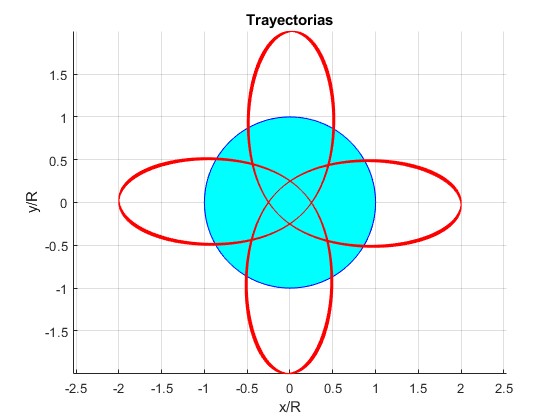
Ejemplos con distancia inicial r₀/R=4/5, ángulo final θ=200·π (100 vueltas)

• Velocidad inicial, v₀=488.18 km/s



• Velocidad inicial, v₀= 39.534 km/s



• Velocidad inicial, v₀= 161.30 km/s



• Velocidad inicial, v₀= 370.79 km/s

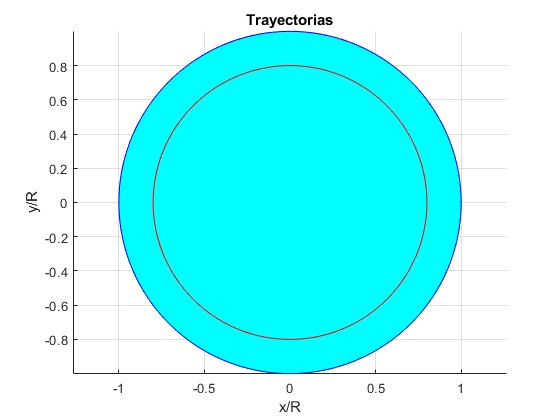
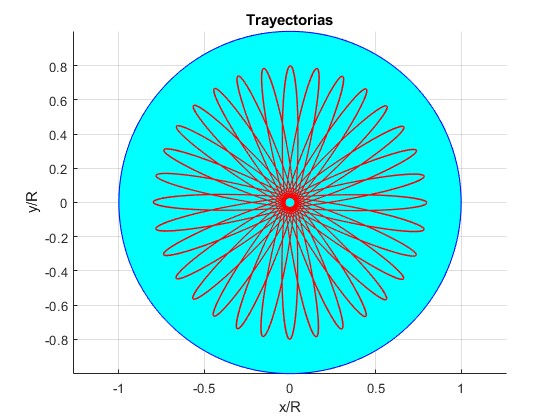
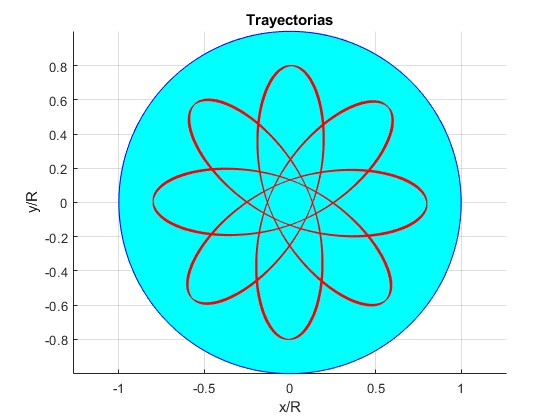
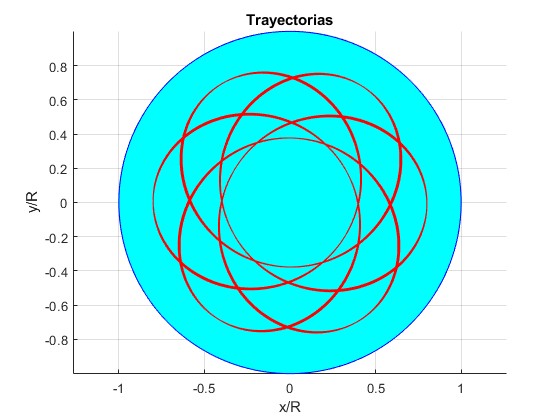
Ejemplos con distancia inicial r₀/R=4/5, ángulo final θ=100·π (50 vueltas)

• Velocidad inicial, v₀= 80.925 km/s



• Velocidad inicial, v₀=222.99 km/s



• Velocidad inicial, v₀=380.79 km/s

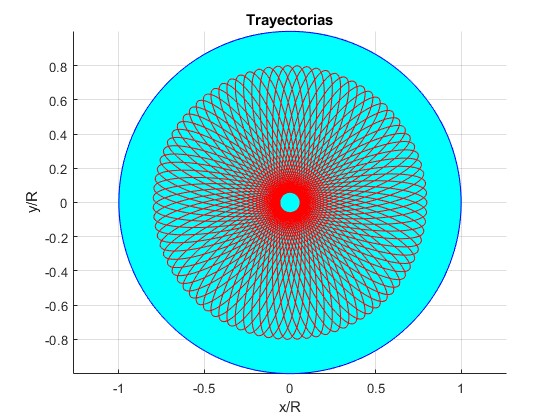
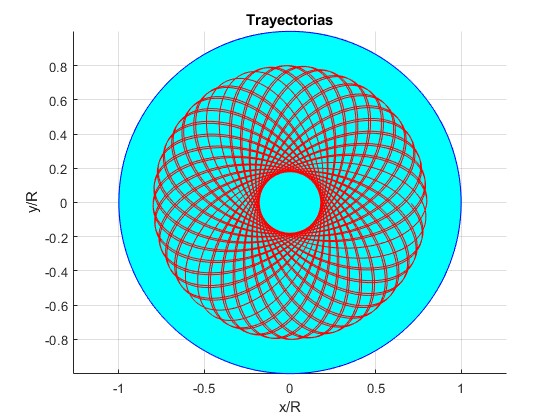
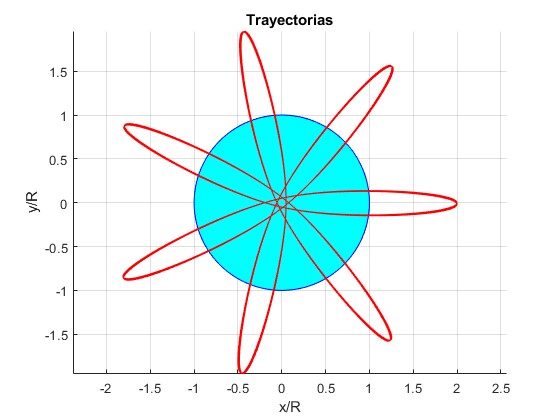
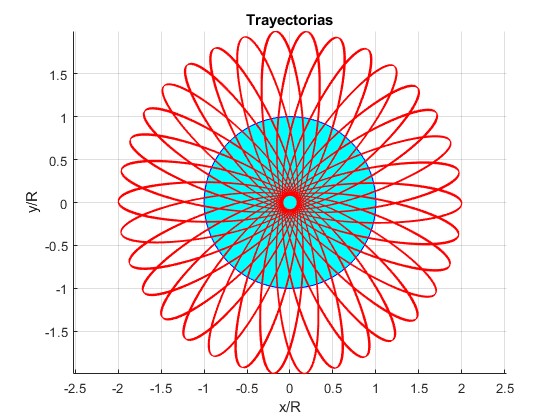
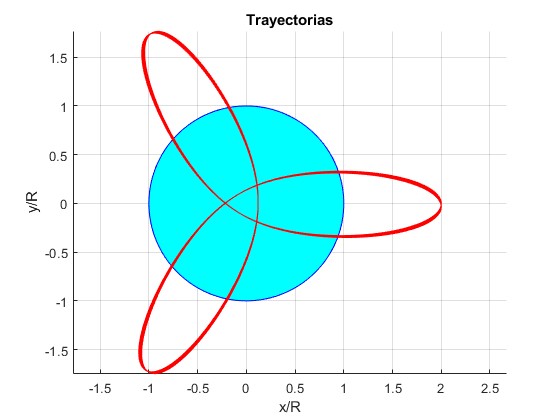
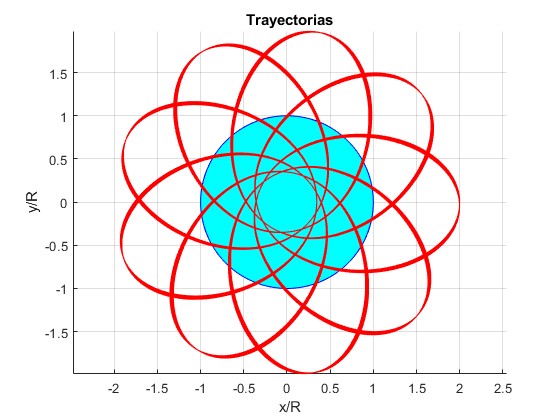
Ejemplos con distancia inicial r₀/R=2, ángulo final θ=200·π (100 vueltas)

• Velocidad inicial, v₀=30.196 km/s



• Velocidad inicial, v₀=50.065 km/s



• Velocidad inicial, v₀=71.115 km/s



• Velocidad inicial, v₀=105.95 km/s



• Velocidad inicial, v₀=159.74 km/s

Actividades

Se introduce

• La distancia radial r₀/R en el control titulado r₀/R. Un número menor que 2
• La velocidad v₀ en km/s en el control titulado v₀
• El ángulo total, θ, en el control titulado Vueltas

Se pulsa el botón titulado Nuevo

Referencias

Vitorio A. De Lorenci, David I. Kaiser, Patrick Peter. Orbital motion of primordial black holes crossing Sun-like stars. Am. J. Phys. 93 (12), December 2025. pp. 943-950