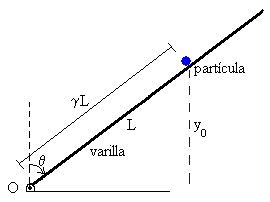
Movimiento de la partícula

Ya hemos estudiado el movimiento de caída de los cuerpos en el capítulo de Cinemática. La partícula se deja caer desde una altura y₀=γLcos θ₀  partiendo del reposo

${\displaystyle y=y_0-\frac{1}{2}g{t}^2}$

El tiempo P_p que tarda en llegar al suelo y=0 es

${\displaystyle P_p=\sqrt{\frac{2y_0}{g}}=\sqrt{\frac{2\gamma L\cos {\theta }_0}{g}}}$

Movimiento de rotación la varilla

La varilla es un sólido rígido en rotación alrededor de un eje fijo perpendicular a la varilla y que pasa por su extremo O.

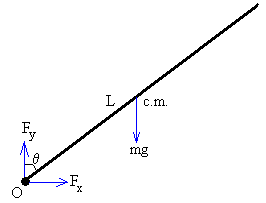
Las fuerzas que actúan sobre la varilla son:

• El peso mg que actúa en el centro de masa.

• La fuerza que ejerce el eje sobre la varilla en su extremo O. Una fuerza cuyo módulo y dirección son desconocidas, o bien, dos fuerzas mutuamente perpendiculares F_x y F_y.

La ecuación de la dinámica de la rotación alrededor de un eje fijo, es

${\displaystyle I_0\alpha =M{I}_0\frac{d^2\theta }{d{t}^2}=M}$

• I_O es el momento de inercia de la varilla respecto de un eje perpendicular a la misma que pasa por su extremo O.

${\displaystyle I_o=\frac{1}{12}m{L}^2+m{\left(\frac{L}{2}\right)}^2=\frac{1}{3}m{L}^2}$

• M es el momento de las fuerzas que actúan sobre la varilla respecto de O, tiene el mismo sentido que la aceleración angular α.

M=mg(L/2)·sin θ

• La aceleración angular α no es constante, depende del ángulo θ que hace la varilla con el suelo.

${\displaystyle \alpha =\frac{3g}{2L}\text{sin}\theta }$

Para obtener el ángulo θ que hace la varilla con el suelo en función del tiempo t, se integra la ecuación diferencial mediante procedimientos numéricos.

${\displaystyle \frac{d^2\theta }{d{t}^2}-\frac{3g}{2L}\sin \theta =0}$

con las condiciones iniciales siguientes: en el instante t=0, la varilla está inclinada un ángulo θ=θ₀ (10°) y parte del reposo, ω=dθ/dt=0

L=2; %longitud de la varilla
k=3*9.8/(2*L);
f=@(t,x) [x(2);k*sin(x(1))]; 
ang=10*pi/180; %ángulo inicial
opts=odeset('events',@varilla_ode45);
[t,x,te]=ode45(f,[0,4],[ang,0], opts);
plot(t,x(:,1))
set(gca,'YTick',0:pi/12:pi/2)
set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','pi/3','5\pi/12','\pi/2'})
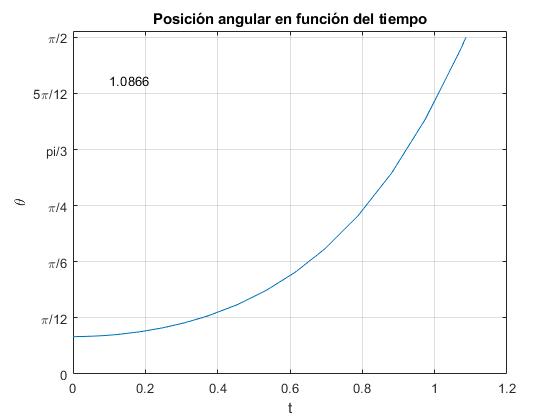
text(0.1,pi/2-0.2,num2str(te)) %tiempo de caída
grid on
xlabel('t')
ylabel('\theta');
title('Posición angular en función del tiempo')

Definimos una función para que el proceso de integración se detenga cuando la posición de la varilla sea π/2, el instante t en el que ocurre se guarda en la variable te

function [detect,stopin,direction]=varilla_ode45(~,x)
    detect=x(1)-pi/2; 
    stopin=1;
    direction=1; 
end

Estudio energético

La energía potencial de la varilla es la energía potencial de una partícula de masa m situada en el c.m. de la varilla E=mg(L/2)·cosθ₀. La energía potencial se convierte en energía cinética de rotación. El principio de conservación de la energía se escribe.

${\displaystyle E=\frac{1}{2}\left(\frac{1}{3}m{L}^2\right){\omega }^2+mg\frac{L}{2}\text{cos}\theta }$

Comprobamos que la energía se mantiene aproximadamente constante e igual a la inicial, mgLcos(θ₀)/2

>> L*9.8*cos(ang)/2
ans =    9.6511
>> E=L^2*x(:,2).^2/6+9.8*L*cos(x(:,1))/2
    9.6511
    9.6511
    ....
    9.6603
    9.6611
    9.6622

La ecuación del movimiento nos permite calcular la posición angular θ y la velocidad angular ω de la varilla en función del tiempo t. Sin embargo, el principio de conservación de la energía nos permite calcular la velocidad angular ω en función de la posición θ.

${\displaystyle \omega =\frac{d\theta }{dt}=\sqrt{\frac{3g}{L}(\cos {\theta }_0-\cos \theta )}}$

Supongamos que la varilla parte de la posición θ₀≈0, (la posición θ₀=0 es de equilibrio inestable)

${\displaystyle \frac{d\theta }{dt}=\sqrt{\frac{6g}{L}}\sin \left(\frac{\theta }{2}\right)}$

Integramos, véase la la tabla de integrales

${\displaystyle \begin{array}{l}{\displaystyle \underset{{\theta }_0\approx 0}{\overset{\theta }{\int }}\frac{d\theta }{\sin \left(\frac{\theta }{2}\right)}}=\sqrt{\frac{6g}{L}}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ 2\log \left(\tan \left(\frac{\theta }{4}\right)\right)-2\alpha =\sqrt{\frac{6g}{L}}t\\ \tan \left(\frac{\theta }{4}\right)=\exp \left(\sqrt{\frac{3g}{2L}}t+\alpha \right)\\ \theta =4\arctan \left\{\exp \left(\sqrt{\frac{3g}{2L}}t+\alpha \right)\right\}\end{array}}$

La varilla llega al suelo θ=π/2, en el instante t_f

${\displaystyle t_f=\frac{\tan \left(\frac{\pi }{8}\right)-\alpha }{\sqrt{\frac{3g}{2L}}}}$

Comparamos la solución numérica y la analítica aproximada cuando la varilla se deja caer desde la posición angular casi vertical, θ₀=1° (π/180)

function varilla
    L=2; %longitud de la varilla
    ang=1*pi/180;  %posición de partida
    k=3*9.8/(2*L);
    f=@(t,x) [x(2);k*sin(x(1))]; 
    opts=odeset('events',@varilla_ode45);
    [t,x, te]=ode45(f,[0,4],[ang,0], opts);
    hold on
    plot(t,x(:,1))
    set(gca,'YTick',0:pi/12:pi/2)
    set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','pi/3','5\pi/12','\pi/2'})
  
    alfa=log(tan(ang/4));
    tf=(log(pi/8)-alfa)/sqrt(9.8*3/(2*L));
    th=@(t) 4*exp(sqrt(9.8*3/(2*L))*t+alfa);
    fplot(th,[0,tf])
    hold off
    disp([te,tf])
    grid on
    legend('numérica', 'analítica','location','best')
    xlabel('t')
    ylabel('\theta');
    title('Posición angular en función del tiempo')

    function [detect,stopin,direction]=varilla_ode45(~,x)
        detect=x(1)-pi/2; 
        stopin=1;
        direction=1; 
    end
end

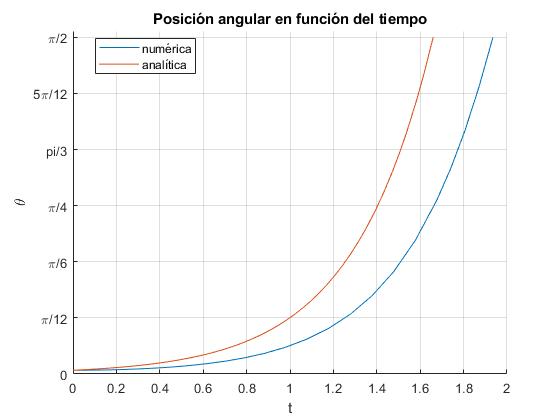
Los tiempos calculados son, respectivamente

    1.9352    1.6598

El primero, 1.9352 s, es el que más se aproxima al tiempo exacto, que vamos a calcular en el próximo apartado

Tiempo que tarda la varilla en caer al suelo

Integrando entre θ₀ y π/2, obtenemos el tiempo P_v que tarda la varilla en llegar al suelo.

${\displaystyle P_v=\sqrt{\frac{L}{3g}}{\displaystyle \underset{{\theta }_0}{\overset{\pi /2}{\int }}\frac{d\theta }{\sqrt{\cos {\theta }_0-\cos \theta }}}}$

Empleando la fórmula del coseno del ángulo doble cos2A=cos²A-sin²A y la relación sen²A+cos²A=1

${\displaystyle P_v=\sqrt{\frac{L}{6g}}{\displaystyle \underset{{\theta }_0}{\overset{\pi /2}{\int }}\frac{d\theta }{\sqrt{{\cos }^2\left(\frac{{\theta }_0}{2}\right)-{\cos }^2\left(\frac{\theta }{2}\right)}}}}$

Haciendo el cambio de variable

${\displaystyle \begin{array}{l}\text{sin}\phi =\frac{\cos \left(\frac{\theta }{2}\right)}{k}k=\cos \left(\frac{{\theta }_0}{2}\right)\\ d\theta =\frac{-2k\cos \phi ·d\phi }{\text{sin}\left(\frac{\theta }{2}\right)}=\frac{-2k\cos \phi ·d\phi }{\sqrt{1-k^2{\text{sin}}^2\phi }}\end{array}}$

Llegamos finalmente, a la expresión deseada para el tiempo P_v que tarda la varilla en llegar al suelo cuando se suelta en la posición angular θ₀. Una expresión similar a la obtenida para el periodo de un péndulo para cualquier amplitud.

${\displaystyle P_v=\sqrt{\frac{2L}{3g}}{\displaystyle \underset{{\phi }_0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-k^2{\text{sin}}^2\phi }}}\text{sin}{\phi }_0=\frac{1}{\sqrt{2}k}}$

La integral se puede calcular numéricamente o se puede encontrar en tablas, si la escribimos como diferencia entre la integral elíptica completa cuyos límites son 0 y π/2 y la integral elíptica de primera especie de límites 0 a φ₀.

${\displaystyle P_v=\sqrt{\frac{2L}{3g}}\left({\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-k^2{\text{sin}}^2\phi }}}-{\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}\frac{d\phi }{\sqrt{1-k^2{\text{sin}}^2\phi }}}\right)\text{sin}{\phi }_0=\frac{1}{\sqrt{2}k}}$

El código MATLAB calcula la diferencia entre las dos integrales elípticas, cuando introducimos la posición inicial θ₀ de la varilla en grados.

angulo=10;  %ángulo en grados
L=2; %longitud de la varilla
k=cos(angulo*pi/360);
phi=asin(1/(sqrt(2)*k));
t=(ellipke(k^2)-ellipticF(phi,k^2))*sqrt(2*L/(3*9.8));
fprintf('El tiempo de caída es %1.4f\n',t);

El tiempo de caída es 1.0866

Comparación de los dos movimientos

Comparación de aceleraciones

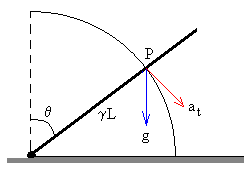
Comparamos la aceleración de la partícula cuando se encuentra en la posición P a una distancia γL del eje de rotación, con la aceleración inicial del punto P de la varilla. En la figura se muestran ambas aceleraciones

El punto P de la varilla describe una circunferencia de radio γL. Hallamos su aceleración tangencial a_t.

${\displaystyle a_t=\gamma L\alpha =\frac{3g}{2}\gamma ·\text{sin}\theta }$

La aceleración de la gravedad en dicha dirección es g·sinθ

Si la primera es mayor que la segunda, se cumplirá que la varilla cae más deprisa que la partícula.

${\displaystyle \frac{3g}{2}\gamma ·\text{sin}\theta >g·\text{sin}\theta \gamma >\frac{2}{3}}$

Como vamos a comprobar, esta es una condición necesaria pero no suficiente para que la varilla llegue antes al suelo que la partícula.

Comparación de tiempos de vuelo

Comparemos los tiempos que requiere cada cuerpo para alcanzar el suelo

La partícula sale de la posición y₀=γLcosθ₀ y llega al suelo en el instante P_p

${\displaystyle P_p=\sqrt{\frac{2\gamma L\text{cos}{\theta }_0}{g}}}$

La varilla parte de la posición angular inicial θ₀ y tarda un tiempo P_v

${\displaystyle P_v=\sqrt{\frac{2L}{3g}}{I}_e}$

Donde I_e es la diferencia entre los valores de las dos integrales elípticas de primera especie del apartado anterior.

La varilla llegará antes que la partícula si se cumple  que P_p>P_v, o bien

${\displaystyle \gamma <\frac{I_e^2}{3\cos {\theta }_0}}$

La posición inicial de la partícula γL depende de la posición angular inicial de la varilla θ₀, para que la varilla llegue antes que la partícula. En la siguiente tabla:

• La primera columna, es la posición angular inicial θ₀

• La segunda, I_e es la diferencia de las dos integrales elípticas

• La tercera, es el cociente ${\gamma }_c=\frac{I_e^2}{3\cos {\theta }_0}$

Los números en las columnas de la tabla nos sugieren las siguientes conclusiones:

Para cada posición angular inicial θ₀, se tiene que

• si γ< γ_c la partícula llega antes al suelo que la varilla

• si γ>γ_c la varilla llega antes al suelo que la partícula

Como γ es menor que la unidad, para las posiciones angulares θ₀=30º, 40º, la partícula siempre llega antes que la varilla. Como podemos comprobar, mediante el programa interactivo, el ángulo mínimo para el cual γ_c=1 es θ₀≈42º

Para un valor dado γ<0.666…=2/3, la varilla llegará al suelo después de la partícula cualquiera que sea el ángulo inicial θ₀ de partida tal como puede apreciarse en la tabla.

Actividades

Se introduce

• La posición angular inicial θ₀, (en grados) que forma la varilla con la dirección vertical, en el control titulado Ángulo
• La posición inicial de la partícula γL siendo γ≤1, en el control titulado Posición .
• La longitud de la varilla se ha fijado en L=2 m
• La masa de la varilla y de la partícula se ha fijado en m=1 kg.

Se pulsa en el botón titulado Nuevo

Se observa el movimiento de rotación de la varilla y el movimiento de la partícula. Investigar para que posiciones y ángulos de partida la varilla llega al suelo antes que la partícula.

Fuerzas F_x y F_y que se ejercen sobre la varilla en su eje de rotación.

El centro de masas de la varilla describe un movimiento circular de radio L/2. Por tanto, la aceleración del c.m. tiene dos componentes:

• la aceleración tangencial
• la aceleración normal

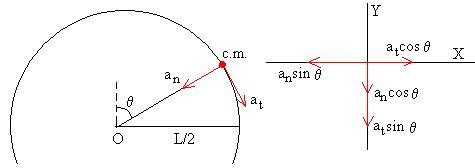
En la parte izquierda de la figura, se muestra las direcciones de la aceleración tangencial y normal cuando la varilla hace un ángulo θ con la vertical. En la parte derecha de la figura, se muestra las componentes rectangulares de dichas aceleraciones.

Aplicando la segunda ley de Newton escribimos

m(a_t·cosθ-a_n·sinθ)=F_x
m(a_n·cosθ+a_t·sinθ)=mg-F_y

${\displaystyle \begin{array}{l}{a}_t=\alpha \frac{L}{2}=\frac{3g}{4}\text{sin}\theta \\ a_n={\omega }^2\frac{L}{2}=\frac{3}{2}g(\text{cos}{\theta }_0-\text{cos}\theta )\end{array}}$

Dado el ángulo θ, despejamos F_x y F_y del sistema de ecuaciones.

${\displaystyle \begin{array}{l}{F}_x=\frac{3mg}{4}\text{sin}\theta (3\text{cos}\theta -2\text{cos}{\theta }_0)\\ F_y=mg-\frac{3mg}{4}(1+2\text{cos}\theta \text{cos}{\theta }_0-3{\text{cos}}^{\text{2}}\theta )\end{array}}$

Cuando la varilla parte de una posición casi vertical, θ₀≈0, la conponente vertical vale, aproximadamente

${\displaystyle F_y\approx mg\left(\frac{1}{4}-\frac{3}{2}\cos \theta +\frac{9}{4}{\cos }^2\theta \right)=\frac{mg}{4}{\left(3\cos \theta -1\right)}^2}$

Se anula para el ángulo tal que cosθ=1/3, θ=70.5°

La componente horizontal vale, aproximadamente, $F_x=\frac{\sqrt{2}}{2}mg$

Ejemplo:

• Si la varilla tiene una masa m=1 kg
• y el ángulo inicial es θ₀=45º

Calcular F_x y F_y cuando θ=60º

Primero calculamos las componentes de la aceleración

a_t=6.37 m/s²
a_n=3.04 m/s²

Luego, calculamos las componentes de la fuerza que se ejerce sobre la varilla en el eje

F_x=0.546 N
F_y=2.765 N

Fuerzas y momento internos

En Internet encontramos vídeos que muestra la caída de una chimenea y observamos que se rompe a una cierta altura antes de llegar al suelo. Para predecir la altura es necesario conocer las fuerzas y momento internos.

Una chimenea es una estructura hecha de ladrillo o cemento de sección variable que no es fácil de analizar. En esta sección, nos limitaremos a calcular las fuerzas internas P_r y P_θ y el momento N_b que se ejercen sobre la porción r inferior de una varilla homogénea que cae desde la posición vertical

Cuando la varilla de masa m y longitud L, forma un ángulo θ con la dirección vertical, las fuerzas que actúan sobre la varilla son:

• El peso, mg
• la fuerza F, en el eje de rotación O

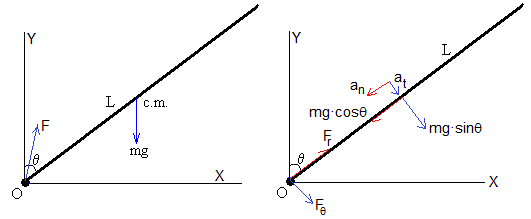
El centro de masas describe un movimiento circular de radio L/2.

• La ecuación del movimiento en la dirección tangencial es

${\displaystyle m\frac{L}{2}\frac{d^2\theta }{d{t}^2}=mg\sin \theta +F_{\theta }}$

• La ecuación del movimiento en la dirección radial es

${\displaystyle -m{\left(\frac{d\theta }{dt}\right)}^2\frac{L}{2}=-mg\cos \theta +F_r}$

• La ecuación del movimiento de rotación alrededor del eje perpendicular a la varilla y que pasa por O es

${\displaystyle \left(\frac{1}{3}m{L}^2\right)\frac{d^2\theta }{d{t}^2}=\frac{L}{2}mg\sin \theta }$

La última ecuación nos proporciona la aceleración angular

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{3}{2}\frac{g}{L}\sin \theta }$

Integramos esta ecuación diferencial, sabiendo que la velocidad angular w=dθ/dt=0 para θ=0, parte del reposo en la posición vertical

${\displaystyle \begin{array}{l}\frac{d^2\theta }{d{t}^2}=\frac{d\omega }{dt}=\frac{d\omega }{d\theta }\frac{d\theta }{dt}=\omega \frac{d\omega }{d\theta }\\ \frac{1}{2}\frac{d{\omega }^2}{d\theta }=\frac{3}{2}\frac{g}{L}\sin \theta \\ {\omega }^2-0=3\frac{g}{L}{\displaystyle \underset{0}{\overset{\theta }{\int }}\sin \theta ·d\theta }\\ {\left(\frac{d\theta }{dt}\right)}^2=3\frac{g}{L}\left(1-\cos \theta \right)\end{array}}$

Alternativamente, aplicamos el principio de conservación de la energía al movimiento de rotación

${\displaystyle \begin{array}{l}mg\frac{L}{2}=\frac{1}{2}\left(\frac{1}{3}m{L}^2\right){\left(\frac{d\theta }{dt}\right)}^2+mg\frac{L}{2}\cos \theta \\ {\left(\frac{d\theta }{dt}\right)}^2=3\frac{g}{L}\left(1-\cos \theta \right)\end{array}}$

Despejamos las componentes de la fuerza que ejerce el eje de rotación sobre la varilla.

${\displaystyle \begin{array}{l}{F}_{\theta }=-\frac{1}{4}mg\sin \theta \\ F_r=\frac{5}{2}mg\left(\cos \theta -\frac{3}{5}\right)\end{array}}$

Fuerzas y momento interno

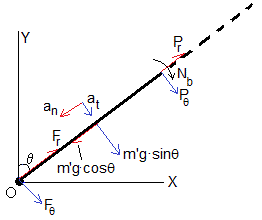
Vamos a estudiar el movimiento de una porción de varilla de longitud r y de masa m'=mr/L, el centro de masas está situado a r/2 del eje O

Las fuerzas que actúan sobre esta porción de varilla son externas e internas (que ejerce la porción L-r de varilla)

• El peso, m'g=mg(r/Lr)
• la fuerza que ejerce el eje de rotación, F, calculada en el apartado anteior
• la fuerza P que ejerce la porción (L-r) de varilla
• El momento N_b, que ejerce dicha porción de varilla

El centro de masas de la porción de varilla describe un movimiento circular de radio r/2.

• La ecuación del movimiento en la dirección tangencial

${\displaystyle \left(m\frac{r}{L}\right)\frac{r}{2}\frac{d^2\theta }{d{t}^2}=\left(m\frac{r}{L}\right)g\sin \theta +F_{\theta }+P_{\theta }}$

• La ecuación del movimiento en la dirección radial

${\displaystyle -\left(m\frac{r}{L}\right){\left(\frac{d\theta }{dt}\right)}^2\frac{r}{2}=-\left(m\frac{r}{L}\right)g\cos \theta +F_r+P_r}$

• La ecuación del movimiento de rotación alrededor del eje perpendicular a la varilla y que pasa por O es

${\displaystyle \left(\frac{1}{3}\left(m\frac{r}{L}\right)r^2\right)\frac{d^2\theta }{d{t}^2}=\frac{r}{2}\left(m\frac{r}{L}\right)g\sin \theta +N_b+P_{\theta }r}$

Conocemos la velocidad y la aceleración angular de la varilla y las componentes de la fuerza en el eje de rotación, despejamos las fuerzas internas P_r, P_θ y el momento N_b

${\displaystyle \begin{array}{l}{P}_{\theta }=\frac{3}{4}mg\sin \theta \left(\frac{r^2}{L^2}-\frac{4}{3}\frac{r}{L}+\frac{1}{3}\right)\\ P_r=-\frac{1}{2}mg\left(1-\frac{r}{L}\right)\left(\left(5+3\frac{r}{L}\right)\cos \theta -3\left(1+\frac{r}{L}\right)\right)\\ N_b=-\frac{1}{4}mgr{\left(1-\frac{r}{L}\right)}^2\sin \theta \end{array}}$

Comprobamos que N_b y P_θ están relacionados

${\displaystyle P_{\theta }=-\frac{\partial N_b}{\partial r}}$

• Componenente P_r de la fuerza

hold on
for th=(0:15:90)*pi/180
    f=@(x) -(1-x).*((5+3*x)*cos(th)-3*(1+x))/2;
    fplot(f,[0,1],'displayName',num2str(th*180/pi))
end
hold off
xlabel('r/L')
ylabel('P_r/(mg)')
legend('-DynamicLegend','location','best')
grid on
title('Fuerza P_r')



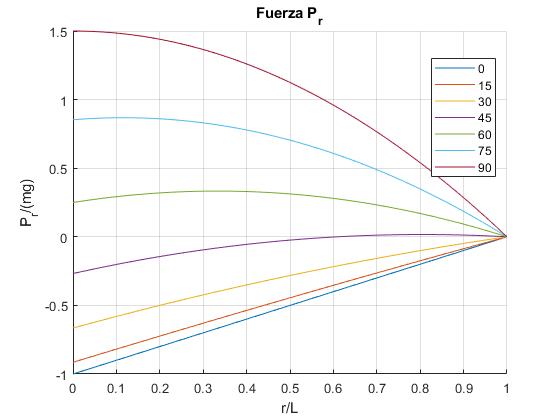
P_r es negativo para ángulos pequeños θ, se hace positivo a partir de θ=45°. El signo negativo indica una fuerza de compresión debido al peso de la parte (L-r) de la varilla

• Componenente P_θ de la fuerza

hold on
for th=(0:15:90)*pi/180
    f=@(x) 3*sin(th)*(x.^2-4*x/3+1/3)/4;
    fplot(f,[0,1],'displayName',num2str(th*180/pi))
end
hold off
xlabel('r/L')
ylabel('P_\theta/(mg)')
legend('-DynamicLegend','location','best')
grid on
title('Fuerza P_\theta')



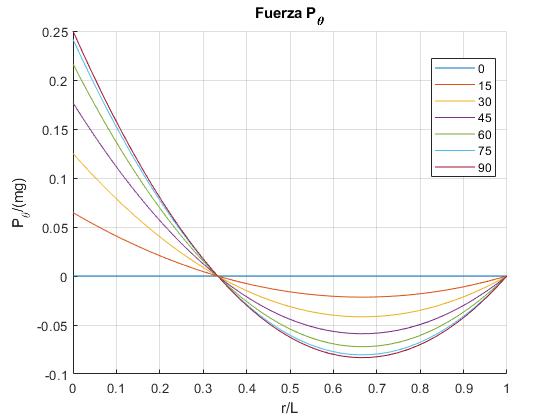
P_θ es grande para r/L=0 (en la base), se hace nulo para r/L=1/3, y mínimo para r/L=2/3, como puede comprobarse derivando P_θ con respecto de x=r/L e igualando a cero.

y=x²-4x/3+1/3,
dy/dx=2x-4/3=0, x=2/3

• Momento N_b

hold on
for th=(0:15:90)*pi/180
    f=@(x) -x.*(1-x).^2*sin(th)/4;
    fplot(f,[0,1],'displayName',num2str(th*180/pi))
end
hold off
xlabel('r/L')
ylabel('N_b/(mgL)')
legend('-DynamicLegend','location','best')
grid on
title('Momento N_b')



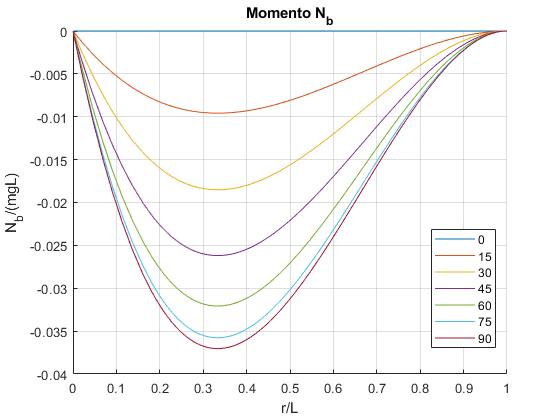
N_b es siempre negativo, lo que indica que tiene sentido opuesto (sentido contrario a las agujas del reloj) a la supuesto inicialmente. N_b es nulo en la parte superior de la varilla r/L=1 y en la parte inferior r/L=0, y presenta un mínimo para r/L=1/3, como puede comprobarse derivando N_b con respecto de x=r/L e igualando a cero

y=x(1-x)²
dy/dx=3x²-4x+1=0, x=1/3

Las posiciones importantes de la varilla son r/L=1/3 y 2/3 medidas desde el eje de rotación

Referencias

Para el apartado "Tiempo que tarda la varilla en caer al suelo"

Theron W. The "faster than gravity" demostration revisited. Am. J. Phys. 56 (8) August 1988, pp. 736-739

Peter F Hinrichsen. The physics of falling chimney stacks. Phys. Educ. 56 (2021) 055023

Gabriele Varieschi, Kaoru Kamiya. Toy models for the falling chimney. Am. J. Phys. 71 (10), October 2003, pp. 1025-1031