Una caja que puede volcar

De nuevo tenemos un ejemplo de aplicación del principio de conservación del momento angular. El sistema formado por el bloque y el obstáculo puntual O no es aislado. Sin embargo, la fuerza exterior que actúa en O tiene un momento nulo, por lo que el momento angular respecto de O es constante.

$\vec{M_{e x t}} = \frac{d \vec{L}}{d t} \vec{M_{e x t}} = 0 \vec{L} = cte$

Momento angular antes del choque

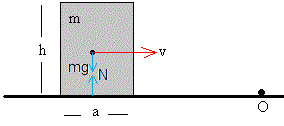
Es el momento angular del bloque respecto de O es equivalente al momento angular de una partícula de masa m situada en el centro de masas del bloque y que se mueve con velocidad v.

$\vec{L} = \vec{r} \times m \vec{v}$ . El módulo del momento angular es L=mv·h/2

El momento total de las fuerzas externas: peso mg y reacción del plano horizontal N, respecto de O, es nulo

Momento angular después del choque

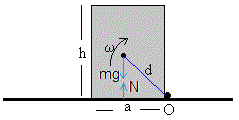
El momento de inercia de un bloque rectangular de masa m y de dimensiones a y h respecto de un eje perpendicular al plano del rectángulo y que pasa por su centro.

$I_{c} = m \frac{a^{2} + h^{2}}{12}$

La dimensión del bloque perpendicular al plano del rectángulo considerado no interviene en el problema

Para calcular el momento de inercia respecto de un eje paralelo al anterior y que pase por el vértice O aplicamos el teorema de Steiner I_O=I_c+md²

$I_{O} = m \frac{a^{2} + h^{2}}{3}$

El momento angular de este sólido rígido que gira alrededor de un eje perpendicular al plano del rectángulo y que pasa por O es

L=I₀·ω

Principio de conservación del momento angular

Aplicando el principio de conservación del momento angular, despejamos la velocidad angular ω del bloque rectangular, justamente después del choque.

$ω = \frac{m v h}{2 \cdot I_{0}}$

Balance energético

Energía perdida en la colisión

La energía antes del choque, es la energía cinética de traslación del bloque $\frac{1}{2} m v^{2}$
La energía después del choque, es la energía cinética de rotación del bloque alrededor del eje que pasa por O, $\frac{1}{2} I_{0} ω^{2}$

La energía perdida en la colisión es la diferencia entre estas dos energías. En la parte superior del programa interactivo, observamos que la mayor parte de la energía cinética inicial del bloque se pierde en la colisión con el obstáculo puntual O y solamente, una pequeña parte de la energía inicial se convierte en energía cinética de rotación del bloque después del choque

Movimiento después del choque

Ecuación de la dinámica de rotación

Después del choque tenemos un sólido rígido en rotación alrededor de un eje fijo que pasa por O. La ecuación de la dinámica de rotación es M=I₀·α

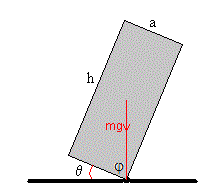
M es el momento del peso que actúa en el centro de masa del bloque, (véase una figura un poco más abajo)

mgd·cos(θ +φ )

donde φ es el ángulo que forma la diagonal con la base del rectángulo tanφ =h/a, y θ es el ángulo que se levanta la base del rectángulo, véase la figura más abajo.

La ecuación de la dinámica de rotación se escribe

-mgd·cos(θ+ φ)=I₀·α

como la aceleración angular no es constante, obtenemos la posición angular θ en función del tiempo, resolviendo la ecuación diferencial de segundo orden por procedimientos numéricos

$\frac{d^{2} θ}{d t^{2}} + \frac{m g d}{I_{0}} \cos (θ + φ) = 0$

Con las siguientes condiciones iniciales: en el intante t=0, θ=0, dθ/dt=ω, velocidad angular después del choque.

Principio de conservación de la energía

Sin embargo, es mucho más fácil aplicar el principio de conservación de la energía para obtener información sobre el comportamiento del sólido en rotación.

En la figura de la derecha, el punto rojo inferior representa la posición del c.m. en el instante inicial θ =0, y el punto rojo superior representa la posición del c.m. cuando la base de la caja ha girado un ángulo θ. La diferencia de alturas entre la posición inicial y final del c.m. es h.

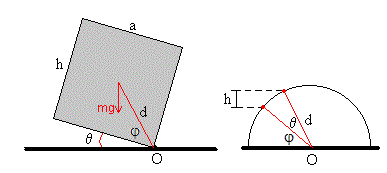
Calculamos el ángulo máximo θ que se levanta la base inferior por encima del suelo.

La energía cinética después del choque se convierte en energía potencial

$\frac{1}{2} I_{0} ω^{2} = m g h h = d \sin (θ + φ) - d \sin (φ)$

Puede ocurrir que la velocidad del bloque sea tan grande que el ángulo θ , sobrepase el valor máximo que hace que el centro de masas pase por encima de O. Entonces el bloque cae hacia el otro lado.

Como vemos este ángulo máximo es tal que θ+φ=π/2 ó 90º

Para que esto ocurra, la energía cinética de la caja después del choque tiene que ser mayor que la energía potencial del bloque correspondiente a una altura de su c. m. igual a d.

$\frac{1}{2} I_{0} ω^{2} \geq m g \cdot (d - d \sin φ)$

Cuando la velocidad angular ω no alcanza el valor límite ω_l

$ω_{l} = \sqrt{\frac{2 m g d}{I_{0}} (1 - \sin φ)}$

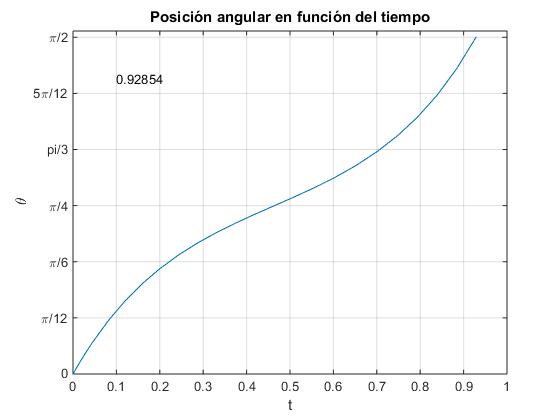
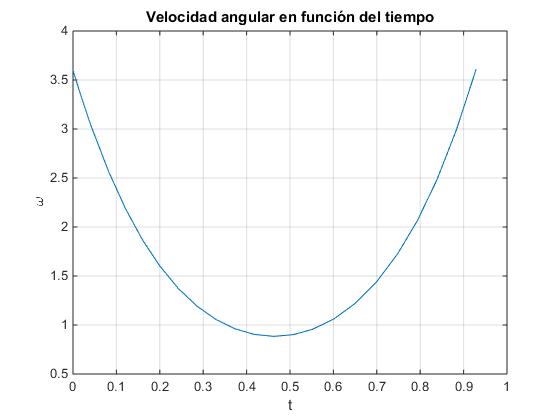
la posición final de la caja es θ=0. Cuando supera el valor límite, la posición final de la caja es θ=π/2. Fijarse que en el primer caso, θ es una función que crece y luego, decrece con el tiempo. En el segundo caso, θ es una función siempre creciente con el tiempo t

m=0.2; %masa del bloque
v=2.4; %velocidad del bloque
h=0.5; %altura del bloque
a=0.5; %anchura del bloque
I0=m*(a^2+h^2)/3; %momento de inercia respecto del vértice O
w0=m*v*h/(2*I0); %velocidad angular después del choque
phi=atan(h/a);
d=sqrt(a^2+h^2)/2; %media diagonal
k=m*9.8*d/I0;
%valor límite de la velocidad angular después del choque
w_lim=sqrt(k*2*(1-sin(phi))); 

x0=zeros(1,2);
x0(1)=0;  %posición de partida
x0(2)=w0;
f=@(t,x) [x(2);-k*cos(x(1)+phi)]; 
tspan=[0 5];
opts=odeset('events',@caja_ode45);
if w0>w_lim
    opts=odeset('events',@caja1_ode45);
end
[t,x,te]=ode45(f,tspan,x0, opts);

plot(t,x(:,1))
set(gca,'YTick',0:pi/12:pi/2)
set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','pi/3',
'5\pi/12','\pi/2'})
text(0.1,max(x(:,1))-0.2,num2str(te)) %tiempo de caída
grid on
xlabel('t')
ylabel('\theta');
title('Posición angular en función del tiempo')
figure
plot(t,x(:,2))
grid on
xlabel('t')
ylabel('\omega');
title('Velocidad angular en función del tiempo')

Definimos dos funciones una para que el proceso de integración se detenga cuando la posición final del bloque sea θ=0, si se cumple que ω<ω_l, en caso contrario, el proceso de integración se detiene cuando θ=π/2

function [detect,stopin,direction]=caja_ode45(t,x)
    detect=x(1); 
    stopin=1;
    direction=-1; 
end

function [detect,stopin,direction]=caja1_ode45(t,x)
    detect=x(1)-pi/2; 
    stopin=1;
    direction=1; 
end

Ejemplos:

Ejemplo 1º:

Masa del bloque, m=0.2 kg
Velocidad del bloque, v=2.2 m/s
Altura del bloque, h=50 cm
Anchura del bloque, a=50 cm

Choque. Principio de conservación del momento angular

Distancia d del c. m. al vértice del rectángulo $d = \sqrt{{0.25}^{2} + {0.25}^{2}} = 0.35 m$
Momento de inercia I₀= 0.033 kgm²

Momento angular inicial L=0.2·2.2·0.25=0.11 kg·m²/s
Momento angular final L=I₀·ω

Conservación del momento angular: ω =3.3 rad/s

Movimiento después del choque. Principio de conservación de la energía

La energía cinética después del choque se transforma en energía potencial, cuando se alcanza el ángulo máximo girado por la base del bloque.

$\frac{1}{2} 0.033 \cdot {(3.3)}^{2} = 0.2 \cdot 9.8 \cdot h h = 0 .093 m$

A partir de la altura h a la que se eleva el centro de masas, obtenemos el ángulo que ha girado el bloque alrededor del eje que pasa por el vértice O.

h=d·sin(θ+φ)-d·sinφ , con φ =45º por ser cuadrada la forma del bloque. Despejamos ángulo θ =30.7º

Ejemplo 2º

Resolviendo el problema en sentido inverso calculamos la velocidad del bloque para que realice un giro completo.

Movimiento después del choque. Principio de conservación de la energía

$\frac{1}{2} I_{0} ω^{2} = m g \cdot (d - d \sin φ)$

con φ =45º por ser cuadrada la forma del bloque

Obtenemos la velocidad angular después del choque, ω =3.49 rad/s

Choque. Principio de conservación del momento angular

m·v·h/2=I₀·ω

Obtenemos la velocidad del bloque v=2.326 m/s.

Introducimos este valor en el control titulado Velocidad inicial y pulsamos el botón titulado Nuevo, observamos que el c.m. de la caja alcanza la posición vertical sin sobrepasarla. Si incrementamos un poquito más la velocidad v se completa el giro.

Actividades

Se introduce

Masa m del bloque (kg), en el control titulado Masa del bloque
Velocidad v del c.m. del bloque (m/s), en el control titulado Velocidad inicial
Altura h (cm), en el control titulado Alto
Longitud de la base a (cm), en el control titulado Ancho

Se pulsa el botón Nuevo

Se observa el movimiento del bloque deslizando por la pista horizontal y su posterior choque con el obstáculo puntual O y el balance energético de la colisión..

Masa del bloque (kg)
Velocidad inicial (m/s)
Altura (cm) Anchura (cm)

Fuerzas sobre la caja en el eje de rotación

Hemos calculado la aceleración angular y la velocidad angular del sistema después del choque, cuando la caja forma un ángulo θ con la vertical tal como se ve en la figura (más abajo).

Ecuación de la dinámica de rotación

I₀α =-mg·d·cos(θ+φ)

Balance energético

$\frac{1}{2} I_{0} ω_{0}^{2} = m g \cdot d (\sin (θ + φ) - \sin φ) + \frac{1}{2} I_{0} ω^{2}$

Siendo ω₀ la velocidad angular de la caja inmediatamente después del choque con el obstáculo O

El centro de masas describe un arco de circunferencia de radio d, por tanto, tiene dos aceleraciones, una tangencial a_t y otra normal a_n.

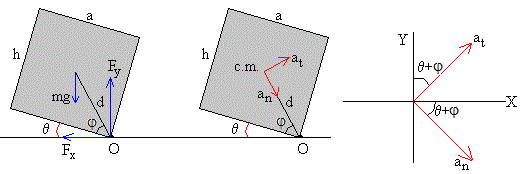
En la figura de la izquierda, dibujamos las fuerzas sobre la caja, en la figura central las aceleraciones. A partir de estos esquemas, planteamos las ecuaciones del movimiento del centro de masas.

m·a_x=-F_x
m·a_y=F_y-mg

Hallamos las componentes a_x y a_y de la aceleración (tercera figura)

a_x=a_t·sin(θ+φ ) +a_n·cos(θ+φ)
a_y=a_t·cos(θ +φ) -a_n·sin(θ+φ)

Teniendo en cuenta que en un movimiento circular

a_t=α·d
a_n=ω²·d

Despejamos F_x y F_y

F_x=-m·d·(α·sin(θ+φ) +ω²·cos(θ+φ))
F_y=m·d·(α·cos(θ+φ) -ω²·sin(θ+φ))+mg

Ejemplo

Volvemos sobre el ejemplo 1º

Masa del bloque, m=0.2 kg
Velocidad del bloque, v=2.2 m/s
Altura del bloque, h=50 cm
Anchura del bloque, a=50 cm

Por ser una caja cuadrada φ =45º, $d = 0.25 \sqrt{2} m$

Momento de inercia I₀= 0.033 kgm²

Choque. Aplicamos el principio de conservación del momento angular para obtener la velocidad angular de la caja inmediatamente después del choque.

ω₀=3.3 rad/s

El enunciado del problema es ahora: calcular los valores de las fuerzas F_x y F_y cuando el ángulo girado por el bloque sea θ =15º.

Calculamos la aceleración angular α, y la velocidad angular ω.

$0.033 \cdot α = - 0.2 \cdot 9.8 \cdot 0.25 \sqrt{2} \cdot \cos (15 º + 45 º) α = - 10 .4 {rad/s}^{2}$

Balance energético

$\frac{1}{2} 0.033 \cdot {3.3}^{2} = 0.2 \cdot 9.8 \cdot 0.25 \sqrt{2} (\sin 60 º - \sin 45 º) + \frac{1}{2} 0 .033· ω^{2} ω = 2.07 rad/s$

Finalmente, calculamos las componentes de la fuerza sobre la caja en el eje O.

$\begin{array}{l} F_{x} = - 0.2 \cdot 0.25 \sqrt{2} (- 10.4 \sin 60 + {2.07}^{2} \cdot \cos 60) = 0.48 N \\ F_{y} = 0.2 \cdot 0.25 \sqrt{2} (- 10.4 \cos 60 - {2.07}^{2} \cdot \sin 60) + 0.2 \cdot 9.8 = 1.33 N \end{array}$